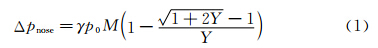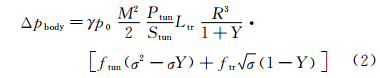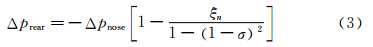0 引 言
当高速列车通过隧道过程中产生压力波，带来了乘客舒适性和列车疲劳强度等问题。在过去的几十年中，各国对高速列车隧道压力波进行了大量的理论和试验研究，研究结果对高速铁路安全运行、乘客舒适性以及隧道设计参数选择等研究提供了正确可靠的依据[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18]。研究隧道压力波的方法有全尺寸现车试验、缩尺模型试验和数值模拟方法，其中，数值模拟方法有一维流动模型[1, 2, 5, 6, 7, 11, 12]和三维流动模型[8, 9, 14, 16, 17]。三维流动模型的数值模拟方法能够揭示压力波的形成过程，给出详细的流场信息,但是对计算机资源要求较高，灵活性较差，不宜进行多方案多工况的研究，对于模拟列车通过长大隧道全过程是无能为力。一维可压缩流动模型在多工况、复杂结构隧道、长大隧道等诸多因素下的压力波计算方面优势明显。一维可压缩流动模型的不足之处在于隧道进口、出口、车头和车尾等三维流动强烈的区域需借助采用压力损失系数建立相应的边界条件[2]。这些区域所涉及的边界条件方程都是非线性方程组，需要采用多次迭代的方法。分析一维流动模型方法，其耗用的计算时间主要在于求解多处边界条件方程中非线性方程组，可以预见对于长大隧道、隧道内附属结构较多、多对列车等情形下的压力波，必然导致在目前计算机水平下，计算时间增多，有的计算工况的计算时间将长达十几个小时。
从可压缩流动理论分析，隧道压力波的物理形成过程是——当列车通过隧道进出洞口端过程中，产生了压缩波或膨胀波，在洞内传播并又经洞口端反射与列车端部反射和折射，再次产生新的膨胀波或压缩波，这些波在隧道内叠加形成压力波。根据压力波的形成机理，Mame William-Louis提出了基于经验计算特征波的简单隧道内压力波计算方法[19]。此方法采用了可压缩流体力学理论为基础得出的特征波计算式，避免了一维可压缩流动模型数值计算求解复杂方程的过程，计算时间极短，能够更加快速得出隧道内和列车外的压力波特性。但是，文献[19]对具体计算方法叙述较少，也没有对所提方法适用性进行分析。本文根据文献[19]所发展的计算方法和国外典型的实车试验结果，建立了高速列车单车通过隧道产生的压力波计算方法，同时与实车试验结果进行比较，并进行了阻塞比、列车速度和隧道长度的参数研究，分析了该方法的适用性，为今后进一步拓展该方法的应用范围和改进提供了基础。 1 隧道压力波的形成与特征波系
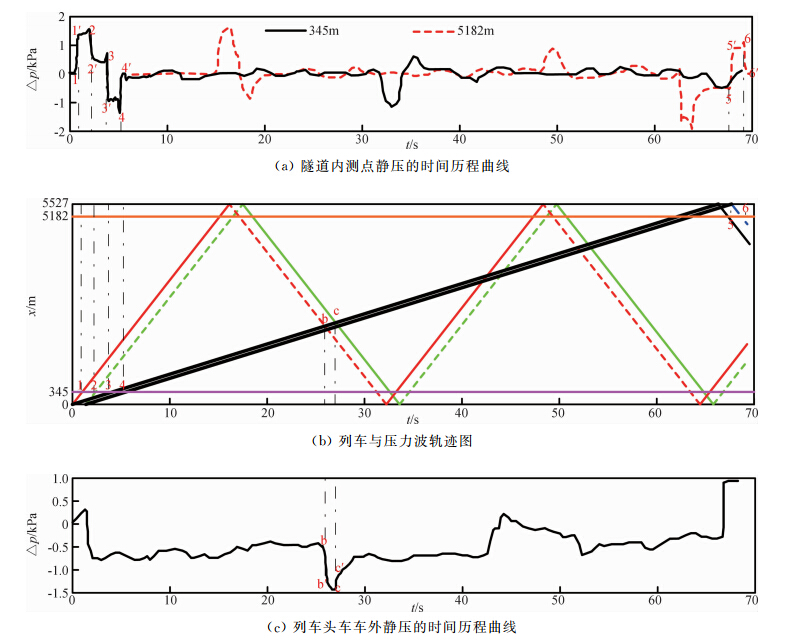
图 1给出了德国高速列车ICE/V通过Mühlberg隧道 时的列车运行轨迹和压力波时间历程曲线的关系图[3]。列车长为114 m、速度为305 km/h，隧道长度为5527 m，其余参数可详见文献[3]。在图 1(b)中，两条黑实线分别表示车头和车尾运动轨迹线，绿、红、蓝色实线表示压缩波的传播轨迹，绿、红、蓝色虚线表示膨胀波的传播轨迹。图 1(a)表示了距隧道进口端345 m和5182 m处静压的时间历程曲线。图 1(c)表示了列车头车车外静压的时间历程曲线。
如图 1所示，当列车车头驶入隧道瞬间，隧道壁 面限制了空气侧向流动和向上流动的空间，使列车所排开的空气受到压缩，导致列车车头前空气压力突然升高，形成快速上升的压缩波Δpnose。其后跟随着列车持续进入隧道产生了近似线性递增的Δpbody，其是由于列车驶入隧道过程中，列车与隧道形成的环状空间长度持续增长，这样使得环状空间中动车组壁面、隧道壁面作用于空气的摩擦力增加。当列车尾部端进入隧道后，车后的流动空间突然扩大，使得车后的压力小于洞外大气压，产生了新的压力下降Δprear，形成了膨胀波。本文将这三个波(即Δpnose、Δpbody、Δprear)构成的波系称之为“列车驶入波”。
 |
| 图 1 单车压力波的形成过程Fig. 1 Pressure wave propagation and associated wave diagram for single train |
在列车驶入过程中，列车驶入波以声速的速度在隧道内传播。它经过距隧道入口345 m时的波形就是1和2之间的压力波形。即该测点压力作用由Δp11′、Δp1′2和Δp22′构成(见图 1(a))。当列车驶入波传播到隧道出口时，其大部分会以属性相反形式的波反射回，其大小可通过其作用在列车bc之间的压力波的大小来确定，即由Δpbb′、Δpb′c和Δpcc′(见图 1(c))。列车驶入波在不断地传播中，由于受到壁面摩擦的影响，其强度会减小。类似于列车驶入，在列车驶出隧道时也会产生一个类似列车驶入波的“列车驶出波”，与列车驶入波的相当相似(见图 1(a)由Δp55′、Δp5′6和Δp66′组成的波系)。另一个问题就是列车周围的压力变化必须被考虑。从图 1(a)可见，在列车头部、车身以及尾部通过距隧道入口345 m处时引起的压力变化分别为Δp33′、Δp3′4和Δp44′。这些波形与列车驶入波类似，就是符号恰好相反。这里把Δp33′、Δp3′4和Δp44′构成的波系称之为“列车行驶波”，该波跟随列车一起运动影响隧道内压力的变化。
这样就由列车驶入波、列车驶出波以及列车行驶波共同组成了列车通过隧道时产生的隧道压力波的特征波系，并认为隧道压力波是由这些波系以及其反射波叠加而成。 2 特征波计算说明
基于一维准定常不可压缩模型，建立了列车前方压缩波前后流动空气连续性方程、动量方程和能量方程，以及建立了列车车头前后流动空气的连续性方程、能量方程和压力损失方程。联立这六个方程，并考虑密度为常数，可得出由列车驶入隧道产生的初始压缩波的压力突升最大值Δpnose的计算公式，具体见下式[7]：
式中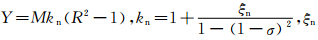
为车头压力损失系数，
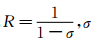为阻塞比，M为列车马赫数，γ为空气比热比。
再考虑到时间关系，可把初始压缩波波形定义为Δpnosef(t)。f(t)为初始压缩波波形的时间函数。
列车车身驶入过程中，由于车壁和隧道壁面摩擦力的作用，使得车前压力继续上升。根据流体壁面摩擦计算公式[2]，并引入推导Δpnose中得出的列车环形空间的空气流速的结果，可推出下式来计算这里压力升值：
式中Ptun为隧道周长，Stun为隧道截面积，Ltr为列车长度，ftun为隧道壁面摩擦系数，ftr为列车壁面摩擦系数。
对于列车车尾驶入造成的压力下降，目前由于车尾环形空间流动的复杂性而没有有效的理论近似方法。但是特征线法的计算结果表明，如果不关注下降波的时间梯度以及车头车尾外形一致的前提下，其大小可以通过下式来确定[19]：
使用式(1)～式(3)，可以计算出列车驶入波。再由列车行驶波和列车驶入波大小相等而符号相反的结论，列车行驶波也可由式(1)～式(3)确定。再者根据列车驶出波与列车驶入波相当相似的结论，也可确定出列车驶出波的大小。这样隧道压力波的特征波就可以被确定。因为列车驶入波是始于列车车头驶入隧道瞬间，终于车尾进入隧道瞬间，并是以声速传播的，所以其长度为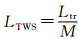
。而列车行驶波是随列车车体一起移动，所以其长度与列车车长相同(见图 2)。
 |
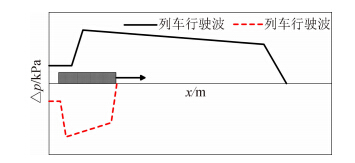| 图 2 隧道内的特征波Fig. 2 Characteristic waves in the tunnel |
采用压力特征波系计算隧道内以及列车上观测点的压力值的方法，就是把传播到观测点的特征波的值相加。计算中，还有两个问题需要注意：一是压力波在隧道端口反射时的反射系数的确定，可通过试验的方法来确定；二是压力波在隧道内传播的衰减问题。
隧道空间和环形空间压力衰减可由下式来确定：
式中α可从试验中得出[17]，对于碎石道床α=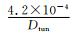
；对于板式道床
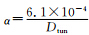。式中Dtun为隧道等效直径。
3 计算方法说明这里以隧道内某测点压力计算为例说明特征波叠加法。如图 3所示，隧道内测点(该测点距隧道入口的距离为Lc)与时刻6.5 s交点为d。在0～6.5 s之间隧道该点共受到三个波系的影响：列车驶入波(黑色细线)及其反射波(蓝色虚细线)和列车驶出波(红色虚细线)的影响。
 |
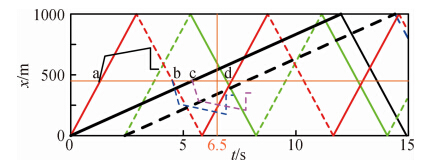| 图 3 隧道内的特征波叠加示意图Fig. 3 Schematic view of characteristic waves superposition in the tunnel |
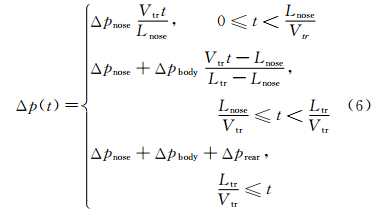
按照第2节提到的特征波的计算方法，且认为初始压缩波大小与列车头部进入隧道的长度成正比关系，即f(t)=Vtr/Lnose，这样列车驶入波可以用下式完整的表示：
依据第2节的分析结果可以确定出列车驶出波 Δp(t)=ΔpTNS(t)，列车行驶波ΔpTNS(t)=－ΔpTWS(t)。
这样再考虑摩擦和洞口反射后在0～6.5 s之间作用于隧道测点三个压力波系就可以分别用下面三个式子来表示：
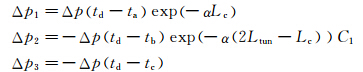
而在6.5 s隧道内测点的压力就是这三个压力波的之和，即Δp=Δp1+Δp2+Δp3。用同样的方法该测点其它时刻的压力值。对于列车车外测点压力计算可转换为某一时刻列车测点所对应可隧道内测点的压力计算。 4 计算结果验证及分析 4.1 与试验结果的比较
这里，采用文献[20]的现车试验数据进行对比。试验的列车车速约295 km/h。图 4和图 5分别给出了文献试验结果和本文方法以及特征线法(Method of Characteristics，MOC)的计算结果。从图 4和图 5可见：本文方法计算结果能较好反映试验数据的结果，说明本方法是合理的；同时本课题组所开发特征线法的计算结果也与试验数据吻合，这样也同时证明了MOC方法的正确性。目前大量的工作结果也说明采用MOC进行高速列车隧道压力波具有合理性[6, 18]。随后的研究工作中用MOC的计算结果作为对比数据。
 |
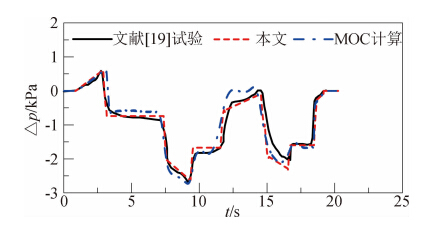| 图 4 距列车车头72 m处车外压力时间历程曲线Fig. 4 Static pressure excursion at 72 m from train nose |
 |
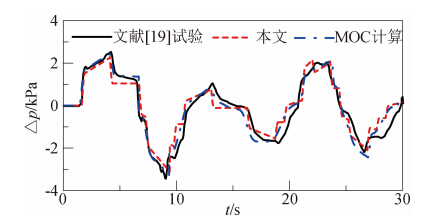| 图 5 距隧道入口550 m处隧道内静压的时间历程曲线Fig. 5 Static pressure excursion at 550 m from entry portal |
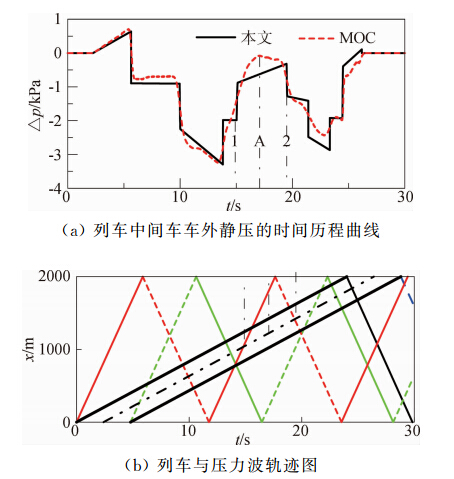
图 6给出车速为300 km/h、列车与隧道长度分别为400 m和2000 m不同阻塞比情形下列车中间车车外静压的时间历程曲线。其中列车横截面积为12.3 m2。
 |
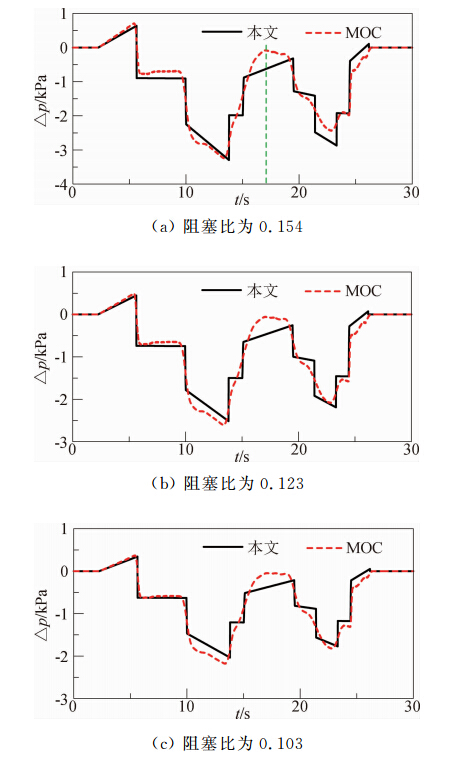| 图 6 不同阻塞比时列车中间车车外静压的时间历程曲线Fig. 6 Static pressure excursion on the middle coach of train with the different blockage ratios |
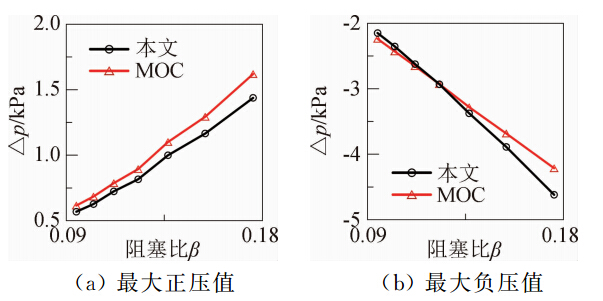
对比图 6中本文方法和MOC计算结果可以发现：两种结果波形和峰值基本相符，但在A时刻差异还是比较明显。对于这一差异，可结合图 7来分析。从图 7看出本文计算结果符合压力波的作用规律，即在1时刻受到压缩波的作用突然上升，在2时刻受到膨胀波的作用明显下降。之所以与MOC在A时刻差异明显，是由于本文计算方法未考虑气流流动带来的影响。 图 8给出了不同阻塞比下MOC和本文基于特征波系计算所得的车外最大压力的对比图。从图 6和图 8中可以发现：随着阻塞比的增大，MOC和本文的计算结果差异增大。分析原因是式(2)得出是基于车头附近流场是不可压缩的这样一个假设，但实际上随着阻塞比的增大(也就是隧道净空面积的减少)，车前的空气的压缩效应很明显，这样如果继续按不可压缩处理就会带来比较大的误差。虽然这样处理有一定的不合理性，但在阻塞比从0.095变为0.176时本文方法和MOC两种计算结果差异最大也不超过10%。
 |
| 图 7 压力波的形成过程Fig. 7 Pressure wave propagation and associated wave diagram for single train |
 |
| 图 8 车外最大压力与阻塞比的关系曲线Fig. 8 Maximum pressure on the train with the different blockage ratios |
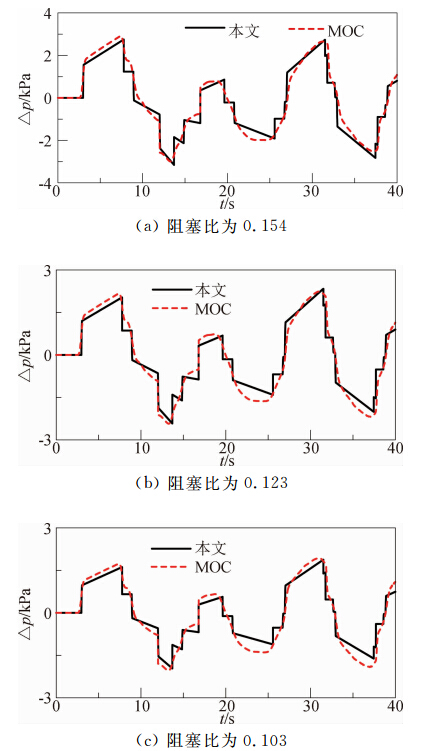
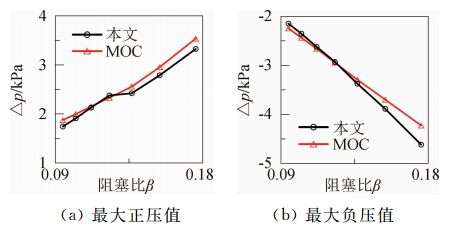
图 9给出车速为300 km/h、列车与隧道长度分别为400 m和2000 m不同阻塞比情形下隧道中央处静压的时间历程曲线。其中列车横截面积为12.3 m2。图 10给出了不同阻塞比下MOC和本文方法计算所得的隧道内最大压力的对比图。从图 9可以看出，本文方 法的曲线也显得比MOC的“有棱有角”。 从图 10可以看出，阻塞比不同时本文方法和MOC计 算出隧道最大正负压值之间差异最大不超过10%。
 |
| 图 9 不同阻塞比时隧道中央处静压的时间历程曲线Fig. 9 Static pressure excursion in tunnel with the different blockage ratios |
 |
| 图 10 隧道内最大压力与阻塞比的关系曲线Fig. 10 Maximum pressure in tunnel with the different blockage ratios |
图 11给出列车与隧道长度分别为400 m和2000 m、阻塞比为0.123、车头损失系数为0.0051、不同车速时列车中间车车外静压的时间历程曲线。图 12给出了列车车外静压的最大值与列车车速之间的关系图。从图 11可以看出，本文计算结果的曲线也显得比MOC的“有棱有角”。从图 12可以看出，随着车速增大本文方法和MOC计算的列车车外最大正压值之间差异增大，而最大负压值的差异基本不变。之所以本文计算出的车外最大正压值误差随着车速增大而增大，同样也是由于本文方法所用关键公式采用不可压缩的假设，而车速的增大使得气流的压缩性增大。
 |
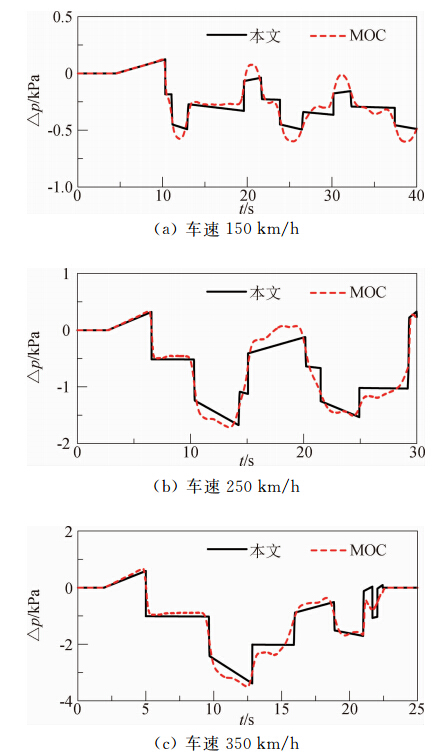| 图 11 不同车速时列车中间车车外静压的时间历程曲线Fig. 11 Static pressure excursion on the middle coach of train with the different train speeds |
 |
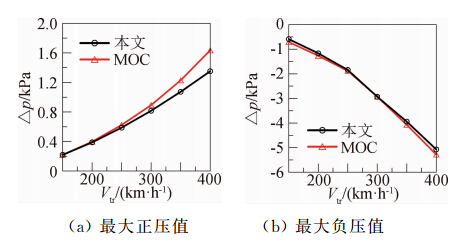| 图 12 车外最大压力与列车速度的关系曲线Fig. 12 Maximum pressure on the train with the different train speeds |
图 13就给出列车与隧道长度分别为400 m和2000 m、阻塞比为0.123、车头损失系数为0.0051、不同车速情形时隧道中央处静压的时间历程曲线。图 14给出了隧道内静压的最大值与列车车速之间的关系图。从图 13和图 14得出的本文结果和MOC时间历程曲线的特征差异以及车速对最大值的影响同图 11和图 12的特点。
 |
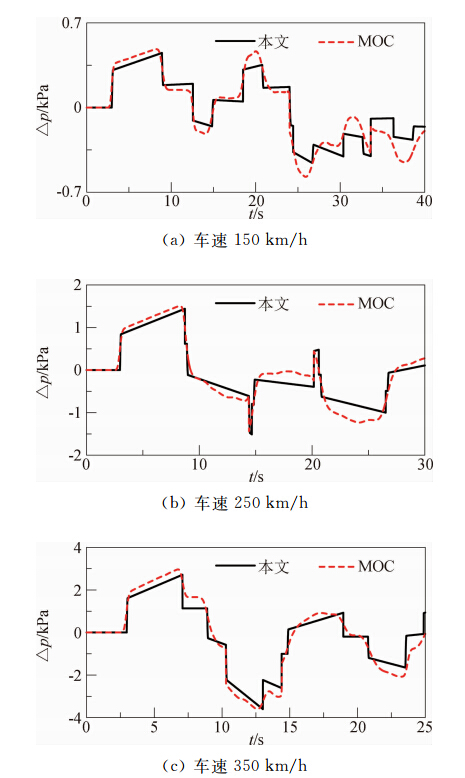| 图 13 不同车速时隧道中央处静压的时间历程曲线Fig. 13 Static pressure excursion in tunnel with the different train speeds |
 |
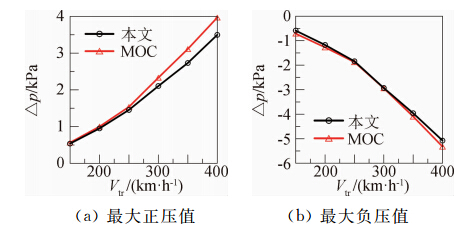| 图 14 隧道内最大压力与列车速度的关系曲线Fig. 14 Maximum pressure in the tunnel with the different train speeds |
这里使用本文方法和MOC分别计算不同隧道长度隧道压力波来验证本文计算方法的正确性。所用参数见表 1。
| 隧 道 | 列 车 | ||
| 横截面积Stun | 100.0 m2 | 截面积Str | 12.3 m2 |
| 周长Ptun | 38.43 m | 周长Ptr | 13.4 m |
| 摩擦系数ftun | 0.005 | 壁面摩擦系数ftr | 0.0028 |
| 入口压力损失系数 | 0.5 | 头部压力损失系数 | 0.0051 |
| 尾部压力损失系数 | 0.02 | ||
| 列车长Ltr | 400 m | ||
| 列车速度Vtr | 300 km/h | ||
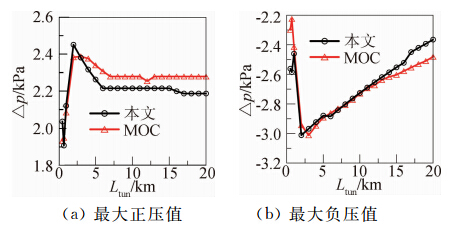
图 15、图 16和图 17分别给出了隧道长度为3000 m、6000 m和12000 m时的隧道内中央处和列车中间车车外压力的时间历程图。图 18和图 19分别给出了列车车外和隧道内静压的最大值与隧道长度之间的关系图。分析这些图可以发现：在常见的隧道范围内，本文方法都是适用的。
 |
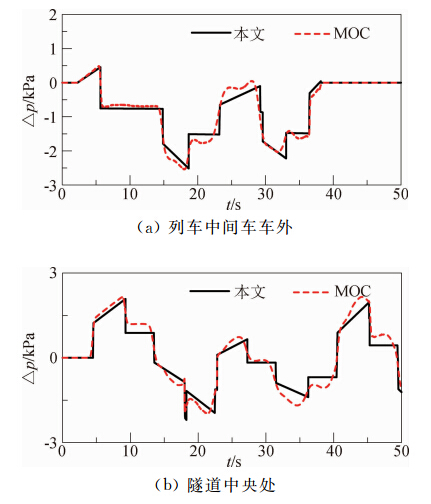| 图 15 列车通过隧道长为3000 m时静压的时间历程曲线Fig. 15 Excursion of static pressure produced by train through 3000 m tunnel |
 |
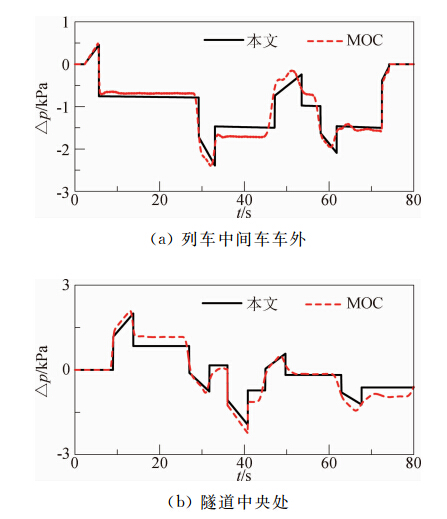| 图 16 列车通过隧道长为6000 m时静压的时间历程曲线Fig. 16 Excursion of static pressure produced by train through 6000 m tunnel |
 |
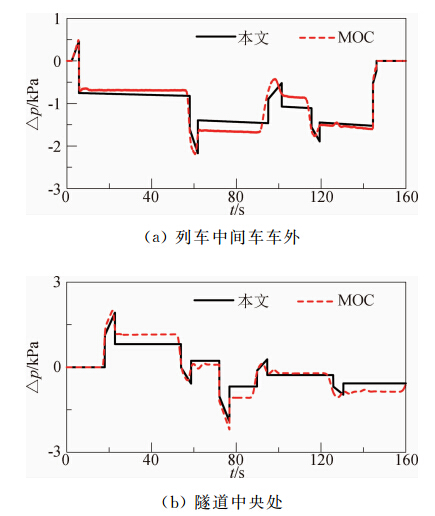| 图 17 列车通过隧道长为12000 m时静压的时间历程曲线Fig. 17 Excursion of static pressure produced by train through 12000 m tunnel |
 |
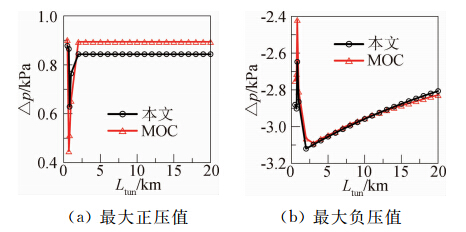| 图 18 列车车外最大压力与隧道长度的关系曲线Fig. 18 Maximum pressure on the train with the different tunnel lengths |
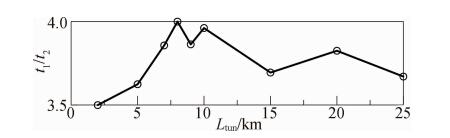
图 20给出了MOC计算时间t1与本文计算方法计算时间t2比值与隧道长度的关系。从图 20中可以归纳出t1/t2的值在3.5～4.0，MOC方法比本文方法计算消耗的时间多。
 |
| 图 19 隧道内最大压力与隧道长度的关系曲线Fig. 19 Maximum pressure in the tunnel with the different tunnel lengths time and the tunnel length |
 |
| 图 20 计算时间比与隧道长度的关系Fig. 20 Relationship between the ratio of computation time and the tunnel length |
本文通过分析列车通过隧道过程中压力波的产生机理，得出了隧道内和列车上任意时刻压力可以看作是多个特征波的叠加的结论，这样把压力波的计算问题就转化为特征波的叠加问题。通过与试验数据和特征线法计算结果的对比，证明了本文所建的叠加法计算压力波方法的正确性和可行性。随后研究了阻塞比、车速和隧道长度的影响特性，验证了本文所建方法具有良好的预测结果。
基于波叠加隧道压力波的计算方法更有利于对压力波机理的认识；避免了采用数值求解的复杂过程，程序编写简单，计算耗时少，有利于进一步分析影响隧道压力波的因素。但是没有考虑到气体流动参数的影响，使得求出的压力波形曲线“有棱有角”，不能用于压力变化率的计算。
| [1] | Woods W A, Pope C W. A generalized flow prediction method for the unsteady flow generated by a train in a single tunnel[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1981, 7: 331-360. |
| [2] | Pope C W, Woods W A. Boundary conditions for the transit of a train through a tunnel with special reference to the the entry and exit mesh fractions and the contact surface[C]//Stephens H S. 4th ISAVVT. Cranfield Bedford England: BHRA, 1982, (C1): 79-105. |
| [3] | Glöckle H. High speed tests with ICE/V passing through tunnels and the effect of sealed coaches on passenger comfort[C]//6th ISAVVT. Durham: BHRA, 1988, (A2): 23-44. |
| [4] | Petes J L. Aerodynamics of very high speed trains and maglev vehicles: state of art and future potential[C]//Dorgham M A. Proceeding of the international association for vehicle design. Channel Islands UK: Inderscience Enterprises Ltd., 1983: 308-341. |
| [5] | Ozawa S. Present situation and future outlook of aerodynamics and aeroacoustic problems of high speed trains[J]. Quarterly Report of RTRI, 1992, 33(1): 33-38. |
| [6] | Mei Yuangui. A study on numerical simulation of high-speed trains induced pressure waves in a single bore tunnel[D]. Chengdu: Southwest Jiaotong University, 1997. 梅元贵. 高速铁路隧道压力波数值模拟研究[D]. 成都: 西南交通大学, 1997. |
| [7] | Woods W A, Pope C W. Experimental study (scale l/70) and numerical simulations on the generation of pressure waves and micro-pressure waves due to high-speed train-tunnel entry[C]//9th ISAVVT. Aosta Valley, Italy, BHR Group, 1997: 877-903. |
| [8] | Aita S, Tabbal A, Mestreau Montmayeur N. CFD aerodynamics of the French high-speed train[C]//International Congress and Exposition. SAE Technical Papers. 1992: 85-99. |
| [9] | Kozo Fujii, Takanobu Ogawa. Aerodynamics of high speed trains passing by each other[J]. Computer & Fluids, 1998, 24(8): 897-908. |
| [10] | Raghunathan R S, Kim H D, Setoguchi T. Aerodynamics of high-speed railway train[J]. Progress in Aerospace Sciences, 2002, 38: 469-514. |
| [11] | Yu Nanyang. A study on numerical simulation and model experiment of the pressure waves of the high-speed trains through tunnels[D]. Chengdu: Southwest Jiaotong University, 1997. 余南阳. 高速铁路隧道压力波数值模拟和模型试验研究[D]. 成都: 西南交通大学, 2004. |
| [12] | Mei Yuangui, Zhou Chaohui, Geng Feng, et al. Numerical method of initial compression waves produced by a high speed train entering a tunnel hood based on one dimensional unsteady compressible flow model[J]. Acta Aerodynamica Sinica, 2006, 24(4): 508-512. 梅元贵, 周朝晖, 耿烽, 等. 高速铁路隧道初始压缩波一维流动模型的数值分析方法[J]. 空气动力学学报, 2006, 24(4): 508-512. |
| [13] | Wang Xiaoyan, Wu Jian. Insitutest and study on the aerodynamic effect of the rolling stock passing through tunnels with a speed of 200 km/h[J]. Modern Tunneling Technology, 2006, 43(1): 43-48. 万晓燕, 吴剑. 时速200 km动车组通过隧道时空气动力学效应现场试验与研究[J]. 现代隧道技术, 2006, 43(1): 43-48. |
| [14] | Mei Yuangui, Zhou Chaohui, Xu Jianlin. Aerodynamics of the high-speed railway tunnel[M]. Beijing: Science Press, 2009. 梅元贵, 周朝晖, 许建林. 高速铁路隧道空气动力学[M]. 北京: 科学出版社, 2009. |
| [15] | Wang Yingxue, Gao Bo, Lu Zhenhua, et al. Aerodynamics effect numeral simulation of high speed train passing through tunnel with mid-station [J]. Acta Aerodynamica Sinica, 2009, 27(3): 369-372. 王英学, 高波, 陆振华, 等. 隧道中部存在车站时列车会车气动效应数值分析[J]. 空气动力学学报, 2009, 27(3): 369-372. |
| [16] | Uystepruyst David, Louis Mame William, Emmanuel Creusé, et al. Efficient 3D numerical prediction of the pressure wave generated by high-speed trains entering tunnels[J]. Computers & Fluids, 2011, 47: 165-177. |
| [17] | Luo Jianjun. The experiment and numerical simulation on the pressure produced by a high-speed train entering into a tunnel[D]. Chengdu: Southwest Jiaotong University, 2003. 骆建军. 高速列车进入隧道产生压缩波的数值模拟及试验研究[D]. 成都: 西南交通大学, 2003. |
| [18] | Wormstall Reitschuster H J, Matschke G, Heine C. Parametrical investigations on aerodynamics effects in tunnels-prediction and validation[C]//10th ISAVVT. Boston USA: BHRA, 2000: 171-183. |
| [19] | Mame William Louis, Claude Tournier. A wave signature based method for the prediction of pressure transients in railway tunnels[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93(6): 521-531. |