2. 上海市力学在能源工程中的应用重点实验室, 上海 200072
2. Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai 200072, China
0 引 言
机翼作为地效飞行器的主要升力面,其空气动力学特性与流动结构之间具有密切的相关性,并对飞行器性能产生最直接的影响。深入了解机翼近地面的流动结构及其演化规律,对于揭示地面效应的物理本质具有重要意义。众所周知,当机翼靠近地面或水面飞行时,相比在自由空间中飞行,往往能获得更大的升阻比。因此,地效飞行器比普通飞行器具有更高的能源利用率。为此已经在相关领域开展了许多研究工作,对于地面效应的空气动力学特性及流动基本规律有了相当多的认识。
李盾[1]等用数值模拟的方法发现在间隙比足够小、攻角足够大时,气流受地面和机翼下翼面的挤压,很难立即流向外侧,这会使飞行器底部的压力增高,升力增加,产生正地面效应。但是当小于某攻角飞行时,升阻比急剧下降,产生负效应。Ahmed[2]等进行的NACA4412机翼动地板地效实验研究也发现——在低高度小攻角情况下机翼下翼面产生负地面效应,他们认为下翼面与地面形成的先收缩后扩张的狭窄流道是产生负地面效应的原因。此外还有更多的针对波浪地面地效规律的研究报告。陈新[3]等的数值计算结果表明:机翼扰动在自由表面上的兴波幅度非常小,可以忽略不计;当考虑波浪水面对机翼气动力的影响时,可用“刚性”波浪地面代替“柔性”的波浪水面。Byelinskyy V G[4]等计算了使用刚性波浪地面替换柔性波浪水面所造成的误差,其结果不超过1%;测量了机翼在硬质波浪地面附近水动力特性随间隙及攻角变化的规律,发现在正弦波浪地面上方运动的机翼其受力情况的变化曲线并不符合正弦规律,其受力极值的出现位置比机翼前缘到达波峰的时刻略超前。Zhang Xin[5]等使用PIV及LDA对机翼地面效应进行实验研究,研究指出翼尖涡特性和上翼面的流动分离会改变地面效应下机翼的气动力特性,在机翼装有端板时升力增加,翼尖涡诱导的下洗能减弱翼尖附近的流动分 离。Jung Kwang Hyo[6]等利用烟线装置对NACA6409机翼进行了地面效应实验研究,实验直观地观察了翼尖涡的产生和演化过程,结果显示受地面效应影响,间隙比越小翼尖涡越被抑制。Hiemcke[7] 在风洞中测量在地面效应下NACA5312翼型表面的压力分布,发现在大攻角、小间隙高度飞行时上翼面尾缘流动分离被抑制。屈秋林[8]等数值模拟了地效飞行器近波浪表面飞行的分离流场,结果显示波浪表面飞行的气动力平均值和水平地面飞行气动力平均值随飞行高度变化的规律一致,在波浪表面附近飞行,上翼面流动分离的范围和翼剖面压力分布均呈周期性变化。
以往的多数机翼地面效应风洞实验均采用固定地板或动地板装置,难以避免地面边界层对流场的干扰,使流场结果与实际流动情况不符。对于固定地板实验,机翼相对于地面静止,这使得实验模拟的运动关系并不真实,同时在机翼距离地面较低的情况下,机翼很可能已经处于地面产生的边界层中。动地面虽然能模拟真实的机翼相对地面的运动关系,但是由于地面存在震动,长时间运动地板会发热等,均对地面附近的流场产生影响。为避免上述问题,本研究采用水槽拖曳实验模拟机翼地面效应。实验以文献[3, 4]的研究结果为依据,采用文献[4]的实验方法,将机翼模型在水平底面或正弦波形底面上拖曳,以水为介质模拟空气、硬质水平地板和波浪状地板模拟平静水面和波浪水面,使得实验所模拟的相对运动关系与实际飞行状况相同。同时,由于使用了水模拟空气介质,可以在较小的拖曳速度下获得一个相对大的雷诺数Re=2.0×105。实验使用高速PIV系统测量机翼翼尖涡速度矢量分布,以期从流场结构与翼载荷的相关性来探究地面效应的机理。需要指出的是,文献[4]实验侧重于对机翼在水平和波浪地面附近的升力阻力特性及规律的研究,尤其是受力的相位与波浪地面相位之间的关系,但没有研究机翼绕流的流场结构,且实验雷诺数达Re=1×106。而本实验雷诺数略低,而且与文献[4]的最大区别在于更关注的是机翼流场结构的测量及其与机翼升力阻力之间的关系。 1 实验装置
实验用拖曳水槽尺寸为6 m×0.5 m×0.5 m,侧壁均为平面玻璃。水平地面效应实验即以水槽玻璃 底面为实验地面。波浪地面效应实验采用波高0.02 m、 波长0.16 m的特制橡胶正弦波浪板拼接铺满水槽底,橡胶板与水槽底面同宽,表面光洁。拖曳装置为一根长6 m的直线拖曳轨道,架设于水槽一侧上方,拖曳轨道上装有滑块。滑块由伺服电机驱动同步带使之运动,运动速度及加减速时间可调,空载最大速度可达4.0 m/s,启动最大加速度可达8.0 m/s2。本实验中机翼拖曳运动速度为2.0 m/s,使用铝制NACA23012机翼,弦长c=0.1 m,展长L=0.2 m,表面光洁,以弦长为参考长度的雷诺数为Re=2.0×105。机翼升降、攻角调节及测力装置均安装于轨道滑块之上。拖曳装置如图 1(a)所示,滑块上方架设一个三角悬臂梁伸至水槽中,悬臂梁上垂直安装有行程0.2 m直线电控滑轨,用于调节机翼距水槽底面的高度,滑轨平台上装有手动攻角调节机构,同时装有夹持器,用于夹持测力天平。机翼通过导板与天平连接,导板具有对称机翼剖面,以减小对水流的扰动。机翼高度的调节精度为1 μm,攻角的调节精度为1′,高度和攻角调节装置均可锁止。
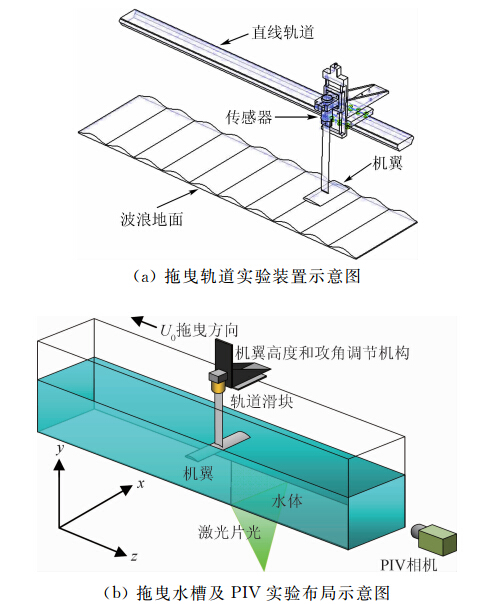 |
| 图 1 实验装置及布局示意图Fig. 1 Schematic diagram of the experimental setup |
拖曳水槽实验布局如图 1(b)所示。PIV实验光源为半导体连续激光器,输出功率3 W,波长532 nm。激光经柱透镜扩束后,形成的片光分别从水槽外侧(对波浪地形)或底部(对水平地形)照明流体内竖直截面,截面与机翼运动方向垂直。片光截面位于实验段中部距离机翼起始位置约2 m处,位置固定不变。拍摄波浪地面不同相位流场时,仅前后整体移动波浪地板,而不调节光路。PIV高速相机布置于水槽上游外0.5 m处,采用105 mm定焦镜头,拍摄方向与机翼前进方向相同。相机空间分辨率1024×1024,全画幅帧频为3000 fps。本实验中画幅宽度与片光照明区域同宽,采集频率设为500帧/s。示踪粒子采用跟随性极好且密度与水相近的尼龙微珠,对激光有良好的散射性,拍摄图像清晰,信噪比高,且在静止水中可悬浮三个小时以上保持不沉降或上浮。每组拖曳实验开始前在光面位置注入示踪粒子,待扩散均匀后,保持水体静止一小时,以保证流场湍流度足够低且每次实验的湍流度相近。PIV实验与测力实验可同时进行。定义间隙比h*为机翼后缘到水平地面高度h(或到波浪地面波浪节点高度h)与机翼弦长c的比值(h*=h/c)。本实验中水平地面间隙比工况为0.1、0.15、0.2、0.3、0.5、1.0。波浪地面间隙比工况为0.2、0.3、0.5(波浪地面时,下翼面最低点低于后缘6 mm,间隙比h*=0.1~0.15时下翼面最低点会触碰波峰表面,因此波浪地面间隙比工况最低为h*=0.2),实验几何攻角α=0°。 2 实验结果与讨论 2.1 水平地面测力结果
图 2所示为0°攻角时,机翼在水平地面附近,不同间隙比h*下的升力/阻力系数曲线。可以看出水平地面时,随着间隙比的逐渐降低,升力系数CL-flat随之减小;首先在h*=1.0~0.5段CL-flat的下降十分缓慢,升力方向向上;h*<0.5后CL-flat下降的程度加剧但机翼仍承受正向升力,并在h*=0.3附近升力接近于零;在h*<0.2时CL-flat剧烈减小并呈负值,这意味着0°攻角间隙比h*小于0.3后,机翼开始受到负升力的作用,且越靠近地面,负升力的作用越强。而阻力系数CD-flat曲线显示,随着间隙比的降低,阻力系数在较大h*范围内(h*=0.3~1.0)基本保持不变,即该h*范围内阻力系数CD-flat受地面效应的影响非常弱;只是在h*<0.2之后,CD-flat有略有增大。该测力结果与以往文献中所报道的实验或数值计算结果相吻合。波浪地面时,对测得的瞬时升力阻力曲线取周期平均值,可以看到,得到的升力系数周期均值CL-wavy和阻力系数周期均值CD-wavy整体趋势与水平地面时相近,数值上均略大于水平地面结果。
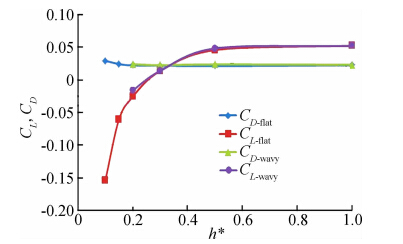 |
| 图 2 水平地面和波浪地面升力系数与阻力系数(α=0°)Fig. 2 Variation of the lift and drag coefficient CL and CD(α=0°) |
本节讨论各工况翼尖涡结构特性及差异,观察方向与机翼运动方向相同。速度矢量图中坐标参数均已无量纲化,横坐标x/c为实际空间宽度与弦长之比,机翼正中位于x/c=0处,右、左侧翼梢水平坐标分别为x/c=±1处。纵坐标y/c为实际空间高度与弦长之比,y/c=0标识位置为水平地面,机翼垂直坐标y/c在各间隙工况有所不同。坐标z/c为下游截面离开机翼后缘的距离与弦长之比,z/c=0为机翼后缘所在截面。矢量图中部空白处是由于受到垂直导板绕流对流场产生的干扰数据,因此覆盖该部分数据应不会对翼尖涡结构的分析讨论造成影响。 2.2.1 不同间隙比翼尖涡速度场对比
图 3为0°攻角,间隙比h*=1.0时机翼后缘下游z/c=1.0截面的速度矢量图。图中虚线标识了机翼后缘宽度及所在高度。可以观察到在机翼两端有两个旋转方向相反的旋涡,左侧为顺时针旋转,右侧为逆时针旋转。机翼尾流下洗明显,说明由于下翼面的压强大于上翼面,使下翼面流体绕过两侧翼尖向上翼面翻卷形成翼尖涡,从而两旋涡之间的流体诱导出强烈的下洗流动,因此机翼有效攻角小于0°,但仍大于零升攻角,使得机翼的升力为正值。因距离地面较远,旋涡的生成和发展没有受到明显抑制,其形状大致为较规则的圆形,两涡核坐标基本与两翼尖坐标重合;另外,由于诱导作用,两旋涡之间的流体速度明显大于旋涡外侧的流速。对比测力结果,也说明此时机翼受到正向升力的作用。
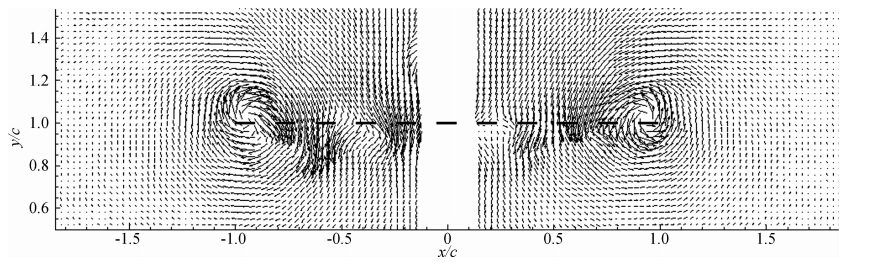 |
| 图 3 α=0°,h*=1.0,z/c=1.0时的速度矢量图Fig. 3 Tip vortex velocity fields at α=0°,h*=1.0,z/c=1.0 |
图 4为0°攻角,间隙比h*=0.3时机翼后缘下游z/c=1.0截面的速度矢量图。可以观察到该截面全场速度矢量相对于h*=1.0的工况显著减小,机翼的两端仍然有翼尖涡生成,但强度已大为减弱。两侧旋涡的旋转方向与h*=1.0时相同,其诱导的下洗运动明显削弱,同时旋涡的形状因受地面挤压,其轮廓已不再是规则的圆形,且两涡之间伴有若干小尺度二次涡。由于流体从下翼面绕过翼尖向上翼面翻转,说明下翼面压力仍大于上翼面,但是翼尖涡强度的降低说明上下翼面间的压差减小,升力降低。这与测力结果中h*=0.3时升力较h*=1.0时减小的变化趋势相吻合。
 |
| 图 4 α=0°,h*=0.3,z/c=1.0时的速度矢量图Fig. 4 Tip vortex velocity fields at α=0°,h*=0.3,z/c=1.0 |
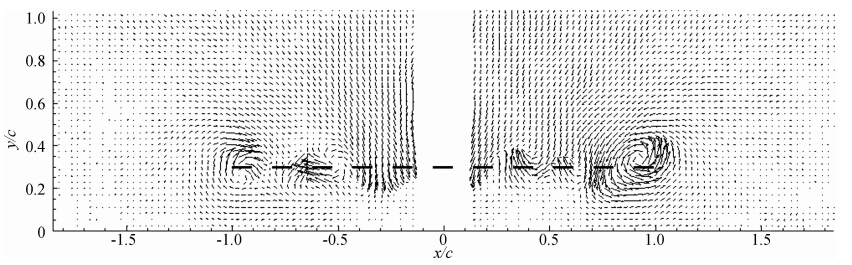
图 5为0°攻角,间隙比h*=0.1时机翼后缘下游z/c=1.0截面的速度矢量图。我们注意到该间隙比时,流场结构与前两工况完全不同。此时机翼尾流有明显上洗,流体从上翼面绕过两侧翼尖向下翼面翻卷形成翼尖涡。即左侧旋涡逆时针旋转,右侧旋涡顺时针旋转,与h*=1.0、h*=0.3两工况时的旋涡旋转方向恰好相反。同时两涡核位置已经从翼尖向机翼内侧移动了约0.2倍弦长距离,其间距明显小于h*=1.0时的情形。
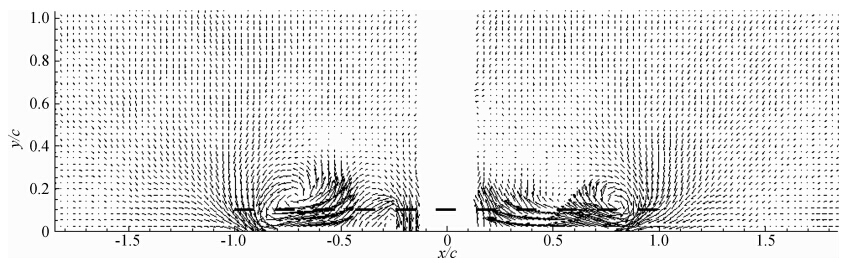 |
| 图 5 α=0°,h*=0.1,z/c=1.0时的速度矢量图Fig. 5 Tip vortex velocity fields at α=0°,h*=0.1,z/c=1.0 |
图 5进一步与图 3比较,两工况的流场结构有明显区别:1) 旋涡的形状不再是圆形,由于受到地面的挤压,旋涡的下半部分变扁;2) 同侧旋涡的旋转方向相反,说明两种工况下上下翼面的压力分布发生了相 应的变化;小间隙比时,上翼面压力大于下翼面,机翼受到负升力的作用,升力方向向下;3)虽然是处于下游的同一距离截面,但涡的移动方向及流场速度也有着明显的差异;在高间隙比h*=1.0时,翼尖涡向下游延伸的过程中,涡核不产生水平或垂向的移动,涡核间距基本保持恒定;而低间隙比h*=0.1时,旋涡在翼尖生成后,两涡核分别向机翼内侧产生明显移动,越向下游,两涡核间距越近。
对比测力曲线,流场的速度分布状况印证了机翼受到负升力的合理性,下翼面流速大于上翼面,导致下翼面压力变为吸力,机翼整体受负升力,与测力结果吻合。另外,在h*=0.1时,由于展向的流动较强,在地面表面分离形成小尺度二次涡。 2.2.2 不同间隙比翼尖涡涡量演化过程对比
图 6~图 11为0°攻角h*=0.1~1.0各间隙比时,机翼下游各截面翼尖涡瞬时涡量分布演化过程的云图,每个间隙比均截取了机翼下游z/c=0.08、0.48、1.0、2.0、3.0、4.0六个截面的涡量分布,每个截面上均有一对涡量相反的集中涡分布,图中坐标z/c=0与机翼后缘重合。
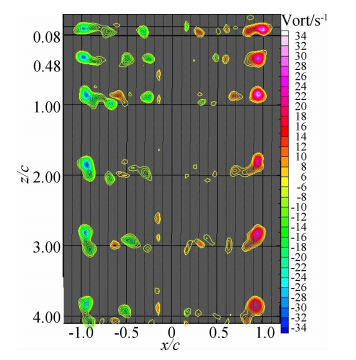 |
| 图 6 α=0°,h*=1.0时的不同截面涡核涡量分布Fig. 6 Tip vortex vorticity contours at α=0°,h*=1.0 |
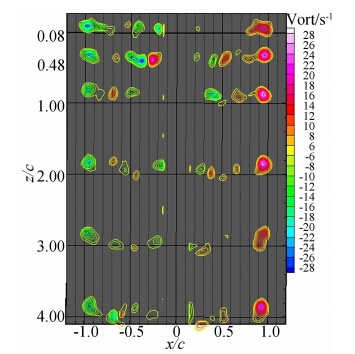 |
| 图 7 α=0°,h*=0.5时的不同截面涡核涡量分布Fig. 7 Tip vortex vorticity contours at α=0°,h*=0.5 |
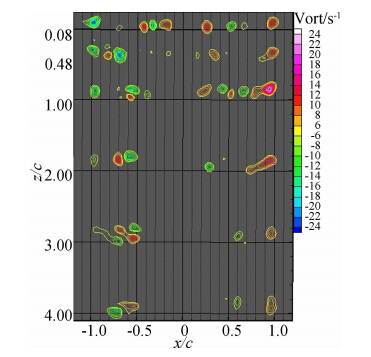 |
| 图 8 α=0°,h*=0.3时的不同截面涡核涡量分布Fig. 8 Tip vortex vorticity contours at α=0°,h*=0.3 |
图 6~图 11可以看出翼尖涡涡量Ω总的变化趋 势是:随着间隙比的减小,涡核处的最大涡量也相应 下降,表明机翼越接近地面,翼尖涡的生成和发展所 受的抑制越强,并且在向下游延伸的过程中,旋涡的 耗散速度也越快。h*=1.0时翼尖涡涡核处的最大涡量Ωmax衰减到z/c=4.0截面时的变化量ΔΩ=7;h*=0.5时为ΔΩ=9;h*=0.3时衰减量为ΔΩ=15。而h*=0.2时的情况较为特殊,涡量衰减量ΔΩ仅为6,这是由于该小间隙比时,初始时刻涡的生成 已经受到强烈抑制,涡核处最大涡量绝对值很小,机翼两端几乎没有轮廓清晰的集中涡形成,当衰减到z/c=4.0截面时,涡量几乎与静止水体的涡量相同, 翼尖涡被完全耗散,因此ΔΩ较小。h*=0.15时衰减量ΔΩ=12,h*=0.1时衰减量为ΔΩ=15。分析原因如下:从图 6~图 9中看出,随着间隙比的减小,旋涡强度只是表现出涡量上的变化和耗散速度的区别,并无流动结构上的根本改变,机翼两端的集中涡涡量都是左侧为负、右侧为正,说明在机翼的左端旋涡为顺时针、右端为逆时针,即水流从下翼面经翼尖翻转至上翼面,下翼面的压力大于上翼面,两侧翼尖涡涡核轴线均平行向下延伸,两涡间距保持不变。然而当间隙比减小到h*=0.15和h*=0.1时,如图 10、图 11所示,流动结构及涡量分布发生了本质的变化,可以发现涡量在左侧变为正值,右侧为负值,说明在机翼的左端旋涡为逆时针旋转,即上翼面水流绕过翼尖向下翼面旋转形成翼尖涡。同时在向下游发展的过程中,两端涡核不断向机翼内侧运动,涡量也逐步耗散。另外从这两个工况的结果看出,机翼越靠近地面,翼尖涡的强度越大,涡核向机翼内侧的位移也越大,两涡越靠近。
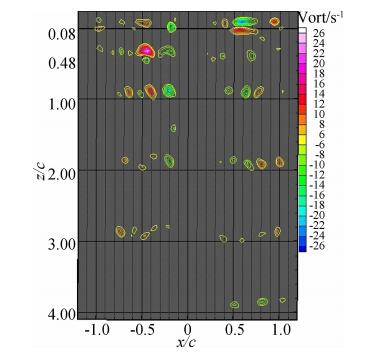 |
| 图 9 α=0°,h*=0.2时的不同截面涡核涡量分布Fig. 9 Tip vortex vorticity contours at α=0°,h*=0.2 |
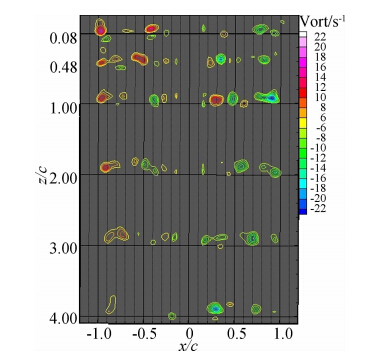 |
| 图 10 α=0°,h*=0.15时的不同截面涡核涡量分布Fig. 10 Tip vortex vorticity contours at α=0°,h*=0.15 |
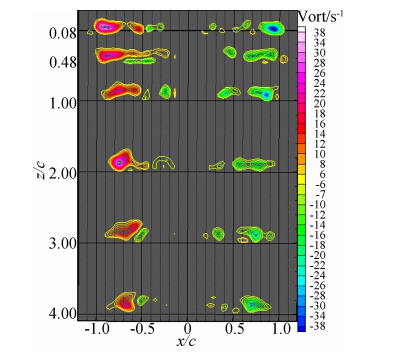 |
| 图 11 α=0°,h*=0.1时的不同截面涡核涡量分布Fig. 11 Tip vortex vorticity contours at α=0°,h*=0.1 |
对于机翼旋涡变化的现象,做如下解释:图 12所示为地面附近的0°攻角机翼剖面图,x轴代表水平地面。可以看出机翼下翼面与地面构成的流道先收缩后扩张。在流道形状固定的情况下,随着间隙比的减小,流道逐渐变得狭窄,使得下翼面的流速增加,间隙比越小流速增加越大,当间隙比降为h*=0.2时,上下翼面流速接近,压力差趋于零,机翼两端没有明显的旋涡生成。h*<0.2后,下翼面的流速即超过上翼面。同时,由于机翼逐渐靠近地面,产生的翼尖涡受到地面的挤压变形,在一定程度上抑制了翼尖涡的生成并且也加快了翼尖涡的耗散速度。
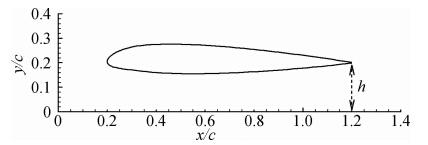 |
| 图 12 机翼及与地面形成的通道示意图Fig. 12 Side view of the wing and floor |
在正弦波浪地形不同相位的截面上,翼尖涡流场结构及其随时间的演化过程均有所区别,因此本实验研究了位于波浪地形的波峰、波谷和前后波节等典型截面处的的翼尖涡涡量随时间的变化规律,以机翼后缘掠过该截面的时刻为计时零点。首先给出每个截面计时起始时刻机翼后缘相对于波浪地面相位的示意图,如图 13所示。波浪地形波长为1.6 c,波幅0.1 c。此时定义平均间隙比h*为机翼后缘至波节的高度与弦长之比,因此后缘在波谷处的间隙比H*为H*=h*+0.1;后缘在波峰处的间隙比H*为H*=h*-0.1。
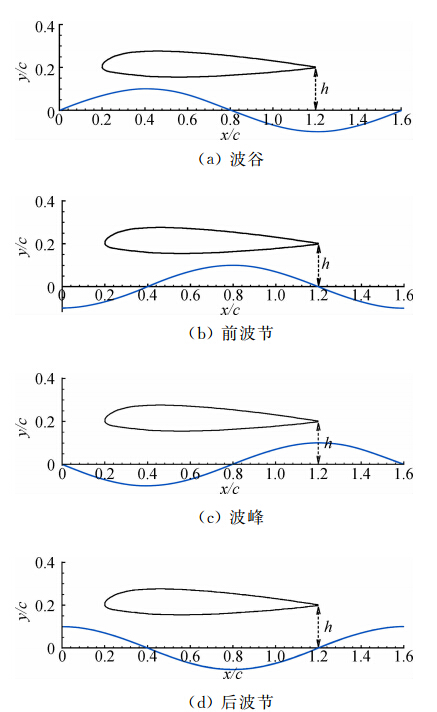 |
| 图 13 机翼后缘截面与波浪相对位置关系示意图(α=0°)Fig. 13 Schematic diagram of the relative position of the trailing edge and the wavesurface(α=0°) |
图 14~图 16为0°攻角,h*=0.2~0.5时后缘下游各截面(z/c=0.08,0.48,1.0,2.0,3.0,4.0)涡核涡量Ωcore在不同相位对比图。该涡量是将机翼两侧翼尖涡核极值取绝对值后的平均值结果。首先比较z/c=0.08截面各间隙比时结果;图 14中可以看到当后缘经过波谷时,z/c=0.08截面翼尖涡涡量为四个相位中的最大值,涡量大约为相同间隙比时水平地面值的4倍,后缘此时离开曲面实际高度为h*=0.3,是h*=0.3时水平地面涡量值的2倍,说明在机翼后缘掠过波谷的瞬间,机翼后半段与波浪地形构成的扩张通道不但没有抑制翼尖涡的生成,反而增大了其涡量值。当后缘掠过波峰后,z/c=0.08截面翼尖涡涡量最大值是同间隙比时水平地面结果的3倍;此时后缘与曲面的实际高度差为H*=h*-0.1=0.1,但是此时并没有出现水平地面时翼尖涡反向旋转的结果。再对比后缘经过后波节时的结果,得到与前两个相位类似的结果。说明这三个相位时下翼面流道在小间隙比时对地面效应的影响都是削弱的。再看图 13中前节点涡量变化曲线,其与水平地面相同间隙比时的曲线几乎重合,因此也可认为当机翼经过前波节的瞬间,下翼面流道的影响与水平地面时构成的流道对地面效应的影响相同,均为先收缩后扩张的通道。图 15、图 16中,除了后缘位于前波节时的涡量结果与水平地面相同间隙比时的情况吻合外,后缘位于其他三个相位(波峰、波谷、后波节)的结果均远大于水平地面相同间隙比时的结果,且该三个相位的最大涡量之间的差距比较小,说明这三个相位在较大间隙比时下翼面与波浪地面形成的流道虽然形状不尽相似,但地面效应的影响均已削弱且效果相近。值得注意的是,这三个相位在较大间隙比时的涡量极值均明显大于水平地面h*=1.0时的结果。图 14中,波峰、波谷、后节点三个相位处的涡量变化如曲线所示,可以看出在平均间隙比h*=0.2时,随着机翼远离该三截面,翼尖涡涡量的耗散明显加快。图 15、图 16中,各相位处涡量变化曲线下降并不明显,说明在间隙比稍大时,翼尖涡涡量的耗散速度没有加快,波浪地面对地面效应的影响亦削弱。
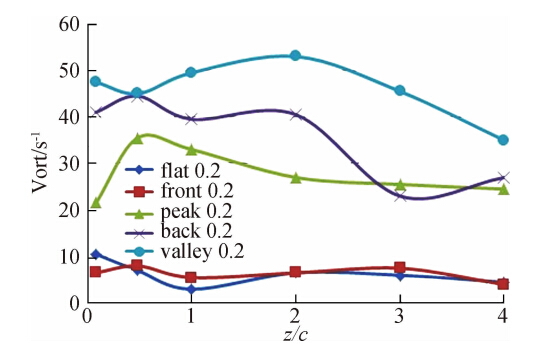 |
| 图 14 α=0°,h*=0.2时的不同截面涡核涡量Fig. 14 Variation of the vortex cores vorticity at α=0°,h*=0.2 |
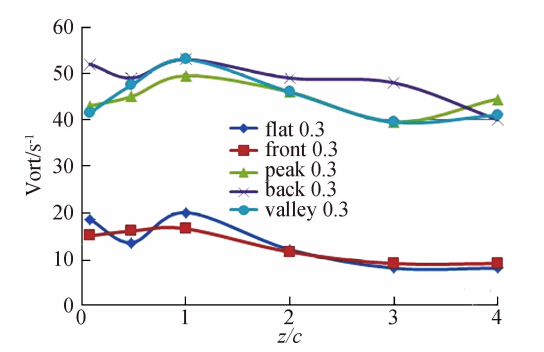 |
| 图 15 α=0°,h*=0.3时的不同截面涡核涡量Fig. 15 Variation of the vortex cores vorticity at α=0°,h*=0.3 |
取相对于波浪地面不同相位的各z/c=0.08截面涡核处涡量值Ωcore并绘成曲线,同时加入机翼波浪地面瞬时升力系数与水平地面升力系数比值的变化曲线,如图 17所示。图 17(a)为机翼波浪地面瞬时 升力系数比CL-wavy/CD-flat变化曲线,图 17(b) 为涡量变化曲线,横坐标表示机翼后缘下方波浪地面的相位,横坐标0值处为后波节。由于在三个不同间隙比下,瞬时升力系数趋势相同,此处仅讨论升力与波浪地面相位关系,故只画出一条升力变化趋势线。
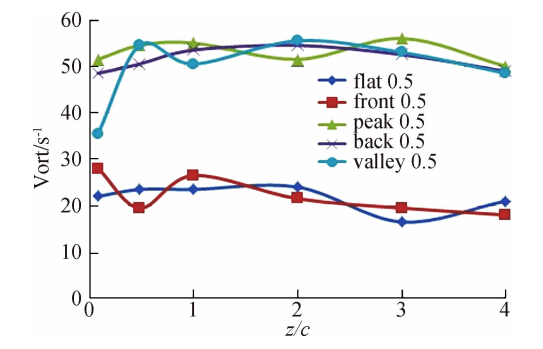 |
| 图 16 α=0°,h*=0.5时的不同截面涡核涡量Fig. 16 Variation of the vortex cores vorticity at α=0°,h*=0.5 |
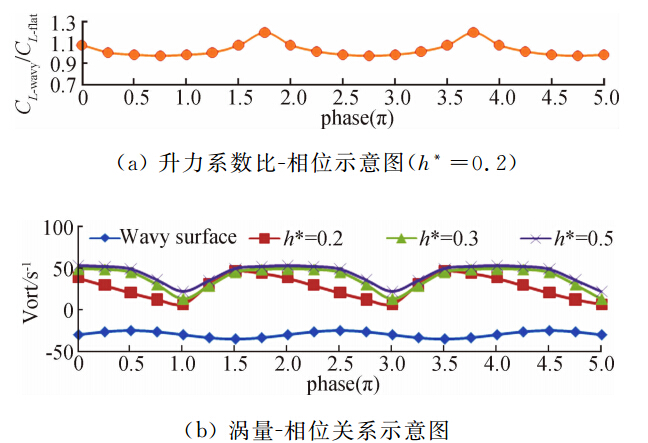 |
| 图 17 α=0°,不同间隙比下涡量和升力系数比 变化与波浪相对位置关系Fig. 17 Variation of the vortex cores vorticityand ratio of CL with the phase of the wave surface(α=0°) |
可以看到在h*=0.2时,涡量在机翼后缘经过前节点时达到最小值,随着机翼后缘不断向前运动掠过波峰、后节点和波谷,涡量不断上升至波谷时的最大值,然后再次迅速跌落至前节点处的最小值。当h*=0.3~0.5时,涡量亦在前节点达到最小值,但是随即在波峰处恢复到接近最大值的水平,在机翼后缘掠过后节点时达到最大值,在机翼后缘越过波谷后迅速下降,运动到前节点时涡量达到最小值。涡量随波浪地面相对位置的变化结果显示,在一个地形波浪周期内,涡核处涡量变化表现出明显周期性变化,但是不符合波浪地面的正弦变化规律。因此,从波浪地面与水平地面的涡核涡量Ωcore对比结果来看,除了在上坡节点(前节点)处两者相近外,波浪地面对于机翼的地面效应的影响较水平地面情况是削弱的。从波浪 地面的不同相位结果来比较,上坡节点处受地面影响 最大,此时流道形状最狭窄。在小间隙比条件下,其余节点处受地面影响程度不同,随着间隙比增大,受地面影响程度的差异迅速减小,这也是涡量测量结果不符合正弦规律的原因。而在瞬时升力系数比曲线上,可以发现当机翼后缘在后节点与波谷之间时升力达到最大值,后缘在前节点与波峰之间时升力达最小值,同时,在机翼升力增加的过程中,幅值变化明显,表现为在最大值附近曲率大而在最小值附近曲率很小。此时可以认为在后缘上坡的过程中,下翼面与地面形成的流道造成了下翼面流速的增加,导致上下翼面压力差减小,升力损失,旋涡强度减弱。当机翼后缘下坡时,后缘与地面间隙较小,下翼面流体较难迅速从流道流出,造成下翼面流体受到阻滞,速度减小,升力增加,旋涡强度增加。 3 结 论
利用拖曳水槽模拟了机翼在水平及波浪表面附近的地面效应,采用二维高速PIV系统测量了各工况下尾流场的瞬时变化过程。研究认为在0°攻角下翼尖涡流场结构受到地面与下翼面所构成的流道形状及狭窄程度的影响;并发现在水平地面附近不同飞行高度时,机翼所受正升力和负升力所对应的流场结构差异,并分析了机翼受负升力的原因。在波浪地面的测量中,获得了机翼在飞跃正弦波浪地形的过程中流场结构的变化,地面效应由于波浪地面与机翼下翼面瞬间相对相位关系的不同而不同,仅在机翼经过上坡节点时,地面效应与水平地面时相似;而在其他波浪相位时地面效应均受到削弱。同时发现正弦波浪上各相位截面翼尖涡核处涡量的变化呈现出明显的周期性,但该周期性不符合正弦变化规律,且其极值与正弦波型有相位差。这些特性对于地面效应飞行器纵向稳定性的控制具有一定的参考价值。
| [1] | Li Dun, WangYining. Three-dimension numerical simulation of the ground effect on the ground effect vehicle[J]. Flight Dynamics, 2006, 24(2): 18-21. (in Chinese) 李盾, 王义宁. 地效飞行器三维地面效应的数值模拟[J]. 飞行力学, 2006, 24(2): 18-21. |
| [2] | Ahmed M R, Takasaki T, Kohama Y. Aerodynamics of a NACA4412 airfoil in ground effect[J]. AIAA Journal, 2007, 45(1): 37-47. |
| [3] | Chen Xin, Shan Xuexiong. Numerical simulation on unsteady aerodynamics and wace making of a wing flying over offing[C]//2003 Symposium on Research Frontier of Aerodynamics. 陈新, 单雪雄. 三维机翼掠海飞行时非定常气动力和兴波的数值计算[C]//2003空气动力学前沿研究论文集. 北京: 中国宇航出版社, 2003: 132-137. |
| [4] | Byelinskyy V G, Zinchuk P I. Hydrodynamical characteristics of an ekranoplane wing flying near the wavy sea surface[C]//RTO Meeting proceedings, 1999. |
| [5] | Zhang Xin, Zeriban J, Ruhrmann A, et al. Tip vortices generated by a wing in ground effect[C]//Proceedings of the 11th International Symposium on Applications of laser Techniques to Fluid Mechanics. University of Southampton, 2007. |
| [6] | Jung K H, Chun H H, Kim H J. Experimental investigation of wing-in-ground effect with a NACA6409 section[J]. Journal of Marine Science and Technology, 2008, 13: 317-327. |
| [7] | Hiemcke C. NACA5312 in ground effect: wind tunnel and panel code studies[R]. AIAA 97-2320. |
| [8] | Qu Qiulin, Liu Peiqing, Qin Xuguo. Numerical research on separated flow around a WIG craft flying over wavy ground at high incidence angle[J]. Acta Aerodynamica Sinica, 2008, 26(2): 221-226. (in Chinese) 屈秋林, 刘沛清, 秦绪国. 地效飞行器近波浪地面大迎角飞行分离流动数值研究[J]. 空气动力学学报, 2008, 26(2): 221-226. |
| [9] | Qu Qiulin, Liu Peiqing, Qin Xuguo. Numerical research on aerodynamic characteristics of WIG craft flying over wavy ground [J]. Acta Aeronautica et Astronauticasinica, 2007, 28(6): 1327-1333. (in Chinese) 屈秋林, 刘沛清, 秦绪国. 地效飞行器波浪地面飞行气动性能数值研究[J]. 航空学报, 2007, 28(6): 1327-1333. |
| [10] | Im Y H, Chang K S. Unsteady aerodynamics of a wing in ground effect airfoil flying over a wavy wall[J]. Journal of Aircraft, 2000, 37(4): 690-696. |
| [11] | Sun Ruimin, Daichin. Experimental investigation on tip vortices and aerodynamics of a wing in ground effect[J]. Theoretical and Applied Mechanics Letters, 2011, 1(3): 1-6. |
| [12] | Yang Wei, Yang Zhigang. Aerodynamic investigation of a 2D wing and flows in ground effect[J]. Chinese Journal of Computational Physics, 2009, 26(2): 231-240. |
| [13] | Rozhdestvensky K V. Wing-in ground effect vehicles[J]. Progress in Aerospace Sciences, 2006, 42: 211-283. |
| [14] | Zhang Xin, Zeriban J. Aerodynamics of a single element wing in ground effect[J]. Journal of Aircraft, 2000, 37(6): 1058-1064. |
| [15] | Harvey J K, Perry F J. Flowfield produced by trailing vortices in the vicinity of the ground[J]. AIAA Journal, 1971, 9(8): 1659-1660. |



