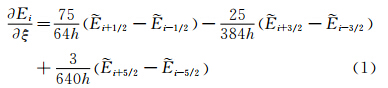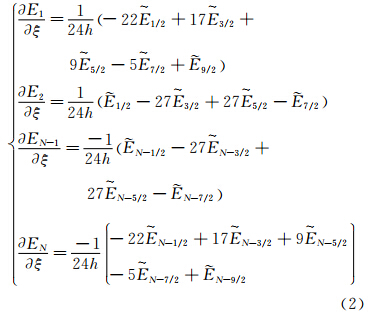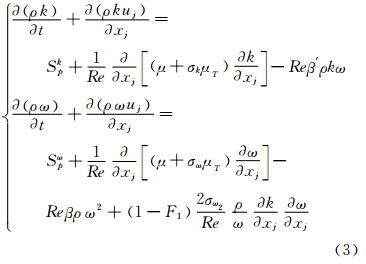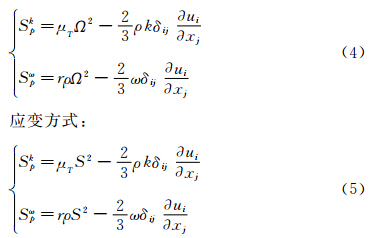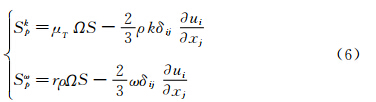2. 中国空气动力研究与发展中心 空气动力学国家重点实验室, 四川 绵阳 621000
2. State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang 621000, China
0 引 言
基于雷诺平均的Navier-Stokes方程(RANS)的模拟方法、大涡模拟方法和直接数值模拟方法是湍流问题数值模拟研究的主要手段。受当前可获得的高性能计算机资源的制约，基于RANS方程的数值模拟方法依然是飞行器气动设计中主要采用的湍流模拟方法[1, 2, 3, 4]。高阶精度格式具有高分辨率、低耗散、低色散等特点，目前主要应用于简单构型的复杂流动机理研究，在复杂构型的工程应用方面依然处于探索阶段[5, 6, 7]。基于RANS方程和有限差分方法，通过在面积守恒律、边界格式等方面的研究工作[8, 9]，邓小刚提出的加权紧致非线性格式(WCNS)在复杂构型上的应用研究取得了重要进展[10, 11]，显示了WCNS格式在流动细节刻画、阻力及最大升力系数等关键气动特性预测等方面的潜在优势。
Menter SST[12]两方程模型是目前求解RANS方程最常用的湍流模型之一。依据对驻点附近、空间旋涡和剪切层流动的不同认识，SST湍流模型中的生成项有三种表达方式[13]，分别是涡量形式(Vorticity)、应变方式(Strain)及涡量与应变相结合的混合方式(Hybrid)。在文献[14]中，本文作者采用WCNS格式和跨声速RAE2822翼型、DLR-F6翼身组合体构型，开展了SST湍流模型不同湍流生成项对跨声速流动数值模拟影响的高精度计算分析，本文的研究工作是此项工作的继续。
基于五阶 空间离散精度的WCNS格式和Menter SST 两方程湍流模型，本文开展了不同湍流生成项表达方式对低速流动数值模拟的影响研究。研究内容主要包括两个方面：采用低速NLR7301两段翼型，从收敛历程、边界层湍流粘性系数分布、边界层速度分布、压力系数分布、气动特性等多方面，开展了不同湍流生成项表达方式对二维低速翼型数值模拟影响的计算分析；采用低速Trap Wing高升力构型，从收敛历程、压力系数分布、气动特性等方面，开展不同湍流生成项表达方式对三维高升力构型数值模拟影响的计算分析。 1 高阶精度计算方法与湍流模型
基于任意坐标系下的RANS方程组和多块对接结构网格技术，本文采用的高阶精度计算方法归纳为：平均流动控制方程对流项离散采用五阶精度的WCNS格式，粘性项离散采用六阶精度中心格式，边界及近边界条件采用单边四阶精度离散；湍流模型采用Menter SST两方程模型，湍流模型及边界条件的离散采用与平均流动控制方程相同的高阶精度离散方法。以下简单介绍五阶空间离散精度的WCNS格式及四阶精度的边界及近边界格式，详细介绍可参见文献[8]。设网格间距为h，以ξ方向为例，WCNS格式可表示为：
四阶精度的边界及近边界格式表示为： 其中，Ei/ξ为计算节点处的无粘通量导数，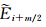
为半节点处的无粘通量。
湍流模型采用Menter SST两方程模型，该湍流模型的守恒形式可表达式为[13]：
方程(3)右端的三项分别为湍流生成项、扩散项与破坏项。湍流生成项具体有以下三种表达方式：
涡量方式：
混合方式：
其中Ω=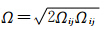
为涡量的模，S= 
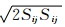为应变的模，方程中各项的详细介绍见文献[14]。
2 研究模型与计算网格
NLR7301两段翼型由主翼 和襟翼组成，襟翼偏角为20°，主翼和襟翼之间的间隙宽度(gap)为0.026c (c为弦长)，重叠区域长度为0.053c。风洞试验是在荷兰NLR 3m×2m低速风洞中完成的[15]。多块对接结构局部网格拓扑和计算网格见图 1，网格节点总数为192655，y+≈1.0，网格收敛性的研究结果参见文献[16]。
 |
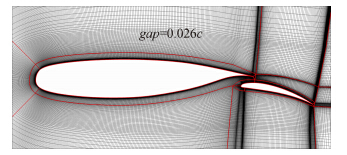| 图 1 NLR7301两段翼型的计算网格(局部)Fig. 1 Computational grid for NLR7301 two-element airfoil (local) |
Trap Wing高升力构型是安装在简化机身上的大弦长、中等展弦比、前缘缝翼/主机翼/后缘襟翼三段构型。前缘缝翼与后缘襟翼的偏角分别为30°和25°。网格规模为1.465×107，网格收敛性的研究结果参见文献[11]。风洞试验是在NASA Langley 14×22 英尺亚声速风洞中完成的[17]。计算构型表面网格、网格拓扑及局部网格见图 2。
 |
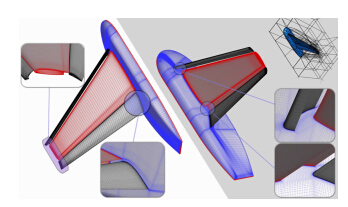| 图 2 梯形翼构型计算网格Fig. 2 Computational grid for Trap Wing configuration |
采用高阶精度计算方法，从收敛历程、表面压力 系数分布、典型站位湍流粘性系数分布和气动特性等方面研究SST两方程不同湍流生成项表达方式对NLR7301两段翼型高阶精度数值模拟的影响。计算来流条件为：Ma=0.185，α=13.1°，Re=2.51×106。 3.1 收敛历程
图 3给出了采用不同湍流生成项表达方式得到的NLR7301两段翼型残差收敛曲线，其中横坐标为迭代步数(Iteration)、纵坐标为平均残差的自然对数(Log(Resave))。
 |
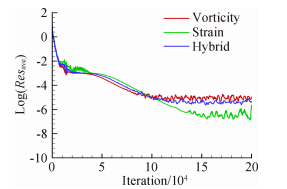| 图 3 NLR7301两段翼型计算残差收敛历程Fig. 3 Convergence history of numerical simulation for NLR7301 two-element airfoil |
从图 3中可以看出：对于NLR7301低速绕流，采用涡量形式(Vorticity)计算得到的收敛精度比采用应变量形式(Strain)计算得到的收敛精度要低，采用混合形式(Hybrid)计算得到的收敛精度介于二者的之间。 3.2 边界层物理量分布
图 4给出了NLR7301翼型典型站位边界层内湍流粘性系数分布和速度型曲线，其中，速度型曲线包括了试验结果。NLR7301翼型的站位为x/c=0.60、xf /c=0.119。图中横坐标分别为无量纲湍流粘性系数(μt/μ∞)、x方向速度(u/u∞)，纵坐标为无 量纲物面法向距离(y/c)。在充分发展的湍流区(x/c =0.60)和包含了主翼尾迹区的尾翼上表面(xf/c=0.119)站位，采用不同湍流生成项得到的粘性系数分布和速度分布差异很小，但速度分布与试验结果差异明显，采用转捩模型可以提高计算结果与试验的吻合程度[18]。
 |
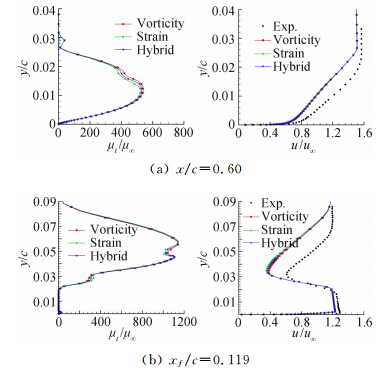| 图 4 NLR7301两段翼型边界层内物理量分布Fig. 4 Distribution of physical parameters in boundary layer for NLR7301 two-element airfoil |
图 5为NLR7301翼型的压力系数分布曲线与测压试验结果的比较。
 |
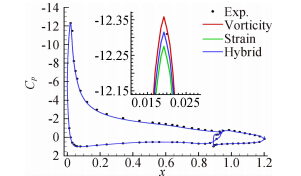| 图 5 NLR7301两段翼型表面压力系数分布Fig. 5 Cp distribution on surface for NLR7301 two-element airfoil |
不同湍流生成项表达方式对主翼头部的吸力峰值有一定影响，对其他位置的压力系数分布影响很小。湍流生成项采用涡量形式得到的吸力峰值比采用应变形式得到的吸力峰值要大，采用涡量与应变混合形式得到的吸力峰值介于二者之间。 3.4 气动特性
表 1给出了不同湍流生成项表达方式下NLR7301翼型的气动力结果。湍流生成项采用涡量形式计算得到的升力系数CL、摩擦阻力系数CDf和低头力矩系数比采用应变形式得到的计算结果略大。压差阻力系数CDp比应变量形式的小，这是由于前者计算得到的主翼前缘吸力峰值较大造成的(见图 5)。湍流生成项采用应变与涡量混合形式的计算结果介于单独采用二者的计算结果之间。采用转捩模型可以提高计算结果与试验的吻合程度[18]。
| Sp | CL | CD | CDf | CDp | Cm |
| Vorticity | 3.064 | 0.06005 | 0.00878 | 0.05127 | -0.4395 |
| Strain | 3.049 | 0.06125 | 0.00844 | 0.05281 | -0.4377 |
| Hybrid | 3.056 | 0.06067 | 0.00860 | 0.05207 | -0.4385 |
| Exp. | 3.141 | 0.0445 | / | / | -0.440 |
采用高阶精度计算方法，从收敛历程、典型站位压力系数分布和气动特性等方面研究SST两方程不同湍流生成项表达方式对Trap Wing高升力构型高阶精度数值模拟的影响。计算来流条件为：Ma=0.20，α=13°，Re=4.30×106。 4.1 收敛历程
图 6给出了采用不同湍流生成项得到的Trap Wing高升力构型残差收敛曲线。从图中可以看出：对于Trap Wing高升力构型低速绕流，采用三种湍流生成项组合方式得到的残差收敛历程略有不同，但最终的收敛精度基本一致。
 |
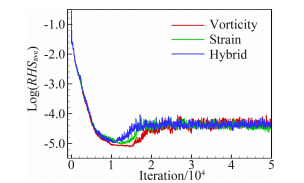| 图 6 Trap Wing高升力构型计算残差收敛历程Fig. 6 Convergence history of numerical simulation for Trap Wing high-lift configuration |
图 7为采用不同湍流生成项得到的Trap Wing高升力构型展向典型站位y/c压力分布与测压试验结果的比较。
不同湍流生成项表达方式对靠近机身的展向站位(y/c=0.17)、机翼中间的站位(y/c=0.50)和靠近翼梢的站位(y/c=0.85)上的压力分布基本没有影响，且与试验值吻合良好。不同湍流生成项组成方式对翼梢的站位(y/c=0.98)压力分布影响明显。其中湍流生成项采用涡量形式得到的主翼后部与襟翼前缘的吸力峰值比采用应变形式得到的吸力峰值要大，采用涡量与应变混合形式得到的吸力峰值介于二者之间。这主要是由于不同湍流生成项组成方式对翼梢涡模拟精度的不同导致的。
 |
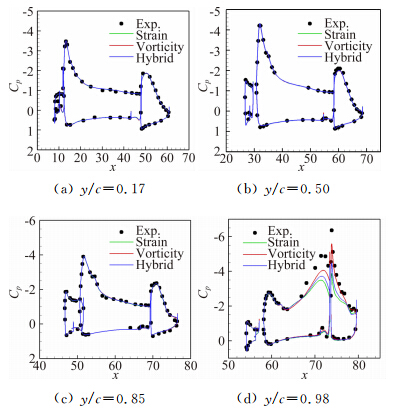| 图 7 梯形翼构型典型站位压力分布Fig. 7 Cp distribution at typical span sections of Trap Wing configuration |
表 2给出了Trap Wing高升力构型采用不同湍流生成项表达方式得到的气动力计算结果。不同湍流生成项对升力系数基本无影响，对阻力系数和低头力矩系数略有影响，其中采用涡量方式得到的气动力系数更加接近试验值。采用转捩模型可以进一步提高气动力系数与试验结果的吻合程度[19]。
| Sp | CL | CD | CDf | CDp | Cm |
| Vorticity | 2.007 | 0.3225 | 0.0119 | 0.3106 | -0.4789 |
| Strain | 1.997 | 0.3206 | 0.0117 | 0.3089 | -0.4721 |
| Hybrid | 2.005 | 0.3220 | 0.0118 | 0.3102 | -0.4762 |
| Exp. | 2.047 | 0.3330 | / | / | -0.5032 |
(1) 不同湍流生成项对低速二维流动的收敛历程有比较明显的影响，对低速三维流动的收敛历程影响不明显；
(2) 对于低速二维流动，不同湍流生成项对附面层湍流粘性系数和速度型影响不明显；
(3) 对于低速二维流动，不同湍流生成项主要影响主翼前缘的吸力峰值，进而影响相应的升力系数和压差阻力系数；对于低速三维流动，不同湍流生成项主要影响翼梢涡的模拟精度，进而影响压差阻力系数；
(4) 综合考虑收敛历程与数值模拟结果，对于低速附着流动或小分离流动，建议湍流生成项选择应变与涡量的混合方式。
致谢: 感谢张玉伦、王光学、孟德虹在高阶精度算法程序实现方面的工作。
| [1] | Rumsey C L, Ying S X. Prediction of high lift: review of present CFD capability[J]. Progressin Aerospace Sciences, 2002, 38: 145-180. |
| [2] | Tinoco E N, Bogue D R, Kao T J, et al. Progress toward CFD for full flight envelope[J]. The Aeronautical Journal, 2005, 109: 451-460. |
| [3] | Johnson F T, Tinoco E N, Yu N J. Thirty years of development and application of CFD at Boeing commercial airplane[J]. Computers&Fluids, 2005, 34: 1115-1151. |
| [4] | Slotnick J, Khodadoust A, Alonso J, et al. CFD vision 2030 study: a path to revolutionary computational aerosciences[R]. NASA CR 2014-218178. Hampton: NASA, 2014. |
| [5] | Visbal R M, Gaitonde D V. On the use of higher-order finite-difference schemes on curvilinear and deforming meshes[J]. J. Com. Phys., 2002, 181: 155-185. |
| [6] | Nonomura T, Iizuka N, Fujii K. Freestream and votex preservation properties of high-order WENO and WCNS on curvilinear grids[R]. Computers&Fluids, 2010, 39: 197-214. |
| [7] | Kroll N, Bieler H, Deconinck H, et al. ADIGMA-A European initiative on the development of adaptive high-order variational methods for aerospace application[R]. Springer, 2010. |
| [8] | Deng X G, Zhang H X. Developing high-order weighted compact nonlinear schemes[J]. J. Com. Phys., 2000, 165: 24-44. |
| [9] | Deng X G, Min R B, Mao M L, et al. Further studies on geometric conservation law and application to high-order finite difference scheme with stationary grid[J]. J. Com. Phys., 2013, 239: 90-111. |
| [10] | Wang G X, Deng X G, Liu H Y, et al. Application of high-order scheme(WCNS) at high angles of incidence for delta wing[J]. Acta Aerodynamica Sinica, 2012, 30(1): 28-33. (in Chinese) 王光学, 邓小刚, 刘化勇, 等. 高阶精度格式WCNS在三角翼大攻角模拟中的应用研究[J]. 空气动力学学报, 2012, 30(1): 28-33. |
| [11] | Li S, Wang G X, Zhang Y L, et al. Numerical simulation of trapezoidal wing high lift configuration with WCNS-E-5 scheme[J]. Acta Aerodynamica Sinica, 2014, 32(4): 439-445. (in Chinese). 李松, 王光学, 张玉伦, 等. WCNS格式在梯形翼高升力构型模拟中的应用研究. 空气动力学学报, 2014, 32(4): 439-445. |
| [12] | Menter F R. Two-equation eddy-viscosity turbulence models for engineering application[J]. AIAA Journal, 1994, 32(8): 1598-1605. |
| [13] | Menter F R, Kuntz M, Langtry R. Ten years of industrial experience with the SST turbulence model, turbulence, heat and mass transfer[R]. Begell House Inc., 2003: 625-632. |
| [14] | Wang Y T, Sun Y, Wang G X, et al. Numerical study of the effect of turbulent production terms on the simulation of transonic flows with high-order numerical method[J]. Acta Aerodynamica Sinica, 2015, 33(1): 25-30. (in Chinese). 王运涛, 孙岩, 王光学, 等. 高阶精度方法下的湍流生成项对跨声速流动数值模拟的影响研究[J]. 空气动力学学报, 2015, 33(1): 25-30. |
| [15] | Van Den Berg B. Boundary Layer measurements on a two-dimensional wingwith flap[R]. NLR TR 79009 U. Amsterdam: NLR, 1979. |
| [16] | Wang Y T, Sun Y, Wang G X, et al. Numerical analysis of the effect of discrete order of turbulence model on numerical simulation[J]. Acta Aeronautica et Astronautica Sinica, 2014. (accepted, in Chinese) 王运涛, 孙岩, 王光学, 等. 湍流模型离散精度对数值模拟影响的计算分析[J]. 航空学报, 2014.(录用). |
| [17] | Johnson P L, Jones K M, Madson M D. Experimental investigation of a simplified 3D high lift configuration in support of CFD validation[R]. AIAA 2000-4217. Reston: AIAA, 2000. |
| [18] | Meng D H, Zhang Y L, Wang G X, et al. Application of γ-Reθ transition model to two-dimensional low speed flows[J]. Acta Aeronoutica et Astronautica Sinica, 2011, 32(5): 792-801. (in Chinese) 孟德虹, 张玉伦, 王光学, 等. γ-Reθ转捩模型在二维低速问题中的应用[J]. 航空学报, 2011, 32(5): 792-801. |
| [19] | Rumsey C L, Long M, Stuever R A. Summary of the first AIAA CFD high lift prediction workshop(invited)[R]. AIAA 2011-939. Reston: AIAA, 2011. |