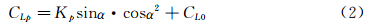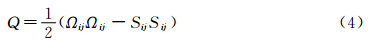飞翼布局取消了常规布局中的垂尾和平尾等部件,因而提升了气动效率,而且还具有优良的隐身能力和结构性能[1],但是,安定面缺失和操纵效能不足等问题在很长时间内限制了飞翼布局的发展。随着现代控制技术的发展和新的设计理念的出现,飞翼布局的缺陷能够在一定范围之内得到有效抑制,这使得飞翼布局逐渐走向实用化成为可能,美国的B-2远程轰炸机是大展弦比飞翼布局成功应用的典型案例。近年来,世界各国竞相开展无人作战飞机(UCAV)的研制,如美国的X-45A/B/C、X-47A/B,欧洲多国研制的“神经元”和英国的雷神无人机等,这些无人作战飞机都不约而同地采用了中等展弦比飞翼布局,飞翼布局所受的重视程度由此可见一斑。与此同时,欧美各国推出了多个具有飞翼布局特征的通用研究模型,如洛克希德·马丁公司设计的ICE飞翼布局新型控 制面模型[2]、波音公司设计的UCAV1301/1302/1303飞翼布局系列[3]、欧洲主导美国参与的SACCON 通用飞翼研究布局[4]等,基于对这些飞翼布局通用研究模型流动机理的研究,可以获得类似的飞翼布局飞机的典型流动特性,为无人作战飞机的研制提供技术支撑。从公开的文献资料看,国内对飞翼布局已经就布局概念设计、开裂式方向舵、全动翼尖、喷流控制等若干问题开展了研究[5, 6, 7, 8],但没有统一的通用飞翼布局外形研究平台,尚未形成完整的研究体系。
众所周知,通过减小展弦比、增大前缘后掠角可以减小超声速飞行时的激波阻力,而未来飞行器更高的飞行速度需求会促使飞翼布局朝着小展弦比的方向发展,为此,国内有关研究机构自主设计了小展弦比飞翼标模,作为小展弦比融合体飞翼外形的通用研究平台。该模型在中国空气动力研究与发展中心1.2m亚跨超声速风洞完成了常规测力试验,试验结果表明小展弦比飞翼标模在跨声速迎角4°开始出现非线性升力,在迎角12°至16°范围内会出现升力突然下降、俯仰力矩曲线突然上扬的现象。为了分析该现象的机理,采用CFD方法研究分析了小展弦比飞翼标模在马赫0.9时的典型流动特性,主要以涡升力为出发点,分析了涡的产生、发展直至破裂的整个过程。 1 数值模拟方法
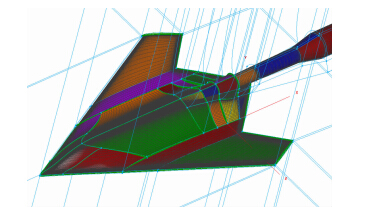
小展弦比飞翼标模具有65°前缘后掠角,采用变前缘设计方法,后缘后掠角为±47°,展弦比为1.54,几何外形如图 1所示。针对该标模的试验外形生成了一套总网格数量为800万量级的计算网格,采用OH型拓扑结构,网格远场距离物面的距离均大于模型全长的十倍。通过前期研究发现模型空腔的模拟与否对结果的影响很小,可以忽略,因而本次研究并没有模拟模型空腔。网格结构如图 2所示。
 |
| 图 1 小展弦比飞翼标模Fig. 1 Low-aspect-ratio flying-wing |
 |
| 图 2 网格Fig. 2 Grids |
数值求解采用的控制方程为雷诺平均N-S方程,空间离散方法为有限体积法,空间无粘通量采用ROE格式进行离散,粘性通量采用二阶中心差分格式离散,时间项采用隐式LU-SGS方法求解。为了加快收敛速度,还采用了局部时间步长和多重网格技术。湍流模型为k-ω SST二方程模型。物面采用无滑移边界条件,远场采用无反射边界条件。
计算无量纲系数所采用的参考面积为0.234 m2,纵向参考长度和雷诺数参考长度都是平均气动弦长0.503 2 m,参考重心为45%平均气动弦长处,计算马赫数为0.9,雷诺数为8.7×106,上述参数都与风洞试验保持一致。计算与试验结果的对比验证详见下一节。 2 基本升力特性分析与验证
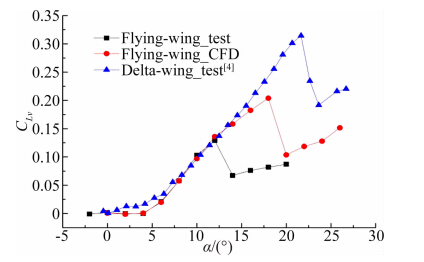
65°平板三角翼作为一个广为人知的公开外形,前人已对其进行了大量研究[9, 10, 11]。65°平板三角翼的典型气动特性是机翼背风面受前缘涡的影响会出现一个低压区,从而产生涡升力,跨声速时前缘涡会在迎角22°至26°范围内发生涡破裂导致升力突然下降、俯仰力矩曲线突然上扬。本文所研究的小展弦比飞翼标模其前缘后掠角同样为65°,因而具有与65°三角翼相似的一些气动特性,可以采取一些类似的手段来分析其异同。
马赫数0.9时升力系数随迎角的变化曲线如图 3所示。图 3中三条曲线分别表示小展弦比飞翼标模的风洞试验结果、CFD计算结果以及NASA的65°平板三角翼的试验结果[9]。从图 3中可以看出,飞翼标模的零升迎角为负值,相比平板三角翼小2°左右,这是由于飞翼标模的截面翼型具有弯度所致。对于飞翼标模,在迎角4°以前,升力系数保持较好的线性度,迎角4°以后开始出现明显的涡升力,在所研究的迎角范围内,飞翼标模的升力非线性现象相比平板三角翼更明显。此外,飞翼标模在某一特定迎角范围出现升力突然下降,此现象类似于平板三角翼,但出现此现象的迎角小于平板三角翼的涡破裂迎角,且计算得到的临界迎角与试验结果也有较大差异。
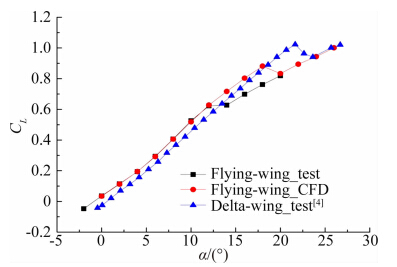 |
| 图 3 升力系数Fig. 3 Lift coefficient |
为了更详细地观察涡升力的变化,采用波尔豪森[12](Polhamus)提出的前缘吸力比拟法将升力分解为位流升力和涡升力之和,公式描述为:
其中,CLp表示位流升力系数,CLv表示涡升力系数。由于飞翼标模的截面翼型具有弯度,0°迎角时升力不为0,因此本文对波尔豪森提出的升力分解公式作了部分修正,增加了一个表示0°迎角升力系数的常数项CL0,使其更加适应于本文所讨论的问题。最终位流升力系数的计算公式为:而涡升力系数表达式则沿用经典前缘吸力比拟法的结果:
按照上述方法得到的涡升力系数曲线如图 4所示。从图 4中可以发现,平板三角翼在小迎角时即有涡升力出现,逐渐增加直到22°涡破裂;而飞翼标模在迎角小于4°时几乎没有涡升力,迎角大于4°以后涡升力急剧上升,随着迎角逐渐增大,CFD结果和试验结果分别在迎角18°和12°出现涡升力突然下降,不论CFD还是试验得到的临界迎角都明显小于平板三角翼的临界值。为了进一步研究其原因,需对流场进行深入分析。
 |
| 图 4 涡升力系数Fig. 4 Vortex lift coefficient |
CFD与试验结果得到的临界迎角差异较大的原因,主要是由于涡破裂包含了非常复杂的流动,目前尚没有可靠的数值模拟方法能够准确捕捉涡破裂临界迎角,即使采用同一模型在不同风洞进行试验也难以获得一致的结果,尤其是在跨声速时由于激波的出现进一步增加了流动的复杂程度。考虑到CFD方法捕捉到的规律与试验类似,且在迎角小于12°和大于20°的计算范围内CFD结果与试验值吻合良好,又由于CFD得到的流场信息远多于风洞试验结果,因此,本文采用CFD方法对小展弦比飞翼标模的典型流动特性开展进一步研究。 3 涡的产生、发展和破裂 3.1 旋涡判别准则
Hunt[13]在1988年提出了一种判别涡结构的方法,其基本表达式是:
其中,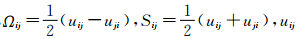 是流场速度的导数,为一个二阶张量,Ωij和Sij则分别是该张量的反对称和对称部分,物理上来说分别表示其旋转分量和应变率分量。满足Q值为正的等值面即为涡环。已有研究表明[14],用Q值来判别涡的结构有较高的可靠性和精细度。
3.2 涡的产生和发展
是流场速度的导数,为一个二阶张量,Ωij和Sij则分别是该张量的反对称和对称部分,物理上来说分别表示其旋转分量和应变率分量。满足Q值为正的等值面即为涡环。已有研究表明[14],用Q值来判别涡的结构有较高的可靠性和精细度。
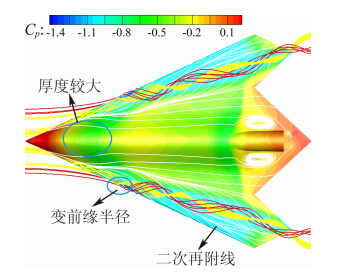
3.2 涡的产生和发展前文由升力系数曲线推断飞翼标模在迎角大于4°以后开始产生涡升力,通过对表面和空间流线的观察可以证实这一结论。从图 5中可以发现,迎角4°时在翼稍附近开始有局部分离。随着迎角的增大,到迎角6°时,从图 6可以看出,分离位置迅速前移,前缘分离点已经移动至前缘半径发生明显变化的位置,分离区受涡的影响有明显的展向流动,并形成低压带,使得升力增加。
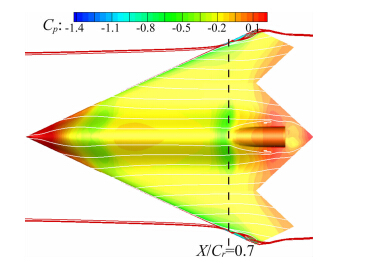 |
| 图 5 迎角4°时的流线和压力云图Fig. 5 Streamlines and Cp at α=4° |
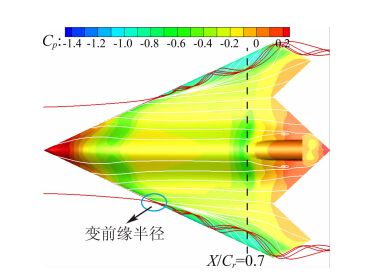 |
| 图 6 迎角6°时的流线和压力云图Fig. 6 Streamlines and Cp at α=6° |
此外,从图 5和图 6中表面压力系数分布可以看出,在沿流向X/Cr=0.7位置出现了一道明显的激波。
随着迎角的继续增大,主涡向内移动,分离区逐渐增大,涡升力持续增加。由图 7可以看出,迎角12°时,机头处厚度较大的区域使得流线发生偏移,分离区受到挤压。在主涡外侧,可以观察到二次分离线和再附线,说明此时已有较明显的二次涡产生。另一方面,由于机头前缘较尖,率先卷起一个小涡,在X/Cr=0.3处,由于前缘半径的急剧变化,涡的形态也明显改变,机头较尖的前缘起到了类似边条翼的作用效果。通过流线图和Q等值面(图 8)可以观察到自机头拖出的小涡汇入后面的主涡并互相缠绕在一起,同时,后缘外侧卷起一个与主涡旋转方向相反的小涡,在后缘翼稍处形成一个低压区,提供一部分升力。
 |
| 图 7 迎角12°时的流线和压力云图Fig. 7 Streamlines and Cp at α=12° |
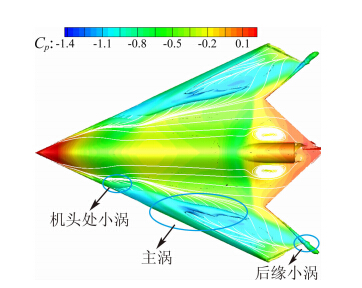 |
| 图 8 迎角12°时的Q=3等值面图Fig. 8 ISO-surface of Q=3 at α=12° |
图 9显示的是迎角12°时沿流向的密度梯度等值面,此时可以清晰观察到沿流向的两道激波,其中强度较大的激波依然位于X/Cr=0.7的位置。而较弱的第一道激波位于X/Cr=0.3处,正是这道激波的存在使得该处物面的深蓝色低压区被小部分高压带隔断。
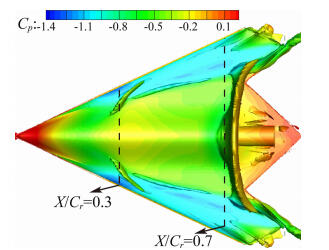 |
| 图 9 迎角12°时的密度梯度等值面Fig. 9 ISO-surface of density gradient α=12° |
总之,在跨声速范围内,随着激波的出现,前缘涡的结构与激波的位置和形态联系紧密,必须综合考虑二者的相互作用关系。 3.3 涡破裂现象
当迎角增大到某一临界值时,前缘涡在背风面发生破裂,且破裂位置会随迎角的增大突然向前移动,与此同时,激波位置也会突然前移,涡破裂的轴向位置与内侧激波出现的位置基本平齐,从图 10和图 11可以清晰观察到内侧激波后的黄色高压带,外侧涡破裂之后的区域压力也迅速升高,且在迎角12°时可以清晰观察到的后缘小涡此时也发生了显著变化,对机翼背风面已经几乎没有影响,正是机翼背风面压力的显著变化直接导致了全机升力突然下降并伴随俯仰力矩曲线突然上扬。
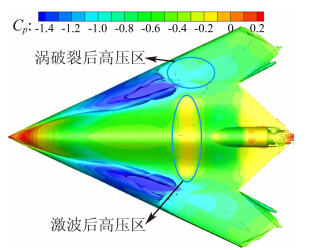 |
| 图 10 迎角20°时的Q=3等值面图Fig. 10 ISO-surface of Q=3 at α=20° |
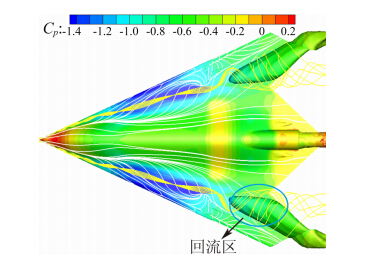 |
| 图 11 迎角20°时的流线和U=0等值面Fig. 11 Streamlines and ISO-surface of U=0 at α=20° |
图 11中绘制的轴向速度U=0的等值面清晰显示了涡破裂后出现的回流区域。图 12为迎角20°时沿流向的密度梯度等值面,可以发现,在涡破裂的位置,激波与前缘涡发生了较强的交叉干扰,此处有较明显的密度变化。
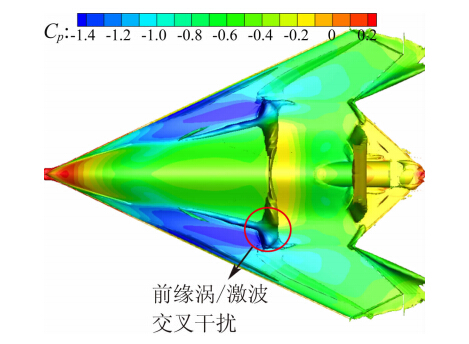 |
| 图 12 迎角20°时的密度梯度等值面Fig. 12 ISO-surface of density gradient α=20° |
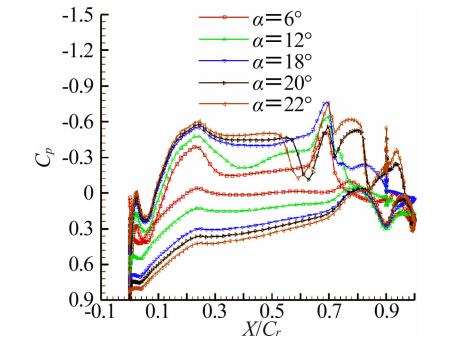 |
| 图 13 对称面压力系数分布Fig. 13 Cp distribution along streamwise at η=0 |
图 13和图 14分别选取了对称面和 η=0.3两个 展向位置在不同迎角时的表面压力系数进行对比。可以发现,迎角6°、12°和18°时,尚未达到临界迎角,三者的流态是类似的,顺着流向看,流场首先在机头处经历一道激波,绕过机头时,上表面压力系数迅速降低,然后在X/Cr=0.3附近经历一道较弱的激波,接下来是一段平台区,直到X/Cr=0.65附近流场再一次加速,压力下降,然后在X/Cr=0.7处遭遇一道较强的激波,压力迅速上升。当迎角超过临界迎角之后,其表面压力系数相比前几个迎角发生了质的变化。迎角20°时,X/Cr=0.56处出现了一道明显的激波,X/Cr=0.7处的激波相比之前的三个迎角则明显弱了很多,但是在X/Cr=0.8附近又产生了一 道激波,迎角22°时的流态与20°时的流态类似,只是 第一道激波的位置稍有前移。
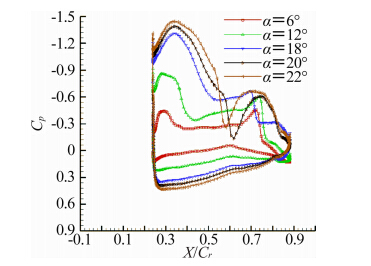 |
| 图 14 η=0.3处压力系数分布Fig. 14 Cp distribution along streamwise at η=0.3 |
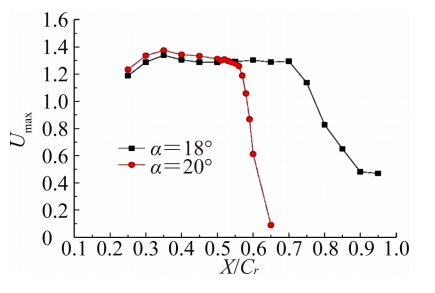
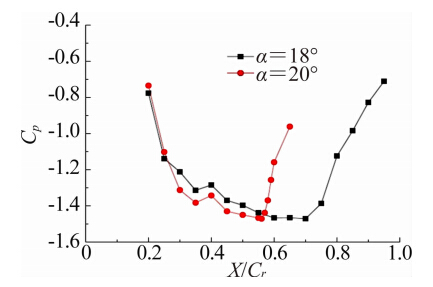
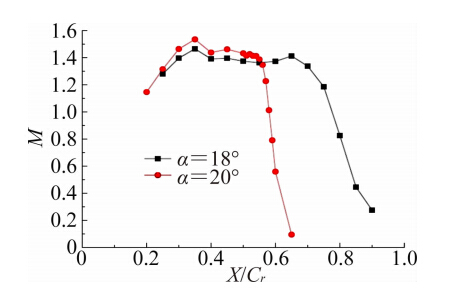
图 15选取了升力突降之前的迎角18°和升力突降之后的迎角20°的涡核区域轴向速度进行对比。图 16和图 17则是表示迎角18°和20°时涡核处的压力系数和马赫数分布情况。可以发现,在 X/Cr=0.4附近,涡核经历了一小段逆压区,依据前文的分析,此处应是经历了一道激波。对于迎角18°,涡核在经历X/Cr=0.4处的弱激波之后,一直保持着顺压梯度直到X/Cr=0.7 附近,轴向速度也直到X/Cr=0.7附近才出现下降,而迎角20°时,涡核在X/Cr=0.56附近遭受了较强的逆压梯度,轴向速度开始明显下滑,从图 17中还可以发现,在遭受强逆压梯度之前,涡核内的流速已经达到超声速,最大马赫数超过1.4。
 |
| 图 15 涡核轴向速度分布Fig. 15 U-velocity distribution through vortex cores |
 |
| 图 16 涡核压力系数分布Fig. 16 Cp distribution through vortex cores |
 |
| 图 17 涡核马赫数分布Fig. 17 Mach number distribution through vortex cores |
已有研究表明[15, 16, 17, 18],流向激波对涡的轴向速度影响较大而对周向速度影响较小,轴向速度降低后,涡的稳定性会降低直至破裂。
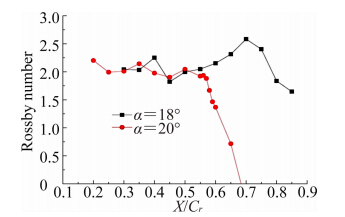
Rossby参数可用于衡量涡的稳定性,其基本定义如下:
上式中U表示涡核的轴向速度,Ur表示涡核的周向速度,Ro值越大表明涡越稳定。工程中获得Ro值的方法尚未统一,既有采用涡核区域最大轴向速度和最大周向速度相除的方法[17],也有采用平均速度的方法[19]。对于涡核区域的定义也不尽相同,Robinson[19]对65°平板三角翼研究时得出一个经验值,即取涡核中心距物面距离的20%作为涡核区域的半径可以得到较为理想的结论。
对小展弦比飞翼标模的分析实践中发现,受机身厚度变化和前缘半径变化等因素的影响,其前缘涡的形状相比平板三角翼更复杂,轴向速度并不相对涡轴周向对称。若采用最大速度的方法进行计算,则Ro值的大小对涡核区域的选取十分敏感,会引入较大误差,而采用平均值的方法则可靠性较高。另一方面,相对平板三角翼而言,小展弦比飞翼标模受前缘和机身厚度等因素的影响,其前缘涡离物面更近,若参照Robinson[19]的方法取涡核中心距物面距离的20%作为涡核区域的半径,则前缘涡的影响范围未能得到充分体现。经过多次尝试和折衷,最终选取涡核距物面长度的40%作为飞翼标模的涡核半径,得到的结果如图 18所示。从图 18可以看出,迎角18°时,在X/Cr =0.4附近,受弱激波的影响,前缘涡稳定度略有波 动,但并未发生破裂,X/Cr=0.45至X/Cr=0.7附 近,前缘涡的稳定度略有提升,结合前文的分析,涡核在这一段区域刚好经历了一段顺压梯度,因而前缘涡的稳定度得到提升也是合理的。迎角20°时,值在 X/Cr=0.56附近开始急剧下降,这意味着前缘涡已破裂。
 |
| 图 18 迎角18°和迎角20°时Rossby 参数对比Fig. 18 Rossby number at α=18° and α=20° |
通过数值模拟研究了小展弦比飞翼标模的跨声速典型气动特性,主要以涡升力为出发点,分析了涡的产生、发展直至破裂的整个过程,并着重解释了小展弦比飞翼标模风洞试验结果中跨声速升力突然下降的原因。
结果表明:马赫0.9时,飞翼标模在迎角4°开始出现涡升力;涡核内流动达到超声速,涡强随着迎角增加而增加,并向内侧移动,激波强度也逐渐增加,前缘涡与激波发生交叉干扰;当前缘涡与激波无法维持既有平衡时则会发生涡破裂,流场急剧变化以达到新的平衡,从而导致升力突然下降并产生抬头力矩增量。
| [1] | Roman D, Allen J B, Liebeck R H. Aerodynamic design challenges of the blended-wing-body subsonic transport[R]. AIAA 2000-4335. |
| [2] | William J G. Innovative control effect ors (configuration 101) dynamic wind tunnel test report[R]. AFRL-VA-WP-TR-1998-3043, 1998 |
| [3] | Wong M D, Flores J. Application of overflow-MLP to the design of the 1303 UCAV[R]. AIAA 2006-2987. |
| [4] | Rizzi A, Tomac M, Nangia R. Engineering methods for SACCON configuration[R]. AIAA 2010-4398. |
| [5] | Liu Xiaojing, Wu Jianghao, Zhang Shuguang. Aerodynamic design and optimization of the blended wingbody aircraft for 250 passengers[J]. Acta Aerodynamica Sinica, 2011, 29(1): 78-84.(in Chinese) 刘晓静, 吴江浩, 张曙光. 250座级翼身融合布局客机气动设计与优化[J]. 空气动力学学报, 2011, 29(1): 78-84. |
| [6] | Gong Junfeng, Zhu Xiaoping, Tao Yujin. Split drag rudder hinge moment predict for flying wing aircraft[J]. Acta Aerodynamica Sinica, 2010, 28(4): 472-477. (in Chinese) 龚军锋, 祝小平, 陶于金. 飞翼飞机开裂式阻力方向舵铰链力矩的预测[J]. 空气动力学学报, 2010, 28(4): 472-477. |
| [7] | Zuo Linxuan, Wang Jinjun. Experimental study of the effect of AMT on aerodynamic performance of tail less flying wing aircraft[J]. Acta Aerodynamica Sinica, 2010, 28(2): 132-137. (in Chinese) 左林玄, 王晋军. 全动翼尖对无尾飞翼布局飞机气动特性影响的实验研究[J]. 空气动力学学报, 2010, 28(2): 132-137. |
| [8] | Kong Yinan, He Kaifeng, Wang Lixin, et al. Simulation of flyingwing aircraft maneuver with leading edge jet control[J]. Acta Aerodynamica Sinica, 2013, 31(2): 186-191. (in Chinese) 孔轶男, 何开锋, 王立新, 等. 增加喷流控制的飞翼飞机机动仿真[J]. 空气动力学学报, 2013, 31(2): 186-191. |
| [9] | Chu J, Luckring J M. Experimental surface pressure data obtained on 65 deg delta wing across Reynolds number and Mach number ranges[R]. NASA 1996-4645. |
| [10] | Willy Pritz. Numerical simulation of the peculiar subsonic flow-field about the VFE-2 delta wing with rounded leading edge[R]. AIAA 2008-393. |
| [11] | Simone Crippa, Arthur Rizzi. Steady, subsonic CFD analysis of the VFE-2 configuration and comparison to wind tunnel data[R]. AIAA 2008-397. |
| [12] | Polhamus E C. Application of the leading-edge-suction analogy of vortex lift to the drag due to lift of sharp-edge delta wings[R]. NASA TN-D-4739, 1968. |
| [13] | Hunt J C R, Wray A A, Moin P. Eddies, streams, and convergence zones in turbulent flows[R]. N89-24555/9/XAD, 1989. |
| [14] | Marcel Lesieur. Large-eddy simulations of turbulence[M]. Cambridge UniversityPress, 2005. |
| [15] | Kalkhoran I M, Smart M K. Aspects of shock wave-induced vortex breakdown[J]. Progress in Aerospace Sciences, 2000, 36(1): 63-95. |
| [16] | Délery J M. Aspects of vortex breakdown[J]. Progress in Aerospace Sciences, 1994, 30(1): 1-59. |
| [17] | Schiavetta L A, Boelens O J, Crippa S. Shock effects on delta wing vortex breakdown[J]. Journal of Aircraft, 2009, 46(3): 903-914. |
| [18] | Visbal M R. Computational and physical aspectsof vortex breakdown on delta wing[R]. AIAA 95-0585. |
| [19] | Robinson B A, Barnett R M, Agrawal S. Simple numerical criterion for vortex breakdown[J]. AIAA Journal, 1994, 32(1): 116-122. |