0 引 言
飞翼布局因其具有优良的气动、结构和隐身性能而受到广泛关注,目前已有B-2远程轰炸机和X-47B、神经元无人作战飞机等飞翼布局代表作成功面世。此外,欧美国家还发布了多个飞翼布局通用研究模型用于飞翼布局基础理论研究,如ICE新型控制面模型[1]、UCAV1301/1302/1303系列[2]、SACCON通用研究模型[3]等。国内针对飞翼布局的开裂式方向舵、全动翼尖、喷流控制等若干问题开展了部分研究[4, 5, 6]。为了满足未来飞行器气动力试验与研究的需求,尤其考虑到超声速飞行的要求,国内有关机构自主设计了小展弦比飞翼标模,作为小展弦比融合体飞翼外形的通用研究平台,该小展弦比飞翼标模具有65°后掠角直前缘。对于类似布局前缘涡的研究也一直未停止[7, 8, 9, 10, 11]。
支撑干扰是一个由来已久的问题,国内外研究人员已经探索出许多研究方法并应用于工程实践,获得了一些有益的经验[12, 13, 14, 15, 16, 17, 18],但是对于小展弦比融合体飞翼布局类型飞行器的支撑干扰研究却较少见诸报道。飞翼布局相比常规布局不再有传统意义上的机身,其机身和机翼采用一体化设计。为了提高隐身性能,其发动机喷口通常也与机翼/机身一体化设计,不再有传统的圆形喷口,因此,在开展风洞试验时,风洞支撑系统不可避免会迫使其外形局部发生较大的改变,从而引入支撑干扰。为了获得更精准的试验数据,有必要对其支撑干扰进行研究。我们采用数值模拟方法对模型进行了计算分析,选取典型状态的计算结果与试验数据进行了对比,并着重研究了小展弦比飞翼标模在马赫数0.6、0.9、1.5时的支撑干扰特性。 1 数值模拟方法
针对小展弦比飞翼标模的三套网格进行了对比计算。三套网格分别为真实外形网格、仅考虑近场干扰(由于安装尾支杆而产生的尾部外形局部畸变和尾撑直支杆干扰)的网格和考虑远场干扰(增加风洞中部支架的影响)的网格。为了尽量减小网格的干扰,三套网格均采用OH型拓扑结构,仅在外形不同的尾部区域网格不一样,其他均保持一致。网格结构如图 1所示。网格远场距离物面的距离均大于模型全长的十倍。
数值求解采用的控制方程为雷诺平均N-S方程,空间离散方法为有限体积法,空间无粘通量采用ROE格式进行离散,粘性通量采用二阶中心差分格式离散,时间项采用隐式LU-SGS方法求解。为了加快收敛速度,还采用了局部时间步长和多重网格技术。湍流模型为k-ω SST二方程模型。物面采用无滑移边界条件,远场采用无反射边界条件,未考虑洞壁干扰,计算雷诺数与试验雷诺数保持一致。 2 典型计算结果与试验数据对比
图 2、图 3为马赫数0.9时纵向升力特性和俯仰力矩特性的计算结果与1.2米亚跨超声速风洞的试验结果(包含近场干扰和远场干扰)对比,可以发现,考虑远场风洞中部支架干扰的计算结果与试验结果最为接近。
 |
| 图 1 网格结构Fig. 1 Mesh scheme |
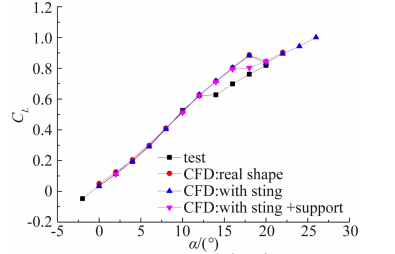 |
| 图 2 M=0.9升力系数Fig. 2 Lift coefficient at M=0.9 |
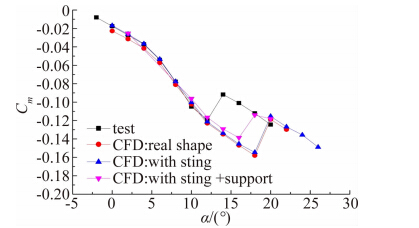 |
| 图 3 M=0.9俯仰力矩系数Fig. 3 Pitching moment coefficient at M=0.9 |
图 4为马赫数0.8时近场干扰量CFD计算结果与近场支撑干扰试验数据(文献尚未发表)的对比。从图 4可以看出,近场支撑干扰量的计算结果量值与近场支撑干扰试验数据相当,变化规律也基本一致,由此进一步验证了本文所采用的数值模拟方法可靠有效。
 |
| 图 4 M=0.8近场支撑干扰Fig. 4 Near field support interference at M=0.8 |
3 支撑干扰计算结果与分析 3.1 亚声速支撑干扰计算结果与分析
通过带支撑系统模型的气动力减去真实外形的气动力得到两个支撑干扰量,未考虑风洞中部支架的干扰量称为近场干扰量,考虑了风洞中部支架的干扰量为总干扰量(近场干扰与远场干扰之和)。
在亚声速范围内,选取马赫数0.6为典型马赫数,侧滑角为0°时的支撑干扰计算结果如图 5所示。从图 5中可以看出,在迎角小于15°的范围内,升力系数、阻力系数、俯仰力矩系数的近场干扰量均随迎角的增大而增大;进一步考虑远场的干扰之后,各气动力系数的支撑干扰总量随迎角的变化规律与近场干扰量的变化规律一致,干扰量值均有所增加。
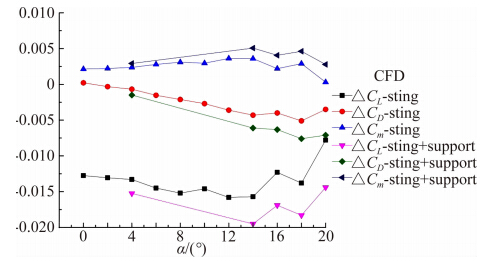 |
| 图 5 尾支杆、中部支架支撑对气动特性的干扰量(M=0.6)Fig. 5 Support interference at M=0.6 |
图 6与图 7显示了马赫数0.6、迎角4°时真实外形和试验带支杆外形的表面压力系数分布云图。从图中可以直观看到支撑干扰的影响。在全长的60%至80%处的内侧,真实外形由于有明显的尾部收缩变化,流场加速,压力降低,而试验带支杆外形由于收缩段受到破坏,此处的低压区大部分消失。正是由于试验外形尾部上表面压力增大,导致升力减小、阻力减小,并产生抬头力矩增量。
 |
| 图 6 真实外形压力系数分布(M=0.6,α=4°)Fig. 6 Cp of real shape at M=0.6,α=4° |
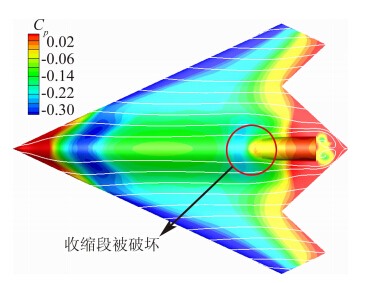 |
| 图 7 试验外形压力系数分布(M=0.6,α=4°)Fig. 7 Cp of test shape with sting at M=0.6,α=4° |
表 1列出了马赫数0.6、迎角14°时的升力系数、阻力系数和俯仰力矩系数的详细值。从表 1中可以看出,未考虑中部支架影响时的支撑干扰量均偏小。对于升力系数而言,考虑中部支架的影响后,支撑干扰量由-0.0157变为-0.0195,干扰量占总量的百分比由2.4%提高到3.0%;对于阻力系数而言,支撑干扰量由-0.0043变为-0.0061,干扰量占总量的百分比由2.8%提高到4.1%;对于俯仰力矩系数而言,支撑干扰量由0.0036变为0.0051,干扰量占总量的百分比由3.6%提高到5.3%。
| 真实外形 | 考虑近场 | 考虑近场加远场 | |
| CL | 0.6665 | 0.6508 | 0.6470 |
| CD | 0.1543 | 0.1500 | 0.1482 |
| Cm | -0.0994 | -0.0958 | -0.0943 |
| ΔCL | / | -0.0157 | -0.0195 |
| ΔCD | / | -0.0043 | -0.0061 |
| ΔCm | / | 0.0036 | 0.0051 |
从占总量的百分比考虑,支杆和中部支架对俯仰力矩系数的影响最大,阻力系数次之,对升力系数的影响最小。如果把支杆加中部支架引起的支撑干扰量当做总支撑干扰量,那么由尾部直支杆导致的支撑干扰量所占的比例分别为80.5%、70.5%和71.0%。由此可见,模型尾部收缩段被破坏和尾撑直支杆的存在依然是造成支撑干扰的主要原因,但中部支架的影响量也不能忽略,中部支架对阻力系数和俯仰力矩系数的影响比对升力系数的影响较明显。
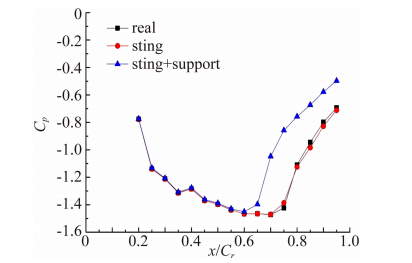
图 8对比了马赫数0.6、迎角14°时三个外形的X/Cr=0.7站位展向截面的压力系数,图中real表示真实外形,sting表示仅考虑近场支撑干扰的外形,sting+support表示考虑了近场和远场支撑干扰的外形。可以看出,受支杆和尾部收缩段破坏的影响,上表面的压力系数均有所增大,由前缘涡引起的吸力峰负压有所降低,但是吸力峰出现的位置基本不受影响,且机翼下表面所受影响也几乎可以忽略。随着中部支架的加入后,上表面的压力系数进一步增高,吸力峰出现的位置依然未变,但是与尾撑直支杆的影响规律不一样的是此时下表面的压力系数也有所增加。
 |
| 图 8 X/Cr=0.7站位处展向压力系数(M=0.6,α=14°)Fig. 8 Pressure coefficience at X/Cr=0.7,M=0.6,α=14° |
图 9对比了马赫数0.6、迎角14°时三个外形在η=0.3站位流向截面的压力系数,可以看出,支撑干 扰最明显的地方位于X/Cr=0.7附近,干扰会前传 至X/Cr=0.5之前,中部支架的影响会使得上下表面的压力均有所升高。
 |
| 图 9 η=0.3流向截面马赫数0.6、迎角14°流向压力系数Fig. 9 Pressure coefficience at η=0.3,M=0.6,α=14° |
在跨声速范围内,选取马赫数0.9为典型马赫数,侧滑角为0°时的支撑干扰结果如图 10所示,可以发现在 迎角小于12°的范围内,升力系数和俯仰力矩系数的近场干扰量随迎角的增大而减小,而阻力系数的支撑干扰量在计算范围内随迎角增大而减小,考虑远场干扰之后,各气动力系数的支撑干扰量均有所增大。
 |
| 图 10 马赫数0.9支撑干扰量Fig. 10 Support interference at M=0.9 |
图 11与图 12显示的是马赫数0.9、迎角2°时真实外形和考虑近场干扰的两个外形的表面压力系数分布。从图中可以看出,类似于马赫数0.6时的情形,试验外形尾部收缩段破坏后,加速区面积减少。与马赫数0.6不同的是此处已经出现了激波,支撑干扰使得激波位置前移,因而波后高压区的面积也增加。激波前低压区减少加上波后高压区增大使得升力减小、阻力减小并产生抬头力矩增量。
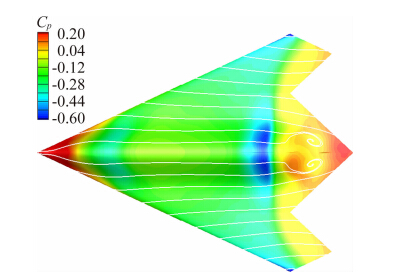 |
| 图 11 真实外形马赫数0.9、迎角2°压力系数分布Fig. 11 Cp of real shape at M=0.9,α=2° |
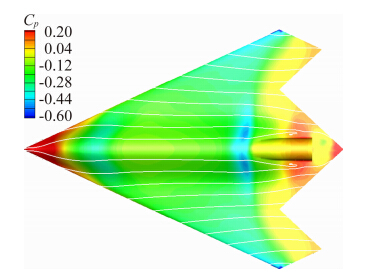 |
| 图 12 考虑近场干扰马赫数0.9、迎角2°压力系数分布Fig. 12 Cp of test shape with sting at M=0.9,α=2° |
图 13显示了马赫数0.9、迎角2°时真实外形和考虑近场干扰两个外形在对称面和η=0.3站位流向截面上的压力分布,可以看出支撑干扰明显使得激波位置前移。当迎角增加到10°时,如图 14所示,激波位置受支撑干扰的影响反而不如小迎角时明显,这解释了为什么马赫数0.9时,随着迎角增大,升力和俯仰力矩差量逐渐减小。
 |
| 图 13 马赫数0.9、迎角2°流向压力系数对比Fig. 13 Cp at η=0 and η=0.3(M=0.9,α=2°) |
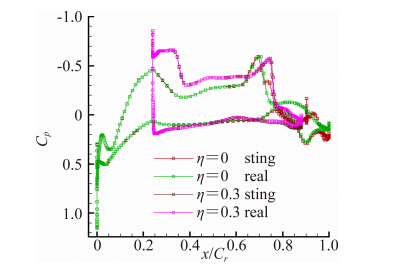 |
| 图 14 马赫数0.9、迎角10°流向压力系数对比Fig. 14 Cp at η=0 and η=0.3(M=0.9,α=10°) |
表 2列出了马赫数0.9、迎角2°时的升力系数、阻力系数和俯仰力矩系数的详细值。从表中可以看出,考虑中部支架的影响后,升力系数支撑干扰量由-0.0134变为-0.0152,阻力系数支撑干扰量由-0.0013变为-0.0022,俯仰力矩系数支撑干扰量由0.0053变为0.0062。支杆和尾部收缩段变形引起的升力系数 支撑干扰量占总升力系数支撑干扰量的88%,阻力 系数和俯仰力矩系数则分别对应59%和85%。由此可见,迎角2°时的升力系数和俯仰力矩系数支撑干扰量主要来源于支杆和尾部收缩段破坏,而阻力系数 则受中部支架的影响也比较明显。
| 真实外形 | 带支杆外形 | 带支杆加中部支架 | |
| CL | 0.1262 | 0.1128 | 0.1110 |
| CD | 0.0122 | 0.0109 | 0.0100 |
| Cm | -0.0315 | -0.0262 | -0.0253 |
| ΔCL | / | -0.0134 | -0.0152 |
| ΔCD | / | -0.0013 | -0.0022 |
| ΔCm | / | 0.0053 | 0.0062 |
迎角18°时,由于此迎角已经接近涡破裂的临界迎角,支撑干扰能使流场结构发生质的改变。图 15和图 16为有无中部支架对称面的马赫数的对比,图 17为涡核内压力系数的对比。可以发现,当加入中部支架的干扰之后,激波形态发生明显改变,涡破裂位置迅速前移,导致升力下降、俯仰力矩曲线上扬。
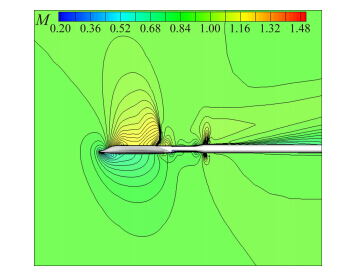 |
| 图 15 无远场干扰对称面马赫数分布(M=0.9,α=18°)Fig. 15 M of test shape with sting at M=0.9,α=18° |
 |
| 图 16 有远场干扰对称面马赫数分布(M=0.9,α=18°)Fig. 16 Test shape with sting and support at M=0.9,α=18° |
 |
| 图 17 马赫数0.9、迎角18°涡核压力系数Fig. 17 Cp of vortex center at M=0.9,α=18° |
3.3 超声速支撑干扰算结果与分析
在超声速范围内,选择马赫1.5为典型马赫数,由于超声速区域干扰无法前传,因而中部支架的干扰几乎可以忽略,对比结果如图 18所示。
 |
| 图 18 马赫1.5有无中部支架支撑干扰量对比Fig. 18 Support interference at M=1.5 |
4 近场支撑干扰分解分析
近年来,不断提高的型号研发需求对风洞试验中各种干扰量的扣除要求越来越精细。本文参照法国Aurélia Cartieri1[18]等在研究一类运输机外形时的做法,对小展弦比飞翼标模近场支撑干扰量进行分解分析。
风洞支架对模型附近流场的干扰主要体现在两个方面,即支杆的存在改变了模型附近的马赫数和模型实际迎角。从物理意义上来理解就是支杆的阻塞作用改变了模型附近的马赫数,支杆对流场的扰动又会产生上洗或者下洗,因而改变了模型的实际迎角。
研究的具体操作方法是:考虑两种情形,其一为无支杆的真实模型,设其远场来流条件为马赫数等于M,迎角等于α,由于没有支杆的存在,模型附近的流场也是马赫数等于M,迎角等于α;其二为模型加支杆的情形,设其远场来流条件为马赫数等于M′,迎角等于α′,由于支杆的存在,模型附近的流场变为马赫数等于M′+ΔM,迎角等于α′+Δα。我们的目的是要对比这两种情形,改变有支杆时的远场来流M′和α′,让有支杆时模型附近的流场与无支杆时模型附近的流场最为接近,即使得M′+ΔM=M,α′+Δα=α。本文以表面压力系数差异为准则,其表达式如下:
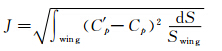
对于本文所讨论的小展弦比飞翼标模,由于其试验外形破坏的是尾部上表面收缩段,尾支杆也离上表面更近,因而选择上表面外侧作为由压力系数计算压力系数差的参考面,其具体范围如图 19所示。
 |
| 图 19 计算压力系数差异所选用的参考表面Fig. 19 Reference area |
实践过程中发现,对于飞翼标模,由于其尾部放大破坏面积较大,在马赫数0.6、迎角4°时,扰动前传比较明显,导致计算所得压力系数差异在很大马赫数范围内一直单调递减,直到试验外形远场来流M=0.72时压力系数差才达到极小值,即支撑干扰马赫数影响量达到了0.12左右,这显然是不合理的。进一步研究发现,真实外形在M=0.6、迎角4°时的参考表面压力分布与试验外形在M=0.72、迎角4°时的参考表面压力分布确实更接近。究其原因,主要是由于飞翼标模试验外形尾部破坏较大,在低马赫数情况下,扰动前传比较明显,且由于马赫数较低,没有激波的存在,此时压力分布对马赫数不是特别敏感,因此导致了试验外形M=0.72时的参考表面压力分布碰巧与真实外形M=0.6时的参考表面压力分布具有很高的相似度,但是把这马赫数0.12的差量当成是支撑干扰量明显是不合适的,此时表面压力系数差取到极小值只能说明二者的压力分布情况十分接近。
对于跨声速情形,本文选择马赫数0.9、迎角2°进行了研究。马赫数0.9相比于马赫数0.6时一个很大的不同之处在于激波的出现,而激波的出现使得压力系数差对马赫数和迎角变得更敏感,因而此时用此法可以成功将支撑干扰量分解为对马赫数的影响和对迎角的影响。对若干离散的计算点经过二次函 数拟合得到近似的压力系数差分布云图如图 20所示,从图 20中可以看出,压力系数差对于马赫数的变化十分敏感,极小值出现在ΔM=0.02、Δα=0.1附近,即表示试验外形在马赫数0.92、迎角2.1°附近与真实外形马赫数0.9、迎角2°时表面压力系数分布最为接近。
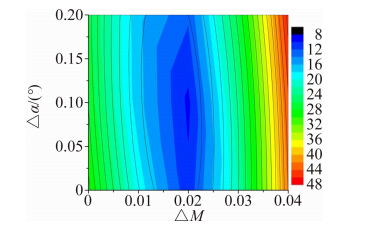 |
| 图 20 马赫数0.9、迎角2°时的压力系数差云图Fig. 20 ΔM vs. Δα at M=0.9,α=2° |
在风洞试验数据与CFD计算结果对比的基础上,用数值模拟方法研究了小展弦比飞翼标模在0.6、0.9、1.5三个典型马赫数下的支撑干扰特性,分别考虑了近场干扰和远场干扰,并基于表面压力系数差异为准则尝试对近场干扰量进行分解,得到有如下结论:
(1) 亚声速马赫数0.6时,阻力系数和俯仰力矩系数的远场支撑干扰量约占总支撑干扰量的30%,升力系数约占20%。
(2) 马赫数0.9、迎角2°时,阻力系数远场支撑干扰量占总支撑干扰量的40%,近场干扰使得激波位置前移,激波强度降低,远场干扰使激波位置进一步前移,强度进一步降低;近场干扰主要影响上表面的压力,而远场干扰则会同时使得上下表面的压力都升高,相比升力系数和俯仰力矩系数,阻力系数受远场干扰的影响更明显;迎角18°时,远场支撑干扰使得涡破裂位置前移,导致流场结构发生剧变。
(3) 超声速马赫数1.5时,远场支撑干扰可以忽略。
(4) 基于表面压力系数差异将支撑干扰量分解的方法在亚声速支撑干扰前传明显时不适用,在马赫数0.9、迎角2°时求得近场支撑干扰使得马赫数减小约0.02,迎角减小约0.1°,马赫数1.5时用此法求得马赫数和迎角的干扰量均约等于0。
| [1] | William J G. Innovative control effect ors (configuration 101) dynamic wind tunnel test report[R]. AFRL-VA-WP-TR-1998-3043, 1998. |
| [2] | Wong M D, Flores J. Application of OVERFLOW-MLP to the design of the 1303 UCAV[R]. AIAA 2006-2987. |
| [3] | Rizzi A, Tomac M, Nangia R. Engineering methods for SACCON configuration[R]. AIAA 2010-4398. |
| [4] | Kong Yinan, He Kaifeng, Wang Lixin, et al. Simulation of flying wing aircraft maneuver with leading edge jet control[J]. Acta Aerodynamica Sinica, 2013, 31(2): 186-191. (in Chinese) 孔轶男, 何开锋, 王立新, 等. 增加喷流控制的飞翼飞机机动仿真[J]. 空气动力学学报, 2013, 31(2): 186-191. |
| [5] | Gong Junfeng, Zhu Xiaoping, Tao Yujin. Split drag rudder hinge moment predict for flying wing aircraft[J]. Acta Aerodynamica Sinica, 2010, 28(4): 472-477.(in Chinese) 龚军锋, 祝小平, 陶于金. 飞翼飞机开裂式阻力方向舵铰链力矩的预测[J]. 空气动力学学报, 2010, 28(4): 472-477. |
| [6] | Zuo Linxuan, Wang Jinjun. Experimental study of the effect of AMT on aerodynamicperformance of tail less flying wing aircraft[J]. Acta Aerodynamica Sinica, 2010, 28(2): 132-137. (in Chinese) 左林玄, 王晋军. 全动翼尖对无尾飞翼布局飞机气动特性影响的实验研究[J]. 空气动力学学报, 2010, 28(2): 132-137. |
| [7] | Willy Pritz. Numerical simulation of the peculiar subsonic flow-field about the VFE-2 delta wing with rounded leading edge.[R]. AIAA 2008-393. |
| [8] | Simone Crippa, Arthur Rizzi. Steady, subsonic CFD analysis of the VFE-2 configuration and comparison to wind tunnel data.[R]. AIAA 2008-397. |
| [9] | Russell M Cummings, Andreas Schütte. Detached-eddy simulation of thevertical flow field about the VFE-2 delta wing[R]. AIAA 2008-396. |
| [10] | Kalkhoran I M, Smart M K. Aspects of shock wave-induced vortex breakdown[J]. Progress in Aerospace Sciences, 2000, 36(1): 63-95. |
| [11] | Schiavetta L A, Boelens O J, Crippa S. Shock effects on delta wing vortex breakdown[J]. Journal of Aircraft, 2009, 46(3): 903-915. |
| [12] | 崔乃明. 高速风洞洞壁干扰和支架干扰的工程修正方法[J]. 航空学报, 1990, 11(12): 523-527. Cui Naiming. An engineering correction method for tunnel wall interference and sting-support interference in high speed wind tunnels[J]. Acta Aeronautica et Astronautica Sinica, 1990, 11(12): 523-527. |
| [13] | 范召林, 尹陆平, 崔乃明. 高速风洞腹部支架干扰工程计算方法[J]. 气动实验与测量控制, 1994, 8(2): 71-77. Fan Zhaolin, Cui Naiming, Yin Lupin, et al. An engineering method for computing ventral strut interference on models in high speed wind tunnel tests[J]. Aerodynamic Experiment and Measurement & Control, 1994, 8(2): 71-77. |
| [14] | 贺中, 范召林, 吴军强, 等. 尾支杆干扰非线性修正方法的初步研究[J]. 流体力学实验与测量, 2001, 15(1): 26-31. He Zhong, Fan Zhaolin, Wu Junqiang, et al. Preliminary research on non-linnear correction method of sting interference[J]. Experiment and Measurements in Fluid Mechanics, 2001, 15(1): 26-31. |
| [15] | 杨立芝, 李俊甫, 董军. 高速风洞支架干扰数值修正研究[J]. 流体力学实验与测量, 2001, 15(3): 84-88. Yang Lizhi, Li Junfu, Dong Jun. Computational investigation of longitudinal support interferences in high speed wind tunnel[J]. Experiment and Measurements in Fluid Mechanics, 2001, 15(3): 84-88. |
| [16] | 段卓毅, 王运涛, 庞宇飞, 等. 无尾布局支撑干扰数值模拟[J]. 实验流体力学, 2007, 21(4): 13-17. Duan Zhuoyi, Wang Yuntao, Pang Yufei, et al. Numerical simulationof support interference on a tail less configuration[J]. Journal of Experiments in Fluid Mechanics, 2007, 21(4): 13-17. |
| [17] | 周林, 董建鸿, 李苗苗. 高速风洞试验中运输机支撑形式的选择[J]. 航空工程进展, 2012, 3(1): 33-38. Zhou Lin, Dong Jianhong, Li Miaomiao. Choice of support form for transport aircraft in high speed wind tunnel test[J]. Advances in Aeronautical Science and Engineering, 2012, 3(1): 33-38. |
| [18] | Aurélia Cartieri, Sylvain Mouton. Using CFD to calculate support interference effects[C]. AIAA, 2012. |


