0 引 言
小展弦比飞翼标模外形研究是“风洞试验技术”联合攻关课题的基本切入点和重要研究载体。该项目重点针对先进飞机气动力试验研究的需求,以小展弦 比融合体飞翼布局标模为载体,在全国范围内开展相 关的气动力风洞试验技术联合攻关。
尽管世界各航空航天大国一直致力于建造大口径或高雷诺数风洞,但迄今为止,风洞试验雷诺数仍比真实飞行雷诺数低1~2个数量级,使得风洞测量的气动数据与实际飞行条件中的气动数据存在一定的差别。所以自风洞发展建设百余年以来,风洞试验结果外推到飞行条件时的雷诺数影响修正问题,或者说风洞缩尺模型试验结果的外推问题一直是飞行器设计人员关心的焦点问题[1]。已经有相当多的文章涉及到这个问题,也不乏一些总结性文章。北大西洋公约组织流体力学小组曾专门召开会议讨论,发表了一些总结性和指导性专集[2, 3, 4, 5, 6, 7],这些专集文章涉及到风洞试结果的外推和雷诺数影响,文章中涉及到了大部分已知的飞机(包括波音和空客的飞机以及一些战斗机)的风洞和飞行试验数据,这些数据和文献对于分析雷诺数影响有较大的参考价值。2006年,美国NASA兰利中心的Dennis M Bushnell还在《流体力学进展评述》中发表了《缩尺:从风洞到飞行》的文章[8],概括地总结了迄今有关这个问题的研究进展。
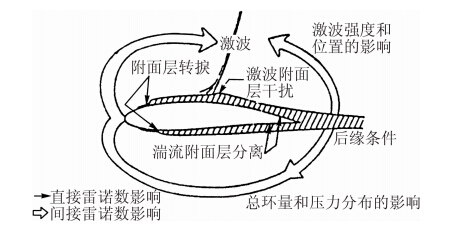 |
| 图 1 雷诺数对流动的影响Fig. 1 Effects of Reynolds number on flow characteristics |
雷诺数影响是一个很复杂的问题,它涉及层流、转捩、湍流、旋涡和分离等基本流动现象,要想完全搞清楚它们的影响是十分困难的。雷诺数不同,通常会对边界层类型、转捩点位置、边界层内速度分布形态、物体上分离点位置、分离形态和分离区大小,以及激波位置、边界层厚度等产生影响(如图 1[9]),从而导致飞行器气动特性的变化,进而影响到飞机性能和操稳特性。因此在使用缩比模型低雷诺数风洞试验数据时必须进行雷诺数影响修正。而CFD技术的发展已经可以为进行这样的修正提供必要的参考。
对于小展弦比机翼,特别是尖前缘情况,由于前缘分离点的位置比较固定,因而雷诺数的影响相对要小一些,雷诺数最直接的影响是二次分离的位置。而对于钝前缘机翼,雷诺数影响却很明显,并且可能持续到相当高的雷诺数,不同雷诺数时前缘分离位置、再附线的位置和压力分布形态都有很大的差别。
为了考察小展弦比飞翼标模的雷诺数影响问题,本文采用数值模拟方法分别计算了三个不同雷诺数条件下小展弦比飞翼标模的流场,分析了气动特性和流场特性随雷诺数变化的规律,为小展弦比飞翼标模风洞试验结果的雷诺数修正提供依据,并进一步促进雷诺数影响的相关性分析工作。 1 计算程序介绍
计算采用CARDC自主研制的亚跨超声速流场解算器Mbflow6.0进行。Mbflow6.0是基于多块对接结构网格技术的大规模并行CFD程序,适用于飞行器亚跨超声速气动特性和气动载荷计算,经过大量标准算 例[10, 11]的考核,在众多大型航空航天工程项目中得到广泛应用。程序控制方程采用非定常雷诺平均Navier-Stokes方程,湍流模 拟使用Spalart-Allmaras一方程湍流模型[12]或者SST两方程湍流模型[13]。采用基于格心的有限体积法离散,对流项采用Roe通量差分分裂格式或Van Leer矢通量分裂格式,粘性项采用中心格式离散,时间离散采用显式Runge-Kutta方法或隐式LU-SGS方法。采用基于MPI的大规模并行计算技术、多重网格方法、低速预处理技术和当地时间步方法等,从多方面提高流场计算的效率。网格输入和流场输出采用PLOT3D格式。程序可计算马赫数范围:0.001~20,攻角范围:-90°~90°,侧滑角范围:-90°~90°。
为了精细模拟雷诺数的影响,在本文的计算中,对流项采用目前应用非常广泛、边界层模拟精度高、激波分辨率好的Roe格式进行离散。时间项采用隐式LU-SGS方法。湍流模拟采用工程应用广泛、鲁棒性高的SA一方程湍流模型。在本文的计算状态下,雷诺数均比较大,在非常靠近机翼前缘的位置就实现转捩,转捩对整体气动特性的影响较小,因此在计算中采用全湍流模拟,不考虑转捩的影响。 2 计算模型及网格
计算外形为小展弦比飞翼标模的真实后体模型,如图 2所示。
 |
| 图 2 计算外形Fig. 2 Computational geometry |
网格生成技术是数值模拟的基础,首先按照给定的数模文件,生成表面计算网格。为使网格既满足附面层模拟的要求,又能很好地模拟飞机复杂外形,计算网格采用“三层次”的网格生成思想[14, 15],即靠近物面的第一层次主要模拟粘性附面层,中间的第二层次主要模拟空间的旋涡,靠近远场的第三层次主要是满足远场边界条件。根据全机的外形特点,采用分块对接网格,整个计算区域被分成若干个由六个曲面所围成的子区域,每一个子区域网格单独生成,但在每个子区域连接面处网格完全对接。每一个子区域网格采用无穷插值方法生成计算网格,用椭圆方程优化。
为了减小数值计算的网格相关性,本文所有计算采用同一套网格。为了满足准确模拟湍流附面层的要求[16],基于Ma=0.8、飞行雷诺数、y+≈1进行网格生成,法向第一层网格间距取为4.7×10-6 m,从而在本文计算的所有状态下y+都满足O(1)。法向网格的增长率取为1.2。
图 3是表面和对称面网格及拓扑结构示意图。采用“O”型网格拓扑[17],计算区域大小取为平均气动弦长的50倍。其中,流向网格点数为169,展向为173,法向为113,机翼后缘为17,半机总网格量约为739万。
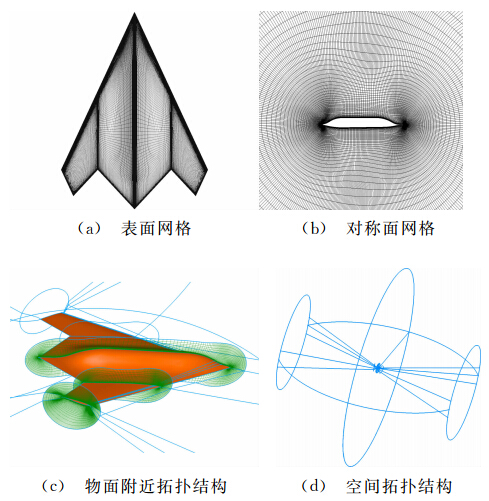 |
| 图 3 表面和对称面网格以及拓扑结构Fig. 3 Wall and symmetry surface grid and grid topology |
根据风洞试验条件,分别选取了低速、跨声速和超声速三个不同马赫数进行计算,具体计算状态如表 1所示。每个状态计算了三个不同的雷诺数:试验雷诺数、二倍试验雷诺数和飞行雷诺数,具体如表 2所示,其中Reexp表示试验雷诺数,2Reexp表示二倍试验雷诺数,Refly表示飞行雷诺数。
| case1,Reexp/106 | case2,2Reexp/106 | case3,Refly/106 | |
| Ma=0.2 | 4.0 | 8.0 | 44.5 |
| Ma=0.8 | 7.95 | 15.9 | 65.0 |
| Ma=1.5 | 11.0 | 22.0 | 121.8 |
图 4~图 6分别是Ma=0.2、0.8和1.5时气动特性的雷诺数影响曲线。总体来说,雷诺数对升力系数曲线、阻力系数曲线和俯仰力矩系数曲线影响较小,雷诺数对最大升阻比有一定影响。
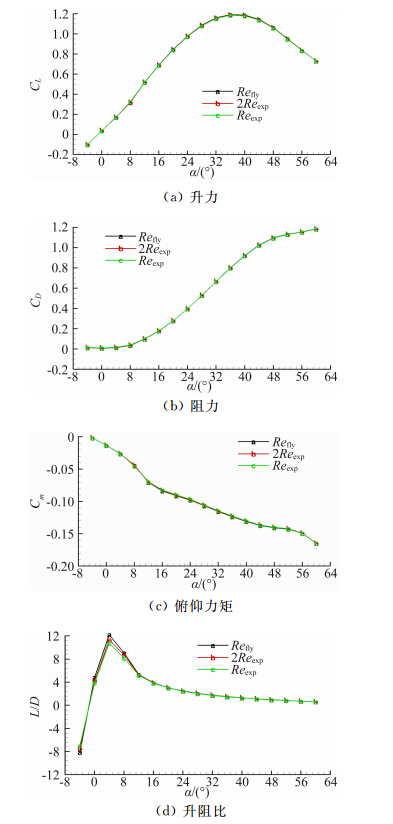 |
| 图 4 雷诺数对气动特性的影响(Ma=0.2)Fig. 4 Effects of Reynolds number on aerodynamic characteristics (Ma=0.2) |
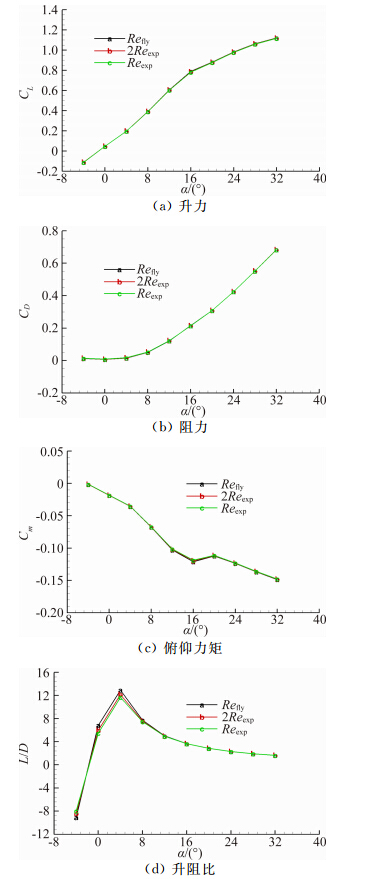 |
| 图 5 雷诺数对气动特性的影响(Ma=0.8)Fig. 5 Effects of Reynolds number on aerodynamic characteristics (Ma=0.8) |
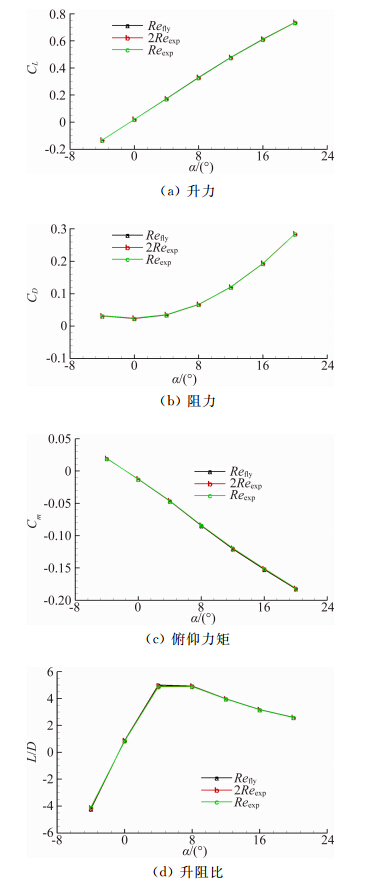 |
| 图 6 雷诺数对气动特性的影响(Ma=1.5)Fig. 6 Effects of Reynolds number on aerodynamic characteristics (Ma=1.5) |
表 3和表 4分别是Ma=0.2,α=4°和α=36°时 雷诺数对气动系数的影响,其中CD,p表示压差阻力系数,CD,v表示摩擦阻力系数,L/D表示升阻比。α=4° 时,标模的升阻比最大。由表 3可见,随着雷诺数增大,升力系数略有增大,阻力系数明显减小,从case1到case3,阻力系数减小了约17个cts(cts:阻力系数单位,1cts=0.0001),减小了约11.1%,其中主要是摩阻减小,压阻几乎不变;进而引起升阻比的增大。随着雷诺数增大,低头力矩略有增大。
| 状态 | CL | CD | CD,p | CD,v | Cm | L/D |
| case1 | 0.16961 | 0.01572 | 0.00812 | 0.00760 | -0.02584 | 10.79 |
| case2 | 0.17004 | 0.01504 | 0.00805 | 0.00699 | -0.02597 | 11.31 |
| case3 | 0.17075 | 0.01398 | 0.00798 | 0.00600 | -0.02617 | 12.21 |
| 状态 | CL | CD | CD,p | CD,v | Cm | L/D |
| case1 | 1.18616 | 0.79911 | 0.79273 | 0.00638 | -0.12264 | 1.484 |
| case2 | 1.18839 | 0.79912 | 0.79324 | 0.00588 | -0.12311 | 1.487 |
| case3 | 1.19257 | 0.80056 | 0.79541 | 0.00515 | -0.12366 | 1.490 |
α=36°时标模具有最大升力系数,随着雷诺数的增大,升力系数约有0.5%的增大,阻力系数也略有 增大,从而升阻比基本不变。从表 4可见,阻力系数 的增大是由压阻引起的,压阻增大了约27个cts,与小攻角情况相同,从case1到case3,摩阻减小了约12个cts;低头力矩约有0.8%的增大。
表 5和表 6分别是Ma=0.8,α=4°和α=16°时雷诺数对气动系数的影响。α=4°时,从case1到 case3,随雷诺数增大,升力系数约有0.8%的增大;阻力系数约减少了15个cts,其中主要是摩阻的减小,压阻变化非常小;从而升阻比增加了1.2;低头力矩系数约有1.2%的增大。α=16°时,从case1到 case3,随雷诺数增大,升力系数约有0.9%的增大;阻 力系数变化非常小,增加了3个cts,其中压阻增加了 16个cts,摩阻减小了13个cts;从而升阻比几乎不变;低头力矩系数约有2.0%的增大。
| 状态 | CL | CD | CD,p | CD,v | Cm | L/D |
| case1 | 0.19642 | 0.01682 | 0.01064 | 0.00618 | -0.03518 | 11.7 |
| case2 | 0.19714 | 0.01623 | 0.01058 | 0.00565 | -0.03537 | 12.1 |
| case3 | 0.19806 | 0.01534 | 0.01049 | 0.00485 | -0.03561 | 12.9 |
| 状态 | CL | CD | CD,p | CD,v | Cm | L/D |
| case1 | 0.78160 | 0.21469 | 0.20880 | 0.00589 | -0.11878 | 3.64 |
| case2 | 0.78463 | 0.21484 | 0.20949 | 0.00536 | -0.11978 | 3.65 |
| case3 | 0.78889 | 0.21501 | 0.21045 | 0.00456 | -0.12113 | 3.67 |
表 7和表 8分别是Ma=1.5,α=4°和α=20°时雷诺数对气动系数的影响。α=4°时,从case1到case3,升力系数增加了0.8%,阻力系数减小了约6个cts,其中摩阻减小了约11个cts,压阻增加了约5 个cts;升阻比增加了0.13;低头力矩系数增加了 1.5%。α=20°时,从case1到case3,升力系数增加了0.3%,阻力系数减小了约1个cts,其中摩阻减小了约9个cts,压阻增加了约7个cts;升阻比基本没有变化;低头力矩系数增加了约0.7%。
| 状态 | CL | CD | CD,p | CD,v | Cm | L/D |
| case1 | 0.17207 | 0.03533 | 0.03013 | 0.00520 | -0.04576 | 4.87 |
| case2 | 0.17260 | 0.03504 | 0.03030 | 0.00474 | -0.04604 | 4.93 |
| case3 | 0.17343 | 0.03470 | 0.03059 | 0.00411 | -0.04643 | 5.00 |
| 状态 | CL | CD | CD,p | CD,v | Cm | L/D |
| case1 | 0.73526 | 0.28486 | 0.28078 | 0.00408 | -0.18120 | 2.58 |
| case2 | 0.73623 | 0.28479 | 0.28108 | 0.00371 | -0.18173 | 2.59 |
| case3 | 0.73756 | 0.28473 | 0.28150 | 0.00323 | -0.18239 | 2.59 |
图 7是剖面的站位图。图 8和图 9是Ma=0.2,α=4°和α=16°时x/LB=20%、40%、60%和80%剖面雷诺数对压力分布的影响比较,其中LB表示机长。α=4°时,雷诺数只对80%站位上翼面内侧(即机尾附近)略有影响。雷诺数增大,使上翼面压力减小, 从而上下翼面压差增大,引起升力的增加,又因为80%位于力矩参考点之后,因此引起低头力矩的增加。雷诺数对其他剖面几乎没有影响。α=16°时,在20%站位之前就已经出现前缘涡分离;雷诺数对分离涡的位置有一定影响,相同的站位,雷诺数越大,分离涡越靠近前缘。
 |
| 图 7 剖面站位Fig. 7 Locations of section |
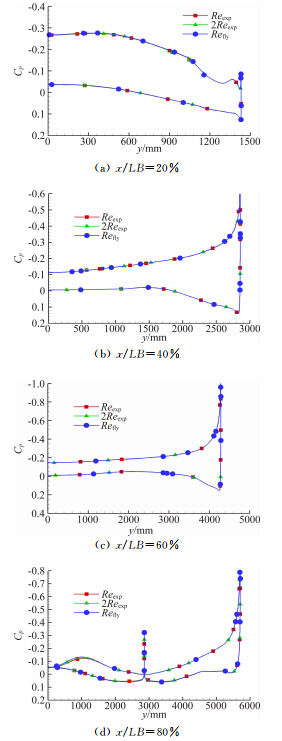 |
| 图 8 压力分布比较(Ma=0.2,α=4°)Fig. 8 Comparison of pressure distribution(Ma=0.2,α=4°) |
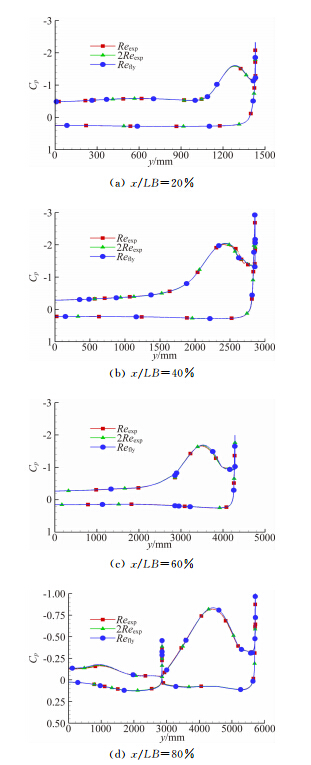 |
| 图 9 压力分布比较(Ma=0.2,α=16°)Fig. 9 Comparison of pressure distribution (Ma=0.2,α=16°) |
在小攻角附着流情况下,雷诺数主要影响摩擦阻力、边界层厚度和激波边界层干扰。雷诺数越大,粘性影响越小,从而摩擦阻力越小。对边界层厚度来说,越接近机翼后缘,不同雷诺数下的边界层位移厚度差别越大,对正弯度来说加厚的边界层是使“有效”弯度减小。因此,在正攻角,雷诺数大时,边界层较薄(如图 10),使机翼的“有效”弯度比雷诺数低时的“有效”弯度要大,从而升力增加。
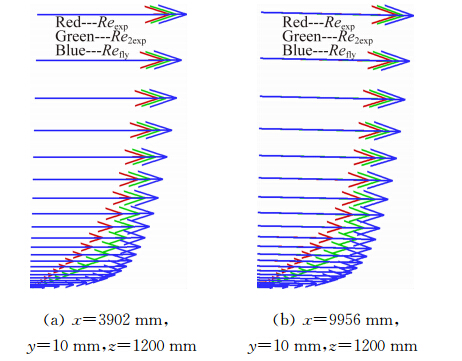 |
| 图 10 边界层内速度型比较(Ma=0.2,α=4°)Fig. 10 Comparison of velocity profile within boundary layer(Ma=0.2,α=4°) |
在大攻角情况下,对于尖前缘三角翼来说,雷诺数影响较小,最直接的影响是二次分离的位置,而二次分离位置的改变会影响到主涡的强度。随着雷诺数增加,引起从层流到湍流改变。那么二次分离点将向外移,并使主涡变强。而对钝前缘三角翼来说,雷诺数主要影响前缘分离涡的起始位置,雷诺数越大,前缘分离涡的起始位置越靠后(如图 11[18])。
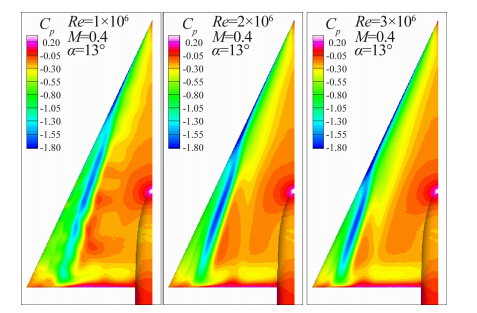 |
| 图 11 雷诺数对前缘涡的影响示例Fig. 11 Example of effects of Reynolds number on leading edge vortex |
如图 12,Ma=0.2、α=8°时在机翼前缘出现了前 后两个分离区。随着雷诺数的增大,分离区明显变 小,分离涡的起始点明显向翼梢方向移动。图 13是Ma=1.5、α=12°时雷诺数对流场的影响。由于激波边界层干扰,引起波后流场分离;随着雷诺数的增大,激波向后移动,分离的范围减小,同时在机身后部的分离区明显变小。
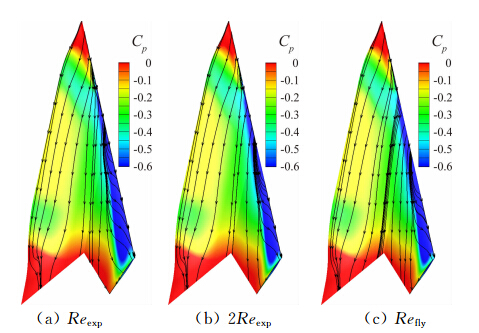 |
| 图 12 雷诺数对流场的影响(Ma=0.2,α=8°)Fig. 12 Effects of Reynolds number on flow fields(Ma=0.2,α=8°) |
 |
| 图 13 雷诺数对流场的影响(Ma=1.5,α=12°)Fig. 13 Effects of Reynolds number on flow fields (Ma=1.5,α=12°) |
根据前面的分析,计算的三个雷诺数对气动特性的影响较小。由以往的经验,飞行器气动特性随雷诺数变化都存在一个自准区,达到自准区雷诺数 后,气动特性随雷诺数变化很小[9]。因此怀疑本文计算的雷诺数接近或者达到了自准区雷诺数,为此,我们增加了如表 9所示的计算状态,来检验此推论。
图 14~图 16是Ma=0.8、α=4°、16°和32°时的雷诺数对气动特性的影响曲线。由图可见,在雷诺数 较小时,雷诺数变化对气动力的影响明显大于雷诺数大 的情况。α=4°时,雷诺数由0.1Reexp变化到Reexp,升 力系数增加了1.44%,阻力系数减小了14.5%,低头俯仰力矩系数增加了2.60%,升阻比增加了18.7%。而雷诺数由Reexp变为Refly时,升力系数增加了0.835%,阻力系数减少了9.12%,低头俯仰力矩系数增加了1.22%,升阻比增加了10.6%。其他两个 攻角的计算结果与α=4°规律相同。可见随着雷诺数的增大,雷诺数对气动特性的影响明显减小,本文计算的三个雷诺数已经接近自准区雷诺数,因此对气动特性的影响较小。
| Re/Reexp | Ma | α/(°) | |
case1 case2 case3 case4 | 0.1 0.2 0.5 5 | 0.8 | 4,16,32 |
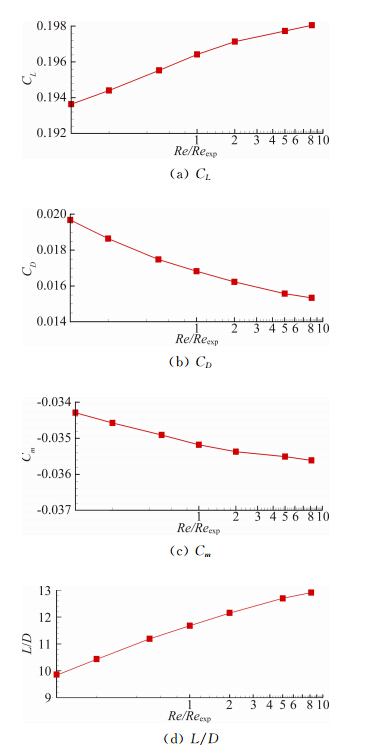 |
| 图 14 雷诺数对气动特性的影响(Ma=0.8,α=4°)Fig. 14 Effects of Reynolds number on aerodynamic coefficient(Ma=0.8,α=4°) |
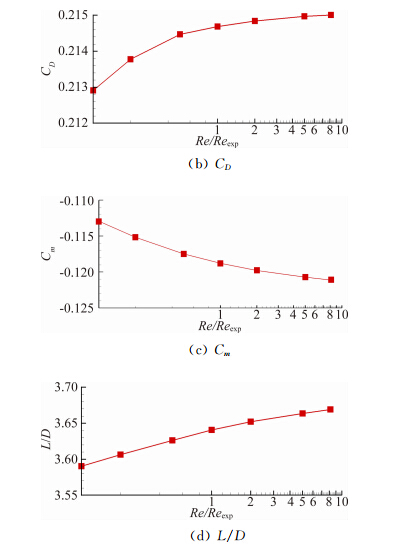 |
| 图 15 雷诺数对气动特性的影响(Ma=0.8,α=16°)Fig. 15 Effects of Reynolds number on aerodynamic coefficient(Ma=0.8,α=16°) |
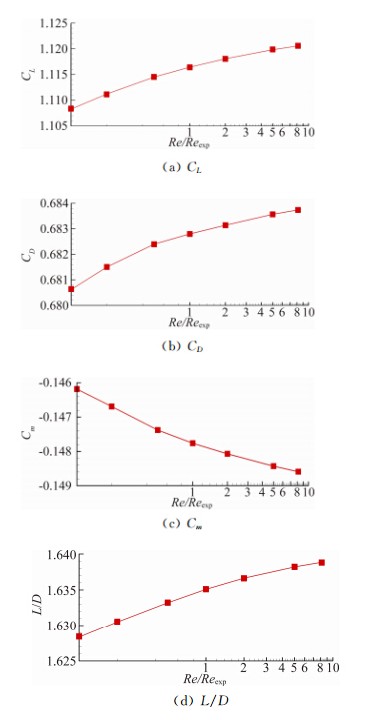 |
| 图 16 雷诺数对气动特性的影响(Ma=0.8,α=32°)Fig. 16 Effects of Reynolds number on aerodynamic coefficient(Ma=0.8,α=32°) |
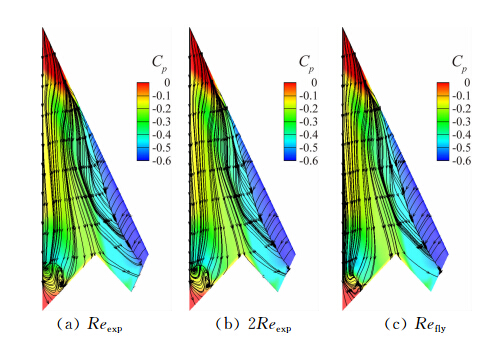
图 17是Ma=0.8、α=16°的雷诺数对压力分布及物面附近流线的影响图。当雷诺数由0.1Reexp增大到Reexp,主涡的再附线、二次分离的分离线和再附线明显向外侧移动,而雷诺数由Reexp增大到Refly时,移动的幅度非常小。
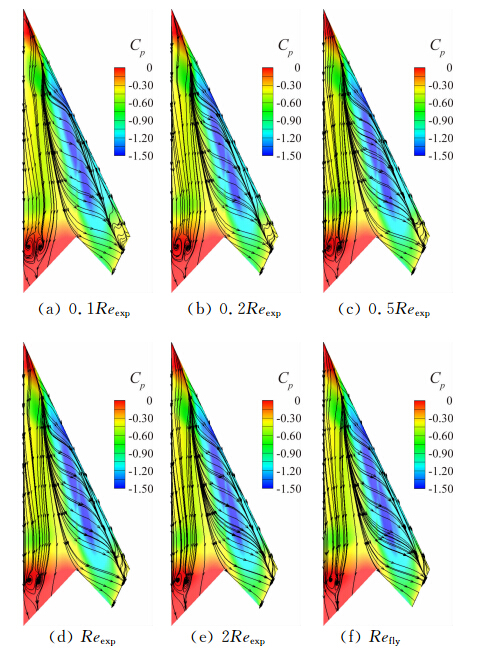 |
| 图 17 雷诺数对流场的影响(Ma=0.8,α=16°)Fig. 17 Effects of Reynolds number on flowfield (Ma=0.8,α=16°) |
本文采用数值模拟方法研究了雷诺数对小展弦比飞翼标模流场气动特性的影响问题。关于小展弦比飞翼标模的雷诺数影响,得到如下结论:
(1) 在本文计算的三个雷诺数:试验雷诺数、二倍试验雷诺数和飞行雷诺数条件下,雷诺数对升力系数、阻力系数和俯仰力矩系数曲线影响较小,对最大升阻比有一定的影响。
(2) 与一般小展弦比机翼外形相同,小攻角情况下,雷诺数主要影响摩阻的大小、边界层厚度和激波边界层干扰。随着雷诺数增大,摩擦阻力减小,而对压阻影响很小。大攻角时,雷诺数增大,除引起摩阻减小外,压阻也有明显增大。
(3) 与一般钝前缘三角翼相同,在亚声速时,雷诺数主要影响分离涡的起始位置和强度;跨声速和超声速时,雷诺数还会影响到激波的位置和强度。
(4) 试验雷诺数接近于小展弦比飞翼标模的自准区雷诺数,因此试验雷诺数下的气动特性与飞行雷诺数的情况非常接近,在风洞试验结果外推时只需对阻力系数和最大升阻比进行修正。
(5) 由于未考虑转捩的影响,因此本文的计算与实际试验条件(贴转捩带)有一定的差异,在未来的研究中需要进一步考虑固定转捩的影响。
| [1] | Johnson F T, Tinoco T, Jong Yu N. Thirty years of development and applicationof CFD at Boeing commerical airplane seattle[R]. AIAA 2003-3439. |
| [2] | Vaucheret X. Flight/ground testing facilities correlation[R]. ADA 026937, AGARD CP-187, 1976. |
| [3] | The Fluid Dynamics Panel Working Group 04. Experimental data base for computer program assessment[R]. AGARD AR-138, 1979. |
| [4] | Agnew J W, Mello J F. Correlation of F-15 flight and wind tunnl test control effectiveness[R]. AGARD CP-262, 1979. |
| [5] | Agnew J W, Mello J F. Ground/flight test techniques and correlation[R]. AGARD CP-339, 1983. |
| [6] | AGARD Fluid Dynamics Panel Working Group 15. Quality assessment for wind tunnel testing[R]. AGARD AR-304,1994. |
| [7] | Haines A B, Young A D. Scale effects on aircraft and weapon aerodynamics[R]. AGARD AG-323, 1994. |
| [8] | Dennis M Bushnell. Scaling: wind tunnel to flight[R]//Annu. rev. fluid mech., 2006. |
| [9] | Zhang P H, Zhou N C, Deng Y Q, et al. The effects of Reynolds number on airplane aerodynamic characteristics[J]. Acta Aerodynamica Sinica, 2012, 30(6):693-698.(in Chinese) 张培红, 周乃春, 邓有奇, 等. 雷诺数对飞机气动特性的影响研究[J]. 空气动力学学报, 2012, 30(6): 693-698. |
| [10] | Zhang Y B, Zhou N C, Wu X J, et al.Comparison of turbulence models for the computation of ONERA-M6 wing[C]//The conference of turbulence transition on practice, 2010. 张耀冰, 周乃春, 吴晓军, 等. 两种湍流模型在计算ONERA-M6机翼绕流流场中的比较[C]//工程湍流转捩学术会议, 2010. |
| [11] | Ma M S, Zhang Y B, Deng Y Q, et al. Investigation of Reynolds number effects on transport aircraft's wing, fuselage and wing-body by numerical simulation[J]. Acta Aerodynamica Sinica, 2011, 29(2):194-198. (in Chinese) 马明生, 张耀冰, 邓有奇, 等. 运输机机翼、机身和翼身组合体气动特性雷诺数效应的数值模拟研究[J]. 空气动力学学报, 2011, 29(2): 194-198. |
| [12] | Spalart S R. A one-equation turbulence model for aerodynamic flows[R]. AIAA 92-0439, 1992. |
| [13] | Menter F R, Rumsey L C. Assessment of two-equation turbulence models for transonic flows[R]. AIAA 94-2343. |
| [14] | Deng Y Q. Numerical simulation of Navier-Stokes equations for flowfields around the vehicles of complex configuration[D]. Beijing: Institute of aviation science and engineering, Beihang University. 2006 邓有奇. 飞行器复杂外形流场NS方程数值模拟研究[D]. 北京:北京航空航天大学航空科学与工程学院, 2006. |
| [15] | Zhang Y B, Zhou N C, Chen J T, et al. Numerical investigation of the support bracket influence of small aspect ratio fly-wing model[C]//The Aerodynamics Research Corpus, 2013, 23: 235-240. 张耀冰, 周乃春, 陈江涛, 等. 小展弦比飞翼标模支撑干扰数值模拟研究[C]//空气动力学研究文集, 2013, 23: 235-240. |
| [16] | Sherrie L Krist, Robert T Biedron, Christopher L Rumsey. CFL3D user's manual (version5.0)[R]. NASA TM 208444, 1998. |
| [17] | John C Vassberg. A unified baseline grid about the common research model wing-body for the fifth AIAA CFD drag prediction workshop[R]. AIAA 2011-3508, 2011. |
| [18] | Andreas Schutte, Heinrich Ludeke. Numerical investigations of the VFE-2 65° rounded leading edge delta wing using the unstructured DLR-TAU-Code[R]. AIAA 2008-398, 2008. |


