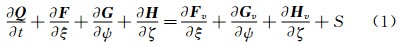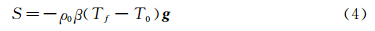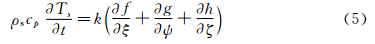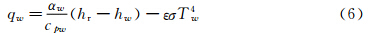2. 南京航空航天大学 航空宇航学院, 江苏 南京 210016
2. College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
0 引 言
当飞行器较长时间以马赫数3以上的速度飞行,由于受到气动加热的影响,飞行器蒙皮的温度将急剧上升,热量通过机体结构向舱室内部传递,使舱内环境条件发生变化,如若不加以防护和控制,将对舱内的各种设备的正常工作产生不利影响。因此,气动热 [CM(22*2]问题,以及在此基础上的防隔热设计需要在设计阶段 段进行重点关注。其中,准确预测气动加热、结构温度分布及舱内温度分布,是确定飞机舱内热环境及进行防隔热设计的一个重要前提。
从物理原理出发,气动热问题的实质是由高速可压缩流动热力学、粘性附面层能量转换、热辐射、热对流以及热传导等多种条件共同决定的。若忽略各个学科之间的耦合效应,仅采用气动热-结构传热独立求解的方法,则分析结果势必会存在一定误差。因此,有必要探索一种能够在工程设计中应用的气动加热-固体传热-舱内热环境的耦合分析方法。
为了准确模拟飞行器表面的气动热及结构传热,进而开展防隔热设计,国内外学者开展了大量的流动-热-结构耦合计算的研究。1987年Wieting等[1,2]采用气动加热/结构耦合方法模拟了激波相互作用下的圆柱壳前缘,并进行了高温风洞试验,成为耦合计算的标准算例。1989年,Dechaumphai等[3]采用有限元法对二维圆柱进行了气动热/结构传热耦合计算。2011年,Culler等[4]通过耦合工程方法和Nastran对高超声速飞行器进行了气动-热-结构变形的分析,并对定常分析、准定常分析及非定常分析进行了对比研究。2011年,Blades等[5]通过耦合气动热求解器和结构有限元求解器对高超声速飞行器外形进行了分析,其中结构求解器采用了ABAQUS,而气动热求解器分别采用了CHEM CFD和工程软件MINIVER两种方式进行对比研究。2000年,黄唐等[6]人采用松耦合方法对二维圆柱进行了模拟,其中流场采用了有限差分方法,结构传热采用了有限元方法。2002年,耿湘人等[7]采用了一种将气体流动和固体传热作为统一物理现象的一体化计算方法,并对二维圆柱进行了模拟。2003年,夏刚等[8]采用有限体积法结合有限元法的方式进行二维气动热/结构传热耦合计算,并研究了松耦合及紧耦合方法对结果的影响。2010年,李鹏飞[9]采用紧耦合的方法研究了类航天飞机的机头结构与高速流场的耦合传热问题,其中流体区域和固体区域都采用了有限差分方法。2011年张兵[10]开发了基于现有商业软件FASTRAN和ANSYS的用于多物理场耦合计算的接口平台。2012年,耿丹萍[11]基于气动热-气动弹性双向耦合的思路,建立了气动力、气动热、热传导和气动弹性的耦合计算平台。2013年,黄杰[12]采用松耦合的计算方法,利用MPCCI耦合Fluent和Abaqus进行了气动热-结构传热耦合分析。2014年,陈鑫等[13]基于工程估算方法对进行了翼面气动加热、辐射换热与瞬态热传导的耦合分析。上述研究主要集中在耦合气动热及结构传热进行求解,未进一步考虑舱内流场相关问题,以及舱内温度场的变化和影响,不能得到舱内准确的温度分布以指导防隔热和环控系统设计。
本文采用了两套计算模型,两种求解器及一个数据交换文件的计算结构,构建了一种针对流场-热-结构的多物理场耦合分析方法。将舱外区域作为一套模型,而舱壁结构区域及舱内区域作为一套模型。两套模型分别采用一种有限体积法求解器进行瞬态求解,并通过一个数据交换文件传递舱外壁面处的瞬态热流及温度实现紧耦合计算。气动热求解采用单独的求解器可以方便的进行紧耦合及松耦合比较研究,也可以针对具体工程问题选择合适工程估算方法同结构传热及舱内流场进行耦合求解。通过本文的分析方法,不仅实现了舱外气动热-舱壁结构传热的耦合求解,同时瞬态分析了舱内流场及温度场的动态演化特性,验证了相关隔热设计的正确性。通过本文的方法,可为高速飞行器防隔热设计提供重要仿真手段,并为舱内环控系统设计提供设计输入条件。 1 计算方法
本文所提出的基于多物理场耦合理论的计算方法在舱外流体区域、舱体结构及舱内流体区域,分别采用两套计算模型、两套计算方法,并通过一个数据交换文件,完成在一次仿真计算当中完整的模拟舱外气动加热、舱壁热传导、机舱内部对流、辐射及传导现象。整个计算模型如图 1所示意。
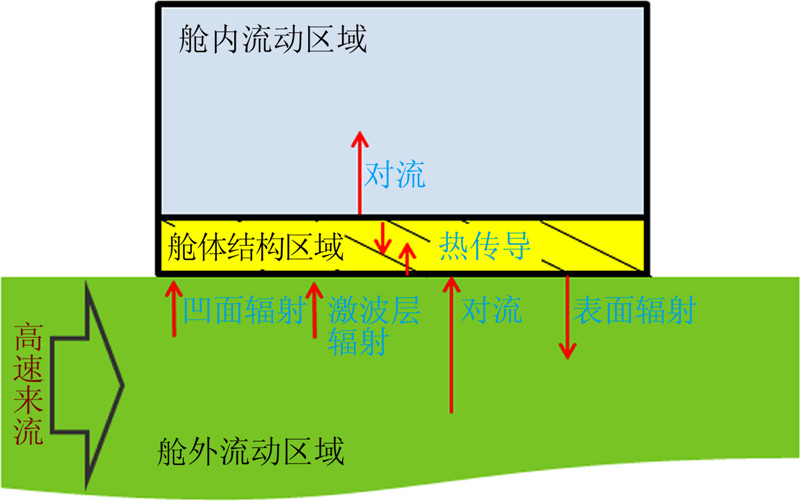 |
| 图 1 计算模型简图Fig. 1 Sketch of simulation model |
舱外流场指飞行器所处的外流场,由相应的边界条件构成,如图 1所示。舱外流场部分的控制方程采用基于理想气体假设的无化学反应非定常层流可压缩Navier-Stokes方程,在计算坐标系下的微分形式如下:
式中,Q为守恒变量,F、G、H为无粘通量,F v、 G v、 H v为粘性通量,ξ、ψ、ζ为计算坐标系下三个方向的坐标,S为源项。气体满足理想气体状态方程:
其中:ρ为密度,p为压力,T为温度,R为摩尔气体常数。使用有限体积法对流体控制方程进行离散求解,其中无粘通量采用中心差分格式,粘性通量采用Roe’s FDS离散格式[14],并使用二阶Min-Mod限制器[15]。为了避免FDS类格式可能出现的非物理解,在此引入了Harten-Yee型熵修正方法[16]。时间离散格式采用双时间步法的隐式时间离散方法[17]。因为对于高速流动问题,即使是隐式格式,时间步长的选取也将受到很大的限制,需要维持在一个很小的值,这样的求解效率对于工程实际应用来讲是不能接受的;而对于双时间步法,每一步迭代都是以伪时间步长推进,真实的物理时间步长从理论上讲可以任意选取,而不会对稳定性产生影响,从而大大提高了计算效率。考虑到为了提高热流计算精度,外部流场的计算网格数量可能会比较大,因此在计算外流场时采用并行计算,可以在保证精度的基础上大大节省计算时间。 1.2 机舱结构传热及舱内流动传热计算
舱壁结构区是指舱段周围的结构框、壁、地板形成封闭的舱室,舱内流场区是指舱段内部的空间,如图 1所示。由于舱内流场主要为低速不可压流体,密度为常数,如式(3)所示:
对于不可压流体,适合采用分离式解法。因此本文采用基于同位网格的PISO算法进行求解方程(1)。同时通过Boussinesq假设考虑舱内温度变化对动量方程中源项的影响。源项的方程形式如下:
式中,ρ0为参考密度,g 为重力加速度,β为热膨胀系数,Tf为舱内流体温度,T0为参考温度。取舱内初始温度及密度为参考温度及参考密度。舱壁结构传热求解基于各向同性假设的非稳态热传导方程,计算坐标系下的方程形式如下:
式中,ρs为结构密度,cp为比热,k为导热系数,Ts为温度,f、g、h分别为温度在坐标系三个方向的空间导数。其中k为温度的函数。舱壁结构区域空间上采用中心差分格式的有限体积法进行求解,时间上采用欧拉法推进[17]。由于舱体结构传热的时间尺度远大于舱外气动热的时间尺度,同舱内自然对流的时间尺度接近。因此舱体结构传热同舱内对流辐射作为同一计算模型,采用同一时间步长,在每步求解时进行内迭代,直到舱体结构温度场与舱内流场温度场均满足收敛条件。 1.3 机舱外壁边界条件
舱外高速气流与机舱外壁之间主要通过对流换热、凹面辐射传热和激波层辐射换热将气动热传递给舱壁,通过表面辐射将热量传递到外部空间,并通过结构传热将能量传递到结构内部。在不考虑凹面辐射计激波层辐射的情况下,壁面热平衡公式为:
式中,qw为壁面上单位面积热流量;αw为壁面对流换热系数;cpw为壁面气体比热;hr为气体的恢复比焓;hw为壁面气体比焓;ε为辐射率;σ为斯忒藩·玻耳兹曼常量;Tw为壁面气体温度。在定常状态下qw=0,此时的Tw即为平衡温度。 1.4 耦合求解方法整个耦合求解结构由两个模型、两个求解器和一个数据交换文件组成,如图 2所示。内/外流与热/固耦合求解时,外部流场会读取文件中由结构传热求解的壁面温度作为边界条件,求解后将求得的壁面热流保存在外部文件中。在进行舱内计算时,通过文件读取外部流场计算生成的壁面热流,在正确的读入热流并且计算完毕之后会将结果中的壁面温度反馈给外 部流场开展下一步的热流计算,从而实现两者之间的 实时耦合。其中,内外两套网格按节点一一对应关系构建,保证两个求解器在调用壁面边界上每个节点信息时完全对应,这样既提高了数据交换的效率,又避免了数据插值引起的精度降低问题。需要指出的是,由于外流场为高速可压流体,时间尺度较小,而内流场为低速不可压流体,时间尺度较大,因此内、外两部分的计算采用了不同的求解器和不同的时间步长来提高各区域求解的精度及收敛效率。同时,为了保证整个仿真计算的时间精度,本文通过控制数据交换文件的时刻,确保内、外两部分计算的物理时间是保持一致的。
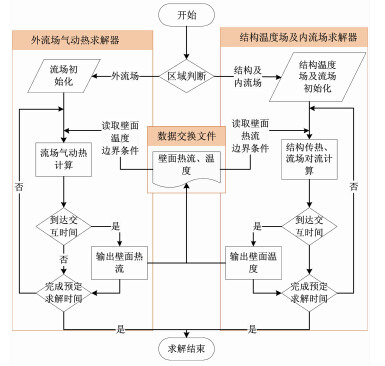 |
| 图 2 计算流程示意图Fig. 2 Sketch of simulation process |
本文通过选择飞行器机身中部机腹附近的一个舱段,将相关的仿真过程作为算例来验证本文的计算方法。设定飞行器来流马赫数为3.5,并按图 3确定舱室的几何模型以及内部温度边界条件,图 4显示的是机舱的结构模型由三部分组成,分别为:结构层(舱门结构),中间层(胶层)与隔热层(隔热材料)。机舱的三层密度、比热、热导率数据如表 1所示。
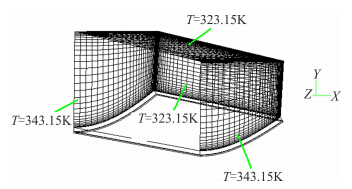 |
| 图 3 舱段半模模型以及温度边界条件Fig. 3 Half model of the simulation and temperature boundary conditions |
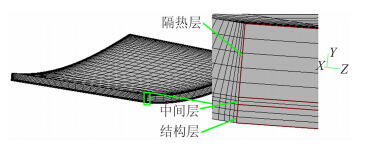 |
| 图 4 舱门结构Fig. 4 Structure of the bay door |
| 类型 | 密度 /(kg·m-3) | 比热 /(J·kg-1·K-1) | 热导率 /(W·m-1·K-1) |
| 隔热层 | 200 | 1000 | 0.33 |
| 中间层 | 300 | 800 | 0.6 |
| 结构层 | 4500 | 700 | 10 |
计算中发现气动热的时间尺度较小可以迅速稳定,随后受到结构温度变化而有所波动,如图 5所示为机舱外表面平均热流的变化过程。
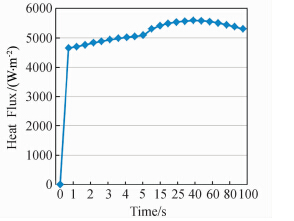 |
| 图 5 机舱外表面平均热流变化Fig. 5 History of mean heat flux at the out surface of bay door |
气动加热可以迅速穿透结构层,传导到中间层,使结构中间层的温度也达到与外流场壁面相同的温度,如图 6所示为第5s时的温度分布状态。
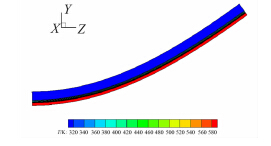 |
| 图 6 舱门横截面温度分布Fig. 6 Temperature distribution at the middle cut of bay door |
而隔热层由于热导率较低,能大大延缓了热量的传导。从图 7可以看出30s以前隔热层温度几乎没有变化,到30s后才对舱体内壁有了微弱的加热效果,证明隔热材料能够发挥十分良好的隔热作用。
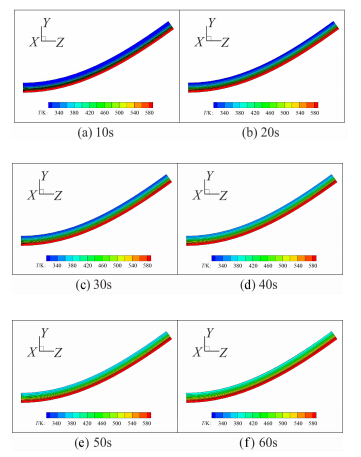 |
| 图 7 舱门横截面温度分布Fig. 7 Temperature distribution at the middle cut of bay door |
随着时间的推移外流场对舱体的气动加热穿透了隔热层,开始对舱内流场进行加热。图 8给出了30s后舱内温度的变化过程。舱内的主要传热方式为热对流。图 9给出了第60s的速度矢量图,看以明显看出由于上下壁面温差引起的涡流分布。图 10给出了第60s的速度分布,可以看出此时最大速度为0.31m/s。
 |
| 图 8 舱内横截面温度分布Fig. 8 Temperature distribution at the middle cut of bay |
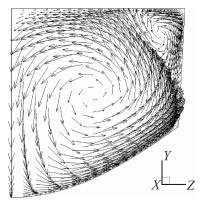 |
| 图 9 舱内横截面速度矢量分布Fig. 9 Flow vector at the middle cut in the bay |
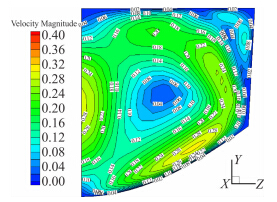 |
| 图 10 舱内横截面速度分布Fig. 10 Velocity distribution at the middle cut in the bay |
如图 11(a)所示,选取舱段对称面中间截面上的五个特征点,观察温度变化情况。由图 11(b)可以看出,在计算的30s时间内,结构层和中间层的A、B、C点温度迅速趋于收敛平衡,而隔热层内侧D点及舱内E点的温度变化不大。30s后,气动加热对结构层和中间层温度影响不大,而此时隔热层内侧D点及舱内E点受气动热影响,温度平稳升高。
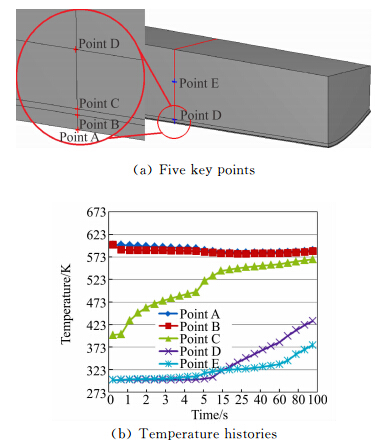 |
| 图 11 五个关键位置的温度变化Fig. 11 Temperature histories of five key points |
通过对联合CFD求解器与多物理场求解器的研究,本文得出了一种耦合计算方法,并应用这种方法对高马赫数飞行器内部舱温问题进行了计算分析,全文得到的重要结论如下:
(1) 采用两套模型、两种求解器、一个数据交换文件的计算构架,可以完成流/热/辐射多场耦合的固体隔绝内外流温度动态变化的仿真分析;
(2) 通过壁面条件交换文件的形式解决了舱外气动热求解器和舱体结构及舱内流场求解器之间的数据交换问题;
(3)通过本文建立的方法,可对较为复杂的防隔热设计进行仿真计算,得到的舱温分布则可进一步指导环控系统的设计工作。
本文论述的计算方法由于实时耦合了结构、内部流场、辐射等热问题相关量,因此在计算量上远远高于一般的气动热CFD计算,但是其在物理上的完整性和精确性是传统气动热计算所难以企及的。考虑到工程应用,还需要在外部流场的迭代步长、计算精度、收敛性之间做进一步研究,以提高整个计算的效率。
| [1] | Wieting A R, Holden M S. Experimental study of shock wave interference heating on a cylindrical leading edge at Mach 6 and 8[R]. AIAA-87-1511, 1987. doi:10.2514/6.1987-1511 |
| [2] | Wieting A R. Experimental study of chock wave interference heating on a cylindrical leading edge[R]. United States:NASA Langley Research Center, Hampton, VA, 1987. |
| [3] | Dechaumphai P, Thornton E A, Wieting A R. Flow-thermal-structural study of aerodynamically heated leading edges[J]. Journal of Spacecraft, 1989, 26(4):201-209. |
| [4] | Culler A J, McNamara J J. Fluid-thermal-structural modeling and analysis of hypersonic structures under combined loading[R]. AIAA 2011-1965. |
| [5] | Blades E L, Miskovish R S, Nucci M, et al. Towards a coupled multiphysics analysis capability for hypersonic vehicle structures[R]. AIAA 2011-1962. |
| [6] | Huang Tang, Mao Guoliang, Jiang Guiqing, et al. Two dimensional coupled flow-thermal-structural numerical simulation[J]. Acta Aerodynamica Sinica, 2000, 18(1):115-119. (in Chinese)黄唐, 毛国良, 姜贵庆, 等. 二维流场、热、结构一体化数值模拟[J]. 空气动力学学报, 2000, 18(1):115-119. |
| [7] | Geng Xiangren, Zhang Hanxin, Shen Qing, et al. Study on an integrated algorithm for the flowfields of high speed vehicles and the heat transfer in solid structures[J]. Acta Aerodynamica Sinica, 2002, 20(4):422-427. (in Chinese)耿湘人, 张涵信, 沈清, 等. 高速飞行器流场和固体结构温度场一体化计算新方法的初步研究[J]. 空气动力学学报, 2002, 20(4):422-427. |
| [8] | Xia Gang, Liu Xinjian, Cheng Wenke, et al. Numerical simulation of coupled aeroheating and solid heat penetration for a hypersonic blunt body[J]. Journal of National University of Defense Technology, 2003, 25(1):35-39. (in Chinese)夏刚, 刘新建, 程文科, 等. 钝体高超声速气动加热与结构热传递的耦合数值计算[J]. 国防科技大学学报, 2003, 25(1):35-39. |
| [9] | Li Pengfei, Wu Songping. Coupling calculation of heat conduction in 2D column in hypersonic flows[J]. Missiles and Space Vehicles, 2010, 6:34-37. (in Chinese)李鹏飞, 吴颂平. 二维圆柱在高超声速气流中的耦合传热计算[J]. 导弹与航体运载技术, 2010, 6:34-37. |
| [10] | Zhang Bing, Han Jinglong. Multi-field coupled computing platform and thermal transfer of hypersonic thermal protection structures[J]. Acta Aeronoutica et Astronautica Sinica, 2011, 32(3):400-409. (in Chinese)张兵, 韩景龙. 多场耦合计算平台与高超声速热防护结构传热问题研究[J]. 航空学报, 2011, 32(3):400-409. |
| [11] | Geng Danping. Based aerothermoelastic analysis of an insulated panel in hypersonic flow[J]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2012. (in Chinese)耿丹萍. 基于双向耦合的高超声速壁板热气动弹性问题研究[D] [硕士学位论文]. 南京:南京航空航天大学, 2012. |
| [12] | Huang Jie. Study on hypersonic vehicle fluid-thermal-structure multi-physics coupling calculation[J]. Harbin:Harbin Institute of Technology, 2013. (in Chinese)黄杰. 高超声速飞行器流热固多物理场耦合计算研究[D].[硕士学位论文]. 哈尔滨:哈尔滨工业大学, 2013. |
| [13] | Chen Xin, Liu Li, Li Yulin, et al. Coupled study of aerodynamic heating, radiative heat transfer and heat conduction for airfoils of hypersonic vehicles[J]. Journal of Ballistics, 2014, 26(2):1-5. (in Chinese)陈鑫, 刘莉, 李昱霖, 等. 高超声速飞行器翼面气动加热、辐射换热与瞬态热传导的耦合分析[J]. 弹道学报, 2014, 26(2):1-5. |
| [14] | Vinokur M. An analysis of finite-difference and finite-volume formulations of conservation laws[J]. Journal of Computational Physics, 1989, 81:1-52. |
| [15] | Rider W J. Methods for extending high-resolution schemes to non-linear systems of hyperbolic conservation laws[J]. International Journal for Numerical Methods in Fluids, 1993, 17:861-885. |
| [16] | Kermani M J, Plett E G. Modified entropy correction formula for the roe scheme[R]. AIAA 2001-0083. |
| [17] | Jameson A. Time dependent calculations using multigrid with application to unsteady flows past airfoils and wings[R]. AIAA-91-1956, 1991. |