自20世纪60年代通过环量控制(Circulation Control)方法提高翼型升力的概念被提出以来,已经有大量的学者对其进行了研究。环量控制翼型利用高压空气由翼型内部向外喷射一薄层空气,射流在科安达效应(Coanda Effect)的作用下沿着翼型表面向后缘流动,增大沿翼型表面的环量,进而提高翼型的升力。
量控制技术在工程上已经应用到了直升机无尾桨反扭矩系统(NOTARTM System)内,使传统的用以支撑常规尾桨的尾梁转变为在旋翼下洗流中工作的气动部件,提供了部分用以平衡直升机主旋翼反扭矩的气动力,图 1为直升机无尾桨反扭矩系统的组成和环量控制尾梁的工作原理。无尾桨反扭矩系统在安全性[1, 2, 3]、可靠性[4]、操纵性[5, 6, 7]、振动和噪音水平[4, 5, 6]等诸多方面都有突出的优点,然而略大的功率需求导致了该技术没有得到广泛应用。其中环量控制尾梁具备优化的潜力,可能使无尾桨反扭矩系统所需功耗相当甚至更少。
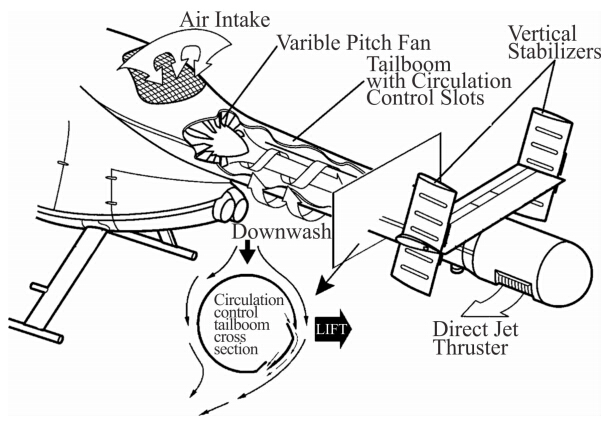 |
| 图 1 无尾桨反扭矩系统的组成及环量控制尾梁工作原理Fig. 1 Components of the NOTARTM system and working principle of circulation control tail boom |
很多中外学者已经通过试验或模拟计算方法对环量控制尾梁技术进行了研究[4, 5, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18],然而公开发表的对环量控制尾梁的截面形状研究却非常少,只有David T Fisher于1994年通过试验方法测量了圆形截面和50%椭圆形截面的环量控制尾梁的升力和阻力[4],但是由于测试条件和模型尺寸上的差异无法通过对比得出关于截面形状与升力之间关系的任何结论。目前实际采用的环量控制尾梁都采用圆截面。非圆截面的曲率可以设计,从而引导附壁气流,使其在恰当的位置脱离壁面,从而增强喷射气流的效果。 1 数值计算方法 1.1 测试模型参数及试验参数
参考文献[4]中试验测试的环量控制尾梁模型是一个外径114.3mm、壁厚6.4mm的空心圆柱。沿空心圆柱轴线方向开有一条长508mm、宽1.0 mm、喷射角约为51°的狭缝。测试参数如表 1所示,表中Cμ、vjet和v∞分别表示动量因数(Momentum Coefficient[4])、狭缝出口处气流速度和旋翼下洗流速度。其中动量因数定义为:
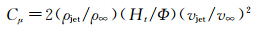
| Cμ | vjet/(m·s-1) | v∞/(m·s-1) |
| 0.3 | 72.1 | 18.0 |
| 0.4 | 77.5 | 16.7 |
| 0.5 | 82.5 | 16.0 |
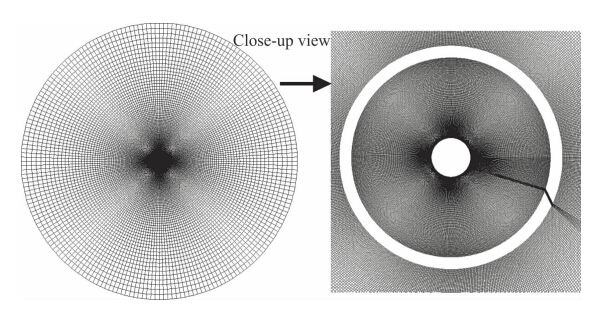
如图 2所示,计算区域为一个二维的环形,环形的内边界位于尾梁的内壁面内,外边则位于外壁面之外。在尾梁的内部建立计算网格而不是仅仅在狭缝出口处设置速度出口边界条件是为了避免边界条件对狭缝出口处喷射气流造成人为影响。
计算区域通过几个同心圆划分成几个区域(如图 2所示)。为了尽量提高计算精度并减少计算时间,近壁面网格更密集。域A、B、D和E划分成四边形网格,而域C划分成三角形网格。计算网格如图 3所示。
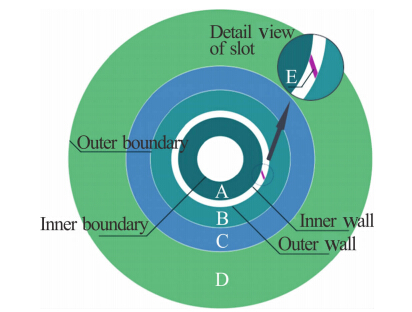 |
| 图 2 计算域的划分示意图Fig. 2 Division of calculation field |
升力计算结果对尾梁外部近壁面第一层网格与壁面之间的距离比较敏感,本文中该距离设置为 0.3mm。为了避免边界条件对计算结果的影响,将尾梁内部和外部的计算边界的直径分别设置为20mm和10m,分别约为尾梁外壁面直径的1/5和100倍。 1.3 控制方程、湍流模型及边界条件
采用二维定常、有粘性、不可压缩的Navier-Strokes控制方程。近壁面处理方法采用标准壁面方程。湍流模型采用可实现的k-Epsilon模型。压力通过体积力法插值,而动量、湍动能和湍流耗散率采用三阶逆风格式插值。对所有壁面施加无滑移边界条件。计算域的内边界施加速度入场边界条件,并通过调整其数值大小调整狭缝射流速度。计算域的外边界施加速度入场边界条件,用来模拟旋翼的下洗流。 1.4 方法验证
图 4所示为计算结果与测试结果之间的对比。对比显示:在发生气流分离之前,模拟计算结果随动量因数和狭缝迎角的变化趋势与测试结果相同,在狭缝迎角从100°到118°之间升力在数值上与实验吻合得很好。模拟计算还预测到了气流发生分离时的狭缝迎角。
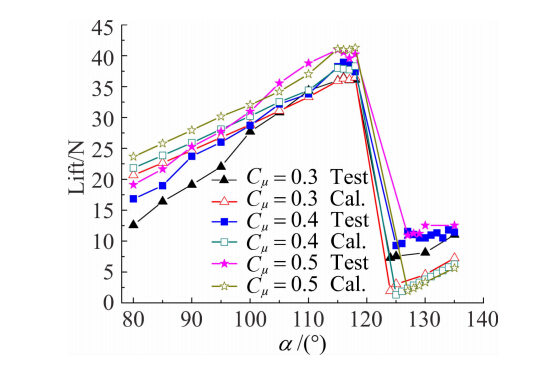 |
| 图 4 升力的计算值与试验值之间的对比Fig. 4 Comparison of lift calculated and test data |
在实际工程应用中,环量控制尾梁以一固定的经过优化的狭缝迎角安装到直升机机身上,考虑到直升机不同的飞行状态和突风的影响,环量控制尾梁应该在一定范围内(本文中取连续10°)都可以产生较大的升力。比如该试验模型环量控制尾梁安装到机身的优化狭缝迎角约为113°。模拟计算结果显示该计算方法能够找出最优狭缝迎角,区分各参数对尾梁升力的影响并准确预测发生气流分离的狭缝迎角,因而可以用于环量控制尾梁的截面形状分析研究。 2 截面形状和参数说明
图 5为本文模拟计算的环量控制尾梁截面形状及狭缝相关参数的示意图。本文中研究的截面形状可以看作为由左右两个半椭圆结合而成的一个形状,其中左半椭圆的垂直轴与右半椭圆的垂直轴重合且长度与基准圆外径相同。右半椭圆的半水平轴长度b分别等于a、Φ/2和Φ-a时,图中的截面形状就分别形成椭圆、左边半椭圆右边半圆和左边半个高椭圆右边半个扁椭圆三种不同形式,分别记作S1、S2和S3,并用2a/Φ的百分比来描述这三种不同截面形状与基准圆截面之间的相似程度,本文中称这个百分数为“似圆度”,任一似圆度为100%的截面都是直径为Φ的圆。其它截面形状及狭缝相关的参数列于表 2。
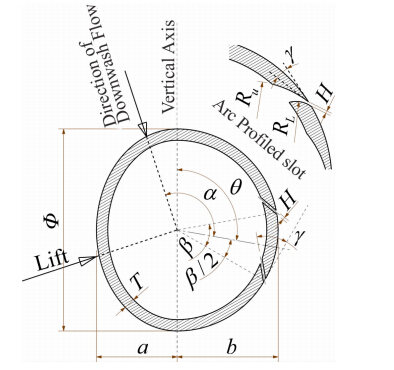 |
| 图 5 截面形状及狭缝几何参数示意图Fig. 5 Schematic diagram of the cross section shape and geometry parameters of the slots |
| 符号 | 名称 | 解释说明 |
| T | 壁厚 | T=6.4mm |
| Φ | 基准直径 | 如无说明Φ=114.3mm |
| H | 缝宽 | 狭缝最窄处宽度,如无说明H=1mm |
| Ht | 总缝宽 | 多条狭缝的总宽度/mm |
| α | 狭缝迎角 | 下洗流方向与狭缝平均位置之间的夹角/(°) |
| β | 缝间角 | 两条狭缝之间的夹角,如无说明β=0°,即只有一条狭缝 |
| γ | 喷射角 | 狭缝出口处气流方向与当地尾梁轮廓线切线之间的夹角,如无说明γ=40° |
| θ | 缝位角 | 狭缝平均位置与椭圆垂直轴之间的夹角,如无说明θ=110° |
| RU | 上壁半径 | 弧形狭缝的上壁面半径,RU=45mm |
| RL | 下壁半径 | 弧形狭缝的下壁面半径,RL=15mm |
图 6~图 12所示为不同截面环量控制尾梁在不同条件下升力随狭缝迎角的变化曲线。其中图 6模型 采用平直狭缝、几何参数为表 2中的默认值,vjet与v∞分别为77.5m/s和16.7m/s。将M1模型的几何和试验参数设为基准以便于比较,除有说明,以下所有计算模型的几何参数及试验参数均与M1一致。从图 6中可以看出:(1)对S1和S2截面,整体上非圆截面产生的升力小于相同狭缝迎角下圆形截面产生的升力,且非圆截面产生的升力分别随着似圆度的提高而提高;(2)S1截面形状之间的性能差距比较明显,S2截面之间的性能差距相对较小。S3截面形状之间在狭缝迎角较小时性能差别较小,在狭缝迎角较大时似圆度越低越容易出现气流分离现象;(3)本组计算中最优截面形状为90%相似度S3截面(简写为90%S3),但是90%S2和圆截面的性能都非常接近最优截面。
 |
| 图 6 平直单狭缝,参数见表 2,vjet=77.5m/s,v∞=16.7m/s(基准模型,M1)Fig. 6 Single strait slot,parameters listed in table 2,vjet=77.5m/s,v∞=16.7m/s (referenced model,M1) |
图 7显示的模型(M2)喷射角为30°。从图中可 以看出:(1)各截面形状产生的升力曲线分别与基准组相似,但是存在非圆截面的最大升力明显大于圆截面最大升力;(2) S2截面间升力差距相对较小,低似圆度S3截面容易出现气流分离。通过与基准组模型对比可以发现,喷射角较小时各截面形状产生的升力普遍增大,且增强了气流的附壁稳定性(与文献8中结论一致)。此外,喷射角较小有利于通过优化截面形状进一步提高尾梁升力。
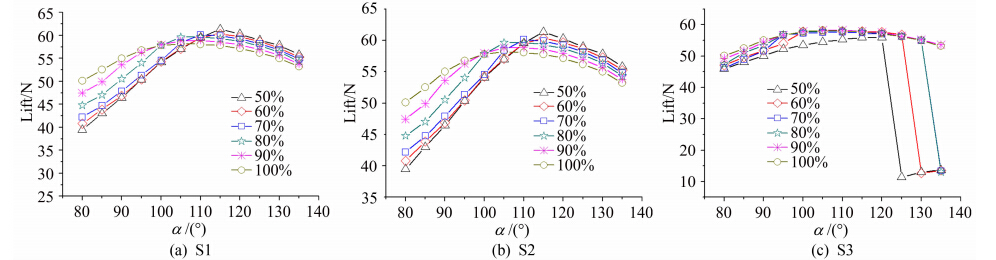 |
| 图 7 M2模型不同截面升力随狭缝迎角变化曲线(γ=30°)Fig. 7 Variation of different section lift force of M2 model with slot angle of attack(γ=30°) |
图 8中显示模型(M3)的下洗流速度为30m/s。从图中可以看出:① 由于沿尾梁壁面曲率的影响,S1截面较其它截面能够推迟气流分离,这使较低似圆度截面产生了明显的更高的极限升力;② S2截面在125°狭缝迎角之前升力随似圆度升高而升高,但在125°狭缝迎角之后升力随似圆度升高而下降;③ 提高下洗流速度容易引起气流分离[13],同时由于曲率相对更大,S3截面容易在水平轴位置引起气流分离,导致S3截面形状的极限升力低于圆截面。通过与基准组的对比发现,提高下洗流速度有利于提高环量控制尾梁的升力[13],也有利于通过优化截面形状进一步提高升力。
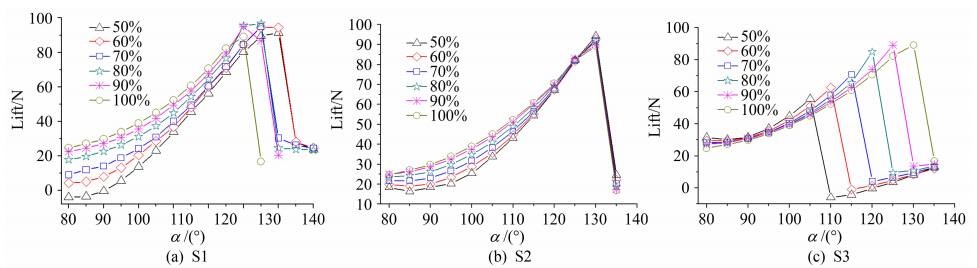 |
| 图 8 M3模型不同截面升力随狭缝迎角变化曲线(v∞=30m/s)Fig. 8 Variation of different section lift force of M3 model with slot angle of attack(v∞=30m/s) |
图 9中显示模型(M4)的喷射气流速度为108m/s。 从图中可以看出三种截面所产生的升力分别随着各自似圆度的升高而升高。与基准组的计算结果对比可以发现,提高狭缝喷气速度可以提高环量控制尾梁的升力[13]并会使最大升力狭缝迎角提前,但是对最优截面形状的影响较小。
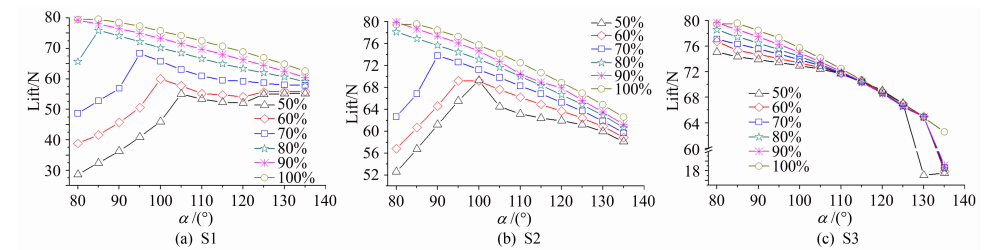 |
| 图 9 M4模型不同截面升力随狭缝迎角变化曲线(vjet=108m/s)Fig. 9 Variation of different section lift force of M4 model with slot angle of attack(vjet=108m/s) |
图 10显示的模型(M5)的外径为300mm。从图 中可以看出各截面的升力变化趋势与基准组类似,但直径增大后存在较多S1截面和S2截面优于圆截面, 也就是说,增大基准圆直径,有利于提高截面形状的优化空间。
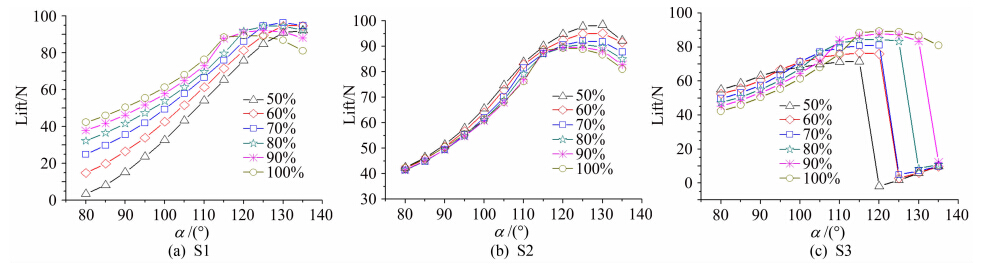 |
| 图 10 M5模型不同截面升力随狭缝迎角变化曲线(Φ=300mm)Fig. 10 Variation of different section lift force of M5 model with slot angle of attack(Φ=300mm) |
图 11显示的模型(M6)具备缝间角为40°的两条宽为0.5mm的狭缝。从图中可以看出存在多种截面形状的最大升力高于圆形截面的最大升力。与基准组作对比可以发现,增加一条狭缝有利于环量控制尾梁的升力更加平稳,对圆形截面尤其如此。
 |
| 图 11 两狭缝M6模型不同截面升力随狭缝迎角变化曲线(Ht=0.5mm×2,β=40°)Fig. 11 Variation of different section lift force of M6 model with slot angle of attack(Ht=0.5mm×2,β=40°) |
图 12所示模型(M7)的缝位角为80°。通过与M1模型的结果对比可以看出修改缝位角可以修改曲率大的位置相对于狭缝的位置,因而对附壁气流的稳定性有较大影响,通过优化缝位角可以较大程度地提高环量控制尾梁的最大升力。
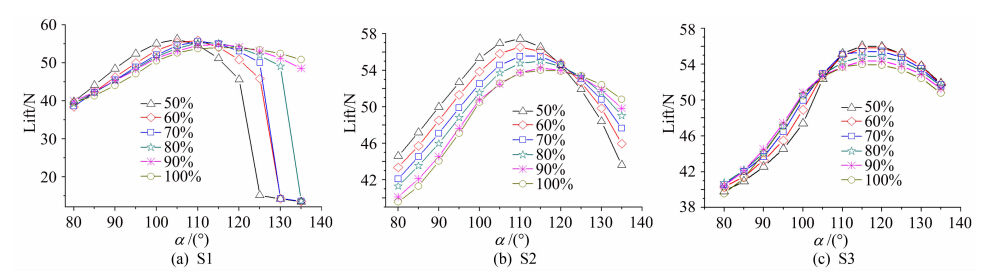 |
| 图 12 M7模型不同截面升力随狭缝迎角变化曲线(θ=80°)Fig. 12 Variation of different section lift force of M7 model with slot angle of attack(θ=80°) |
由于旋翼下洗流速度取决于主旋翼及直升机的工作状态,在环量控制尾梁基准直径已经达到合理较大值后,通过尽量减小狭缝喷射角、根据具体工作状 态优化缝位角和尾梁截面形状可以实现环量控制尾梁在同等功率消耗下产生接近于极限的升力,基于这 样的思路设计了模型M8。
图 13所示的模型(M8)的缝位角为80°、下洗流速度为30m/s,狭缝为圆弧形从而将喷射角减小到10°。从计算结果中可以看出在各种形状的截面中,圆形截面的性能并不突出。由于综合了缝位角、喷射角和下洗流速度对截面形状的影响,M8模型的最优截面形状性能相对于圆截面有较大程度的提高。
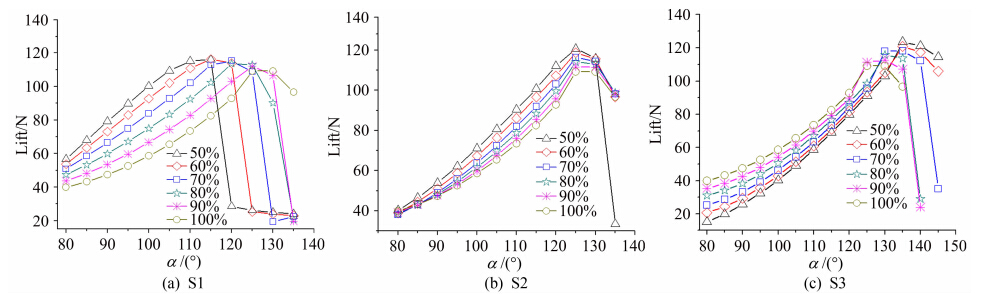 |
| 图 13 弧形狭缝,θ=80°,v∞=30m/s,γ=10°(M8)Fig. 13 Arcs profiled slot,θ=80°,v∞=30m/s,γ=10°(M8) |
为了便于进行归纳总结,将8个模型的模拟计算 结果统计后列于表 3中。表中最大升力比值指本组模型中所有截面的最大升力与圆截面最大升力之比。 我们对比了下洗流速度相同的M8模型和M3模型,由于减小了喷射角、优化了缝位角和截面形状,M8 模型产生的最大升力较M3模型圆截面产生的最大 升力提高了38.6%。保持其它几何和工作条件相 同,仅通过优化截面形状,M8模型的最大升力较圆截面的最大升力提高了13.2%。由此可见优化环量控制尾梁的狭缝形状和截面形状对提高环量控制尾梁性能的重要意义。
| 模型 | 最大升力截面 | 最大升力比值 | 最优截面 | 最优狭缝迎角 |
| M1 | 90%S1 | 1.006 | 90%S1 | 115°~125° |
| M2 | 50%S2 | 1.054 | 50%S2 | 110°~120° |
| M3 | 80%S1 | 1.084 | 60%S1 | 130°~140° |
| M4 | 90%S2 | 1.004 | 100% | 80°~90° |
| M5 | 50%S2 | 1.100 | 50%S2 | 120°~130° |
| M6 | 60%S1 | 1.076 | 70%S1 | 110°~120° |
| M7 | 50%S2 | 1.064 | 50%S2 | 110°~120° |
| M8 | 50%S3 | 1.132 | 50%S3 | 135°~145° |
图 14显示了不同截面形式最大升力截面和最大升力圆截面之间的速度分布和流线对比。
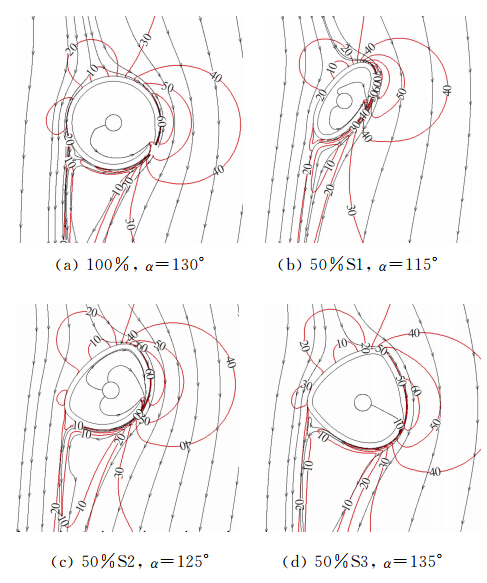 |
| 图 14 M8典型截面及状态近壁面气流速度分布及流线图Fig. 14 Velocity distribution and streamline of flow close to surfaces of typical cross sections of M8 |
图 14(a)中可以看出,在喷射气流的作用下附壁气流顺时针方向的绕流区域远大于逆时针绕流区域,
增大沿壁面的环量,从而产生了升力。而非圆截面本身的形状可以引导附壁气流在设计的位置脱离壁面,可以进一步扩大图 14中顺时针绕流的区域,提高尾梁产生的升力。S1截面在无射流时可以看作传统的对称翼型,在迎角未达到发生失速之前本身就可以产生升力,而喷射气流则可以增大其迎角使下洗流在翼型的前缘分流点 向逆时针方向侵占,增大顺时针流动附壁气流的区域和流动速度,提升升力。S2截面可以看作传统的非对称翼型,在迎角为零时即可能产生升力。实 际上,由于厚度过大,即使迎角为0°,也可能发生失 速,喷射气流同样可以引导附壁气流,使两侧气流交汇后脱离壁面,增大升力。与S2截面相似,由于S3截面在水平轴位置曲率较大,更容易用以发生气流分离,需要气流喷射角度更小、速度更大。
图 14中三个非圆截面垂直轴的左侧完全相同,右侧部分垂直轴两端间的路程长度和曲率不同,由此也导致了附壁气流的速度也有所区别,在各种因素的共同作用下,这三种截面的升力由小到大的次序分别为圆截面、50%S1、50%S2和50%S3。
4 结 论通过利用非圆截面形状的特点,特别是优化缝位角,可以增强附壁气流的稳定性,并引导其在适当的位置脱离壁面,明显提高尾梁的升力。
喷射角较小、下洗流速度较大以及基准直径更大有利于提高环量控制尾梁截面形状的优化潜力。
结合文献[13]的结论,整个环量控制尾梁的优化方向是尽量增大截面的基准直径、采用弧形狭缝从而最小化喷射角、采用双狭缝或多狭缝并适当增大缝宽从而将压缩空气尽量用于效率更高的环量控制尾梁、优化截面形状和缝位角,引导附壁气流在适当的位置脱离壁面。
| [1] | National Transportation Safety Board. Brief of accident[R]. File No.1848 Washington, DC 20594. |
| [2] | National Transportation Safety Board. Brief of accident[R]. File No.19201 Washington, DC 20594. |
| [3] | National Transportation Safety Board. Brief of accident[R]. File No.19745 Washington, DC 20594. |
| [4] | Fisher D T. Wind tunnel performance comparative test results of a circular cylinder and 50% ellipse tail boom for circulation control anti-torque applications[D]. California Monterey:NAVAL Postgraduater School, 1994. |
| [5] | Sampatacos E P, Morger K M, Logan A H. NOTARTM:The viable alternative to a tail rotor[C]//AIAA Aircraft Design, Systems and Technology Meeting. Fort Worth, Texas:American Institute of Aeronautics and Astronautics, 1983. AIAA-83-2527. |
| [6] | Conner D A, Burley C L, Smith C D. Flight acoustic testing and data acquisition for the rotor noise model (RNM)[C]//AHS 62nd Forum. Phoenix AZ:2006. |
| [7] | Oliver Maj R G, Belte D. letters of effort, government pilot evaluation of OH-6A/NOTAR[R]. USAAEFA Project No.83-08, 1983. |
| [8] | Morger K M, Clark D R. Analytic and experimental verification of the NOTARTM circulation control tail boom[C]//American Helicopter Society 40th Annual Forum. Arlington, VA:American Helicopter Society, 1984:419-428. |
| [9] | Holz R, Hassan A, Reed H. A 2-D numerical model for predicting the aerodynamic performance of the NOTARTM system tailboom[C]//American Helicopter Society 48th Annual Forum. Washington, D.C.:American Helicopter Society, 1992:1295-1305. |
| [10] | Tadghighi H, Thompson T L. Circulation control tail boom aerodynamic prediction and validation[C]//American Helicopter Society 45th Forum, Boston Massachusetts:American Helicopter Society, 1989:579-590. |
| [11] | Wang Huaming, Zhang Chenglin, Luo Xiaoping. Experimental study on no tail rotor (NOTARTM) helicopter[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2001, 18(1):54-59. |
| [12] | Wood N, Nielsen J. Circulation control airfoils past, present, future[C]//AIAA 23rd Aerospace Sciences Meeting. Reno Nevada:American Institute of Aeronautics and Astronautics, 1985. AIAA-85-0204. |
| [13] | LI Jiachun, Yang Weidong, Gao Ning. A parameter analysis of circulation control circular cylinder for NOTARTM tail boom[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2013, 30(3):282-291. |
| [14] | Winn A L, Logan A H. The MDHC NOTARTM system[C]. The RAE Conference for Helicopter Yaw Control Concepts. London:February, 1990. |
| [15] | Logan A H, Moore R E. Helicopter antitorque system using circulation control:USA, applications, 4200252[P]. 1980. |
| [16] | Carson F D. Antitorque and yaw control system for a rotary-wing aircraft:USA, applications, 6755374 B1[P]. 2004. |
| [17] | Luo Xiaoping, Zhang Chenlin, Shen Mongshan. Experimental study of circulation control tail boom[J]. Acta Aerodynamica Sinica,1996, 14(4):387-393.(in Chinese)罗小平, 张呈林, 沈梦山. 环量控制尾梁实验研究[J]. 空气动力学学报, 1996, 14(4):387-393. |
| [18] | Dong Zhenxing, Gao Yadong, Wang Huaming. Influence of circulation control parameters on lateral thrust of helicopter tail boom in rotor downwash[J]. Helicopter Technique, 2011, 169(4):12-15.(in Chinese)董振兴, 高亚东, 王华明. 直升机环量控制尾梁参数对直升机尾梁侧向推力的影响[J]. 直升机技术, 2011, 169(4):12-15. |