临近空间(距地面20km~100km的空域)既不属于航空范畴,也不属于航天范畴,对于情报收集、侦察监视、预警探测、通信保障及对空对地作战等军事应用潜力巨大,尤其是近空间低层(18km~25km)的平流层,由于气流稳定且常年风速较低,很适合低速超长航时飞行[1, 2, 3]。 目前国内外在研的临近空间超长航时飞行器系统主要有两大类,即“太阳能无人机”和 “平流层 飞艇”,这两类飞行器各自有其优势,但也存在显著缺点。太阳能无人机的优点是成本较低、机动 [CM(22*2]能力较强、可控性好,缺点是有效载荷能力小、升空速度慢、大展弦比和结构重量限制造成气弹效应显著,升空过程中复杂的气流条件会增加机翼失稳的危险;平流层飞艇优点是有效载荷大、升空速度较快、高空驻留较为容易,缺点是体积庞大、成本高、能耗大、飞行操控困难、机动能力较弱[4, 5, 6, 7]。
临近空间升浮一体飞行器,它将传统高空飞艇和太阳能无人机两者的优势结合起来,即将动力飞行器和静力飞行器的优点组合在一起,以求在几何尺寸增加不多的情况下,发挥浮力体与气动体共同的优势,提供比常规飞艇数倍至数十倍的有效载荷能力。例如盘翼式升浮一体飞行器可由浮力、空气动力和反作用力三者共同提供升力,不仅有效载荷大,而且飞行性能好,经济效益优于飞艇和飞机,见图 1[3]。
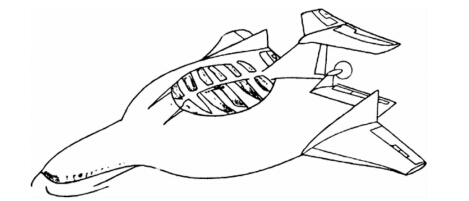 |
| 图 1 盘翼式升浮一体飞行器Fig. 1 Discal wing buoyancy-lifting vehicle |
升浮一体飞行器按照布局特点又可细分为飞航式和飞艇-直升机混合式两种,如图 2所示。飞航式升浮一体飞行器通过给飞艇加装机翼或把艇体几何外形变成更有效的升力体外形的方式以寻求加强气动升力的能力。飞航式升浮一体飞行器就像飞机一样,依靠气动升力就可以承受相当一部分比例的载荷。由于气动升力的存在,这些浮升一体飞行器在起降时需要一定的地面进行起跑操作,同时这也使地面控制和操作要比常规布局飞艇简单安全许多[8, 9, 10]。
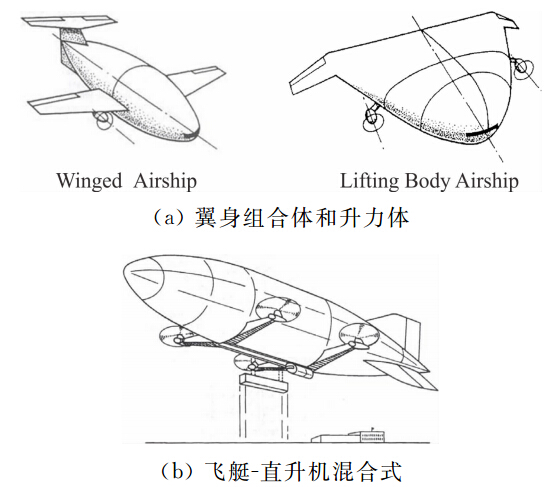 |
| 图 2 升浮一体飞行器示意图Fig. 2 Configurations of buoyancy-lifting vehicle |
本文结合高空飞艇和太阳能无人机气动布局的特点,提出一种可用于临近空间飞行的升浮一体飞行器布局,见图 3所示。
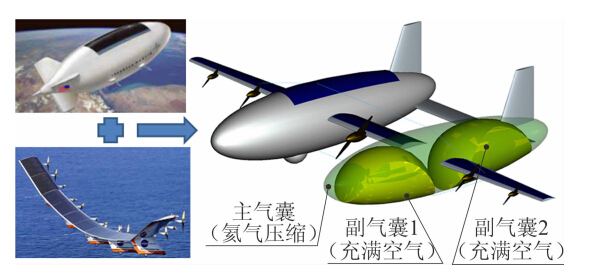 |
| 图 3 升浮一体飞行器Fig. 3 Buoyancy-lifting vehicle |
该布局采用大容积率高升阻比气动外形和轻质复合材料机体结构,巡航时靠浮力和升力平衡重力,其中浮力部分约占55%,升力部分约占45%。机身采用软式主副气囊结构,蒙皮采用轻质、高强度、高耐候性、低渗透率的复合材料,机翼采用复合材料的翼梁、翼肋和蒙皮一体的刚性结构或充气翼结构,刚性机翼与机身的连接采用轻质复合材料框架和斜拉索结构;飞行控制系统综合利用副气囊、气动舵面和推力矢量构成操控系统,实现飞行器从地面自主垂直起降、稳定爬升、高空巡航、抗风和机动等功能;使用高效太阳能电池和高能量密度储能电池及能源管理系统构成能源系统提供白天和越夜动力系统、机载设备和有效载荷所需能量;使用多台不同功率的稀土永磁直流无刷电机和轻质高效螺旋桨构成推进动力系统,以适应低空起降、爬升、高空巡航、降高越夜、机动飞行等不同任务对动力系统的指标要求。
针对升浮一体飞行器布局特点,应用理论方法和数值模拟方法开展气动布局设计研究,并且对设计结果进行风洞实验验证。 1 气动布局设计 1.1 气动布局设计方法 1.1.1 理论方法
临近空间升浮一体超长航时太阳能无人机的阻力来源主要是机体和机翼,机体的阻力主要来源于压差阻力和摩擦阻力两部分,长细比:λ是影响机体阻力特性的重要几何参数。长细比越大压差阻力越小,另一方面,长细比越大,在体积相同的条件下表面积越大,带来了更大的摩擦阻力[11, 12]。
经典理论推导表明,传统的艇身外形在长细比λ=4.65时,阻力系数最小,因此,在早期飞艇设计中,为使飞艇受到较小的阻力,长细比常取为4~6 之间,阻力系数在0.02~0.03 之间。此处在估算机体阻力时,参考S. F.Hoerner 经过理论推导得到的长细比对艇身阻力系数的影响关系式(1)和在湍流条件下通过试验数据拟合得到的式(2)来计算。
式中:CDV 为阻力系数(参考面积基于机体体积的2/3次方);CF为基于机体表面积的摩擦力系数,ReL 为基于机体长度的雷诺数[13]。机翼的阻力分为零升阻力CD0和诱导阻力CDi两部分,使用工程经验公式(3)和经典理论公式(4)估算,式中:CL为升力系数;e为机翼效率因子,对于大展弦比机翼通常取0.85~0.9;Ar为机翼展弦比[14]。
气动布局设计采用分部件的方式进行,大容积的机体主要提供全机所需升力中的静升力,设计时以低摩阻、低压阻和大容积面积比为目标,以机体长细比为约束,通过前面提及艇身的工程估算方法,建立机体气动布局的快速设计方法。
大展弦比的机翼主要提供全机所需升力中的动升力,设计时以巡航迎角附近高升力、高升阻比为目标,以机翼展弦比、翼型气动性能和翼型最大相对厚度为约束。通过工程经验估算零阻以及面元法[15]计算升力系数和诱导阻力系数,建立机翼气动布局的快速设计方法。
气动安定面设计参考低速飞行器的设计准则和统计的无量纲化设计参数(通常所提及的尾容量系数,在此称为安定面容量系数),设计时以良好的稳定性、操纵性为目标,以安定面容量系数和安定面摩阻为约束,建立安定面的选型设计方法,同时结合优化设计方法,完成安定面的选型设计。
应用上面介绍的各部件气动力评估方法,组合起来建立全机气动评估的理论方法。
1.1.2 数值方法采用自主研发的CACFD计算流体力学软件平台作为数值模拟方法评估工具(简称CFD方法)。
计算网格全部为分区结构网格。采用理想气体模型,湍流模型采用标准S-A模型,SIMPLE算法。网格设计如图 4所示,为升浮飞行器布局表面网格。
气动设计时,其主要的矛盾体现在高升阻比气动特性和大展弦比机翼结构、高升阻比气动特性和稳定性/操纵性之间的综合协调,在结构设计预期指标和飞行控制设计预期指标无法满足的情况下,高升阻比的气动性能会低于预期,从而给能源和推进系统带来影响,一旦出现这种情况,只能在升阻比尽可能下降不大的基础上,适当地降低机翼的展弦比以满足结构设计的要求,适当地增加安定面和操纵面的面积使稳定性/操纵性能满足飞行控制的要求;此外还需调整飞行空域、飞行速度和留空时间等,待结构设计和飞行控制设计达到预期指标后再进行调整到预期的使用设计要求。
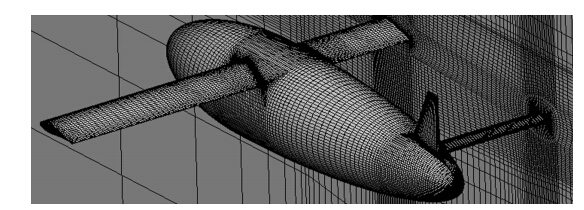 |
| 图 4 升浮一体飞行器表面网格(半模)Fig. 4 The wall grid on buoyancy-lifting vehicle(half-model) |
临近空间升浮一体超长航时太阳能无人机采用双机身+平直翼+平尾+双垂尾气动布局。经过多轮设计评估改进后的布局尺寸如表 1所示,初始外形和改进后外形见图 5所示。
 |
| 图 5 改进前后升浮一体气动布局对比Fig. 5 Comparison of configuration before and after improvement |
| 翼面积/m2 | 展长/m | 机身容积/m3 | 机身半径/m | 机身长度/m |
| 293.4 | 66.3 | 2039.4×2 | 4.71 | 42.4 |
机身采用NPL低阻力系数飞艇艇身外形,长细比λ=4.50。该外形由英国国家物理实验室提出。沿着对称轴的横截面由数学公式确定,由公式确定的形状如图 6所示,从艇首到艇尾曲率半径增大,从而减小气流分离的可能性。
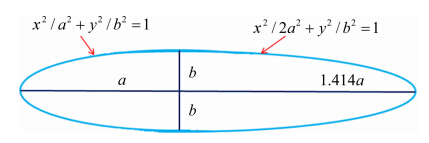 |
| 图 6 NPL低阻艇身外形Fig. 6 Configuration of NPL air cell with low drag |
机翼翼根采用EPPLER398翼型,厚度为14.2%,安装角为4.0°;翼稍采用EPPLER396翼型,厚度为13.1%,安装角为2.0°;机翼根稍比1.5,参考展弦比15。平尾和垂尾均采用NACA0012翼型;平尾根稍比2,安装角为2.5°;垂尾根稍比2。
采用上述的工程方法和CFD方法对升浮一体布局进行气动计算,设计点为巡航高度20km,飞行速度为31.5m/s。结果如图 7、图 8所示。从图 5可以看出,升力系数在-2°攻角时基本重合,随着攻角的增加两种方法得到的升力系数差值逐渐增大。这是因为工程计算中还无法计算艇身的升力系数以及兼顾机翼与艇身组合的气动影响,而CFD方法的计算结果则包含艇身的升力系数,并且可以模拟机翼与艇身组合的气动影响。因此计算升力的计算结果存在一定的误差,而两种方法得到的升力线斜率结果分别为0.120和0.160,相差25%。
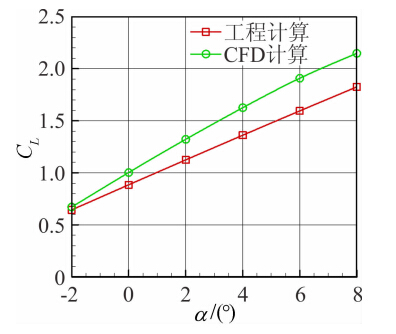 |
| 图 7 升力系数随攻角变化曲线Fig. 7 Comparison of lift coefficient between engineering method and CFD of deferent attack angles |
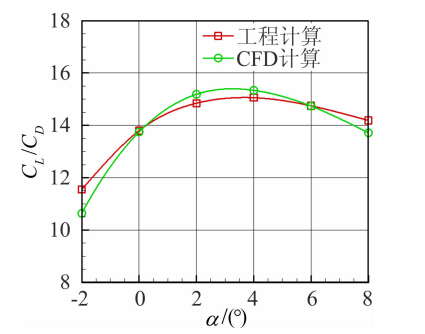 |
| 图 8 升阻比随攻角变化曲线Fig. 8 Comparison of lift-drag ratio between engineering method and CFD of deferent attack angles |
从图 8得出两种方法获得的升阻比基本上接近,工程方法获得的最大升阻比为15.06,CFD方法获得最大升阻比为15.34,对应的攻角均为4°左右。这是因为工程计算中还无法计算艇身的压差阻力,只能计算艇身的零升阻力,因此工程方法获得布局的阻力系数偏低。以上结果表明本文提出的气动布局设计方法是合理的。 2 风洞实验[16] 2.1 实验设计
临近空间环境中空气的密度和湍流度对风洞实验相似性具有重要影响。临近空间空气密度很小,20km高度大气密度只有海平面的1/14。按照设计点(巡航高度20km,飞行速度31.5m/s)机翼的工作雷诺数约为8.01×105。由于模型是双机身布局,且机翼厚度较小以及无法安装内埋式天平,因此决定采用外式张线天平作为实验模型的测量系统。
根据风洞性能指标取气流速度为v=30m/s、50m/s和70m/s,对应基于机翼平均气动弦长的自由流雷诺数分 别为Re=2.27×105、3.78×105和5.30×105。试验攻角范围:-6°~14°,侧滑角范围:-5°~20°。
本次实验选用1:40全金属模型,如图 9所示,用于气动力系数无量纲的主要几何参数见表 2。
 |
| 图 9 升浮一体布局模型安装在风洞Fig. 9 Model of Buoyancy-lifting Vehicle in wind tunnel |
| 参考面积 | 0.183125m2 |
| 纵向参考长度 | 0.1105m |
| 横向参考长度 | 0.1105m |
| 力矩参考点 | 模型头部,与天平校心重合 |
实验采用的风洞是一座单回流闭口低速风洞,试验段长14m,横截面为3m×3m四角圆化正方形,圆角半径为0.5m,试验段有效面积为8.785m2。风洞试验风速为10~100m/s无级调速。风洞流场品质良好,湍流度低于0.13%,平均气流偏角低于0.2°,试验段左右两侧洞壁互相平行,上下两侧洞壁沿流向各有0.2°扩张角,使得轴向静压梯度基本消除。
张线天平主要由下列部件组成:支架、张线系统、带有攻角机构的传力系统及测量元件、侧滑机构、地面效应试验用的地板及驱动系统、密封系统、数据采集、处理及模型姿态、地板高度控制系统。
2.3 实验方法张线天平测力实验主要包括如下几个步骤:
步骤1 安装和调整张线天平系统;
步骤2 天平综合加载、校测,检查天平、测试系统以及计算程序的正确性;
步骤3 安装模型,测量并计算模型力矩参考点与天平校心之间的距离;
步骤4 调整模型初始状态角,如攻角、侧滑角及滚转角都要调整到0°,一般误差在3′以内;
步骤5 正式实验。正式实验时模型正装于风洞中,低头为正攻角。实验过程中固定动压、侧滑角,按照给定的攻角阶梯改变攻角进行实验。当风速稳定后采集数据保存,原始数据包括天平六分量数据,以及攻角、侧滑角和动压的测量数据。每完成一个测量车次后即对实验数据进行现场处理与分析。
2.4 数据处理由于天平测量的零点数据是在某一模型状态下的,当模型状态改变时(主要是攻角变化时),模型的自重分量(法向分量、轴向分量、俯仰力矩分量)随之改变,对天平的作用力也就发生了变化,因此必须进行自重修正。具体方法是:在停风状态下,采集某一模型状态的自重数据,而后在相应的吹风数据中进行扣除。
采用张线天平进行测力试验时,张线除了起到支撑模型的作用,同时还起到传递模型气动载荷的作用。在吹风时张线系统本身也会受到气动载荷作用,这部分气动载荷同样会传递到测量元件上而成为模型气动载荷的一部分,因此需要对张线系统本身受到的气动载荷进行扣除。具体做法是:在未安装模型的情况下,根据试验需要采集不同风速和侧滑角下的张线力,然后在相应带模型的吹风数据中进行扣除。需要说明的是张线力扣除准确与否对试验模型的阻力结果影响较大。 2.5 实验结果与分析 2.5.1 风速对纵向气动特性影响
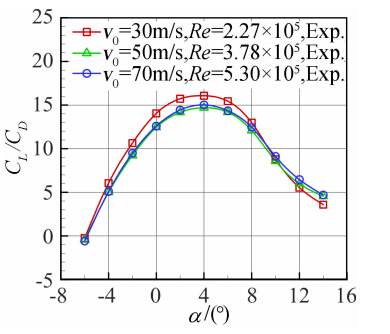
图 10~图 11给出了升浮一体飞行器模型在侧滑角0°、不同来流风速下的纵向气动特性曲线。从曲线图中可以看出,对于同一来流风速来说,在试验攻角-6°≤α≤4°范围内,升力系数CL随着攻角的增加基本呈线性增加,在攻角4°左右升阻比达到最大。从图 10,图 11中可以看出,随着雷诺数的增加,模型的升力系数和升阻比在大攻角时,不是增加反而减小。这是由于张线支撑机构的影响造成模型安装位置上方的洞壁存在一定的漏气,在外界大气压作用下,造成该处向模型吹气,从而减小模型的有效攻角,而且这种吹气速度随着风洞来流速度的增加而加大,特别是在大攻角时风洞的阻塞比增大以后,吹气的速度还进一步加大,这正是造成了模型在高雷诺数和大攻角状态下,气动系数反而减小的主要原因。
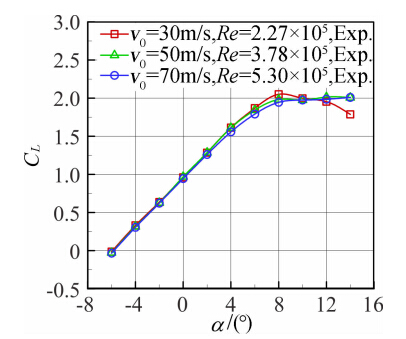 |
| 图 10 不同来流速度下升力系数随攻角的变化Fig. 10 Variation of lift coefficient with attack angles at different inflow velocity |
 |
| 图 11 不同来流下升阻比随攻角的变化Fig. 11 Variation of lift-drag ration with attack angles at different inflow velocity |
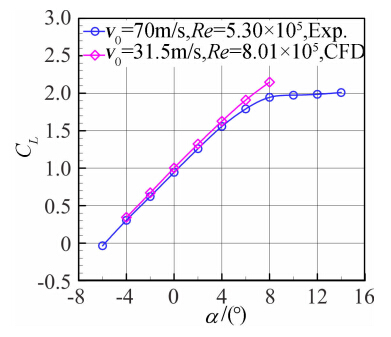
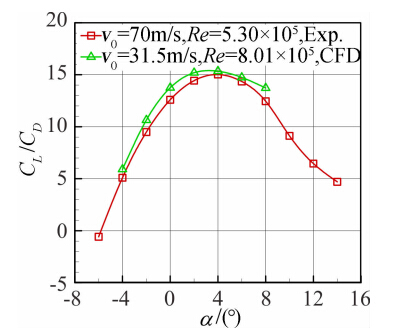
图 12给出升力系数CFD与实验结果的对比,-4°≤α≤-6°时,升力系数基本吻合。α>6°时,升力系 数相差增大,主要是由于CFD是全湍流计算,实验则 是自然转捩,造成两种模态的失速攻角不同,而且雷 诺数也存在一定差别。图 13表明,CFD计算结果与 实验结果的升阻比基本吻合,由于雷诺数的影响最大升阻比相差0.3左右。
 |
| 图 12 CFD和实验的升力系数结果对比Fig. 12 Comparison of lift coefficients between experiment and CFD |
 |
| 图 13 CFD和实验的升阻比结果对比Fig. 13 Comparison of lift-drag ratios between experiment and CFD |
表 3给出了不同来流风速下纵向气动参数对比。从表 3可以看出,不同来流风速下零升攻角、纵向静稳定度均比较接近,风速v=30m/s时,最小阻力系数CD0最小,最大升阻比Kmax最大;随着风速v从30m/s增加到70m/s,最大升力系数逐渐降低,失速攻角逐渐增加。风速v=70m/s时,升力线斜率CαL出现明显下降。总体看来在来流v=30~70m/s范围内,雷诺数对升力线斜率影响不大,变化在3%以内,与CFD计算的升力线斜率0.160基本接近,验证CFD气动布局设计方法的可靠性。
| v/(m·s-1) | CαL | CD0 | Kmax | CLmax |
| 30 | 0.1607 | 0.0545 | 16.07 | 2.0509 |
| 50 | 0.1625 | 0.0626 | 14.69 | 2.0147 |
| 70 | 0.1571 | 0.0597 | 15.02 | 2.0096 |
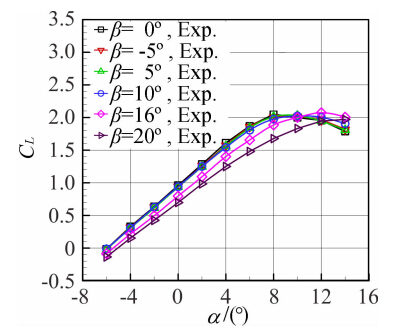
图 14~图 19分别给出了升浮一体飞行器布局模型在来流风速v=30m/s不同侧滑角下的纵横向特性曲线。从曲线图 14~图 16中可以看出,对于同一来流风速来说,在侧滑角|β|≤10°时,纵向气动特性基本比较接近,侧滑角大于10°后升力线斜率和纵向静稳定度出现明显下降,最小阻力系数明显增加。如图 17、图 18所示,随着侧滑角|β|从0°增加到20°,侧向力系数|Cz|和偏航力矩系数|Cmy|在全部试验攻角范围内随着侧滑角的增加而相应增加;侧滑角|β|≤5°时,在攻角-6°≤α≤8°范围内侧向力系数随攻角增加无明显变化;侧滑角β≥16°时,侧向力系数|Cz|和偏航力矩系数|Cmy|随攻角增加而增加。 从图 19可以得出-2°≤α≤2°,-5°≤β≤10°,横航向是稳定的,当攻角β≥10°,则出现不稳定。当攻角α≥4°时,横航向则在-5°≤β≤20°是稳定的。
 |
| 图 14 不同侧滑角时升力系数的比较Fig. 14 Comparison of lift coefficients at different sideslip angles |
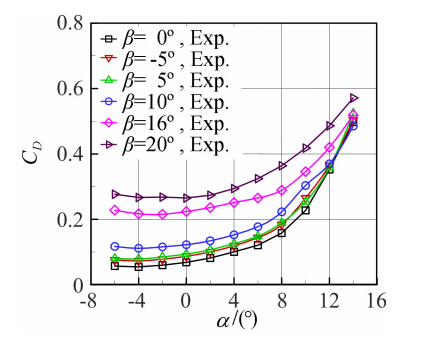 |
| 图 15 不同侧滑角时阻力系数的比较Fig. 15 Comparison of drag coefficients at different sideslip angles |
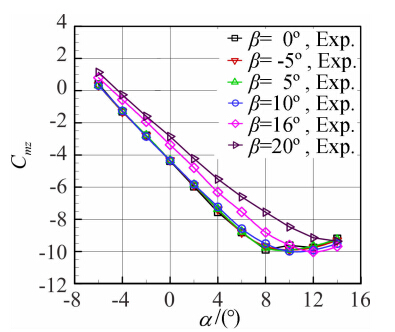 |
| 图 16 不同侧滑角时俯仰力矩系数的比较Fig. 16 Comparison of pitching moment coefficients at different sideslip angles |
从图 20可以看出,在侧滑角不为0的情况下,滚 转力矩系数|Cmx|随攻角增加而增加。滚转力矩系数 |Cmx|除了在攻角-6°≤α≤-2°范围之外均随着侧滑角的增加而相应增加,正负侧滑角的横航向特性曲线关 于β=0°时曲线基本对称,曲线规律性很好。
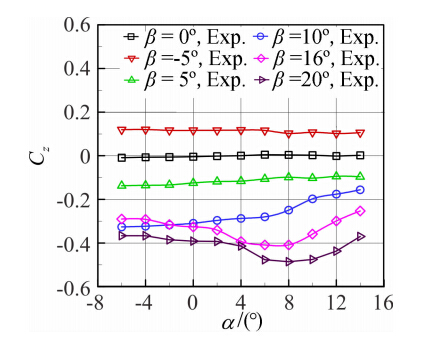 |
| 图 17 不同侧滑角时侧向力系数的比较Fig. 17 Comparison of lateral force coefficients at different sideslip angles |
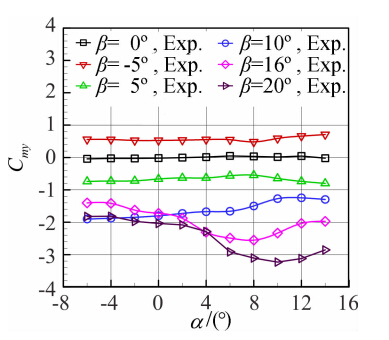 |
| 图 18 不同侧滑角时偏航力矩系数的比较Fig. 18 Comparison of yaw moment coefficients at different sideslip angles |
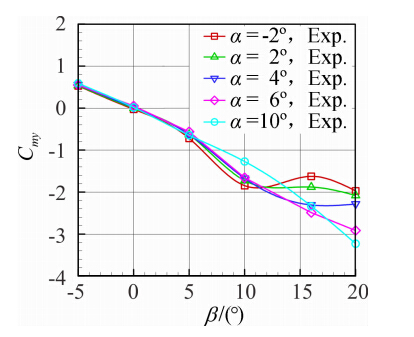 |
| 图 19 不同攻角下偏航力矩系数随侧滑角的变化Fig. 19 Variation of yaw moment coefficients with sideslip angles at different attack angles |
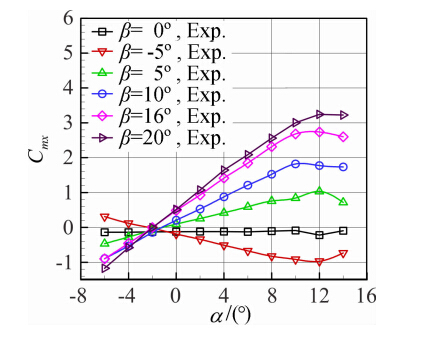 |
| 图 20 不同侧滑角时滚转力矩系数的比较Fig. 20 Comparison of rolling moment coefficients at different sideslip angles |
应用理论方法和数值模拟方法开展升浮一体布局气动设计研究,获得升阻比>15的升浮一体太阳能飞行器气动布局,并对设计布局开展实验验证研究,得出以下结论:
(1) 工程经验公式和面元法结合的可以满足临近空间升浮一体太阳能无人气动布局设计的快速选型的需求,设计升阻比结果与实验结果吻合良好。
(2) 由于工程方法和面元均无法评估艇身升力和压差阻力,因此快速气动布局设计方法获得升浮一体气动布局的升力系数和阻力系数均偏小,必须采用CFD方法进行修正。CFD方法计算的气动结果与实验结果相接近。验证张线天平测试多机身气动布局的可靠性。
(3) 来流v=30~70m/s范围内,雷诺数对升浮一体布局气动性能有一定影响。升力线斜率先增大后减小,变化在3%左右,与CFD计算的升力线斜率0.160基本接近。零升阻力也是先增大后减小,变化在10%左右。这主要是由于机翼上转捩位置变化引起的。
(4) 纵向气动特性研究结果表明:在侧滑角|β| ≤10°时,纵向气动特性基本接近,侧滑角大于10°后升力线斜率和纵向静稳定度出现明显下降,最小阻力系数明显增加。
(5) 横向气动特性研究结果表明:侧滑角|β|≤5°时,在攻角-6°≤α ≤8°范围内侧向力系数随攻角增加无明显变化;侧滑角β≥16°时,侧向力系数|Cz|和偏航力矩系数|Cmy|随攻角增加而增加。在小攻角和大侧滑角时,横航向出现不稳定 ,其它状态则都是稳定的。
(6) 滚转力矩系数|Cmx|除了在攻角-6°≤α≤-2°范围之外均随着侧滑角的增加而相应增加,正负侧滑角的横航向特性曲线关于β=0°时曲线基本对称,曲线规律性很好。
| [1] | Body R R. Performance of hybrid air vehicles[C]. 40th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2002. |
| [2] | Liu Tianshu, Lou W W. Aeroship:a new flight platform[C]. 24th AIAA Applied Aerodynamics Conference, San Francisco, CA, 2006. |
| [3] | 叶军科. 超高空飞艇的气动减阻与气动技术研究[D].[博士学位论文]. 西安:西北工业大学, 2008. |
| [4] | John H Del Frate. High altitude platform aircraft at NASA past, present and future[R]. York, UK, 2006. |
| [5] | Joner B A, Schneider J J. Evaluation of advanced airship concepts[R]. AIAA- 75-930, 1975. |
| [6] | Allen E H. The case for near space[J]. Aerospace America, 2006, (2):31-34. |
| [7] | Colozza A J. Initial feasibility assessment of a high long-altitude endurance airship[R]. NASA CR-2003-212724, 2003. |
| [8] | G. A. 库利 J. D. 吉勒特. 飞艇技术[M]. 王生, 等译. 北京:科学出版社, 2008. |
| [9] | Wang Yi. The development of the earth observation system[J]. Advances in Earth Science, 2005, 20(9):980-989. (in Chinese)王毅. 国际新一代对地观测系统的发展[J]. 地球科学进展, 2005, 20(9):980-988. |
| [10] | Qu Dongcai. Study an development of airship[J]. Aeronautical Science and Technology, 2005, (2):20-23. (in Chinese)曲东才. 飞艇研制及发展[J]. 航空科学技术, 2005, (2):20-23. |
| [11] | 宋笔锋. 超高空飞艇的发展现状和关键技术分析[J]. 航天航空技术, 2005, (2). |
| [12] | 甘晓华, 郭颖. 飞艇技术概论[M]. 北京:国防工业出版社, 2005. |
| [13] | Ren Yipeng, Tian Zhongwei, Wu Ziniu. Some aerodynamics problems of airship[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(3):431-443. (in Chinese)任一鹏, 田中伟, 吴子牛. 飞艇空气动力学及其相关问题[J]. 航空学报, 2010, 31(3):431-443. |
| [14] | 李为吉. 现代飞机总体综合设计[M]. 西安:西北工业大学出版社. |
| [15] | Mark Drela. AVL3.26 user primer[M]. MIT Aero. & Astro. Harold Youngren, Aerocraft, Inc., 2006. |
| [16] | 贾毅. SS模型低速风洞张线测力试验报告[R]. 北京, 2010. |




