0 引 言
战斗机历来是空中力量的中坚。未来先进战斗机为实现良好的敏捷性、大迎角过失速机动飞行、超短距起飞着陆性能等,要求飞机具有良好的操纵特性和机动性能,并要求在全飞行包线范围内都具有良好的升力和控制力矩特性。传统的通过操纵面偏转获得所需控制力和力矩的方法,已经难以满足高性能先 进战斗机的需求,采用推力矢量转向控制技术是实现上述目标的有效手段之一。
射流推力矢量控制技术是通过在喷管内型面引入次流,利用次流及其与喷管内主气流相互作用,使喷管主气流相对飞行器轴线发生偏转来实现推力矢量控制。与传统的机械式推力矢量控制技术相比,射流推力矢量控制技术具有机械部件少、重量轻、费用低、矢量角偏转速率高等显著优点[1],因而已引起航空领域的广泛关注。目前研究较多的射流推力矢量控制技术主要有:激波控制、喉道偏斜以及在此基础上发展的双喉道偏斜和逆流控制等。激波控制可以产生较大的推力矢量角,最大可达17.3°,但由于主流通过激波,推力系数损失较大(典型的为0.84~0.90)[2, 3]。喉道偏斜可以产生较大的推力系数(可达0.94~0.98)[4, 5, 6],但产生的推力矢量角比激波控制小。逆流控制使用较小的射流就能产生较大的矢量角,推力系数也较高,但可能存在的附着效应和真空源是其急需解决的问题[7, 8, 9]。双喉道射流推力矢量喷管(DTN)是NASA LaRC于2003年提出的一种新的射流推力矢量喷管概念[4]。DTN是在传统的喉道偏斜喷管后增加一个收缩段,形成凹腔,在上游喉道引入射流偏转该处的声速面,通过凹腔内流动分离产生的上下壁压力差进一步偏转主流(见图 1)。同样条件下,双喉道喷管比喉道偏斜喷管能产生更大的推力矢量效率,且推力系数不降低。NASA在此方面开展了较多研究[4, 10, 11, 12, 13, 14, 15, 16, 17, 18],并详细分析了二元和轴对称DTN的内流特性和矢量控制效果。国内目前对DTN的研究尚处于探索跟踪阶段,还未形成真正的工程实用能力,已有的初步研究结果表明DTN在获得高推力系数的同时,实现了高推力矢量效率,显示了DTN在推力矢量控制技术应用方面具有广阔的前景。
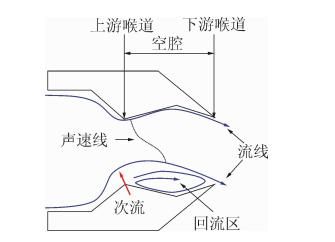 |
| 图 1 DTN的工作机理图Fig. 1 Sketch of the dual throat nozzle |
本文采用数值模拟方法对DTN在非推力矢量和推力矢量下的内流特性和推力矢量控制效果进行了详细研究,并探讨了喷管流动参数对DTN内流特性及推力矢量性能的影响。 1 DTN模型和主次流条件参数
本文DTN研究模型[13]如图 2所示,该模型是一个有两个喉道的二维收缩-扩张-收缩喷管,在两个喉道之间有一个“空腔”。喷管的宽度101.6mm,上、下游喉道的理论高度29.21mm,上、下游喉道的理论面积约为2967mm2。空腔长度为76.2mm,空腔的扩散角为-10°,收敛角为20°。射流出口位于上游最小喉道附近,入射角度为150°。
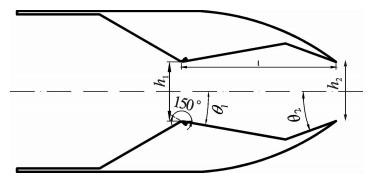 |
| 图 2 DTN几何外形Fig. 2 Geometrical configuration of DTN |
本文研究中,DTN主流落压比(NPR)范围为2~7,次流流量比范围为0%~6.5%,流体介质均为空气。 2 网格划分及数值方法
DTN二维计算区域从喷管出口截面向下游延伸了125倍喉道高度,向前延伸了30倍喉道高度,向两侧延伸了50倍喉道高度。计算模型的局部网格划分见图 3。为提高计算精度及效率,采用结构化网格,为减小网格生成难度,提高网格质量,计算域被分为16个子区,各子区网格单独生成后进行对接形成计算域。在上下壁面加密,离壁最近的网格单元y+在0.5附近,网格总数约10万。
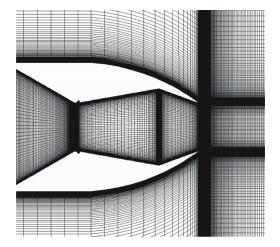 |
| 图 3 DTN局部网格划分Fig. 3 Enlarged view of the grid near DTN |
本文在数值模拟中,控制方程为全N-S方程组,湍流模型为RNG k-ε模型,在壁面附近采用增强壁面处理,流动方程及湍流模型的对流项采用二阶迎风格式,扩散项采用中心差分格式。计算边界条件给定 如下:外流场选取压力远场边界条件,静压为101 325Pa, 总温固定为300K,自由来流马赫数选取为0.05,以 便于计算收敛;喷管进口为滞止参数条件,给定总压,总温300K,速度方向沿边界法向;次流腔进口为滞止参数条件,给定总温300K,总压在计算中调整以使次流流量比恒在某个值附近;其它边界均为无滑移绝热固壁边界。计算中,次流均从下方的次流腔中注入,上方的次流腔关闭。计算的收敛性根据残差下降量级、喷管出口流量来综合判断。当计算残差下降3个数量级以上,且出口流量长时间保持恒定时,认为计算收敛。 3 DTN性能参数计算公式 3.1 各等熵推力的计算
主流等熵推力:
Fi,p=44.825wp [(1-NPR-2/7) Tt,p]1/2
次流等熵推力:
Fi,s = 44.825ws[(1- (NPR·SPR)-2/7) Tt,s]1/2
系统等熵推力:
Fi,sys=Fi,p+Fi,s 其中,wp、ws分别为主、次流质量流量,NPR、SPR分别为主、次流压比,Tt,p、Tt,s分别为主、次流总温。 3.2 等熵流量的计算
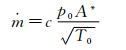
内推力的积分形式为:
F =∑ ρ v ·( v · n )+(p-pa)· n ·ΔA
在三维坐标系下,有:
Fx=∑[ρuun+nx(p-pa)]·ΔA
Fy=∑[ρvun+ny(p-pa)]·ΔA
Fz=∑[ρwun+nz(p-pa)]·ΔA 其中, n 为喷管出口面的外法线,v 为出口面上的速度矢量,un为法向速度的大小,un=unx+vny+wnz。在喷管出口面按上式积分获得喷管内推力的各分量,而后按下式计算喷管产生的实际总推力:
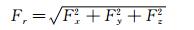
系统推力系数: Cfg,sys=Fr/Fig,sys
推力矢量角: δp=arctg(Fy/Fx)
次流流量比: ω=ws/wp
推力矢量效率: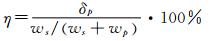 4 计算结果分析
4.1 数值方法实例验证
4 计算结果分析
4.1 数值方法实例验证
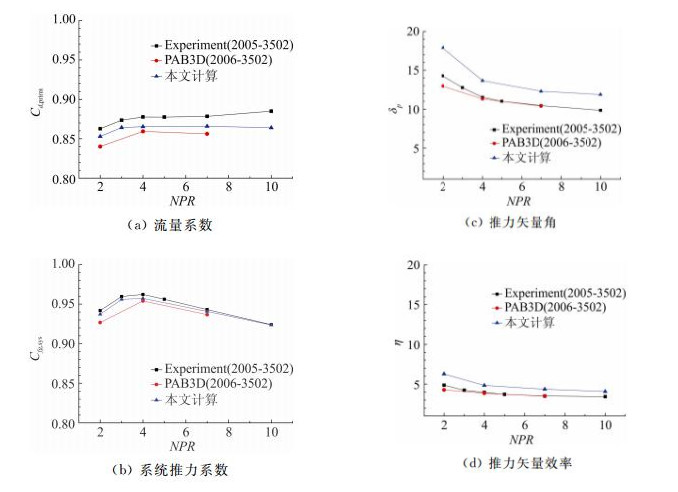
图 4给出了无射流DTN喷管流量系数Cd,prim,推力系数Cfg,sys试验结果、PAB3D计算结果[13]与本文计算结果的对比曲线图。可见,计算结果同试验结果基本吻合,系数随NPR变化趋势基本相同,表明本文采用的数值方法基本正确。
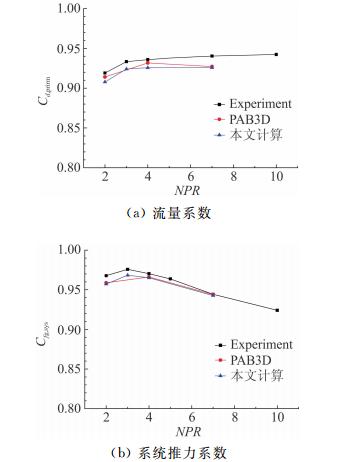 |
| 图 4 无射流DTN内流特性参数对比图Fig. 4 Comparison of the internal flow patterns obtained by experiments and computations |
4.2 次流流量比3%、NPR=4时DTN的内流特性
以主流落压比为4、次流流量比为3%工况为例对喷管流动状态进行分析。图 5给出了喷管流线图和等马赫数线图。从图中可看出,喷管内主流发生了两次偏转:第一次发生在上游喉道附近,由于次流的注入压迫喷管主流向上偏转;第二次发生在下游喉道附近,由于空腔收敛段的导流作用所致。主流两次偏转的最终效果使得喷管出口处气流以一定的角度排出,从而使喷管获得矢量推力。由于次流的注入,导致了管内流动的非对称性和DTN下部很大的分离 区,分离区的上边界外凸,形成了主流的“流动边界”,使得主流在几乎不扩张的通道内流动,马赫数基本在1以内,只在喷管的出口气流才达到声速。由于主、次流的掺混在低马赫数下进行,在管内的超声速区不大,没有强烈的激波系,避免了较大的推力损失。
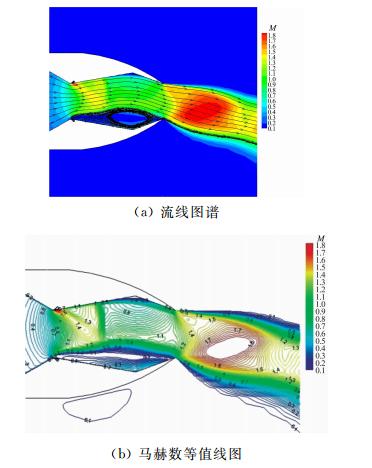 |
| 图 5 DTN马赫数及流线分布图(NPR=4,次流流量比3%)Fig. 5 Mach contours and streamlines of DTN (NPR=4,secondary flow injection flowrate 3%) |
图 6为喷管流场静压线图。从图中可以看出,喷 管入口段流速较低,内部静压对称且较高,接近喷管主流总压值;气流进入喷管收敛段后,由于速度增加,气流压力随之下降,且随着喷管轴向距离的增加逐渐呈不对称状,这是由于次流的干扰所致。在喷管空腔 内部,静压基本维持在250kPa附近;在喷管空腔上 下转角处,由于气流在此流速较低,静压有一定程度的提升。在气流流经下游喉道的过程中,由于气流流速增大,压力逐渐降低,一直延伸至喷管出口处。
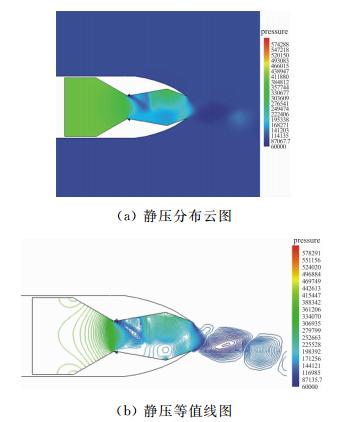 |
| 图 6 DTN静压分布图(NPR=4,次流流量比3%)Fig. 6 Static pressure contours of DTN (NPR=4,secondary flow injection flowrate 3%) |
图 7给出了DTN上、下壁面静压分布曲线以及相同参数下次流流量为0的壁面压力分布,从图中可以看出沿喷管壁面静压的变化过程。在非推力矢量下,DTN的上 下壁面压力分布是对称的,但是在推力矢量下,下壁面附近由于大分离区的出现,导致了整个下壁面压力都比较低。次流流量比为3%的壁面压力分布显示在喷管进口段,静压值较高且变化不大,上、下壁面压力值相等。在接近喷管上游喉道时,上、下壁面静压迅速下降,因下壁面受次流影响,所以下降的更剧烈;而上壁面处受次流和喷管上壁面固壁的双重挤压,下降得更低。在上游喉道处两者均达到了极值,但下壁面压力高于上壁面压力。气流进入空腔,分离区上部的气流由于流道的扩张,上壁面压力又逐渐升高,在喷管空腔的最大截面处达到最大值;而下壁面因处于回流区,气流压力在空腔扩张段的前段变化小,在空腔中段开始上升。气流进入下游收敛 段出口处,高亚声速主流因受上壁的挤压,近壁气流加速、降压直至出口。而下壁气流受回流区的影响, 气流逆向流动且流速较低,因而壁面静压不降反升。 在临近出口处气流折转加速、降压,流出喷管,下壁面 最高压力位置与上壁面压力相比明显后移。上、下壁 面压力分布差异主要是由于次流的注入使喷管空腔 下部出现了气流分离区,此区域内气流速度较低,速度变化不大,导致空腔下壁面一段压力几乎无变化。而分离区对喷管上壁面的影响相对较弱,因此喷管上壁面静压分布与收缩-扩张喷管的壁面压力分布趋势比较接近。
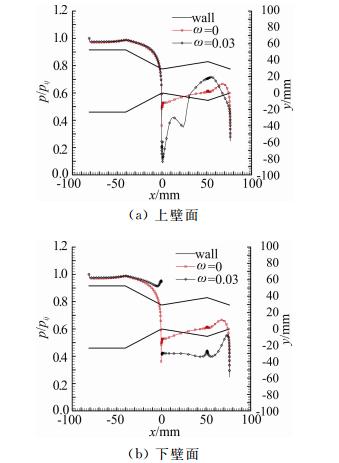 |
| 图 7 DTN上下壁压力分布图(NPR=4,次流流量比3%)Fig. 7 Pressure distributions of DTN up and down walls (NPR=4,secondary flow injection flowrate 3%) |
图 8给出了NPR=2、4、7、10,次流流量比为3%下的DTN特性计算结果。可见,次流流量比3% 下的喷管流量系数(图 8(a))要比无次流情况下(图 4(a))的小约6.5%,比试验结果小约6%。次流对喷 管推力系数影响不大。流量系数在小落压比时增加 较快,随后增速缓慢,原因是随着NPR增加,顺压梯度增大,边界层厚度减小,喉道有效面积有所变大,故 流量系数略有提高,但由于NPR增加,喷管出口欠 膨胀度加大,故推力系数有所减小。图 8(c、d)分别给出了DTN喷管的推力矢量角、推力矢量效率曲 线,由图可见,随着落压比的增加(NPR从2到10), 推力矢量角先减小,随后趋于稳定。原因是在NPR<4 时,DTN尚没有达到完全膨胀,随着喷管总压的增加,气流轴向动量增加,推力矢量角变小;当喷管落压比接近4时,DTN气流已处于完全膨胀状态,上游喉道之后的流动几乎不随NPR变化,因而推力矢量角基本不变;综合来看,NPR在4之后,内流性能的增加有限,为了获得比较好的综合性能,NPR取中间值比较好(典型值在3~4之间)。
 |
| 图 8 不同NPR下DTN内流特性参数对比图 (次流流量比3%)Fig. 8 Internal characteristics of DTN under different NPR (secondary flow injection flowrate 3%) |
图 9给出了DTN喷管流量系数、系统推力系 数、喷管推力矢量角、推力矢量效率数据随次流流量 比变化曲线图。由图可见,数值计算结果与试验结果数据吻合[13]比较好。在NPR=4情况下,随着次流流量比的增加,流量系数逐渐变小,量值从无次流时 的0.926减小到次流流量比6.45%时的0.821;推力 系数也逐渐变小,量值从无次流时的0.965减小到次流流量比6.45%时的0.929。喷管推力矢量角随次流流量比增加,先是增长剧烈,到3%时,推力矢量角达到13.7°,此后随次流流量比继续增大,推力矢量角增速缓慢。推力矢量角增加,主要是因为次流流量增加,相应的次流引射压力增大,使得混合流的横向动量更大,下壁面的分离区也更大,上下壁面压力差增大,从而气流在出口处的偏离角增大。次流的压力增大,使得次流与主流的掺混效应越大,产生更大的推力损失;推力矢量角的增大,使得出口喉道的声速线偏斜更大,因而推力系数随着次流流量比的增加而减小。此外随着次流流量比的增加使得喉道的有效面积减小,故流量系数减小。推力矢量效率随着次流流量比增大而逐渐减小,达到一定值后趋于稳定。
 |
| 图 9 不同次流流量比下DTN内流特性参数对比图(NPR=4)Fig. 9 Internal characteristics of DTN under different secondary flow injectionflowrate (NPR=4) |
通过选定构型和尺寸参数双喉道射流推力矢量喷管(DTN)的数值模拟研究分析,得到以下结论:
(1) NPR在3~4范围时,DTN在无次流情况下具有较高的系统推力系数(可以达到0.968),较小的流量系数(0.93),NPR再增大,系统推力系数迅速下降。为适应更高落压比的工况,应考虑上下游喉道面积比可变的状况。
(2) DTN可以获得比单喉道偏斜矢量喷管更大的推力矢量效率(当落压比为4,次流流量比为3%时,推力矢量效率可以达到4),并且系统推力系数也较高(0.94以上),实现了比较好的综合性能。
(3) 在推力矢量情况下,次流流量比一定时,随着落压比的增加,推力矢量角减小,系统推力系数先增加后减小,流量系数略有增大。
(4) 在推力矢量情况下,落压比一定时,随着次流流量比的增加,推力矢量角增加,而流量系数、推力系数、推力矢量效率减小。
| [1] | Kowal H J. Advances in thrust vectoring and the application of flow-control technology[J]. Canadian Aeronautics and Space Journal, 2002, 48(2):145-151. |
| [2] | Wing D J. Static investigation of two fluidic thrust-vectoring concepts on a two-dimensional convergent-divergent nozzle[R]. NASA TM-4574, December 1994. |
| [3] | Chiarelli C, Johnsen R K, Shieh C F, et al. Fluidic scale model multi-plane thrust vector control test results[R]. AIAA 1993-2433, 1993. |
| [4] | Deere K A. Summary of fluidic thrust vectoring research conducted at NASA Langley research center[R]. AIAA 2003-3800, 2003. |
| [5] | Abdol-Hamid K S, Lakshmanan B, Carlson J R. Application of Navier-Stokes code PAB3D with k-ε turbulence model to attached and separated flows[R]. NASA TP-3480, 1995. |
| [6] | Balakrishnan L, Abdol-Hamid K S. A comparative study of two codes with an improved two-eqtuation turbulence model for predicting jet plumes[R]. AIAA-92-2604, 1992. |
| [7] | Strykowski P J, Krothapalli A, Forliti D J. Cornterflow thrust vectoring of supersonic jets[R]. AIAA-96-0115, 1996. |
| [8] | Flamm J D. Experimental study of a nozzle using fluidic counterflow for thrust vectoring[R]. AIAA -98-3255, 1998. |
| [9] | Hunter C A, Deere K A. Computational inwestigation of fluidic counterflow thrust vectoring[R]. AIAA-99-2669, 1999. |
| [10] | Deere K A, Berrier B L, Flamm J D. Computational study of fluidic thrust vectoring using separation control in a nozzle[R]. AIAA 2003-3803, 2003. |
| [11] | Deere K A, Berrier B L, Flamm J D. A computational study of[LM] a new dual throat fluidic thrust vectoring nozzle concept[R]. AIAA 2005-3502, 2005. |
| [12] | Flamm J D, Deere K A, Mason M L, et al. Experimental study of a dual-throat fluidic thrust-vectoring nozzle concept[R]. AIAA 2005-3503, 2005. |
| [13] | Flamm J D, Deere K A, Mason M L, et al. Design enhancements of the two-dinensional dual throat fluidic thrust vectoring nozzle concept[R]. AIAA 2006-3701, 2006. |
| [14] | Flamm J D, Deere K A, Mason M L, et al. Experimental study of an axisymmetric dual throat fluidic thrust vectoring nozzle for supersonic aircraft applicaiton[R]. AIAA 2007-5085, 2007. |
| [15] | Wing D J. Static investigation of two fluidic thrust-vectoring concepts on a two-dimensional convergent-divergent nozzle[R]. NASA TM-4574, 1994. |
| [16] | Flamm J D. Experimental stusy of a nozzle using fluidic counterflow for thrust vectoring[R]. AIAA-98-3255,1998. |
| [17] | Miller D N, Yagle P J, Hamstra J W. Fluidic throat skewing for thrust vectoring in fixed geometry nozzles[R]. AIAA-99-0365, 1999. |
| [18] | Yagle P J, Miller D N, Ginn K B, et al. Demonstration of fluidic throat skewing for thrust vectoring in structurally fixed nozzles[R]. ASME 2000-GT-0013, 2000. |
| [19] | Luo Jing, Wang Qiang, Eriqitai. Computaitional analysis of two fluidic thrust-vectoring concepts on nozzle flow fleld[J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 30(7):597-601.(in Chinese)罗静, 王强, 额日其太. 两种流体控制方案矢量喷管内流场计算及分析[J]. 北京航空航天大学学报, 2004, 30(7):597-601. |


