0 引 言
钝头体飞行器在超声速或高超声速飞行时，前端将产生强弓形激波，端头表面产生高温高压，形成气动阻力与气动加热。在钝头体前部安装长度合适的杆状减阻杆(又叫激波针)，可以将激波推离物面并形成低压回流区,可以显著的减小钝头体飞行器在超声速飞行时的阻力，在某些马赫数下减阻效率高达50%(相对头部阻力，相对导弹总阻约为10%～20%)[1, 2, 3]。此外，还有研究表明激波针也可以显著降低钝头体表面的热流[4]。然而激波针本身作为驻点所受的气动加热非常强烈，容易被烧蚀，所以需要频繁的更换或者持续降温，这些缺点极大增加了激波针在型号上的应用难度。利用逆向冷喷流将激波推离物面以进行减阻并降低热流的方法，其机理和激波针非常类似，这里利用喷流产生的“空气针”取代了实体的减阻杆。研究表明逆向冷喷流对于减阻和降低表面热流均有良好效果[5, 6],且射流存在两种模态[7]：短穿透到入流模态(Short Penetration Mode，SPM)和长穿透到入流模态(Long Penetration Mode，LPM)，其中只有LPM能够产生显著的减阻效果。然而LPM模态需要较高的喷流压力和喷流流量，长时间使用逆向喷流时就需要配备大量的喷流气体，这就限制了这一技术的应用[8]。为充分发挥激波针和逆向喷流方法各自的优点并克服对应缺陷，有学者提出了将二者结合的带喷流激波针减阻构型[9]，在保持良好的减阻和降热效果前提下，减小了喷流能量需求，而且利用喷流的冷却作用，避免了喷管头部驻点积聚高热流产生的烧蚀问题。
带喷流激波针方法是在钝头体飞行器头部安装一定长度的喷管,飞行器内部气体贮室的气体通过等熵膨胀经喷管射向自由来流,将弓形激波推离物面,并在喷管周围、钝体的前缘形成回流区以达到减阻和降低壁面热流的目的。耿云飞、阎超[9]通过数值模拟的方法研究表明这种方法减阻和降低热流的效果要优于单独采用头部逆向喷流的结果，且适当增大喷管直径,能够加大喷流量进而减弱肩部波系干扰效应,达到减弱局部热流的效果。这种方法更具备工程应用前景，但同时涉及了更复杂的气动现象和参数优化问题，亟需进行优化设计方法研究。
本文利用数值计算获得样本点气动特性，采用IV最优实验设计和响应面方法对激波针外形和喷流压力的耦合效应进行研究，探索一种用于带喷流激波针设计的多参数、多目标优化设计方法。 1 数值方法
采用数 值模拟的方法对超声速条件下带喷流激波针的减阻特性进行了研究。对可压缩N-S方程求解，采用SA一方程湍流模型。来流入口采用远场边界条件，出口采用压力出口边界条件，物面采用等温壁、无滑移边界条件。喷流入口采用总压与总温恒定的压力入口边界条件。来流马赫数Ma∞=2.5，总温T0=487.4625K，总压p0=268358.3Pa，喷流出口Maj=2.5。文中激波针长度和喷流直径均用头部半径进行无量化表示，即Lj/R和Dj/R(R=75mm)，喷流出口总压用来流波后总压进行无量纲化表示，即p0j/p02。 2 响应面优化方法
响应面法( Response Surface Methodology，RSM) 是数学方法和统计方法结合的产物[10]，是用来对所感兴趣的响应受多个变量影响的问题进行建模和分析,其最终目的是优化该响应值。响应面法和其他一些直接优化方法相比有如下的优点[11, 12, 13]: (1) 响应面法能消除目标函数的高频噪声，因此可期望得到全局的近似最优解； (2) 在优化设计过程中针对不同的目标函数和约束条件，不需要增加额外的计算量；(3) 响应面法能较容易地应用于多学科、多目标、多约束的优化设计问题中； (4) 采用响应面法进行优化设计时不需要修改流场分析程序，更容易在设计部门推广。因而该方法具有高效、实用的特点，在复杂非线性优化问题中有较好的应用前景。
响应面法是一种实验条件寻优的方法，囊括了实验设计、建模、响应面模型检验、寻求最佳组合条件等众多实验和统计技术。通过对过程的回归拟合和响应曲面、等高线的绘制、可方便地求出相应于各因素水平的响应值。在各因素水平的响应值的基础上，可以找出预测的响应最优值以及相应的实验条件。带喷流激波针响应面法优化流程如图 1所示，最终不仅获得最优参数条件，还能够得到各参数对减阻特性的影响规律。
 |
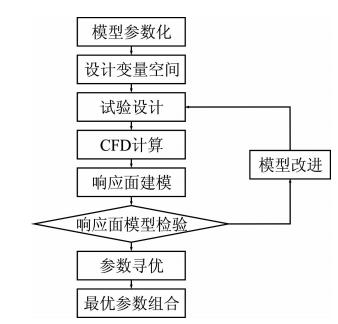| 图 1 带喷流激波针参数响应面法优化流程图Fig. 1 Flowchart of optimization of the combination of spike and forward-facing jet using response surface methodology |
本文优化目标是最佳减阻效果和最少喷流流量。工程设计中的优化自变量较多，包括激波针的长度、 直径、头部形状、喷流总压、喷流马赫数、喷流出口直径和形状等，综合其主次关系，本文优化变量为激波针长度、喷流出口总压和喷流出口直径这三个主要参数。钝头体为球柱体外形，头部为半径R=75mm， 圆柱段直径为D=150mm，钝头体总长为L= 225mm，激波针长度和喷流出口直径分别用Lj和Dj表示。根据前期对基本特性的研究，给定了优化设计的空间：
杆长Lj/R： 0~4；
直径Dj/R： 0.06~0.2；
喷流总压p0j/p02： 1~31。
带喷流激波针构型优化设计的目标是最佳的减阻效果和最少的喷流气源携带量。减阻效果通过新外形阻力和钝头体阻力的比值表示，同时扣除了喷流本身产生的反推力。喷流气源携带量用所需喷流的质量流量表示。二者的优化目标均为最小化，采用期望函数法进行多目标寻优，期望函数可表示为：
其中，r1、r2为权重，在1-5之间取值，d1、d2为阻力和流量的期望评估值，通过下式得到：
响应面模型的一般形式为：
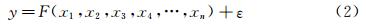
考虑到带喷流激波针构型气动特性的非线性显著，采用三次多项式构建响应面模型。如果进行ns次实验，响应值可以表达为：
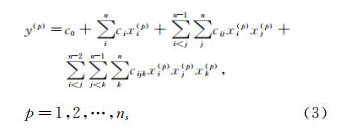
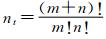个。通过最小二乘法得到回归系数就可建立响应面模型。响应面生成后，为了保证模型的适应性，还需要进行预测能力评估，通常采用R2(复相关系数)、Ra2(修正的复相关系数)和%RMSE(均方根误差)的值预测能力的评估，计算公式为：
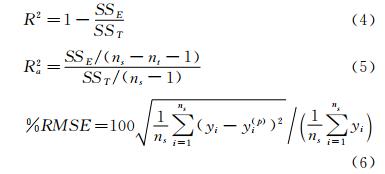
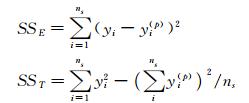
本文采用的 是3元3阶多项式响应面模型，待定回归系数为20个。尽管进行20次不同自变量取值的实验就可以满足响应面模型的确定，但要保证响应面模型的具备足够小的预测不确定度，还需要更多测量点。采用假设检验方法分析其回归显著性，可知要使得响应面预测值具备平均95%置信概率能够不会与设计空间中任一点的实验结果出 现显著差异，实验样本点数量ns和回归系数个数nt之间有以下关系[14]：
所以，对于本实验样本点只要达到33个(ns=1.625×20=32.5)就可以满足航空航天工程应用中通常能够接受的95%置信度约定。
确定了设计空间内实验样本点的数量后，需要进行适当的样本点取值设计，使拟合出的响应面模型在未知点有较强的预测准确性，这也就是实验设计[15, 16]问题。考虑到响应面建模存在着一些对模型建立影响非常大的位置，这些位置的点会有杠杆效应，其误差会在整个模型中被放大，所以增加了一定量的重复点以消除杠杆效应，同时重复点也可以用于对数值计算精度的评估。本文采用了Ⅳ-最优化方法，这种方法是寻求设计空间的整体预测方差最小的设计，非常适合于精度要求较高的响应面模型的建立。 实验设计结果共有33个组合状态，如图 2所示。其中包括8个重复状态，在计算时通过改变网格结构和点数实现。
 |
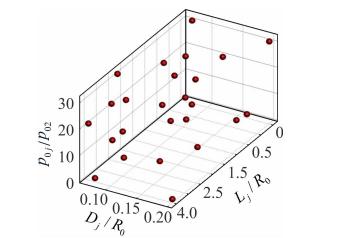| 图 2 数值计算设计点空间分布图Fig. 2 Distribution of the design points for numerical calculation |
对设计点进行CFD流场计算后，可以建立自变量为杆长Lj/R、直径Dj/R和喷流总压p0j/p02，响应变量为设计点外形与单独钝头体的阻力比的响应面模型。在回归过程中对多项式各项进行显著性检验，剔除了影响不显著的项，表 1给出了响应面模型各项系数值。表 2给出了响应面模型的拟合度量值，一般要求R2和Ra2的值在0.9以上，可以看出响应面模型对气动力规律的拟合是有意义的，可以用来规律研究和优化设计。
| 项 | 系数 | 项 | 系数 |
| 截距 | 1.083361 | p0j/p202 | 0.001285 |
| Lj/R | -0.39721 | Lj/R×Dj/R×p0j/p02 | 0.022359 |
| Dj/R | -0.61149 | Lj/R2×p0j/p02 | -0.00114 |
| p0j/p02 | -0.02114 | Lj/R×p0j/p202 | -0.00014 |
| Lj/R×Dj/R | -0.04409 | Dj/R2×p0j/p02 | 0.587027 |
| Lj/R×p0j/p02 | 0.009081 | Dj/R×p0j/p202 | 0.004317 |
| Dj/R×p0j/p02 | -0.30685 | Lj/R3 | -0.01104 |
| Lj/R2 | 0.114868 | p0j/p302 | -2.3×10-5 |
| Dj/R2 | 1.491256 |
| 评价指标 | R2 | Ra2 | %RMSE |
| 评估值 | 0.9646 | 0.9533 | 4.6 |
为了认识激波针长度、喷流出口总压和喷流出口直径对流场特性的影响和机理，首先从单因素的角度对其进行分析。选取了6个典型状态进行流场计算和分析，状态参数和计算结果见表 3，其中状态0为作为参考的单独钝头体。图 3给出了这几种组合的头部表面压力分布比较。
| 状态 | Lj/R | p0j/p02 | Dj/R | 阻力比 | 流量/(kg·s-1) |
| 0 | 0 | — | — | 1 | 0 |
| 1 | 0.5 | 7 | 0.1 | 0.635 | 0.0287 |
| 2 | 2 | 7 | 0.1 | 0.454 | 0.0287 |
| 3 | 0.5 | 14 | 0.1 | 0.551 | 0.0574 |
| 4 | 0.5 | 7 | 0.06 | 0.638 | 0.0103 |
| 5 | 0.5 | 7 | 0.13 | 0.554 | 0.0485 |
 |
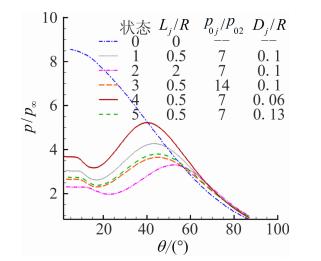| 图 3 典型组合状态的头部表面压力分布比较Fig. 3 Comparison of surface pressure distributions on the noses of the typical configurations |
(1) 不同激波针长度流场。状态1和状态2分别是激波针杆长与头部半径之比为Lj/R为0.5和2的外形，可以看出两种采用带喷流激波针钝头体表面压力分布显著低于单独钝头体的，长杆的钝头体表面压力要低于短杆的。这是由于在相同的喷流条件下，增加杆长可以增加头部脱体激波的距离，降低头部压力值。带喷流激波针钝头体的阻力与单独钝头体之比，在杆长Lj/R=0.5和2的条件下分别为0.635和0.454，长杆的阻力要比短杆的小28.5%，说明杆长对减阻效果影响明显，在这两个算例的条件下，杆长越长减阻效果越好。
图 4给出了状态1和状态2的流场 等压力线分布和头部流线分布的对比。可以看出由于杆长的作用，长杆流场的主激波脱体距离比短杆的增大很多，由于长杆的喷流出口前伸，单独喷流对主激波的前推的能力减小，这和文献[9]的研究结果一致。长杆外形在激波针所处位置产生的回流区要显著大于短杆外形的，产生的涡强度也更大。这使得长杆外形在三个方面起到更好的减阻效果：1)回流涡对钝头体的影响区域增加；2)回流涡强度更大，使得钝头体表面压强更小；3)长杆回流区呈现扁平结构，对主流整流效果更显著，减小 再附点压力突增。杆长增加对减阻有利，但在应用上也增大了激波针结构稳定性和储藏的难度。
 |
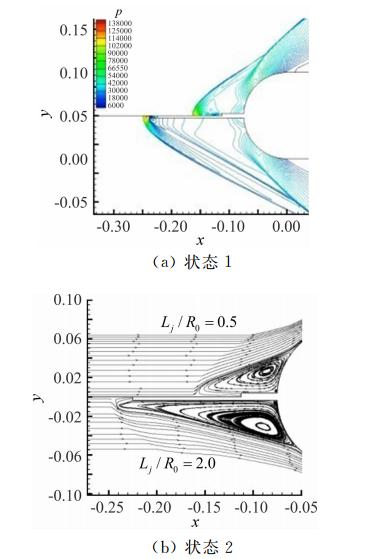| 图 4 两种带喷流激波针外形的流场等压力线分布和流场流线比较Fig. 4 Comparison of Pressure contours and streamlines between two configurations with the combination of spike and forward-facing jet |
(2) 不同喷流总压流场。状态2和3的喷流出口总压与来流波后总压之比p0j/p02分别为7和14，可以看出由于总压大的喷流具有更大的能量，可以将头部脱体激波推出更远，进一步降低了头部压强。p0j/p02为7和14的钝头体外形阻力和单独钝头体外形阻力之比分别为0.635和0.551，高喷流总压的阻力要比低喷流总压的小13.2%，所以增加喷流总压可以减小钝头体阻力。分析状态2和3的流场，主激波前推距离由50 mm增加到了65.8 mm(从喷流出口到主激波算起)，前推距离增加了30.9%。增大喷流总压增加了回流涡的体积和强度，但质量流量更大，需要携带更多的喷流气源，设计时需要综合考虑。
(3) 不同喷流出口直径流场。状态4和5的喷流出口直径与头部半径之比Dj/R分别为0.06和0.13。由图 3可以看出，喷流直径增大有利于降低头部压强，Dj/R为0.06和0.13的阻力比分别为0.638和0.554，后者阻力比前者小了15.2%，所以增加直径比可以进一步减小钝头体阻力。通过比较状态4和5流场发现直径增加了一倍多，主激波前推距离由34 mm增加到了64 mm(从喷流出口到主激波算起)，前推距离增加了88.2%。增大直径使回流涡的强度和影响区域变大，但也要增大喷流质量流量。 3.2.2 多因素耦合气动规律
由于本文建立响应面模型的形式是设计参数为自变量的多项式，其各项系数有显著的物理意义。通过表 1可看出钝头体阻力与激波针长度、喷流直径及喷流总压呈不同程度的非线性关系，而且耦合作用非常明显。Lj/R和阻力比呈3阶关系，Dj/R和p0j/p02和阻力比呈2阶关系。Dj/R的耦合作用最强，尤其是与p0j/p02的1阶和2阶交叉项系数较大。响应面模型给出了阻力与各参数的函数关系，可以得到设计空间内任意组合的阻力预测值及其95%置信概率区间，能够满足飞行器设计的要求。
由于气动规律的非线性耦合，绘制响应面图更有助于研究气动规律。图 5给出了带喷流激波针减阻效果随三个参数Lj/R、p0j/p02和Dj/R的响应面图。垂直坐标和响应面颜色都代表带喷流激波针钝头体阻力与单独钝头体阻力的比值。可以看出在没有喷流(p0j/p02=1)和喷流压力较小时，钝头体阻力随激波针长度增加先快速减小，在Lj/R大于2之后，减小的幅度就不大了。随着喷流压力的增加，喷流对减阻的贡献逐渐显著，阻力减小随激波针长度变化逐渐平缓。当喷流直径比较大的时候，继续喷流压力和激波针长度对减阻效果影响很小，阻力甚至会有所上升。经过流场分析发现当头部激波被推离钝头体远到一定程度，钝头体表面压力分布随激波针和喷流参数的变化不再明显，而喷流反推力导致阻力显著增大，最终产生此现象。
随着喷流总压增大总体上能够使阻力减小，但显然这个效果和激波针的长度和喷流直径是相关的。在激波针长度较短的条件下，喷流直径的增大能够明显增加阻力随喷流总压增加减小的速度。而在激波针Lj/R近似大于2之后，喷流总压增加对阻力减小的作用不再明显，在喷流Dj/R＞0.18之后，阻力还有增加的趋势，这也是由于喷流反推力的作用。
随着喷流直径的增大，在Lj/R和p0j/p02不大时阻力减小。与激波针长度和喷流总压的影响相比，喷流直径的影响较小。从图 5中阻力比的颜色可以看出，设计空间内最小的阻力比出现在Dj/R=0.14~0.20的范围内。
图 5的响应曲面非常直观的给出了阻力比随设计参数变化的规律，从总体规律上看，钝头体阻力随Lj/R和p0j/p02变化明显，先随着二者增大迅速减小，之后阻力变化逐渐平缓或增加，在Dj/R=0.10~0.20范围内呈现出凹曲面规律，存在极小值点，最小阻力比为36%。
 |
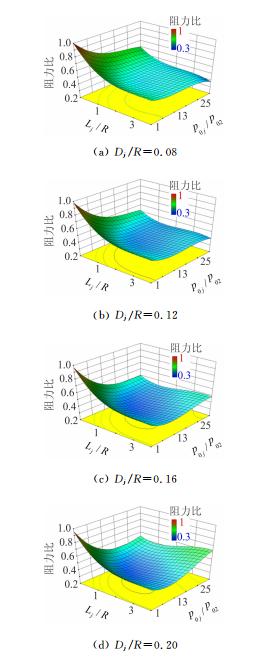| 图 5 带喷流激波针减阻效果随Lj/R、p0j/p02 和Dj/R变化的响应面Fig. 5 Response surfaces of drag-reducing effects along with Lj/R、p0j/p02 and Dj/R of spike and forward-facing jet |
3.3 优化结果
优化目标是最小阻力比和喷流质量流量，喷流质量流量可以根据喷流气流参数和喷流直径计算得到，与p0j/p02和Dj/R的关系如图 6所示。
 |
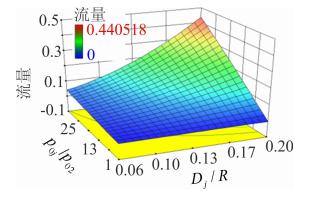| 图 6 喷流质量流量与p0j/p02和Dj/R的关系Fig. 6 Relationship between mass flow of injection and p0j/p02 & Dj/R |
飞行器设计中激波针杆长与伸缩机构能力和结构稳定性有关，所以分为4个杆长区间进行寻优，表 3给出四个杆长区间最优结果。可以看出期望值最高的为0.95171，其阻力比为0.408，减阻效果达到59.2%。如果考虑到激波针结构稳定性问题，可以选择Lj/R=2.36的杆长，期望值为0.93223，减阻效果57.1%，所需要的流量为0.044kg/s。在利用响应面模型优化完成后，对优化后的组合流场进行CFD计算验证，第二个外形计算所得阻力比是0.43561，与预测值相差1.5%，说明响应面法预测的精度比较高。普通导弹每秒燃料消耗的质量为在公斤量级，即使对由于实际飞行器尺寸导致的流量增量，喷流质量流量也相对是小量，所以带喷流激波针减阻效果和付出的代价相比是非常理想的。
本文对钝头体带喷流激波针减阻特性的气动特性进行研究，将实验设计、响应面优化法和数值计算结合，分析了带喷流激波针气动规律，探索了以减阻效果和喷流流量为目标的多参数、多目标优化设计方法，主要结论有：
(1) 响应面模型给出了阻力与各参数的函数关系，可以的到设计空间内任意组合的阻力预测值及其95%置信概率区间。
(2) 激波针长度、喷流总压和喷流出口直径对与阻力的呈现2阶或3阶非线性关系，且相互耦合，其中Dj/R的耦合作用最强，尤其是与p0j/p02交叉效应明显，存在极小值点，最大减阻64%。
(3) 获得了最小阻力和喷流质量流量的最优参数，减阻57.1%，流量为0.044 kg/s。
研究表明用响应面法进行参数优化设计，有计算量小、结果可信、实用性强的特点，在飞行器设计中有很好应用前景。
| [1] | Hutt G R, Howe A J. Forward facing spike effects on bodies of different cross section in supersonic flow[J]. Aeronautical Journal, 1989, 93(926):229-234. |
| [2] | Feng Jiabo, Zhang Jiang. Drag reduction for the forward-facing spike on the blunt nosed researching via CFD and wind tunnel experiments[C]//Fourth session of the national hypersonic aerodynamics/heat Symposium Proceedings. Wenzhou, 2007:10-13. (in Chinese)冯家波, 张江. 钝头体激波针减阻数值计算与风洞实验研究[C]//十四届全国高超声速气动力/热学术交流会论文集, 温州, 2007:10-13. |
| [3] | Jiang Wei, Yang Yunjun, Chen Hewu. Investigations on aerodynamics of the spike-tipped hypersonic vehicles[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(6):28-32.(in Chinese)姜维, 杨云军, 陈河梧. 带减阻杆高超声速飞行器外形气动特性研究[J]. 实验流体力学, 2011, 25(6):28-32. |
| [4] | Yamauchi M, Fujii K, Higashino F. Numerical investigation of supersonic flows around a spiked blunt body[J]. Journal of Spacecraft and Rockets, 1995, 32(1):32-42. |
| [5] | Meyer B, Nelson H F, Riggins D W. Hypersonic drag and heat-transfer reduction using a forward-facing jet[J]. Journal of Aircraft, 2001, 38(4):680-686. |
| [6] | Finley P J. The flow of a jet from a body opposing a supersonic free stream[J]. Journal of Fluid Mechanics, 1966, 26(02):337-368. |
| [7] | Fomin V M, Maslov A A, Malmuth N D, et al. Influence of a counterflow plasma jet on supersonic blunt-body pressures[J]. AIAA Journal, 2002, 40(6):1170-1177. |
| [8] | Josyula E, Pinney M, Blake W B. Applications of a counterflow drag reduction technique in high-speed systems[J]. Journal of Spacecraft and Rockets, 2002, 39(4):605-614. |
| [9] | Geng Yunfei, Yan Chao. Numerical investigation on drag and heat-transfer reduction using combined spike and forward facing jet method[J]. Acta Aerodynamica Sinica, 2010, 28(4):436-440.(in Chinese)耿云飞, 阎超. 联合激波针一逆向喷流方法的新概念研究[J]. 空气动力学学报, 2010, 28(4):436-440. |
| [10] | Wang Yongfei, Wang Chengguo. The application of response surface methodology[J]. Jounnal of CUN. Natural Sciences Edition, 2005, 14(3):236-240.(in Chinese)王永菲, 王成国. 响应面法的理论与应用[J]. 中央民族大学学报:自然科学版, 2005, 14(3):236-240. |
| [11] | He Wei, Xue Weidong, Tang Bin. Optimization of experimental design and data analysis methods[M]. Chemical Industry Press, 2011.(in Chinese)何为, 薛卫东, 唐斌. 优化试验设计方法及数据分析[M]. 化学工业出版社, 2011. |
| [12] | Xiong Juntao, Qiao Zhide. Optimum aerodynamic design of tran sonic wing based on response surface methodology[J]. Journal of Experiments in Fluid Mechanics, 2005, 19(1):104-108.(in Chinese)熊俊涛, 乔志德. 基于响应面法的跨声速翼型气动优化设计[J]. 实验流体力学, 2005, 19(1):104-108. |
| [13] | Box G E P, Draper N R. Response surfaces, mixtures, and ridge analyses[M]. New York:John Wiley & Sons, 2007. |
| [14] | DeLoach R, Micol J R. Comparison of resource requirements for a wind tunnel test designed with conventional vs. modern design of experiments methods[R]. AIAA 2011-1260. |
| [15] | Fisher R A. The design of experiments[M]. 1st ed., Edinburgh:Oliver and Boyd, 1935. |
| [16] | Montgomery D C, Montgomery D C. Design and analysis of experiments[M]. New York:Wiley, 1997. |