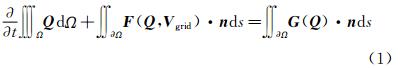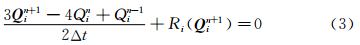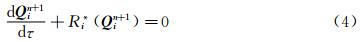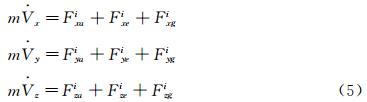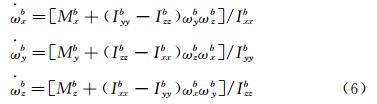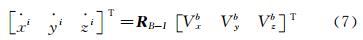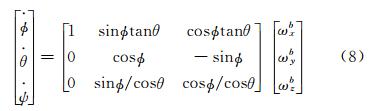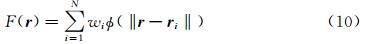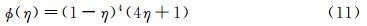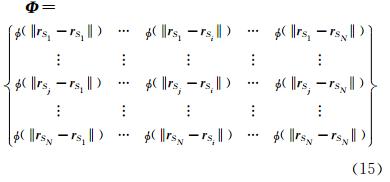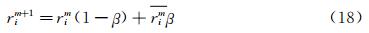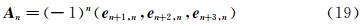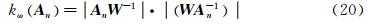0 引 言
多体分离是实际飞行器设计中需要经常面对的技术问题。常见多体分离问题包括外挂物与载机分离过程、座舱盖/座椅的弹射过程、多级火箭的级间分离、多弹头再入时的展开、子母弹抛撒过程等。此类问题包含的分离体数目多、相对位移大、气动力非定常效应显著、气动干扰严重[1]。目前，多体分离轨迹问题主要依托风洞实验和数值模拟两类考察手段。风洞实验采用的技术方法主要有捕获轨迹系统(CTS)，自由投放方法(又称动态投放实验)，网格扫描方法和流向角方法等。总体来说，地面设备不足使得采用风洞实验手段研究多体分离问题相对比较困难，尤其是在高速机动飞行等非常规情况下，实验研究的局限性愈发明显。自由投放实验费用高，危险性强，而且不易测量。CTS往往费用高昂，实验状态极多[2]。近年来，数值方法的进步使得仿真计算越来越能逼近现实状况，采用数值方法模拟多体分离轨迹也逐渐成为一种常用的技术手段。在CFD工作者的不懈努力下，多体分离问题的数值模拟方法已经从最初的准定常计算发展为完全非定常模拟[3]。采用非定常数值方法进行多体分离轨迹仿真时必须解决的核心问题是：如何采用动态计算网格刻画各固壁边界之间幅度很大的相对运动。针对这一问题，国内外采用的动态网格技术大致分为以下几类：
第一类是嵌套网格技术，这类技术已经发展的比较成熟，是一种国内外很常用的求解多体分离问题的方法。但嵌套网格由于运动子块之间及其与背景网格之间的相对位置随时间变化，所以交叠区内的人工边界即所谓“洞”边界必须每个时间步都重新建立，重新定义计算网格。在计算中需要在重叠区频繁地进行插值运算，实现运动子块的物理量传递，这会带来解的精度损失[4]。
第二类是网格变形方法，这类方法在非结构网格中运用较多，代表性算法包括弹簧法、弹性体方法、Delaunay图法和径向基函数网格变形方法等。弹簧法需要构建和求解大型矩阵，计算量大，而且主要是针对四面体非结构网格。弹性体方法对任意网格类型都适用，并能很好地保证变形后的网格质量，但其计算量非常大，难以在非定常流动计算中多次反复使用。Delaunay图法具有较高的效率和鲁棒性，但难以处理较大变形。近年来，采用径向基函数(RBF)插值的网格变形方法逐渐兴起。该方法先运用径向基函数对物面边界网格节点的位移进行插值，再利用构造出来的径向基函数序列将物面的位移效应光滑地分散到整个网格区域的节点上[5]。结合数据精简算法的RBF网格变形技术在处理小幅变形问题时具有很高的效率，且网格质量可以得到保证。但是，单纯的RBF网格变形技术存在极值聚集现象，对于多体分离问题中的超大幅度网格变形，在极值的积累效应下，计算网格易被破坏。
第三类是计算网格重新生成技术。对于结构化网格，由于其拓扑结构相对固定，因此可以在计算过程中根据边界位置运用代数方法重新生成新的网格。而非结构网格下的网格局部重生办法则要复杂得多。由于每一次网格重生都可能会改变原先的网格节点和网格单元的对应关系，这给流场信息的传递带来了不便。对于非结构网格下的大幅度变形问题，人们往往采用网格变形和网格局部重生相结合的策略。在单步小位移的情况下利用弹簧法或RBF方法进行网格变形，当总位移逐渐增大至网格质量低于设定标准时，进行局部网格重新生成[6, 7]。这种方法能够保证整个分离过程中的网格质量，但网格重生过程影响效率，且在物理信息传递中会产生插值精度损失。
为了克服多体分离大变形中网格质量易下降、流场信息插值精度易损失的问题，本文发展了一套RBF和改进的拉普拉斯光顺相结合的网格变形技术。采用整体网格，在单步小幅变形时选用RBF方法实现网格变形，当网格质量下降到设定标准以下时引入改进的拉普拉斯光顺，在不破坏网格节点之间相邻关系的前提下进行网格节点的局部光顺调整，使网格质量得到改善。本文将这一网格变形方法应用于多体分离问题的数值模拟，耦合求解非定常NS方程和六自由度运动方程，形成了一套基于动态混合网格的多体分离问题数值模拟方法。利用该方法数值模拟了典型的多体分离标模问题(机翼 /外挂物分离)，并与AEDC风洞实验结果[8]进行了对比。 1 理论背景 1.1 非定常N-S方程求解
本文使用的流场求解器是作者课题组自主开发的一套基于非结构混合网格的雷诺平均N-S方程求解程序，简称HUNS3D[9]。为了考虑固体边界的六自由度运动，流动控制方程采用ALE(Arbitrary Lagrangeian Eulerian) 方法描述的非定常雷诺平均N-S方程。在计算网格的任意运动和变形情形下，该方程在直角坐标系下的积分形式为:
式中， Q 为守恒变量，Q = ρ,ρu,ρv,ρw,ρE T，Ω为控制体，Ω表示控制体单元边界，V grid为网格运动速度，n 为控制体单元边界外法线方向向量，F(Q)、G(Q) 表示N-S方程的无粘通量项和粘性通量项，方程(1)经过格心有限体积法空间离散后，可以得到在网格单元i上的半离散形式： 其中：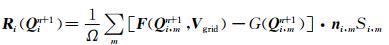
式中，R为残差，m为网格单元i的面元标号，S为对应的网格面元面积。
隐式时间格式下，对于方程(2)的时间导数项采用二阶向后差分离散可得：
其中，Δt代表时间步长，上标n代表真实时间迭代的步数。
方程(3)的直接求解比较困难，可以采用双时间迭代技术进行求解。通过在方程(3)的左端加入守恒变量对虚时间的导数项得：
其中，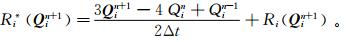
运用求解定常流动的时间推进算法对方程(4)进行虚时间迭代求解，当迭代达到收敛标准，即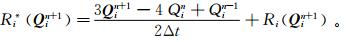时，相应地有Ri*(Qi(k+1))≈0。显然，此时的Q(k+1)可以被视为方程(3)的近似解，也就是真实时间层第n+1时间步的流动参数值 Q n+1。具体方法可参见文献[10, 11]。
1.2 六自由度运动方程求解
多体分离问题中，被考察的物体一般有六个自由度。相应的有六个动力学方程，其中三个描述平动，三个描述转动。另外，还有六个相对应的运动学方程，分别确定物体的空间位置和姿态[12]。考虑图 1中给定的地面坐标系[13]，X轴平行于地平面指向某任意选定方向，Z轴铅垂向下，Y轴垂直XZ平面，按右手定则确定方向。地面坐标系与固连于飞行器并随飞行器运动的随体坐标系之间的夹角构成了飞行器的姿态角。随体坐标系中X轴在飞行器对称平面内，平行于机身轴线指向前；Z轴亦在对称平面内，垂直于X轴；Y轴垂直对称平面指向右。在图 1中，φ为滚转角，θ为俯仰角，ψ为偏航角。
 |
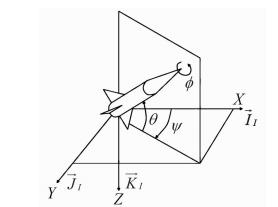| 图 1 外挂物欧拉角示意图Fig. 1 Eular angles of store |
(1) 图 1所示的参考系中，六个动力学方程描述为：
惯性系下的质心平动方程
体轴系下的绕质心转动方程：
(2) 六个运动学方程包括：
描述质心空间位置变化的运动方程:
描述刚体空间姿态变化的运动方程:
公式(5)~(8)中，m代表质量，V为速度，F为力，ω为角速度，M为外力矩，I为惯性矩；上标i和b分别表示惯性坐标系和体轴系；下标a、e、g分别代表气动力，外力(发动机推力)，体积力。 R B－I为体轴系到惯性系转换矩阵,详细表达式参见文献[12]。
刚体运动方程的求解属于常微分方程初值问题，令 l =[Vx,Vy,Vz,ωx,ωy,ωz,x,y,z,θ,ψ,φ]，则刚 体运动方程可以写为:
本文采用改进的Adams预估校正法[14]求解刚体运动方程。 1.3 径向基函数(RBF)网格变形技术
径向基函数插值的一般形式是:
这里的F( r )是插值函数，N代表插值问题所使用的径向基函数的总数目，φ(‖ r － r i‖)是所采用的径向基函数的通用形式，‖ r － r i‖是位置矢量 r 到 r i的距离，r i代表第i号径向基函数的支撑点的位置，wi是与第i号径向基函数相对应的权重系数。径向基函数的类型很多，本文选取的是比较适合网格变形插值使用的Wendland C2函数，其具体形式如下：
这里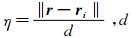
为径向基函数的作用半径，当η>1时，强制设定φ(η)的值为0。在网格变形时用径向基函数插值进行近似描述的不是物面网格节点的实际位置，而是网格节点的变形位移分布。为了叙述方便，将上述径向基函数插值问题的插值条件用以下矩阵形式描述:
这里下标S表示物面属性，Δ X S= {ΔxS1,…,ΔxSN} T、Δ Y S= {ΔyS1,…,ΔySN} T和Δ Z S= {ΔzS1,…,ΔzSN}T分别表示N个物面边界节点在x、y、z方向上的位移分量； W X= {wS1x,…,wSNx} T、 W Y= {wS1y,…,wSNy} T和 W Z= {wS1z,…,wSNz }T是待定的权重系数序列；矩阵 Φ 的具体形式为：
通过方程(12-14)求解出 W X、 W Y和 W Z后就可以获得物面位移的径向基函数插值。这样计算域内任意网格节点j的位移就可以通过公式(10)确定。
上述径向基函数网格变形方法的关键环节是将物面变形位移通过径向基函数插值来近似代替的过程，也就是建立和求解方程(12)~(14)的过程。为了叙述方便，以下将方程(12-14)描述的插值条件统一表述为下面的形式:
为了提高网格变形效率，采用文献[5]的改进的贪心算法在物面节点位移的拟合过程中进行数据精简，在满足网格变形精度要求的前提下，可以尽量降低条件矩阵 Φ 的维数。 1.4 一种改进的拉普拉斯光顺和网格质量评估函数
径向基函数网格变形算法虽然具有良好的鲁棒性和 很高的计算效率，但是在单独使用它处理多体分离带来的超大幅度网格变形时局部网格质量会下降，严重时甚至导致网格拓扑破坏。所以当局部网格单元质量下降到一定程度时，需要运用网格光顺，改善变形后的网格质量。经典拉普拉斯光顺的原理是：调整每个网格顶点至其相邻顶点的几何中心。本文对其进行改进[15]，移动顶点时考虑网格质量，仅当该顶点连接的网格单元质量获得有效提高时，才对该顶点进行移动。
当确定光顺区域后，节点新的位置按如下方法计算：
其中，rmi 是与节点i相邻的所有节点的几何中心矢量坐标，rmj是节点i的相邻节点矢量坐标，ni是节点i的相邻节点个数。eij是节点i与相邻节点所成边的长度。节点i的新位置可以通过下式计算： 其中，β为初始松弛因子，一般取0.5左右。
本文中拉普拉斯光顺启动的判据是：调整节点后，与该节点相邻的所有网格单元的最差质量系数被提高且平均质量系数保持在原来80%以上。对于非结构混合网格，通常有四面体、金字塔、三棱柱、六面体四种网格单元类型。针对上述这四种网格单元，本文提出一套统一的网格质量评估函数。下面简要介绍这种网格质量评估函数。
对于四面体单元，令T作为任意一个包含四个节点的四面体单元，节点用Pn表示，n=0,1,2,3。定义边矢量 e k,n=xk－xn(k≠n ,k=0,1,2,3)，节点n处的四面体单元雅克比矩阵为:
令αn代表 A n的行列式。四面体体积V(T)=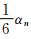
，所以，A n的构成应使αn>0。
定义正四面体 T e，其四个顶点坐标为(0,0,0),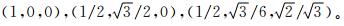
让 W n代表 T e第n个顶点的雅克比矩阵。如:
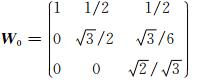
令T+代表任意具有正体积的四面体，其雅克比矩阵 A n可逆，定义雅克比矩阵 A n的加权条件数为:
其 中 W=W 0。令Sn=AnW－1，Sn实际反映的是由正四面体向所求四面体转换的线性关系。kω( A n)即线性转换矩阵Sn的条件数。据此，定义网格质量评估函数为:
具体推导过程可参见文献[16]。该函数具有优良网格质量评估函数所应具备的五大特点，分别是：
① 它是关于节点坐标的连续函数。
② 网格单元刚性旋转其函数值不变。
③ 函数取值范围在0到1之间，取值越大代表网格质量越好。
④ 正四面体刚性放大或旋转时其函数值始终为1。
⑤ 对于一个质量较好的网格，等比例缩小使其体积趋近于0，其值不变。只有当网格体积趋近于0且存在某相邻棱边的长度不相应趋近于0时其函数值才趋近于0。
本文将该函数扩展应用到金字塔、三棱柱和六面体三种网格单元类型中。把单元每个顶点及与其相连的三边视作一个四面体，分别写出各自的雅克比矩阵，求解各自的质量系数，即3/kω函数值，所有顶点的函数值的平均值即为该类型网格单元的质量系数，此时的理想四面体雅克比矩阵 W 应根据具体网格类型下具体顶点处理想的四面体形式相应给出。例如，六面体下任一顶点的理想四面体是：与顶点相邻的三条棱边为单位长度且互相垂直的四面体。对于金字塔单元，有一个顶点与四条边相邻，不能够给出该顶点处的三阶雅克比矩阵。此时应将其由对角线剖开成两个四面体，分别计算这两个四面体的质量系数，再取平均值，该值即为该顶点在金字塔网格单元中的 质量系数。如图 2，对于顶点5，其质量系数为顶点 5、1、4、2和顶点5、3、2、4所构成的两个四面体质量系数的平均值。
 |
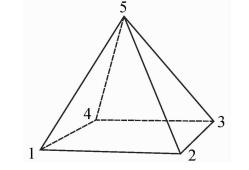| 图 2 金字塔单元点序示意图Fig. 2 Node list of pyramid unit |
理论和实践均证明，上述网格质量评估函数可以对四种网格的网格单元的质量进行统一的刻画，且具有良好的取值特性。 2 算例验证 2.1 模型几何参数
选择AEDC外挂物投放标模作为算例考察本文方法在多体分离问题中的鲁棒性和精度。AEDC模型有较详细的几何数据和实验数据[8]，很多研究者都选用它做多体分离问题的研究算例[17, 18]。AEDC模型的机翼为一个具有45°倾斜角的三角翼，机翼展向截面为NACA-64A010翼型。挂架的构造为一个对称的弧面-平面-弧面组合体，对称线沿展向距翼根弦线的距离为3.3m，挂架顶点距机翼前缘的距离为0.61m。外挂物为带有四个对称尾翼的旋成体，其中心圆柱体直径为0.5m，总长度为3.017m。外挂物和挂架之间的距离只有3.66cm。外挂物质心前后作用两个弹射力分别为10.7kN和42.7kN，作用时间0.054s。其他具体参数见图 3和文献[17]。
 |
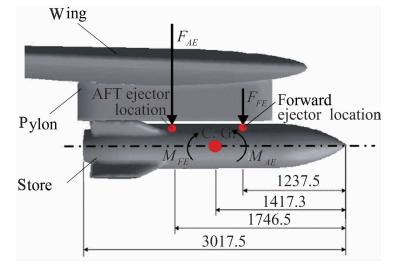| 图 3 机翼外挂物模型几何参数示意图(mm)Fig. 3 Geometry parameters of wing-store model(mm) |
由于外挂物和挂架之间的距离太小，一般的网格生成软件没有办法在附面层内生成粘性网格。本文采用的方法是将机翼和外挂物拉开一段距离生成附面层内的粘性网格后，再采用RBF网格变形技术将机翼外挂物还原至它们的初始位置。模型表面网格点数为53 135，表面单元数为75 992。整体网格共有 1 531 886个节点和3 275 111个单元。表面网格及挂架外挂物之间的空间网格如图 4所示。来流马赫数为0.95，单位雷诺数为7.874×106，攻角0°，飞行高度是8000m。流场求解采用Roe格式进行有限体积的空间离散，双时间方法进行时间推进，隐式LU-SGS格式进行虚时间层迭代，湍流模型采用Menter的k-ω SST两方程模型。RBF网格变形的收敛标准为1×10-5，采用精简算法时，径向基函数的支撑点的个数限制在1500内。若在网格变形过程中选择1500个点还未降到收敛标准以下，不再继续加入更多的支撑点。
 |
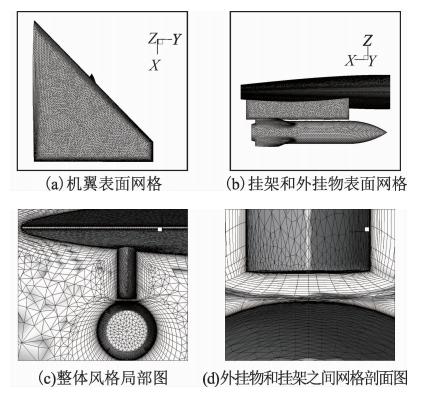| 图 4 表面网格和初始网格示意图Fig. 4 Surface mesh and initial volume mesh |
初始时刻定常流场计算的压力分布如图 5所示。由于流动是跨声速的，因此在外挂物中部和尾部区域出现激波。由于吊舱和挂架很近，二者之间有较强的气动干扰，使这一块区域的流动比较复杂。
 |
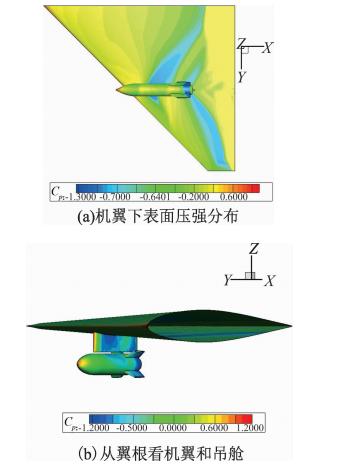| 图 5 初始时刻压强分布云图Fig. 5 Pressure contours at initial time |
为了考察网格光顺效果，本文选取单独采用RBF网格变形技术进行100个非定常时间步(约0.2s)后的瞬态网格，对其执行了150次光顺，从图 6可以看出，网格质量改善效果非常显著。
 |
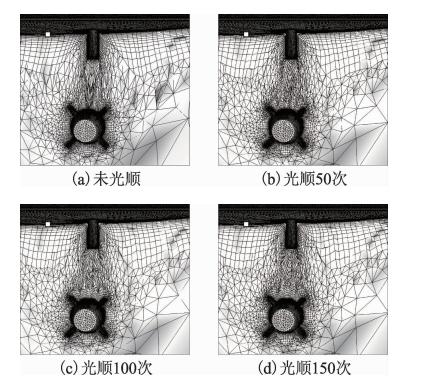| 图 6 光顺效果图Fig. 6 Effect of smooth |
由图 6可见，光顺次数越多，网格节点的整体分布越趋于均匀，意味着网格的质量越好，但耗费的计算时间也相应地增多。算例采用的参数设置是：从第50个非定常时间步开始启动光顺，每个非定常时间步执行10次光顺，初始松弛因子为0.5。单步动态混合网格的生成时间为459.856s，其中RBF网格变形耗时178.626s，10次光顺耗时281.23s。相比起一次非定常时间步的计算时间，一次动态混合网格的生成时间只占了很小的比例。
图 7给出外挂物投放过程中六个不同时刻的网格截面示意图。当外挂物与机翼之间的分离距离达到较大程度时，网格依然保持着良好的拓扑外形。
 |
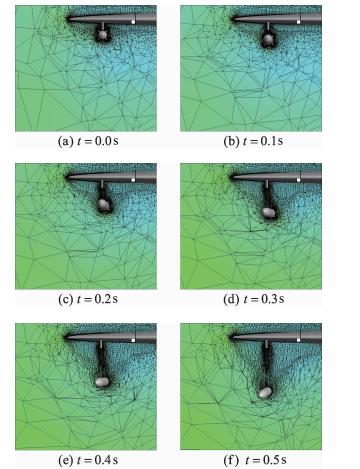| 图 7 分离过程网格变化示意图Fig. 7 Mesh slices of separation |
计算得到的投放过程中外挂物质心位移和姿态角与风洞实验的比较见图 8和图 9，总体上计算结果和实验值吻合很好。在图 8中，Xg、Yg、Zg表示质心位移，Z方向的质心位移匹配度最高，这是因为弹射力和重力在这个方向上远大于气动力，占了主要支配的地位。由于阻力的作用，外挂物会持续向后运动，CFD/RBD的仿真结果准确地反映了这一现象。在横侧向上，外挂物的质心会先略微向左，之后会缓慢地向右移动，这一点也与实验相符。
 |
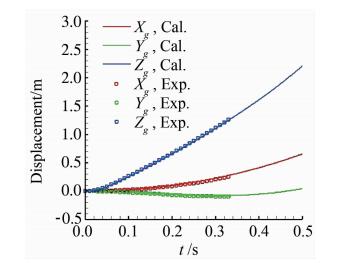| 图 8 质心位移与实验值的对比图Fig. 8 Calculated centeroid displacement vs. experiment |
 |
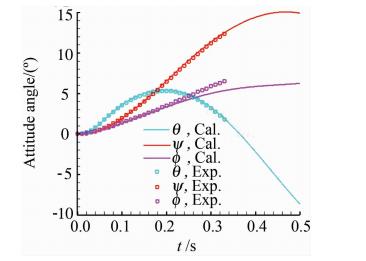| 图 9 姿态角与实验值的对比图Fig. 9 Calculated orientation angle vs. experiment |
图 9给出了三个姿态角随时间变化的结果。由图可知，俯仰角和偏航角和实验结果匹配良好。由于弹射力矩的作用，外挂物一开始会有一个抬头的效应，0.054s之后弹射力消失，俯仰力矩会逐渐使外挂物低头。外挂物在前0.5s左右先向右偏航，而后会逐渐左偏。本文的CFD/RBD轨迹仿真真实地反应了这些现象。外挂物在前0.5s一直是顺时针滚转的趋势，这一结果和实验一致。滚转角在0.3s后与实验值在数值上出现了一定的偏差，这是由于滚转惯性矩远远小于俯仰惯性矩和偏航惯性矩，这导致滚转角对于气动力的变化特别敏感，也使关于它的仿真变得尤其困难。
图 10和图 11是轨迹仿真过程中气动力和气动力矩随时间变化的示意图。从图中可以看出整个仿真过程中气动力和气动力矩与实验值的整体变化趋势吻合。图 10中X方向气动力略大，主要原因是实验中外挂物后部用尾撑杆支撑，略微抵消了气动阻尼的作用，使实验测得的气动力略小。
 |
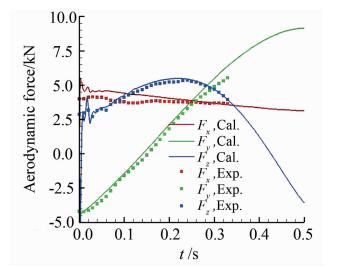| 图 10 气动力与实验值的对比图Fig. 10 Calculated aeroforces vs. experiment |
 |
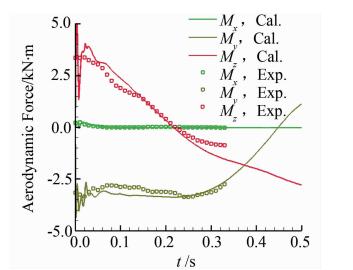| 图 11 气动力矩与实验值的对比图Fig. 11 Calculated aeromoments vs. experiment |
图 12给出外挂物在0.8s内与机翼和外挂物分离过程的示意图，可以更加直观形象地看到这个过程。此时的外挂物到机翼大约有一个展长的距离，边界之间的干扰已经基本可以被忽略，应可以对外挂物进行单体轨迹仿真。
 |
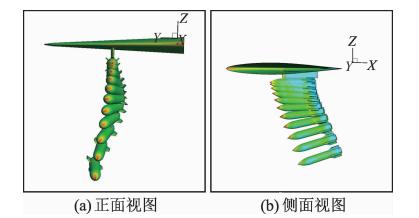| 图 12 机翼与外挂物分离过程示意图Fig. 12 Separation process of wing-store model |
本文以非结构混合网格为背景，针对四面体、三棱柱、六面体、金字塔四种网格单元提出了一套统一的网格质量评估标准，该质量评估标准可以准确统一地反映网格的质量。将上述质量标准作为光顺的执行判据，提出了一套改进的拉普拉斯网格光顺方法。
将上述网格光顺方法与径向基函数网格变形结合，形成了一种改进的RBF整体网格变形方法。在不进行网格重构和网格嵌套的前提下，该方法改善了单纯RBF网格变形技术所带来的网格质量下降和网格拓扑破坏问题，成功实现了多体分离中的超大幅度网格变形。
通过耦合求解非定常雷诺平均NS方程与六自由度方程，并采用以上改进的网格变形技术，实现了机翼外挂物分离轨迹仿真，证明本文网格变形方法具有很好的实用性。仿真结果与实验值对比吻合良好，验证了本文多体分离轨迹仿真方法的鲁棒性和精度。
| [1] | 郭正. 包含运动边界的多体非定常流场数值模拟方法研究[D].[博士学位论文]. 长沙:国防科学技术大学, 2002. |
| [2] | Wang Wei. Numerical simulation technique research and experiment verification for unsteady multi-body flowfield involving relative movement[D].[PhD. Thesis]. Changsha:National University of Defense Technology, 2002. (in Chinese)王巍. 有相对运动的多体分离过程非定常数值算法研究及实验验证[D]. 长沙:国防科学技术大学, 2008. |
| [3] | Duan Xupeng, Chang Xinghua, Zhang Laiping. A CFD-and-6DOF-coupled solver for multiple moving object problems based on dynamic bybrid grids[J]. Acta Aerodynamica Sinica, 2011,29(4):447-452. (in Chinese)段旭鹏, 常兴华, 张来平. 基于动态混合网格的多体分离数值模拟方法[J]. 空气动力学学报, 2011, 29(4):447-452. |
| [4] | Tian Shuling, Wu Yizhan, Xia Jian. 3D store separation simulation using unstructured overlapping grid[J]. Acta Aerodynamica Sinica, 2007, 25(2):245-249. (in Chinese)田书玲, 伍贻兆, 夏健. 基于非结构重叠网格的二维外挂物投放模拟[J]. 空气动力学学报, 2007, 25(2):245-249. |
| [5] | Gang Wang, Haris Hameed Mian, Zheng-Yin Ye, Jen-Der Lee. Improved point selection method for hybrid-unstructured mesh deformation using radial basis functions[J]. AIAA Journal, 2015, 53(4):1016-1025. |
| [6] | Baum J D, Lohner R. Three-dimensional store separation using a finite element solver and adaptive remeshing[C]//29th Aerospace Sciences Meeting, 1991-0602. |
| [7] | Zhang laiping, Deng Xiaogang, Zhang Hanxin. Reviews of moving grid generation techniques and numberical methods for unsteady flow[J]. Advances in Mechanics, 2010, 40(4):424-447. (in Chinese)张来平, 邓小刚, 张涵信. 动网格生成技术及非定常计算方法进展综述[J]. 力学进展, 2010, 40(4):424-447. |
| [8] | Heim E R. CFD wing/pylon/finned store mutual interference wind tunnel experiment[R]. Arnold Engineering Development Center, Arnold Afs Tn, 1991. |
| [9] | Wang G, Ye Z. Generation of three dimensional mixed and unstructured grids and its application in solving Navier-Stokes equations[J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(5):385-390.(in Chinese)王刚,叶正寅.三维非结构混合网格生成与N-S方程求解[J].航空学报,2003,24(5):385-390. |
| [10] | Jameson A. Time dependent calculations using multigrid, with applications to unsteady flows past airfoils and wings[C]//10th Computational Fluid Dynamics Conference, 1991-1596. |
| [11] | Gaitonde A L. A dual time method for the solution of the unsteady Euler equations[J]. Aeronautical Journal, 1994, 98(978):283-291. |
| [12] | Gao Hao, Zhu Peishen, Gao Zhenghong. The advanced flight dynamics[M]. Beijing:National Defence Industry Press, 2003. (in Chinese)高浩, 朱培申, 高正红. 高等飞行动力学[M]. 北京:国防工业出版社, 2003. |
| [13] | Sahu J. Time-accurate numerical prediction of free-flight aerodynamics of a finned projectile[J]. Journal of Spacecraft and Rockets, 2008, 45(5):946-954. |
| [14] | Jiang Yuewen, Ye Zhengyin, Zhang Weiwei. Semi-implicit solution of aeroelastic equations in time domain[J]. Engineering Mechanics, 2012, 29(4):66-71. (in Chinese)蒋跃文, 叶正寅, 张伟伟. 一种半隐式的气动弹性时域求解方法[J]. 工程力学, 2012, 29(4):66-71. |
| [15] | Field D A. Laplacian smoothing and Delaunay triangulations[J]. Communications in Applied Numerical Methods, 1988, 4(6):709-712. |
| [16] | Freitag L A, Knupp P M. Tetrahedral element shape optimization via the Jacobian determinant and condition number[C]//8th International Meshing Round Table, Lake Tahoe, 1999:247-258. |
| [17] | Lijewski L E, Suhs N E. Time-accurate computational fluid dynamics approach to transonic store separation trajectory prediction[J]. Journal of Aircraft, 1994, 31(4):886-891. |
| [18] | Panagiotopoulos E E, Kyparissis S D. CFD transonic store separation trajectory predictions with comparison to wind tunnel Investigations[J]. International Journal of Engineering, 2010, 3(6):538-553. |