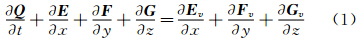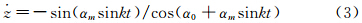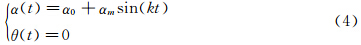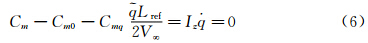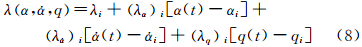0 引 言
吸气式内外流一体化飞行器因具有强突防、远航程及省时等优势而成为当前各国重点发展项目。相比其他传统飞行器而言，它能够提高推进效率、增强载荷能力、扩展发射窗口以及节省使用成本[1]。吸气式内外流一体化飞行器在助推器分离、进气道打开/关闭、燃烧室点火/熄火等过程面临扰动力矩带来的飞行姿态振荡问题[2]。进气道作为高超声速飞行器的关键部件，飞行姿态的非定常变化必然使进气道内部流动偏离设计工况，此时进气道是否还能正常启动，流场特征及性能如何变化，给下游燃烧室提供气流的品质如何，均是飞行器设计中需要探索的重要问题[3]。目前对高超声速内外流一体化飞行器的研究大多基于稳态，对非定常的进气道性能研究较为缺乏。为了实现动态运动的飞行器气动性能与发动机推进性能之间的耦合研究，复杂内流流动的非定常气动特性是飞行器设计中必须考虑的重要因素。
动导数广泛应用于飞行器在扰动(包括控制面作用)下的动态稳定性研究之中。通过飞行器绕定轴的振动可以获得俯仰阻尼导数等直接阻尼导数。直接阻尼导数是旋转导数和加速度导数的组合。目前动导数的计算和实验对直接阻尼导数关注较多。在工程应用中旋转导数和加速度导数一般采用设定比例从直接阻尼导数中得到，但现代飞行器外形设计和运动方式比传统飞行器复杂，流动的非线性及非定常性更强，上述方法是否适用，值得进一步讨论。研究表明，对某些飞行器来说反映流动时滞效应的加速度导数占直接阻尼导数的比例可以达到40%~50%，而在某些情况加速度导数所占比例很小，甚至与直接阻尼导数符号相反[4, 5]。因此，作为飞行稳定性研究的重要参数，旋转导数和加速度导数也是动导数预测研究的重要内容。
本文在标模验证的基础上开展吸气式内外流一体化飞行器动态特性分析。采用三维雷诺平均的RANS方程模拟飞行器强迫简谐振动的非定常流场，开展非定常运动对动态气动特性的影响研究。针对飞行器直接阻尼导数，特别是旋转导数和加速度导数，开展多种模拟方法研究。在此基础上还对基于动导数的非定常参数拟合方法进行了分析对比。 1 控制方程及离散方法
在贴体坐标系下，完全气体、忽略质量力下的三维无量纲Navier-Stokes方程形式如下：
式中：Q为守恒变量，E、F、G为对流通量，Ev、Fv、Gv为粘性通量。
本文采用二阶迎风型NND格式有限体积离散流动控制方程组的空间导数项，采用含双时间步的LU-SGS方法来提高时间求解的效率和精度。湍流模型采用基于工程经验和量纲分析的SA模型。远场边界采用适用于动态边界条件下的一维Riemann不变量的无反射边界条件。壁面边界、速度采用无滑移条件，温度采用绝热壁条件，压力条件计入离心力的影响。 2 动导数数值预测方法
通过绕定轴的非定常强迫简谐振动可以获得直接阻尼导数。加速度导数代表飞行器做沉浮运动或洗流(上洗或下洗)的延迟效应及非定常涡的时间迟滞特性[4, 6]，通过飞行器的沉浮或侧滑运动可以获得加速度导数。旋转导数表示姿态角速度的变化引起飞行器表面与来流夹角的局部变化而产生的附加气动特性，具有准定常特性[7]，既可以通过非定常强迫拍动运动获得，也可以通过准定常方法求解。 2.1 强迫简谐振动法
图 1是飞行器三种非定常强迫简谐振动(俯仰/沉浮/拍动)的飞行姿态和运动轨迹示意图。
 |
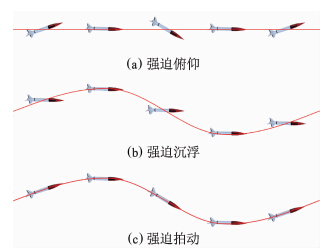| 图 1 非定常运动示意图Fig. 1 Sketch of unsteady motion |
强迫俯仰简谐振动(图 1(a))用于计算俯仰直接阻尼导数Cmq+Cm，其振动方程为：
式中，α0为初始攻角，θm为俯仰角振幅，k为无量纲减缩频率(k=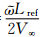
，其中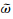
为圆频率，Lref为参考长度，V∞为来流速度)。
采用文献 发展的强迫沉浮简谐振动(图 1(b))方法计算俯仰力矩加速度 导数Cm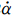
。通过给定垂直方向沉浮运动速度
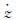的形式，实现强迫沉浮振动：
强迫沉浮振动方程为：
强迫拍动简谐振动(图 1(c))用于计算俯仰力矩旋转导数Cmq。通过绕定轴的强迫振动叠加沉浮振动可以得到强迫拍动振动方程为：
基于Etkin模型[6]，通过上式对计算产生的时域数据进行后处理来辨识得到动导数，具体的推导过程见文献[8]。
2.2 准定常方法旋转导数除了采用强迫简谐振动法模拟外，还可以采用准定常方法得到。旋转导数表示姿态角速度的变化引起飞行器表面与来流夹角的局部变化而产生的附加气动特性[9]。飞行器在攻角不变时绕z轴以恒定俯仰角速度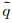
转动时的平衡方程为：
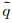转动时攻角α处的俯仰力矩系数，Cm0为俯仰角速度为0时攻角α处的俯仰力矩系数，Iz为绕z轴的转动惯量，
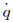为角加速度(匀角速度旋转时为0)。
Cm0可以通过定常计算获得。在准定常假设下，Cm的计算需要考虑俯仰角速度引起的牵连速度的影响以反映局部迎角的变化。在空间格式及壁面边界条件中加入牵连速度的贡献，经时间推进得到收敛的俯仰力矩系数Cm。由式(6)可得
准定常方法能够快速方便地求解旋转导数，其计算效率与定常方法大致相等。本文针对动导数标模外形和吸气式内外流一体化外形，采用准定常方法求解旋转导数，并与完全非定常计算结果进行了对比验证。 3 验证算例
目前，国内外高超声速动导数标模外形主要包括HBS(Hyper Ballistic Shape)导弹标模、Finner“十”字翼标模以及ANSR(Army-Navy spinner rocket)旋转稳定式火箭弹标模。HBS和Finner标模有组合导数Cmq+Cm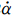的风洞实验结果。文献[8]中给出了上一节强迫俯仰简谐振动计算的组合导数，实验与计算结果取得了较好的一致。国外针对ANSR火箭弹外形开展了组合导数、加速度导数及旋转导数等一系列纵向动态稳定性导数的实验与计算[10, 11, 12, 13]。本节将采用ANSR标模针对俯仰力矩导数Cmq、Cm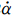、Cmq+Cm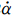及法向力导数CNq、CN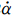、CNq+CN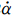开展计算验证。
5口径与9口径ANSR标模尺寸如图 2所示，1口径长度代表 20mm。分别对两个标模选择了三个不同的质心位置xc.g.(见表 1)，考察了质心位置对各种阻尼导数的影响。
 |
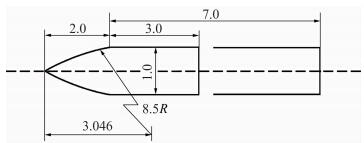| 图 2 ANSR标模尺寸(单位：口径，1口径=20mm)Fig. 2 ANSR dimensions(unit: caliber,1cal.=20mm) |
| 标模长度 | 质心位置xc.g. | ||
| 5口径 | 2.5 | 3.0 | 3.5 |
| 9口径 | 4.0 | 5.038 | 5.885 |
三维计算网格采用对称面网格旋转生成。弹身附近的对称面网格及拓扑结构如图 3所示。5口径与9口径ANSR标模网格量分别为27.5万和29.6万。壁面处第一层法向网格尺度为10-5D，D为弹身直径，最小网格雷诺数在10左右。头部附近的网格拉伸比控制在1.1以下。所有的算例的马赫数为2.5，初始攻角和侧滑角均为0°，自由来流条件取标准大气下的海平面条件(101.325kPa,288K)。强迫振动的振幅为1°，无量纲减缩频率k取0.1。
 |
| 图 3 ANSR对称面网格拓扑Fig. 3 ANSR symmetric plane mesh topology |
表 2给出了ANSR标模俯仰力矩系数的旋转导数。表中Cmq(1)为采用式(7)准定常计算结果，Cmq(2)为采用式(5)完全非定常的强迫简谐振动法的计算结果。Cmq(3)为采用完全非定常的强迫简谐振动法计算得到的Cm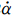+Cmq与加速度导数Cm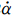相减得到的结果。表中采用diff.表示三者中的最大值和最小值之差与三者平均值比值的绝对值，可以看出三者之间的最大差别不超过4%。说明不同方式计算得到的旋转导数差别不大，分别计算的加速度导数和旋转导数之和与直接计算得到的组合导数相等。由于准定常方法计算效率与定常计算相同，计算开销明显小于非定常方法，因此下文中均采用准定常方法计算得到旋转导数。
| 标模长度 | xc.g. | Cmq(1) | Cmq(2) | Cmq(3) | diff. |
| 5口径 | 2.5 | -17.65 | -17.89 | -17.78 | 1.4% |
| 3.0 | -18.85 | -19.39 | -18.85 | 2.8% | |
| 3.5 | -23.27 | -24.13 | -23.67 | 3.6% | |
| 9口径 | 4.0 | -88.33 | -88.04 | -88.01 | 0.4% |
| 5.038 | -94.93 | -94.90 | -95.38 | 0.5% | |
| 5.885 | -111.11 | -111.63 | -111.23 | 0.5% |
图 4给出了针对ANSR标模纵向动导数本文计算结果(CFD)、文献[13]计算结果(PNS、SBT)以及文献[11]实验结果(EXP)的比较。其中PNS为英国的Qin及美国军队研究实验室(ARL)的Paul Weinacht等人采用抛物化的NS方程在非惯性系中求解锥运动和螺旋运动得到的纵向动态稳定性导数[13]。这种方法好处是效率较高，可直接得到组合导数的分量形式(加速度导数和旋转导数)，但该方法有其局限性，只适用于轴对称或面对称外形的小攻角线性状态，且仅能够计算俯仰和偏航通道。图中SBT(Slender Body Theory)为采用工程近似方法中细长体理论得到的结果[13]，除了图 4(a)中质心位置取2.5口径时各项俯仰力矩导数与CFD计算一致外，采用SBT方法的其余状态均有量级甚至符号的差别。图中EXP为美国陆军弹道研究实验室俯仰力矩组合导数的实验结果[11]，同条件下的实验的数据之间具有一定的散布度。工程方法SBT在动导数的预测趋势上与实验符合，但数值上差别较大。PNS方法和本文CFD计算与实验数据基本一致，说明了本文动导数计算方法的合理性。
 |
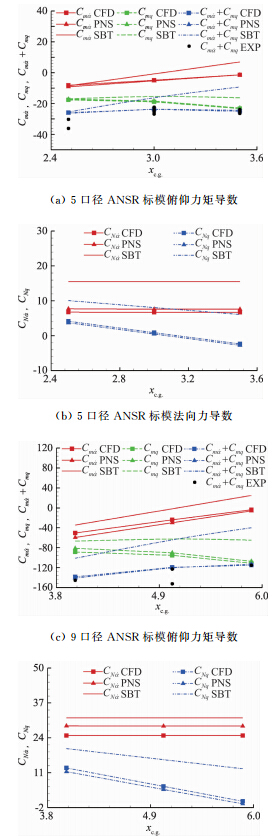| 图 4 ANSR标模纵向动导数随质心变化规律Fig. 4 ANSR longitudinal dynamic derivatives variation as a function of center of mass |
对ANSR标模俯仰力矩导数来说，反映流动时滞效应的加速度导数占组合导数的比例变化范围很大，图 4(c)中xc.g.=4.0时的比例能够达到42%。随着质心后移加速度导数所占比例逐渐减小，图 4(c)中xc.g.=5.885时的比例仅为3%；对ANSR标模法向力导数来说，旋转导数与质心位置成近似线性关系，加速度导数则不受质心位置的影响，加速度导数占组合导数的比例大于旋转导数。
4 WR-A外形静、动态气动特性研究 4.1 WR-A外形吸气式高超声速巡航导弹WR-A(Wave Rider)的气动外形是本文仿照美国气动/推进一体化设计方案X-51A乘波飞行器[14]设计而成，其外形如图 5(a)所示。表 3给出了WR-A和X-51A两种外形几何尺寸的对比。X-51A弹道设计包括助推段、爬升段、巡航段、俯冲段，本文重点针对X-51A转级点(助推器分离：Ma=4.8，H=18 288km)和设计点(巡航状态：Ma=6.5，H=24 384km)两个典型弹道位置开展动态导数研究。
 |
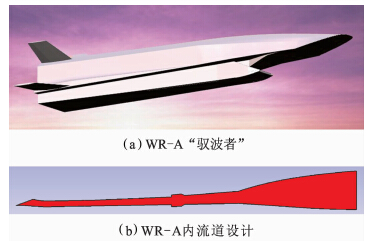| 图 5 WR-A外形示意图Fig. 5 WR-A layout |
| 飞行器总长L | 最大宽度 | 长细比 | 发动机内流道宽度 | |
| X-51A | 4.2672m | 0.5842m | 7.3 | 0.2286m |
| WR-A | 4.2672m | 0.5842m | 7.3 | 0.2286m |
WR-A乘波飞行器采用乘波体反向设计方法[15, 16]设计出的楔锥形乘波构型[17, 18]。外压缩段采用多道斜激波压缩加等熵波压缩的波系配置形式，内压缩段设计采用混压式矩形截面进气道。隔离段设计采用略有扩张的矩形管道。燃烧室采用开式火焰稳定凹腔，长度0.1193m，深度0.0178m，长深比6.7，后缘角30°。WR-A内流道设计如图 5(b)所示。
4.2 WR-A静态气动特性针对乘波体WR-A的转级点和设计点开展了冷流状态下静态气动特性计算，并与X-51A气动性能进行比较。此外，静态流场计算结果作为动态非定常计算的初始流场，可以加速非定常流场的收敛，提高计算效率与精度。 4.2.1 网格划分
根据吸气式内外流一体化外形特点，本文采用“O-H”型拓扑生成三维结构化网格(见图 6)，网格总量为4271万，共划分为208块。内外流一体化外形表面存在很强的压缩、剪切现象及边界层干扰等因素引起的较大摩擦阻力，乘波体WR-A的数值模拟显示，该部分摩阻在总阻力中所占比重能够达到50％以上。乘波体WR-A壁面处第一层法向网格尺度量级为10-7L，网格拉伸比控制在1.1以下。边界层网格的细致刻化是壁面附近速度梯度即粘性计算准确度的重要保证。
 |
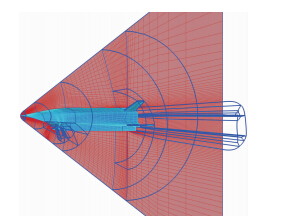| 图 6 WR-A对称面网格及拓扑结构Fig. 6 Symmetric plane mesh and topological structure of WR-A |
对于乘波体构型机身而言，前体几何的精确设计和激波系的结构布置是非常重要的。本文WR-A乘波体前体压缩面按马赫数6.5设计点的斜激波交于唇口处设计，如图 7所示。来流在进气道唇口处减速至马赫数4左右，下表面产生一道斜激波和上表面的边界层发生干扰，产生边界层分离。分离与反射激波打到进气道下表面后不断向下游折射发展。图 8给出了燃烧室和喷管段流动的发展过程。燃烧室凹腔处产生流动分离，几道斜激波之间相互交叉干扰。喷管处流动开始膨胀加速，马赫数最高达到6.8左右。
 |
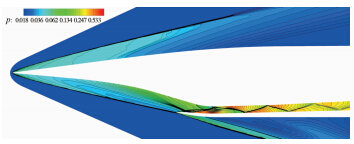| 图 7 头部对称面压力云图Fig. 7 Pressure cloud of head symmetric plane |
 |
| 图 8 燃烧室及尾喷管对称面压力云图Fig. 8 Pressure cloud of combustion chamber and nozzle symmetric plane |
转级点与设计点的升阻比随攻角的变化曲线如图 9所示。图中还给出了美国空军研究室会议报告公布的X-51A气动特性的数值结果[19]，做为本文计算结果的参考。WR-A转级点与设计点的升阻比在攻角范围-4°至4°内升阻比近似线性，攻角超过此范围后升阻比存在极值。通过与美国X-51A气动特性的比较，本文建立的WR-A模型气动性能符合典型高升阻比乘波体／升力体气动特征。
 |
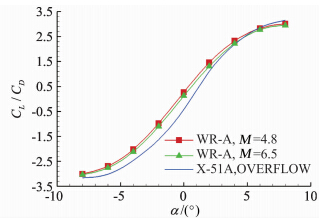| 图 9 WR-A乘波体升阻比与X-51A对比Fig. 9 Comparison of lift-drag ratio between WR-A waverider and X-51A |
针对乘波体WR-A的设计点在0°至8°攻角范围内开展俯仰方向直接导数、加速度导数及旋转导数数值模拟。在此基础上开展基于参数化动导数概念下的非定常气动参数建模研究。
4.3.1 设计点纵向动态攻角特性分析采用绕定轴的强迫俯仰简谐振动和沉浮运动分别获得直接阻尼导数和加速度导数。强迫振动的振幅αm为1°，振动频率f为5Hz。当在初始瞬值衰变之后，流场参数及气动荷载达到谐振状态。图 10给出了0°攻角的俯仰力矩系数Cm及进气道性能参数的时间历程曲线，其中压升比Rp、总压恢复系数σ和流量系数φ均为隔离段入口截面上的质量加权平均值。由于非定常计算采用静态流场作为初场，收敛速度很快，在不到半个周期内初始瞬值衰变完成，流场达到谐振状态。
 |
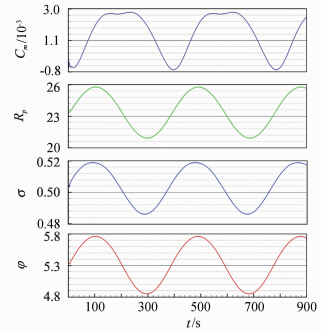| 图 10 俯仰力矩系数及进气道性能参数的时间历程曲线Fig. 10 Time history of pitch moment coefficient and air inlet performance parameters |
飞行器的非定常运动使得进气道内部流场处于动态变化的状态。此时针对内流流场特征及性能变化的预测非常重要。例如压升比Rp反映了进气道抗反压的能力，如果动态非定常运动过程中Rp下降，则有可能导致燃烧室反压对进气道产生干扰而进入不启动状态。2011年X-51高超声速飞行器第二次飞行实验中就是因为超燃冲压发动机的进气道未能启动而导致失败[20]。目前对进气道性能的计算主要还是针对稳态，本文则根据Etkin理论，采用与力矩导数相同的方式对进气道性能参数导数进行求解，可以用于动态非定常时进气道性能的预测，为飞行器进排气系统与控制系统耦合问题的解决提供相应的气动参数。
图 11给出了俯仰力矩系数及进气道性能参数的动导数预测结果。通过绕定轴的强迫俯仰振动，可以得到不同气动参数λ的俯仰导数λq+λ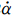。通过沉浮运动，得到加速度导数λ 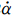。通过准定常计算，得到旋转导数λq。将准定常计算出的旋转导数与加速度导数相加得到(λq)+(λ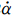)。其中λ代表俯仰力矩系数Cm、压升比Rp、总压恢复系数σ和流量系数φ。图 11中不同攻角下λq+λ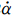与(λq)+(λ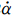)基本相等。对图 11(a)中俯仰力矩系数来说，在攻角4°和6°时加速度导数与组合导数符号相反，起不稳定的作用。图 11(a)中旋转导数曲线与组合导数曲线十分靠近，加速度导数占组合导数的比例较低，最大不超过20%，反映出WR-A飞行器做沉浮运动的延迟效应及非定常涡的时间迟滞特性较弱。进气道性能参数的加速度导数则与之相反，如图 11(b)~图 11(d)所示，加速度导数曲线更加接近组合导数曲线，占组合导数的比例普遍高于旋转导数，说明非定常效应对进气道性能参数变化的影响主要来自于非定常流场的时滞效应。
 |
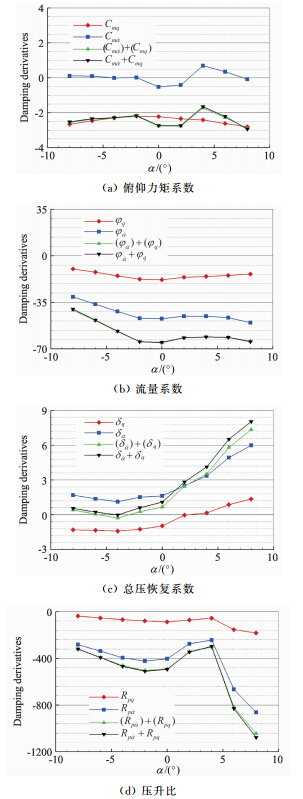| 图 11 俯仰力矩系数及进气道性能参数的动导数预测结果Fig. 11 Dynamic derivative predictions of pitch moment coefficient and air inlet performance parameters |
不同攻角下绕定轴的强迫俯仰振动和沉浮运动俯仰力矩系数的迟滞环曲线如图 12所示。迟滞环的倾斜形状、面积及旋转方向决定了动导数的大小与符号。由于WR-A乘波体定常状态的俯仰力矩系数具有较强的非线性特征，因此图 12中动态条件下的迟滞环并不全是倾斜光滑的椭圆形状。迟滞环面积表示乘波体振动过程中环境对其做功的大小，WR-A乘波体沉浮运动的迟滞环面积明显小于俯仰振动，这与图 11(b)中阻尼大小的规律相一致。图 12中还用箭头标出了沉浮运动迟滞环的旋转方向。迟滞环的旋转方向表示做功的方向，逆时针旋转表示乘波体对环境做功，消耗乘波体动能，对动导数的贡献为负值，起动稳定作用。顺时针表示环境对乘波体做功，乘波体动能增加，对动导数的贡献为正值，起不稳定作用。WR-A飞行器沉浮运动的迟滞环在攻角2°和4°时变换方向，在6°和8°时呈8字环运动，说明飞行器的加速度导数经历了三次变号。从迟滞环图中可以看出WR-A飞行器的加速度导数在攻角3°至6.2°和大于7.8°攻角的范围起不稳定作用。
 |
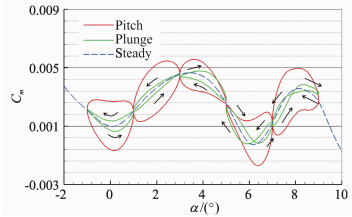| 图 12 强迫俯仰振动和沉浮运动俯仰力矩系数迟滞环Fig. 12 Pitch moment coefficient hysteresis loop of forced pitch vibration and plunge motion |
图 13给出了总压恢复系数在不同攻角下绕定轴的强迫俯仰振动和沉浮运动的迟滞环曲线。随着攻角的增加，进气道前缘压缩激波的强度增加，外压段压缩能力增强，外压波系后的马赫数降低。当攻角从负攻角上升至1.5°时，内流道激波边界层干扰效应降低，进气道出口总压恢复性能增加。当攻角从1.5°继续上升时，多波系压缩的外压段产生激波干扰作用，进气道边界层增厚，从而在一定程度上降低进气道流量捕获能力并使出口总压恢复性能降低。
 |
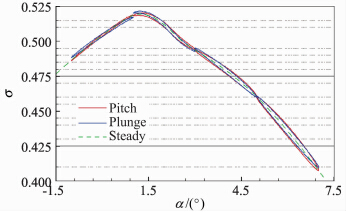| 图 13 强迫俯仰振动和沉浮运动总压恢复系数迟滞环Fig. 13 Total pressure recovery coefficient hysteresis loop of force pitch vibration and plunge motion |
非定常气动力的建模方法一直是空气动力学的重要研究内容。当飞行器在小攻角条件下飞行时，流动以附着流型为主，气动力与运动状态参数常常成线性关系，因此动导数可看成是常数，可简单得到非定常气动力的拟合结果。现代飞行器外形设计和运动方式比传统飞行器复杂，大攻角和非零侧滑角的飞行状态通常会引起非常复杂的气动现象，激波诱导分离、旋涡运动与破裂以及它们的相互作用使得流体运动呈现强烈的非定常、非线性特征。动导数不再是常数，而是和攻角、侧滑角、减缩频率等参数相关，具有参数化的性质。为了更好地描述动态特性在大攻角时出现的非线性特征，本节采用参数化的动导数概念建立非定常气动参数模型。通过对比气动参数模型与采用完全非定常计算得到的大振幅强迫振动的非线性气动力结果，开展WR-A飞行器非定常气动参数拟合方法研究。
WR-A乘波体在设计点位置大振幅强迫运动的基准攻角为0°，振幅为1°至8°，频率为5Hz。对于作俯仰运动的飞行器，决定绕俯仰轴转动运动的状态变量为α、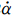和q。动导数是状态变量α的函数。本文首先在前述工作基础上计算出i(i=0,±1,±2,…,±8)攻角下的静态与动态气动参数λi、(λα)i、(λ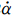)i、(λq)i，其中λ代表气动力系数或进气道性能参数。当攻角α处于[i－0.5,i+0.5]区间内时，λ的表达式为：
图 14中的曲线为采用完全非定常计算得到的俯仰力矩系数和进气道性能参数的迟滞环。图 14中的数据点表示采用参数化的动导数概念建立的气动模型计算得到的俯仰力矩系数Cms、压升比Rps、总压恢复系数σs和流量系数φs。当攻角小于0°时，采用式(8)计算得到的Cms全部准确地落在不同振幅下的俯仰力矩迟滞曲线上。当攻角大于0°时，俯仰力矩系数曲线开始出现较为明显的非线性特征，图 14(a)中4°振幅以内的Cms与迟滞曲线符合较好。振幅6°和8°的Cms与迟滞曲线有一定差别，但趋势上与迟滞曲线相同。说明对俯仰力矩系数而言，当运动处于非线性特性较弱的区域时(攻角-8°至-2°)，参数化的动导数概念建立的气动模型预测大攻角的气动数据与非定常计算符合较好。当运动处于非线性特性较强的区域时(0°攻角以上)，大攻角的气动数据与非定常计算有一定偏差，总体吻合较好。
 |
| 图 14 大攻角振动迟滞环曲线Fig. 14 Hysteresis loop curve of large-amplitude vibration |
图 14(b)~图 14(d)给出了动导数模型预测进气道性能参数时的特性曲线。与俯仰力矩系数不同的是，无论运动处于正攻角或负攻角范围，采用参数化的动导数概念建立的气动模型预测的进气道性能参数与非定常计算一致。图 14(b)和图 14(d)中的流量系数和压升比随着攻角的上升呈线性增加的趋势。图 14(c)中总压恢复系数则在1.5°攻角处增大到极值位置，然后逐渐减小。在负攻角范围内，总压恢复系数的滞后特性微弱，迟滞环的上行程和下行程几乎重合。当飞行器攻角大于0°时，总压恢复系数的滞后效应开始变得明显，迟滞环曲线在攻角越大的位置越显得“丰满”，总压恢复系数导数的绝对值也逐渐增大，与图 11(c)所反映的规律一致。
5 结 论本文在标模验证的基础上开展吸气式内外流一体化飞行器动态特性分析。采用三维雷诺平均的RANS方程模拟飞行器强迫简谐振动的非定常流场，通过建立不同的强迫简谐振动模式，获得了直接阻尼导数、加速度导数和旋转导数的辨识方法。并在此基础上得到的主要结论如下：
对俯仰力矩系数的加速度导数来说，WR-A乘波体的加速度导数占组合导数的比例较低，最大不超过20%，最小时与组合导数符号相反。而ANSR火箭弹的加速度导数所占比例变化范围很大，最高能够达到40%以上，最低仅为3%。
基于Etkin理论对进气道性能参数动态导数进行求解，用于分析非定常内流流场特性。WR-A乘波体进气道性能参数的加速度导数占组合导数的比例大于旋转导数，说明非定常效应对进气道性能参数变化的影响主要来自于非定常流场的时滞效应。
初步开展了参数化动导数概念下的非定常气动参数建模研究。采用所建立的模型预测WR-A乘波体在大攻角时的俯仰力矩系数，在非线性特性较弱的区域与非定常计算符合较好，在非线性特性较强的区域则产生一定偏差，非定常气动参数模型预测的大攻角条件下的进气道性能参数与非定常计算吻合较好。
| [1] | Bilaedo V J, Curran F M, Hunt J L, et al. The benefits of hypersonic airbreathing launch systems for access to space[R]. AIAA 2003-5265. |
| [2] | Mirmirani M D, Wu C, Clark A, et al. Modeling for control of a generic airbreathing hypersonic vehicle[C]//Proceedings of AIAA Conference on Guidance, Navigation, and Control Conference, 2005. |
| [3] | Bahm C, Baumann E, Martin J, et al. The X-43A Hyper-X Mach 7 flight 2 guidance, navigation, and control overview and flight test results[R]. AIAA 2005-3275. |
| [4] | Liu W, Yang X L, Zhao Y F. Numerical simulation of acceleration derivative of hypersonic aircraft[J]. Acta Aerodynamica Sinica, 2010, (04):426-429. (in Chinese)刘伟, 杨小亮, 赵云飞. 高超声速飞行器加速度导数数值模拟[J]. 空气动力学学报, 2010, (04):426-429. |
| [5] | Sun H S. A measurement technique for derivatives of aircraft due to acceleration in heave and sideslip at high angle of attack[J]. Experiments and Measurements in Fluid Mechanics, 2001, 15(4):15-19. (in Chinese)孙海生. 飞行器大攻角升沉平移加速度导数测量技术[J]. 流体力学实验与测量, 2001, 15(4):15-19. |
| [6] | Etkin B. Dynamics of atmospheric flight[M]. Courier Dover Publications, 2012. |
| [7] | Bergmann A, Hübner A. Integrated experimental and numerical research on the aerodynamics of unsteady moving aircraft:proceedings of the 3rd international symposium on integrating CFD and experiments in aerodynamics[R]. U. S. Air Force Academy, CO, USA, 2007. |
| [8] | Liu X. Investigation of dynamic characteristics of hypersonic airframe/propulsion integrative vehicle[D]. Changsha:National University of Defense Technology, 2011. 刘绪. 高超声速内外流一体化飞行器动态特性研究[D]. 长沙:国防科学技术大学, 2011. (in Chinese) |
| [9] | Xi K, Yan C, Huang Y, et al. Numerical simulation of individual components of pitch-damping coefficient sum[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(2):222-227. (in Chinese)席柯, 阎超, 黄宇, 等. 俯仰阻尼导数分量的 CFD 数值模拟[J]. 北京航空航天大学学报, 2015, 41(2):222-227. |
| [10] | DeSpirito J, Silton S I, Weinacht P. Navier-Stokes predictions of dynamic stability derivatives:evaluation of steady-state methods[J]. Journal of Spacecraft and Rockets, 2009, 46(6):1142-1154. |
| [11] | Murphy C H, Schmidt L E. The effect of length on the aerodynamics characteristics of bodies of revolution in supersonic flight[R]. U. S. Army Ballistic Research Lab., Rept. 876, 1953. |
| [12] | Schmidt L, Murphy C. The aerodynamic properties of the 7-caliber army-navy spinner rocket in transonic flight[R]. U. S. Army Ballistic Research Lab., BRL-MR-775, 1954. |
| [13] | Weinacht P, Sturek W B, Schiff L B. Navier-Stokes predictions of pitch damping for axisymmetric projectiles[J]. Journal of Spacecraft and Rockets, 1997, 34(6):753-761. |
| [14] | Hank J M, Murphy J S, Mutzman R C. The X-51A scramjet engine flight demonstration program[R]. AIAA 2008-2540. |
| [15] | Kuchemann D. The aerodynamic design of aircraft[M]. AIAA Education Series, Amer Inst of Aeronautics and Astronautics, 2012. |
| [16] | Bauer S. Analysis of two viscous optimized waveriders[C]//Proceeding of First International Hypersonic Waverider Symposium, 1990. |
| [17] | Takashima N, Lewis M J. Waverider configurations based on non-axisymmetric flow fields for engine-airframe integration[C]//Proceedings of 32nd Aerospace Sciences Meeting and Exhibit. Reno, NV, 1994. |
| [18] | Wang Zhuo. High speed flow design using the theory of osculating cones and axisymmetric flows[J]. Chinese Journal of Aeronautics, 1999, (01):3-10. |
| [19] | Mutzman R, Murphy S. X-51 development:a chief engineer's perspective[C]//Proceedings of the 17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference. 2011. |
| [20] | Bai Y L, Bai Y. Failure analysis of X-51A aircraft flight test[J]. Cruise Missile, 2012, (3):27-31. (in Chinese)白延隆, 白云. X-51A 飞行器飞行试验的故障分析[J]. 飞航导弹, 2012, (3):27-31. |