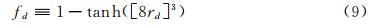随着民用飞机数量的快速增加和普及，航空噪声问题日益引起世界范围内的广泛关注。噪声水平已经成为检验飞机试航条例的重要指标之一。噪声对 于乘客舒适性的影响也直接关系到飞机的市场竞争 力。如何使设计的飞机符合噪声适航条例和满足座舱噪声水平的要求成为航空工业发展的重要问题。
发动机噪声和机体噪声是飞机噪声的两个最主要来源。随着更高涵道比发动机的诞生和“安静”发动机技术的应用，发动机的噪声水平将降低到与机体噪声同等甚至更低水平。机体噪声包括增升装置噪声和起落架噪声等。早期气动噪声研究集中在分析增升装置噪声，随着研究的深入，更具挑战的起落架噪声研究开始受到重视。起落架的总噪声由低频、中频和高频噪声三部分叠加而成。这三部分噪声分别由不同特征尺寸的起落架构件模型产生：机轮产生低频噪声；支柱、斜撑杆、轮轴等产生中频噪声；台阶、突起和导线等细节部分产生高频噪声[1]。
复杂的几何外形以及与空气动力的相互作用所形成的复杂气流流场结构，给起落架噪声的理论和试验研究带来了很多困难。由于起落架外形复杂、与周围流体相互作用剧烈，以及形成的声波频带范围宽、传播范围广、能量相对较小等因素，造成起落架噪声的数值模拟与试验研究均比较困难。迄今为止，起落架噪声问题仍是机体噪声研究的难点之一[2]。
由于对数值格式的要求极为苛刻(低频散、低耗散)，并且最小网格需要捕捉到高频声源的波长，直接求解远场声场的方法所需的计算量很大，在可预见的未来尚无法用于工程设计。从20世纪60年代起，随着气动声学经典理论的发展，Lighthill声比拟理论及FW-H方程被广泛地用于气动声学问题研究[3]。该方法的基本思想是基于计算流体力学(CFD)方法计算获得运动物面的非定常压力分布，然后基于求解FW-H方程(或Kirchhoff方法)获得远近声场分布。
声比拟方法依赖于对近场非定常流动的准确预测。基于定常雷诺平均NS方程(Reynolds Averaged Navier-Stokes，RANS)的声学比拟方法首先通过湍流模型求解，得到定常流场以及用于噪声计算的流场信息文件。在此基础上通过非定常求解器NLAS求解物面附近的声场信息。同时采用FW-H方程得到远场的声场信息。这类方法对湍流流动所作假设较多，计算精度受到一定影响。而绕起落架的流动由于其本身几何外形的复杂，存在一系列复杂的物理现象，如大片低速区域、强压力梯度、非定常流动区域、三维效应以及边界层与尾流区的相互干扰等等，这些现象难以用定常RANS方程刻画。因此，在计算资源许可的情况下，可以保留RANS方程中的时间项，直接求解非定常流场，即非定常RANS(URANS)。近年来，比URANS更先进的分离涡模拟(DES)类方法在起落架气动噪声的计算中得到越来越多的应用，而我国学者在这方面的工作处于世界前列。龙双丽等[4]使用DES进行了某型起落架的气动噪声计算，并使用FW-H积分得到了远场噪声分布。为了解决DES存在的提前分离问题，又发展了延迟的分离涡模拟(DDES)等方法，如肖志祥等[5]使用基于SST二方程湍流模型的DDES和改进的DDES(IDDES)研究了基本起落架的流场和近场噪声，发现DDES能够得到很好的结果，而IDDES并未比DDES更优。因此，在上述各种非定常解算方法之间还需要更多全面的比较，以便为工程人员提供选择依据。
对非定常CFD方法的选择需要考虑研究对象、计算条件、数值方法等因素。URANS方法鲁棒性最好，但对远场湍流脉动的耗散比较严重；DES的耗散性适中，应用较为成熟与广泛；DDES由于能够修正提前分离问题，比起DES有一定的理论优势。IDDES使用的经验函数过多，在工程应用中的普适性尚未得到全面验证；并且IDDES比起DDES的改进主要在附着流动的预测[6]，对于起落架这样的大分离流动，IDDES没有明显的优势。本文采用URANS、DES以及DDES互相对照,对基本起落架绕流进行数值模拟，并对其流场的非定常特性进行分析，提取声源的强度和分布信息，为研究起落架气动噪声机理、探索起落架气动噪声的预测方法以及探索起落架噪声控制策略提供参考。 1 外形、边界条件及网格划分
基本起落架是2010年斯德哥尔摩机体噪声计算会议[7]的标模，包括四个起落架轮和矩形截面的轮轴以及轮架。图 1给出了基本起落架模型的几何参数，该几何外形与Ventakrishnam 等[8]的试验所用外形一致。以轮直径为1，则轮宽为0.37，轮边缘曲率半径0.115，前后轮间距1.16，辙距0.88；横轴截面为正方形，边长0.3，横梁截面为长方形，高0.3、宽0.25，垂直支架为正方形截面，边长0.25。模型安放在边长为3.69的矩形截面风洞中央，计算域入口与模型距离为3，出口与模型距离为7。
文中采用的计算网格见图 2、3 。网格类型为多块结构网格，使用商业软件ICEMCFD生成。网格单元数约为1200万。在计算中，只有机体采用无滑移条件。风洞壁采用的是滑移边界条件，因此在洞壁附近没有边界层网格。入口与出口采用来流条件，来流马赫数为0.115，恰好对应试验中所用的风速40m/s。基于轮直径的雷诺数为1×106。
 |
| 图 2 计算网格水平截面图 Fig. 2 Profile of simulation mesh |
 |
| 图 3 表面网格 Fig. 3 Surface mesh |
数值计算基于中国航天空气动力技术研究院自 主研发的气动计算平台NS-Solver[10]进行，采用 Navier-Stokes方程作为流动控制方程，空间离散采用有限体积方法。控制方程的积分形式为
式(1)中，Ω为控制体，W为守恒变量，H=(f-fv,g-gv,h-hv)为通过表面Ω的无粘通量和粘性通量。
通常在RANS计算中，对无粘通量项进行离散采用迎风型的Roe格式。这是RANS计算的常用格式，主要优点是稳定性好，但数值耗散较大。Spalart[11]建议为了更好地捕捉流场中大尺度旋涡的非定常动力学，需要采用低耗散的数值格式。因此，本文计算中采用了中心格式。中心格式使用的人工耗散
耗散系数
为了减小数值耗散的影响，希望耗散系数尽可能小。在实际计算中，发现二阶耗散系数k(2)＝0、四阶耗散系数k(4)＝0.125的取值能够较好地控制耗散水平，又能得到稳定的计算结果。粘性通量项的离散采用二阶中心格式。时间离散采用A－F 近似因子化隐式格式，非定常计算过程采用双时间推进法进行[12]。 2.2 湍流模型
本文采用非定常RANS计算(URANS)与分离涡模拟(DES)以及DES的改进模型DDES互相对照。这三种方法的模型方程都是S-A模型的v方程：
式中的变量定义为：
其中
。模型常数为：
URANS使用的就是原始的SA模型，只是有显式的时间导数项，并且其解是随时间变化的非定常解，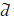
=d就是到粘性固壁的距离。对DES来说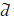，为由壁面距离和当地网格尺度共同确定的DES长度尺度[13]：
这样就为v的毁灭项分母上的长度尺度设置了一个限制，使其不能大于当地网格三个方向中的最大步长。这样，距壁面较远时，v的毁灭速度加快，大大降低了涡粘性，使小尺度旋涡结构得以发展。但是，DES对网格生成的要求很苛刻，当雷诺数很高的时候，网格的加密不当，以及RANS/LES交界面的位置不当，会导致速度型偏离对数率，甚至非物理的分 离现象[14]。为此，Spalart等[15]提出了一种改进的DES模型，称为延迟分离涡模拟(Delayed DES，DDES)。在DDES中，式(5)中r的计算公式改为
根据rd新定义了一个过渡函数： 而DES长度尺度重新定义为： DDES能够保证在平均剪切率高时，既便网格较细也不会进入LES模式。这样能够避免提前进入LES所致的雷诺应力不足，以及因此引起的提前分离。 3 计算结果及分析
根据Spalart[16]提出的准则，计算采用无量纲时间步长Δt=0.002D/U1。在流动达到统计稳态，即气动力系数开始有稳定幅度振荡后，再计算40个无量纲时间，以进行统计平均。计算在国家超级计算天津中心的天河一号集群进行，使用96个进程。计算达到稳态耗时6h，计算40个无量纲时间所用时间：URANS为40h，DES为42h，DDES为40.7h。DDES所用时间比DES略短，可能因为DDES在附着流动区保持RANS特性，而DES在部分区域出现了提前分离，导致收敛性变差。 3.1 时间平均流场
图 4-7展示了计算得到的表面流线与试验油流图的比较。如果不考虑试验所用油的物理特性、重力效应等因素，油流图与时间平均的表面流线图应该有相似的流动形态。图 4表明在前后轮的侧面，三种方法均得到了附着流动，这与试验得到的油流图是一致的。这说明在附着流动区域，URANS、DES和DDES都能够对流场作出正确的刻画。
 |
| 图 4 流线图，视角为从外侧前方。从左到右依次为：试验、URANS、DES、DDES Fig. 4 Streamlines,outboard view from front |
图 5为仰视图。可见前轮的流动方向是沿曲线由轮架流向轮侧面。仅在前轮的右下角(如图 5(a)中以S标出的白色区域)有一个小的分离区。此结果与图 5(b)中URANS和图 5(d)中DDES得到的流线图相似。相反，DES在约为前轮直径2/3的位置发生了提前分离(图 5(c))。对后轮而言，由于完全处于前轮的尾流之中，计算处于LES模式，DES与DDES都得到了与试验观测很符合的流动现象，而URANS得到的分离区过小。这说明DDES兼具有URANS在附着区和DES在分离区的优势。
 |
| 图 5 流线图，仰视：(a) 试验;(b) URANS; (c) DES; (d) DDES Fig. 5 Streamlines,looking up from under the wing side |
图 6显示了绕矩形截面轮架的大分离流动。在下方，各方法得到的流动图像基本一致，也与油流图 一致。进一步的观察显示DES在下游得到的分离线 位置比URANS更接近油流图，而DDES又好于DES。此外在上方，URANS得到的流线也与试验不一致，而DES和DDES得到的分离线更符合试验结果。这是因为锋利边缘导致的大分离流动没有贴体边界层，因而更适于DES计算。
 |
| 图 6 支架侧面的流线图。从左到右依次为：试验、URANS、DES、DDES Fig. 6 Oil flow visualization and streamlines,side view of truck |
图 7为从轮架向外观测的图像，流动图像的主要差别在后轮。URANS在后轮上方没有得到油流图中的分离线。对于更下游的位置，因为试验所用的轮轴是圆形截面，而计算中是正方形截面，所以不能区分结果的好坏。
 |
| 图 7 流线图，轮内侧：(a) 试验;(b) URANS; (c) DES; (d) DDES Fig. 7 Oil flow visualization and streamlines,in board view of wheels |
对计算和试验所得压力系数更定量的比较，可见图 8给出的沿轮对称面(z=0.4263D)周向的压力系数值，其中面向来流的位置为0°，背对来流为180°。图 8(a)和(b)显示无论是机翼一侧还是地面一侧，三种模型在前轮周向区域直到120°都得到了相似的结果。虽然各曲线的形状都类似，不同模型导致的提前和延迟分离还是造成了Cp行为的不同。URANS在前轮下游得到的Cp是三种模型中最低的，这是因为URANS的雷诺应力最大。这一特点在地面一侧使分离延迟(见图 5)，并造成150°处的Cp过低；而在机翼一侧，则促进轮架分离流动的再附，使Cp预测较为准确。而后轮由于完全处于前轮的尾流之中，URANS的分离不足造成地面一侧40°附近和机翼一侧80°附近的峰值没有捕捉到，而DES与DDES都得到了与试验观测很符合的流动现象。在后轮机翼一侧下游，DES没有捕捉到轮架分离流动的再附，造成Cp过高，而URANS和DDES都得到了较好的结果。这再次说明DDES兼具有URANS在附着区和DES在分离区的优势。
 |
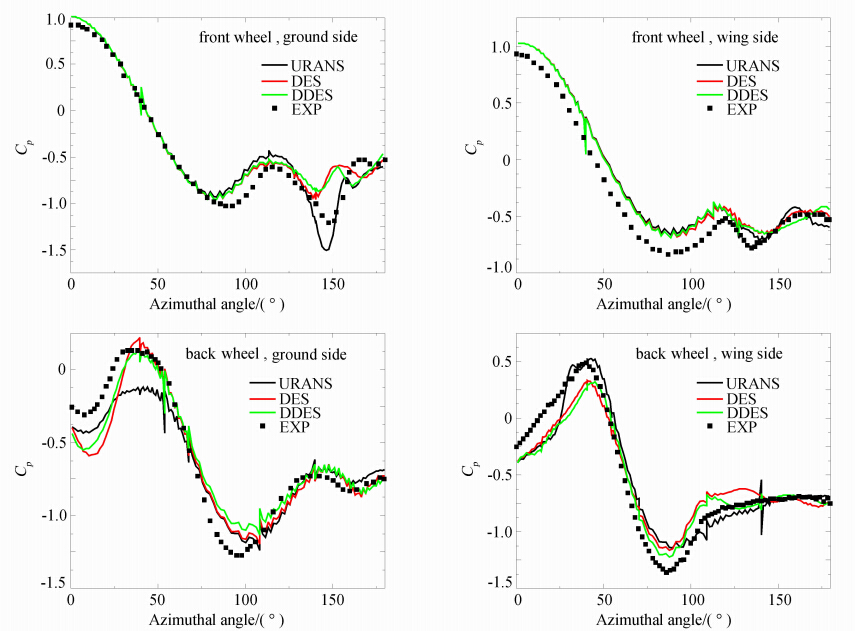| 图 8 周向压力系数分布，z=0.4263D Fig. 8 Cp along the circumference of wheels,z=0.4263D |
图 9展示了轮上的声压级(SPL)分布。前轮前半部分处于DES和试验的附着区，声压级的值较低。从前轮下游开始，声压级有所升高，这说明流动在前轮有类似转捩的过程。URANS在整个前轮得到的声压级都很低，说明URANS对非定常流动的捕捉能力不好。从前轮脱落的剪切流动撞击到后轮上，产生较高的SPL值。这在试验和计算中都有反映。但是，URANS得到的SPL在向下游传播的过程中迅速衰减，仅在脱落流动直接撞击的位置有较高的SPL值。这说明URANS的涡粘性过大，对流场小尺度结构耗散过快。DES和DDES都得到了较符合试验的结果，DDES的结果略好于DES。
 |
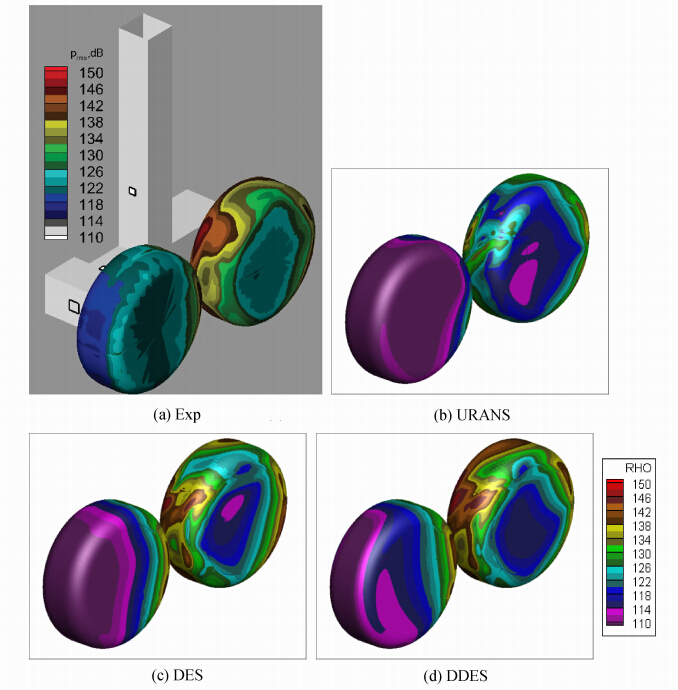| 图 9 表面声压密度：(a) 试验;(b) URANS; (c) DES; (d) DDES Fig. 9 Sound Pressure Level (SPL),outboard view |
图 10展示了基本起落架外形上的7个位置，三个在轮上，四个在轮架上。图 11和12是这些位置上试验和DDES计算得到的声压谱密度比较。在轮架 上的分离流动中，DDES得到的声压谱与试验结果较为相似，因为在锋利边缘分离流动中，流动处于LES模式。轮上几个位置的结果之间差别较大，因为此处压力脉动的预测对近壁网格分辨率的要求较高。后轮背风面(点1)处的声压级高估比较严重，可能是因为后轮下游处大分离区的范围较远，延伸到了网格分辨率较低的外区。Krajnovic＇等[17]也得到了类似的结果。此外，DDES高估了低频(St≤1)的压力振荡，这可能是因为统计样本不足导致误差较大。总体来说，对高频声压谱的预测比较准确。
 |
| 图 11 采样点声压谱 Fig. 11 SPL in points on the surface of RLG in Fig. 10 |
 |
| 图 12 采样点声压谱 Fig. 12 SPL in points on the surface of RLG in Fig. 10 |
用基于Spalart-Allmaras 湍流模型的URANS、DES和DDES方法对基本起落架流动进行了非定常数值模拟，并将其时间平均结果和表面声压结果与试验结果进行了对比分析。计算显示，非定常RANS在附着流动区能够得到合理的结果，但不能准确刻画分离流动的流动形态。DES和DDES都得到的时均表面流线、压力系数分布和表面声压分布都与实验符合很好，而DDES又好于DES，为更好的研究起落架噪声的抑制措施提供了一定的依据。
本文的结果显示DES和DDES能够处理基本起落架外形的复杂流动。比起非定常RANS而言，这两种方法都很好地刻画了流动的气动特性和声压特性，这是因为DES和DDES在流动发生分离后能够有效地降低涡粘性，促进小尺度湍流结构的发展。三种方法所用的时间成本大致相当，因此在同样的网格下，应该尽可能选取DES或DDES代替URANS进行非定常流场计算。文中使用中心格式得到了很稳定的计算结果，说明DES和DDES具有很好的鲁棒性。由于中心格式本身具有低耗散的优点，有望直接应用于声场的计算。进一步的工作包括加密计算网格以进一步改善表面压力和声压级的预测，并考察DES和DDES对网格的依赖性；用直接计算与声比拟的方法计算远场声压，并将二者的结果进行比较；对噪声声源进行准确定位，并提出优化准则等等。
致谢: 此项工作是在国家超级计算天津中心的“天河一号”超级计算机上完成的，感谢“天河一号”的大力支持。
| [1] | 龙双丽, 聂宏. 大型民机起落架噪声分析[J]. 航空科学技术, 2010(2): 16-18. |
| [2] | 龙双丽, 聂宏, 薛彩军, 等. 飞机起落架气动噪声特性仿真与试验[J]. 航空学报, 2012, 33(6): 1002-1013. |
| [3] | 张卫民, 郝璇, 陈大斌, 等. 大型客机气动噪声预测[J]. 航空制造技术, 2010, 14: 58-61. |
| [4] | Long S L, Nie H, Xu X. Aeroacoustic study on a simplified nose landing gear[J]. Applied Mechanics and Materials, 2012, 18: 184-185. |
| [5] | Xiao Z X, Liu J, Luo K Y, et al. Investigation of flows around a rudimentary landing gear with advanced detached-eddy-simulation approaches[J]. AIAA Journal, 2013, 51(1): 107-125. |
| [6] | Travin A K, Shur M L, Spalart P R, et al. Improvement of delayed detached-eddy simulation for LES with wall modelling[C]//Wesseling P, O[AKn-D]ate E, Priaux J, eds. European Conference on Computational Fluid Dynamics. The Netherlands: TU Delft, 2006. |
| [7] | Proceedings (CDROM) of the AIAA-NASA Workshop on Benchmark Problems for Airframe Noise Computations-I (BANC-1)[C]. Stockholm, Sweden, June 0-11, 2010. |
| [8] | Ventkatakrishnam L, Karthikeyan N, Meija K. Experimental studies on a rudimentary four wheel landing gear[R]. AIAA 2011-354. |
| [9] | Spalart P R. Introduction to 4 wheel rudimentary landing gear experimental-numerical project[R]. 2009. |
| [10] | 张玉东, 张卫民. 二维多段翼绕流流场数值模拟方法研究[C]//2009航空学会年会暨纪念冯如诞辰100周年会议, 2009. |
| [11] | Spalart P R. Detached-eddy simulation[J]. Annual Review of Fluid Dynamics, 2009, 41: 181-202. |
| [12] | 宋文萍, 杨永, 乔志德. 用双时间推进法求解非定常N-S方程的有关问题讨论[J]. 西北工业大学学报, 2000, 18(3): 99-103. |
| [13] | Spalart P R, Jou W H, Strelets M, et al. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach[C]//Advances in DNS/LES, 1997. |
| [14] | 徐晶磊, 阎超. 一个一方程Scale-Adaptive Simulation模型[C]//第十四届全国计算流体力学会议, 2009. |
| [15] | Spalart P R, Deck S, Shur M L, et al. A new version of detached-eddy simulation, resistant to ambiguous grid densities[J]. Theor. Comput. Fluid Dyn, 2006, 20: 181-195. |
| [16] | Spalart P R. Young person's guide to detached-eddy simulation grids[R]. NASA contractor report NASA/CR-2001-211032, 2001. |
| [17] | Krajnović S, Lárusson R, Helgason E, et al. PANS of rudimentary landing gear[C]//6th AIAA Theoretical Fluid Mechanics Conference, Honolulu, Hawaii: 27-30 June 2011. |