随着悬索桥跨径增大、结构趋于轻柔,其抗风性能成为了研究热点。吊索作为悬索桥的主要传力构件,它的安全直接关系着桥梁结构的安全。国内外已建的多座悬索桥发现塔周长吊索易发生振动,但振动机理并不清楚,通常采用增设阻尼器的方法抑制振动。
涡激振动是因气流绕经结构表面时产生了有规律的旋涡脱落而引起的结构振动[1]。巴西Rio-Niterói桥[2]和丹麦Great Belt East桥[3]的主梁均出现了明显地涡激共振。悬索桥塔柱断面通常较为钝化,且尺寸较大,桥塔尾流中易产生较强烈的旋涡。塔周长吊索处于桥塔尾流之中,桥塔尾流的作用易使塔周长吊索发生振动。对于离桥塔较近的吊索而言,桥塔尾流对其产生的气动干扰不容忽视。
圆柱的涡激振动是国内外研究的热点,徐枫[4]通过流固耦合方法对圆柱、圆柱群、表面带振荡附属物的单圆柱涡激振动进行了详细研究。陈文礼[5]采用数值模拟观察到了圆柱涡激振动的锁定和拍的现象。Pan Z Y[6]引入SST k-w湍流模型计算了低质量阻尼圆柱的涡激振动。Williamson[7]采用试验方法研究了两自由度低质量圆柱的涡激振动。此外,秦伟[8]建立一种新的预报并列双圆柱涡激振动响应的经验性模型。邓见[9]用分块耦合方法数值模拟了垂直交叉双圆柱绕流。然而,具体针对悬索桥吊索的抗风性能、疲劳寿命以及减振措施的研究则较为有限。杨靓[10]对悬索桥吊索风致抖振的疲劳可靠度进行了计算。朱保兵[11]等对带减振架吊索振动的主动控制进行了研究。已有研究通常是针对单一吊索进行的,考虑桥塔尾流对塔周长吊索振动性能影响的研究国内外未见报道,塔周长吊索常见振动的发生机理目前国内外尚无统一认识。
本文以实际工程为背景,首先分析了桥塔塔柱及吊索自身的旋涡脱落特性。在验证分析方法可靠性的基础上,进一步分析了桥塔尾流对同侧和对侧吊索产生的气动干扰,分别讨论了风速、风向角的影响,研究了桥塔尾流作用下塔周长吊索发生涡振的可能性。研究成果对实际工程设计及运营管理具有一定指导意义。 1 分析方法 1.1 工程概况
某大跨悬索桥成桥状态主缆线型如图 1所示。考虑到远离桥塔的吊索自振频率较高且受桥塔尾流的影响较弱,故选择离桥塔最近的三根吊索进行分析。取第二根吊索1/2高度处对应的截面作为计算截面,如图 2所示。桥塔的外轮廓为带圆角的方柱截面,吊索的外轮廓为圆截面,具体的尺寸大小及间距如图 2所示。
 |
| 图 1 结构立面布置图 Fig. 1 Elevation of structures |
 |
| 图 2 截面尺寸示意图(单位:mm) Fig. 2 Schematic diagram of cross-section size (unit: mm) |
桥塔及塔周吊索的长度较大,故将流场的计算近 似简化为平面问题,即计算其断面的二维绕流。模型尺寸采用实际尺寸,以确保模型与实际的雷诺数Re相等。考虑到截面分布的对称性以及计算工作量,首先对单个塔柱截面及对应一侧的三根吊索进行计算。当风向角较大时,一侧塔柱形成的尾流可能会影响另一侧的吊索,故进一步对大风向角下双塔柱截面及对应的六根吊索进行计算。
计算区域为长方形,如图 3所示。为满足阻塞率要求,当来流风向0°≤α<45°时(风向角α定义如图 2所示),取L1=7b,L2=30b,D1=D2=15b;当来流风向45°≤α≤90°时,取L1=9b,L2=13b,D1=7b,D2=30b。迎风侧边界设置为速度入口边界;背风侧边界设置为压力出口边界;上下边界视来流风向而定;塔柱及吊索表面设置为光滑壁面。
 |
| 图 3 计算区域 Fig. 3 Calculating region |
网格划分采用放射性结构化网格形式,贴近壁面的网格足够小,远离壁面的网格逐渐放大,这样既保证了结果精度又兼顾了计算成本,如图 4所示。
 |
| 图 4 局部网格划分 Fig. 4 Local grid partition |
气动力系数是描述静力风荷载的一组无量纲参数,体轴坐标系下气动力系数按式(1)~(3)定义。
式中,α为来流风攻角,对桥塔、吊索等竖直杆件而言即为风向角;FH(α)、FV(α)、MT(α)分别为风向角为α时截面受到的阻力、升力和扭矩;ρ为空气密度取1.225kg/m3;U为来流风速;H为迎风向宽度,即桥梁断面高度;B为顺风向宽度,即桥梁断面宽度;L为竖向长度,因研究对象为截面,取L=1。旋涡脱落频率与来流风速U及结构的截面形状有关,可用Strouhal数St来描述,按式(4)定义。
式中,f为旋涡脱落频率;D为物体垂直于来流方向平面上的特征尺寸。 2 吊索和塔柱自身的气动特性 2.1 吊索自振频率首先,引入无量纲参数ξ,按式(5)定义:
式中,T为吊索张力;EI为吊索弯曲刚度;l为索长。相关研究[12]表明,当ξ 较大时,吊索的动力特性和其对应弦的动力特性十分接近,边界条件对吊索自振频率的影响较小,可忽略边界条件的影响按两端铰支计算吊索的自振频率。再者,考虑到本文的侧重点在于分析吊索的气动特性,自振频率的大小仅提供一个参考。故本文通过ANSYS按两端铰支近似计算吊索的自振频率。
吊索的相关参数及ANSYS计算结果见表 1。其中,质量只考虑了镀锌钢丝而忽略了PE防护层。
| 吊索编号 | 1、4号 | 2、5号 | 3、6号 |
| 张力T/kN | 1277.447 | 1056.746 | 1108.821 |
| 质量m/(kg·m-1) | 39.519 | 22.711 | 22.711 |
| 索长l/m | 82.249 | 77.296 | 72.505 |
| 一阶频率 | 1.093 | 1.395 | 1.524 |
| 二阶频率 | 2.186 | 2.790 | 3.048 |
| 三阶频率 | 3.279 | 4.186 | 4.571 |
| 四阶频率 | 4.372 | 5.582 | 6.095 |
由表 1的计算结果可知,离桥塔越近的吊索的自振频率越低,发生风致振动的可能性越高。 2.2 吊索截面气动特性
以离桥塔最近的吊索1为对象,圆截面直径为0.105m,来流风速取14.3m/s,此时对应的Re=105,以便结果对比。根据前述方法计算了截面阻力系数CH的平均值,阻力系数CH和升力系数CL的变化频率。升力系数CL的变化频率反应了截面的旋涡脱落频率,代入式(4)可得对应的St。计算结果如表 2所示。
由表 2的计算结果可知,当Re=105时,本文计算的阻力系数CH的平均值以及St与已有文献的结果相符。因为旋涡的交替脱落,造成了阻力系数CH的变化频率为升力系数CL变化频率的两倍,以上均验证了本文模拟方法的准确性。
将吊索自振频率及St代入式(4)可计算涡激共振风速。吊索1的旋涡脱落频率较高,其前四阶模态频率对应的最高涡激共振风速为2.4m/s,此时风速较低,能量有限,且较紊乱。若不受其他构件气动绕流的干扰,吊索应不会由于自身的旋涡脱落而发生涡激共振。 2.3 桥塔截面气动特性
以塔柱1为对象,宽b=7.045m,高h=5m,圆角半径R=0.7m,来流风速取30m/s。根据前述方法进行计算,得到塔柱截面的阻力系数CH=1.248,旋涡脱落频率f=1.463Hz。
根据《公路桥梁抗风设计规范》[15],带圆弧角的矩形截面的阻力系数为:
CH= 1.7×max[(1-1.5r/b),0.5]=1.7×0.79=1.343
式中,1.7为宽高比3/2的矩形截面对应的阻力系数,本文塔柱的宽高比接近3/2。通过以上比较可知,本文计算得到的阻力系数稍小于规范值,但考虑到规范取值较为保守,说明本文模拟塔柱的结果具有一定的可信度。
另外,桥塔的旋涡脱落频率接近吊索的一阶自振频率,吊索很可能在桥塔尾流的干扰下发生振动。 3 塔柱尾流致同侧吊索涡振
以塔柱1及同侧吊索1~3为研究对象,分析不同来流风速和风向角时,桥塔尾流对同侧吊索气动特性造成的影响。 3.1 风向角的影响
取来流风速U=30m/s,风向角范围-10°~30°,通过非定常分析可以得到吊索阻力系数和升力系数的时程曲线,对时程曲线进行频谱分析,可以得到对应的功率谱,并提取最大幅值对应的卓越频率,如表 3所示。
| 风向角 | -10° | -5° | 0° | 5° | 10° | 20° | 30° |
|
塔柱1的旋涡 脱落频率 | 1.412 | 1.414 | 1.483 | 1.451 | 1.389 | 1.376 | 0.937 |
|
吊索1阻力和升力 系数的变化频率 | 1.412 | 1.414 | 1.483 | 1.451 | 1.389 | 1.376 | —— |
|
吊索2阻力和升力 系数的变化频率 | 1.412 | 1.414 | 1.483 | 1.451 | 1.389 | —— | —— |
|
吊索3阻力和升力 系数的变化频率 | 1.412 | 1.414 | 1.483 | 1.451 | 1.389 | —— | —— |
|
注:1吊索阻力系数和升力系数的变化频率相等。 2 “——”表示吊索阻力系数和升力系数的卓越频率大于50Hz。 | |||||||
由表 3可知,对于塔柱截面,当风向角为0°时,塔柱1的旋涡脱落频率与单塔柱的旋涡脱落频率相近,而且吊索面积远不足塔柱面积的0.1%,故在后续分析中忽略吊索对塔柱气动特性的影响。对于吊索截面,当风向角为-10°~10°时,三根吊索阻力系数和升力系数的变化频率都等于塔柱的旋涡脱落频率。当风向角增大至30°时,三根吊索阻力系数和升力系数的变化频率已不再等于塔柱的旋涡脱落频率了。 3.2 来流风速的影响
分别取来流风速U=10m/s、20m/s、30m/s,并考虑0°、5°、10°的风向角,采用相同的方法计算吊索截面阻力系数和升力系数的变化频率,结果如图 5所示。其中,因为吊索阻力系数和升力系数的变化频率都等于塔柱的旋涡脱落频率,所以图 5代表了三根吊索中任意一根吊索的阻力系数和升力系数的变化频率。
 |
| 图 5 不同风速下吊索阻力系数和升力系数的变化频率 Fig. 5 Frequencies of drag and lift coefficient of suspenders at different wind velocities |
因为吊索气动力系数的变化频率等于塔柱的旋涡脱落频率,所以图 5本质上是塔柱旋涡脱落频率随风速及风向角的变化关系。由图 5可知,风速增大使桥塔的旋涡脱落频率增大,从而使吊索气动力系数的变化频率也增大,其关系近似为线性关系。风向角的改变(0°≤α≤10°)对气动力系数的变化频率影响不大。 3.3 吊索振动分析
由前述的分析可知,当塔柱截面的形状及来流风向角一定时,塔柱的旋涡脱落频率与风速近似呈线性关系,即St不变。吊索气动力系数的变化频率等于塔柱的旋涡脱落频率,也与风速近似呈线性关系。根据表 3的结果和吊索一阶频率可以推算不同风向角下吊索可能发生涡激共振的风速,结果如表 4所示。
| 风向角 | 吊索1/(m·s-1) | 吊索2/(m·s-1) | 吊索3/(m·s-1) |
| -10° | 23.22 | 29.64 | 32.38 |
| -5° | 23.19 | 29.60 | 32.33 |
| 0° | 22.11 | 28.22 | 30.83 |
| 5° | 22.60 | 28.84 | 31.51 |
| 10° | 23.61 | 30.13 | 32.92 |
| 平均值 | 22.95 | 29.29 | 31.99 |
由表 4可知,当风向角为-10°~10°时,吊索的发振风速与其自振频率有关,离桥塔最近的吊索1自振频率低,平均发振风速只有22.95m/s;而离桥塔越远的吊索,平均发振风速逐渐增高。 3.4 桥塔尾流分析
为分析桥塔尾流对吊索气动力系数造成的影响,以吊索2为研究对象,图 6为塔柱1和吊索2在0°和10°风向角时的气动力系数时程曲线。
 |
| 图 6 塔柱1及吊索2的气动力系数时程曲线 Fig. 6 Time-history curve of aerodynamic coefficient of No.1 tower column and No.2 suspender |
当风向角为0°时,吊索2的阻力系数和升力系数时程曲线与塔柱的升力系数时程曲线非常相似。塔柱脱落的旋涡几乎完全抑制了吊索自身的旋涡脱落,从而控制了吊索的气动特性,迫使吊索的阻力系数和升力系数变化频率等于塔柱的旋涡脱落频率,而不再是单圆柱截面时的两倍关系了。
当风向角为10°时,吊索逐渐偏离塔柱的尾流区域。某些时刻,塔柱尾流已不能抑制吊索自身的旋涡脱落了,而吊索自身的旋涡脱落频率高于塔柱的旋涡脱落频率,所以吊索的气动力系数时程曲线出现了黑色高频率成分。取塔柱旋涡脱落的一个周期T进行分析,如图 6所示。在(t-1/4T)时刻至(t+1/4T)时刻内,吊索气动力系数时程曲线与塔柱升力系数时程曲线很相似;但在(t+1/4T)时刻至(t+3/4T)时刻内,吊索自身出现了旋涡脱落,即时程曲线中的黑色高频率成分。进一步分析,图 7为风向角为10°时,t时刻至(t+T)时刻内,流场的涡量图。由图 7可知,正风向角时,塔柱下侧脱落的涡1离上侧脱落的涡2相隔较近,在(t-1/4T)时刻至(t+1/4T)时刻内抑制了吊索自身的旋涡脱离;塔柱上侧脱落的涡2离下侧脱落的涡3相隔较远,当涡2离开后,吊索自身出现了旋涡脱落,使气动力系数出现波动且幅度逐渐增大;但随着涡3来到,波动幅度开始减弱,而后吊索自身的旋涡脱落又被涡3所抑制。
 |
| 图 7 10°风向角下流场各时刻的涡量图 Fig. 7 The vorticity at different times of flow field under 10° wind direction |
当风向角为30°时,吊索已离开了塔柱的尾流区域,塔柱尾流已不能再抑制吊索自身的旋涡脱落了。此时,吊索截面的气动特性主要由自身的旋涡脱落决定。但是桥塔的存在仍会使吊索周围的流场发生周期性的变化,一方面可能对吊索气动力系数的幅值造成影响,另一方面风速的改变使吊索的旋涡脱落频率不是一个确定的值,而是在一定的范围内变化。 4 塔柱尾流致对侧吊索涡振
随着风向角增大,塔柱对同侧吊索的影响逐渐降低,但却可能影响对侧吊索,故以塔柱1、2和吊索1~6为研究对象进行分析。
取风速U=30m/s,风向角30°~90°进行计算。考虑到大风向角时,两塔柱的相互干扰以及塔柱四周的圆角会使流场变得非常复杂。为便于后续分析,故 仅以升力系数为例,对其时程曲线进行频谱分析,提取最大幅值对应的卓越频率,结果如表 5所示。
由表 5可知,当风向角为30°~70°时,部分吊索的气动特性受塔柱尾流控制,其升力系数变化频率等于塔柱旋涡脱落频率。随着风向角增大,吊索依次脱离塔柱尾流的控制。当风向角为80°~90°时,吊索升力系数功率谱图中已无桥塔尾流引起的低频成分了,该区域内吊索应不会发生共振。
| 风向角 | 塔柱2/Hz | 塔柱1/Hz | 吊索4/Hz | 吊索5/Hz | 吊索6/Hz | 吊索1/Hz | 吊索2/Hz | 吊索3/Hz |
| 30° | 0.906 | 0.906 | 0.906 | 0.906 | 0.906 | 0.906 | 0.906 | 0.906 |
| 45° | 0.953 | 0.550 | 0.953 | 0.953 | —— | 0.953 | 0.953 | 0.953 |
| 60° | 0.716 | 0.716 | 0.716 | —— | —— | 0.716 | 0.716 | —— |
| 70° | 0.711 | 0.711 | —— | —— | —— | 0.711 | —— | —— |
| 80° | 1.002 | 1.002 | —— | —— | —— | —— | —— | —— |
| 90° | 1.037 | 1.037 | —— | —— | —— | —— | —— | —— |
| 注: “——”表示吊索阻力系数和升力系数的卓越频率大于50Hz。 | ||||||||
对于吊索1、2、3,在塔致同侧吊索涡振的分析中,当风向角为30°时,三根吊索气动力系数的变化频率已不等于塔柱1的旋涡脱落频率。但当考虑了塔柱2时,这三根吊索的升力系数功率谱图中又再次出现了塔柱尾流引起的低频成分了。说明两塔柱的相互干扰使吊索受影响的范围增大了。
为进一步分析吊索的气动特性,以风向角60°为例,塔柱和吊索的升力系数时程曲线如图 8所示,对应的功率谱如图 9所示。
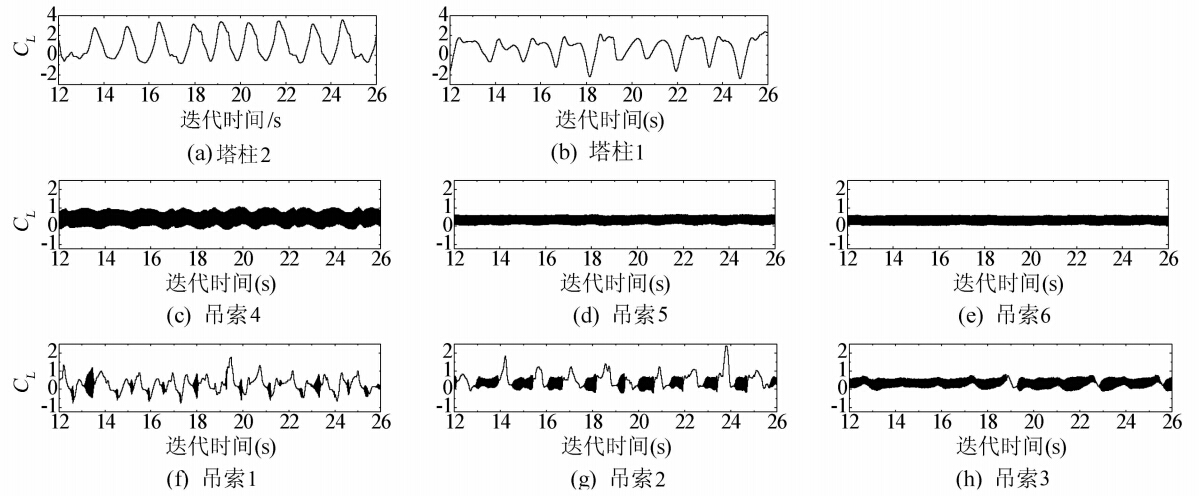 |
| 图 8 升力系数时程曲线 Fig. 8 Time-history curve of lift coefficient |
 |
| 图 9 升力系数功率谱 Fig. 9 Power spectrum of lift coefficient |
由图 8可知,吊索4、5、6全程可见黑色高频成分,说明塔柱尾流不能抑制其自身的旋涡脱落,吊索升力系数功率谱中的低频成分是由于塔柱尾流影响了升力系数幅值而产生的。吊索1、2的旋涡脱落仍然在多数时间内被塔柱尾流所抑制。仍按塔柱尾流致同侧吊索涡振的方法来推算吊索的发振风速,那么六根吊索可能的发振风速最小为34.4m/s,大于-10°~10°风向角范围内吊索的发振风速。这是由于大风向角下,塔柱的旋涡脱落频率有所降低。
但是,由图 9可以看到另一个现象,塔柱的升力系数功率谱中,存在两个幅值较大的卓越频率,它们分别为1.357Hz和1.499Hz。同时,在吊索1的升力系数功率谱中出现了1.499Hz的卓越频率;在吊索2的升力系数功率谱中出现了1.357Hz的卓越频率。这是由于大风向角下,塔柱复杂的气动特性所引起的。在风向角为45°和70°时也存在这样的现象,如表 6所示,而且这些频率对应的幅值均很大。
| 风向角 | 塔柱1,2/Hz | 吊索1/Hz | 吊索2/Hz | 吊索3/Hz | |
| 45° | 1.225 | 1.908 | —— | 1.908 | —— |
| 60° | 1.357 | 1.499 | 1.499 | 1.357 | —— |
| 70° | 1.264 | 1.422 | 1.264 | —— | —— |
由表 6知,这些较大幅值对应的卓越频率接近甚至大于吊索的一阶自振频率,使吊索1、2在22m/s的来流风速下就存在发生涡激共振的可能性。
综上所述,当风向角为30°~70°时,一方面由于塔柱尾流影响另一侧吊索;另一方面,两塔柱相互之间的气动干扰进一步增大了其尾流的影响范围,当风向角较大时,多根吊索在22m/s的风速下仍然存在发生共振的可能。 5 结 论
本文采用CFD方法分析了桥塔尾流对塔周长吊索涡振性能的影响,可得出以下结论:
(1) 塔周长吊索自身的旋涡脱落频率较高,而自振频率较低。对于离桥塔最近的吊索,其前四阶模态频率对应的最高涡激共振风速约为2.4m/s,此时风速较低,能量有限,且较紊乱,若不受其他构件气动绕流的干扰,吊索应不会由于自身的旋涡脱落而发生涡激共振。
(2) 当风向角为-10°~10°时(来流风向为顺桥向时风向角为0°),吊索气动特性决定于同侧塔柱的尾流,其脉动气动力的卓越频率等于塔柱的旋涡脱落频率,且该频率接近吊索的一阶频率。当风速介于23m/s~32m/s时,吊索可能发生涡激共振,且离塔柱越近的吊索,涡激力越强,发振风速越低,可能的振幅也越大。
(3) 当风向角为±10°~±70°时(来流风向与桥轴向垂直时风向角为90°),塔柱尾流将影响同侧甚至另一侧的吊索,两塔柱相互之间的气动干扰进一步加大了塔柱尾流的影响范围。距塔柱较近的两对索的脉动气动力受塔柱尾流影响明显,在22m/s的风速下就存在发生涡激共振的可能性。距塔柱较远的一对索受塔柱尾流的影响则较为有限。
| [1] | Zhu Ledong. The qualitu of system simulation and amplitude correction method of bridge vortex-induced resonance section model tests[J]. Engineering Mechanics, 2005, 22(5): 204-208. (in Chinese) 朱乐东. 桥梁涡激共振试验节段模型质量系统模拟与振幅修正方法[J]. 工程力学, 2005, 22(5): 204-208. |
| [2] | Battista R C, Pfeil M S. Reduction of vortex-induced oscillations of Rio-Niterói bridge by dynamic control devices[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 84(3): 273-288. |
| [3] | Frandsen J B. Simultaneous pressures and accelerations measured full-scale on the Great Belt East Suspension Bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89: 95-129. |
| [4] | Xu Feng. Numerical simulation of fluid-solid coupling vibration and flow control of structures[D]. Harbin: Harbin Institute of Technology, 2009. (in Chinese) 徐枫. 结构流固耦合振动与流动控制的数值模拟[D]. 哈尔滨: 哈尔滨工业大学, 2009. |
| [5] | Chen Wenli, Li Hui. CFD numerical simulation of vortex-induced vibration of a circular cylinder based on a RANS method[J]. Journal of Xi'an University of Architecture and Technology(Natural Science Edition), 2006, 38(4): 509-513. (in Chinese) 陈文礼, 李惠. 基于RANS的圆柱风致涡激振动的CFD数值模拟[J]. 西安建筑科技大学学报(自然科学版). 2006, 38(4): 509-513. |
| [6] | Pan Z Y, Cui W C, Miao Q M. Numerical simulation of vortex-induced vibration of a circular cylinder at low mass- damping using RANS code[J]. Journal of Fluids and Structures, 2007, 23: 23-37. |
| [7] | Williamson C H K, Jauvtis N. A high-amplitude 2T mode of vortex-induced vibration for a light body in XY motion[J]. European Journal of Mechanics B/Fluids, 2004, 23: 107-114. |
| [8] | Qin Wei, Kang Zhuang, Sun Liping, et al. Research on vortex-induced vibration of two side-by-side cylinders by using an emprical model[J]. The Qcean Engineering, 2013, 31(2): 11-18. (in Chinese) 秦伟, 康庄, 孙丽萍, 等. 并列双圆柱涡激振动的经验性模型研究[J]. 海洋工程. 2013, 31(2): 11-18. |
| [9] | Deng Jian, Ren Anlum, Zou Jianfeng. Numerical simulations of flow around two circular cylinders in cruciform arrangement and vortx structures analysis[J]. Acta Aerodynamica Sinica, 2005, 23(1): 29-34. (in Chinese) 邓见, 任安禄, 邹建锋. 垂直交叉双圆柱绕流数值模拟及涡结构分析[J]. 空气动力学学报, 2005, 23(1): 29-34. |
| [10] | Yang Liang. Research on time-varying reliab- ility of suspension bridge hanger in a whole-life period[D]. Changsha: Hunan University, 2009. (in Chinese) 杨靓. 悬索桥吊索寿命期内动态可靠性分析[D]. 长沙: 湖南大学, 2009. |
| [11] | 朱保兵, 李国强. 带减振架吊索振动的主动控制研究[C]//第五届全国现代结构工程学术研讨会论文集. 广州: 第五届全国现代结构工程学术研讨会, 2005. |
| [12] | Xu Xiafei, Ren Weixin. Effect of boundary conditions on the estimation of suspender tension[J]. Journal of Railway Science and Engineering. 2008, 5(6): 26-31. (in Chinese) 徐霞飞, 任伟新. 边界条件对吊索索力估算的影响[J]. 铁道科学与工程学报. 2008, 5(6): 26-31. |
| [13] | Schlichting H. Theory of boundary layer[M]. Translated by Xu Yanhou. Beijing: Science Press, 1988. (in Chinese) 史里希廷 H. 边界层理论(上册)[M]. 徐燕侯译. 北京: 科学出版社, 1988. |
| [14] | Bi Jihong, Yu Huajun, Ren Hongpeng. Two dimensional numerical simulation of flow over a static square cylinder and a static circular cylinder[J]. Journal of China Three Gorges University(Natural Sciences), 2012, 34(1): 41-45. (in Chinese) 毕继红, 余化军, 任洪鹏. 静止方柱和圆柱绕流的二维数值分析[J]. 三峡大学学报(自然科学版), 2012, 34(1): 41-45. |
| [15] | JTG/T D60-01-2004 Wind-resistent design specification for highway bridges[S]. Beijing: Standards Press of China, 2009. (in Chinese). |





