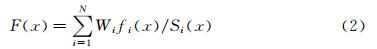0 引 言
先进的气动布局设计是各类高超声速飞行器总体技术性能指标设计的关键所在,各国对此非常重视,并利用各种研究手段对其展开大量的研究。如美国航天飞机的布局设计,先后经历了三个阶段,设计了几百个外形,最终选定现在的外形。目前各国的高超声速飞行器气动布局都以发展高升阻比、升力式再入复杂外形为特点,如乘波体、升力体、组合升力体和翼身组合体等。但升力体布局形式最主要的问题在于还不能较好地解决升阻比和防热性能与操稳特性之间的矛盾。
HTV-2是美国研制的一种无动力高超声速滑翔飞行器。在气动布局上,采用了带乘波体特征的高升阻比翼身融合体。按照设计要求,HTV-2将具有极高的升阻比,远远高于航天飞机,高升阻比使得弹道下降段航程更长,同时横向机动范围更大[1]。两次失败的飞行试验表明,在气动布局、操稳性能等方面的问题依然存在。
NASA的OSP(Orbital Space Plane)计划指出为使再入飞行器具有较小的再入过载和较大的机动能力,要求飞行器高超声速和亚声速升阻比都要大;为了降低着陆速度,要求亚声速升力系数较大等。该计划提出的融合升力体气动布局(Blended Lifting Body,BLB)试图在传统的翼/身外形的气动效率与纯升力体高容量效率之间寻求平衡,有望适应再入飞行器的各种要求[2, 3]。
James S. Greathouse 和Benjamin S. Kirk等人研究对比分析了返回舱外形、细长体、升力体以及有翼飞行器等各种外形的飞行器气动力、热性能,详述了NASA选型参数指标。并运用牛顿流理论,应用简单而准确的SNEWT程序进行了快速计算与比较分析。文献中详述了包括Overflow、CART3D、LAURA、Configuration Based Aerodynamics (CBAERO)等CFD代码的特点和适用流动情况,并给出部分算例,在飞行器气动外形优化设计的选型及计算方面给出参考[4, 5]。
随着我国航天技术的不断发展,对各种飞行器的气动性能提出了越来越高的要求,高超声速飞行器的布局设计也越来越迫切。国内的多学科设计优化(MDO)理论研究尚处于起步阶段,但MDO应用于设计研究的工作已经在各领域展开。国防科大的王振国等人在其专著中对多学科设计优化理论进行了详细论述研究,举例说明了多学科设计优化理论在飞行器设计中的应用[6]。西工大的江志国等人发展了自己的针对高超声速飞行器气动布局的优化软件,总结出一套适用于高超声速飞行器的性能指标计算模型、优化算法模型和优化思想,可应用于高超声速飞行器的概念研究及初步设计[7]。车竞等人将Pareto非劣解和遗传算法结合起来,克服标准遗传算法的缺点。为了提高优化效率,引入模拟退火算法进行局部搜索,形成了混合的模拟退火遗传算法,并有效地用于高超声速飞行器总体性能优化研究中[8]。唐伟、夏露等人也在高超声速飞行器优化设计研究方面做出了大量的研究工作[9, 10]。
由于国内尚未开展BLB概念的布局设计研究,本文拟参考美国BLB概念设计的经验与方法及俄罗斯Clipper飞行器外形,通过对融合升力体布局形式和参数影响规律的研究,开展跨速域高升阻比融合升力体(BLB)气动布局设计与优化,发展新型跨速域高升阻比再入飞行器。主要通过应用快速高效的优化设计平台,计算分析特征尺寸对流场特性及飞行器气动性能的影响,优化设计候选布局,并建立外形设计与优化的方法。这对未来发展高超声速再入飞行器及相关气动布局研究具有十分重要的意义。
1 研究方法
1.1 研究方法简介
总体研究思路是基于优化平台集成三维建模、网格自动化及气动力快速计算模块,形成优化设计方法。首先通过三维建模软件作图得到基本气动布局外形并完成参数化建模,通过基于笛卡尔网格和Euler方程的流场快速求解方法计算气动力系数,基于优化平台选择优化算法完成气动布局优化设计,并针对优化得到的典型布局完成综合气动分析。
1.2 流场求解方法
在气动布局优化设计中,快速准确地获得气动力特性非常重要。这是因为优化设计过程中的目标函数选取为升阻比等气动特性,而这些气动特性取决于飞行器的气动布局和构形,并且与外型尺寸的关系无法用明确的函数表达出来。这就需要发展一种快速而准确的得到气动力特性的方法,以满足优化设计的精度和效率要求。
本文计算基于可压缩Euler方程,采用有限体积法离散,计算网格使用直角笛卡尔网格,流动变量位于网格中心,时间离散采用Runge-Kutta法,通过时间推进得到稳态解,空间离散为迎风格式,选择使用min mod限制器,格式具有TVD性质,采用多重网格法加速迭代过程。程序运行结束后输出可读气动力系数文件[11]。
算例验证显示,该方法计算精度高,在高超声速流动及亚跨声速流动的数值计算中都有出色表现,可用于多种飞行器气动力的计算分析。该方法的主要特点是计算速度快,效率较高[12]。数值计算中,网格量在130万时,单机运行的计算时间可控制在10min之内。在优化设计时,在保证计算精度的前提下,适当减少网格量,可将单状态运算时间控制在5min以内,能够大幅缩短设计周期,降低计算成本。
1.3 参数化方法介绍
由于在优化设计过程中需要随时生成更新的数模和网格,人工操作已经不能满足计算要求。这就需要我们完成气动外形的参数化,即发展一种能够快速生成光滑的数模文件的方法。并且网格生成应该高度自动化,以便于提高计算效率,缩短优化周期。本文通过一个VB语言的脚本文件驱动外形特征变量的方法完成外形的参数化生成,并输出parasolid格式的数模文件。在新外形生成时,驱动文件有错误参数的正确处理功能,如出现负值时,该文件并不会中断程序,而是在输出原始外形后继续优化过程。所以,在出现错误尺寸时该文件不会导致优化过程中断,也不会影响到优化结果,具有很好的鲁棒性[11]。
2 优化算法验证计算
2.1 优化算法简介
数值优化算法有快速高效、精度高的特点,但处理多峰值问题易陷于局部最优解,适用于单峰值优化问题。其基本思想就是迭代法,首先给出目标函数(设为f(x))的极值点的一个初始估计x(1)(称为初始点),然后计算一系列的点x(2),x(3),x(4),……,希望该点列{x(k)}的极限值就是目标函数的极值点。公式表达为:
本文选用直接数值优化技术中的修正可行方向算法MMFD(Modified Method of Feasible Directions)。该方法针对约束优化问题可以通过梯度搜索快速得到优化解,约束可以是等式或者不等式,在获得最优解时可以以很高的精度满足约束条件。MMFD遍寻当前设计点周围区域,首先确定使得目标函数下降的搜索可行方向,沿着可行方向搜索;进行一维优化搜索,求得最优步长并确保下一步的优化点位于可行域内。在可行域内部搜索时,使用共轭梯度法确定搜索方向;在可行域边界(即存在起作用约束时),搜索方向应与起作用约束面成直角或者钝角,即[gm(xk)]Tsk≤0。可行方向的确定方法是按梯度法搜索前进,这在不连续的优化空间里是难以实现的。
在优化过程中,为了避免陷入局部最优,在目标函数可能为多峰值时,需要采用全局优化算法。多目标优化设计中选用可以生成pareto解集的多目标优化算法——邻域培植遗传算法NCGA (Neighborhood Cultivation Genetic Algorithm)。在多目标优化设计中一般不存在多个目标同时达到最小的绝对最优解,不同目标之间的优化是相互冲突的,这就需要找到一个折衷的解集,在这个解集里不存在任何一个解可以在一个目标更加优化的同时而保证其他目标不变坏,这个解集即是pareto最优解,该解集中的解均为所设计问题的“非劣解”。领域培植遗传算法是一种可以自动生成pareto最优解的遗传算法,该算法可以通过调节遗传操作参数控制优化过程,最终输出pareto最优解和按给定目标权值得到的最优解[13]。
在多目标优化中得到的pareto最优解是一个由多个非劣解组成的解集,本文根据加权组合法从中选择符合设计要求的最优解。加权组合法是将各自分目标函数fi(x)按照重要性分配权系数Wi(Weight)及比例因子Si(scalefactor),然后求和构成总的统一目标函数F(x),即:
为验证上述集成方法的有效性,通过对印度的RLV(Reusable Launch Vehicles)返回舱展开优化设计,并将优化结果与文献数据对比,验证其在双目标优化设计中的应用[14]。RLV返回舱选择球双锥外形,外形轮廓及优化计算模型如下:
优化目标:min As,max Xcp
约束条件:V≥3m3
设计变量:
选择NCGA与MMFD相结合的优化算法进行优化[14],NCGA选择群体大小30,进化代数25,交叉概率0.9,变异概率0.01。而文献中同样采用遗传算法优化,其群体大小30,进化代数500,交叉概率0.9,变异概率0.001。优化结果对比如表 1所示,外形如图 2。
对比显示,该方法能够在满足约束条件的情况下获得比文献中所列的优化结果更加优化的外形,即压心位置更大,表面积和体积更小,达到了保证稳定性并且降低发射质量的优化目的,可以应用于飞行器气动布局的多目标优化设计。
本文结果更优的原因在于遗传算法的参数设置及数值优化算法的应用上。文献[14]设置变异概率偏小,优化过程中遍寻设计空间,效率低,导致遗传算法的优势没有发挥出来。另外,数值优化算法MMFD的应用也更进一步的优化了遗传算法得到的最优解。
3 新型气动布局优化设计
3.1 新型气动布局设计及参数化
前期调研表明,俄罗斯Clipper飞船返回舱具有较高升阻比,在防热性能及稳定性等方面也有较好表现[15, 16]。参考Clipper外形,设计了新型融合升力体外形,外形及轮廓线如图 3所示。
该布局由三部分组成,分别是上部旋成体、中部弧-台及下部弧面。
我们约定:图中上部轮廓线各点标注为P1-P4,下部母线弧上的对应点,则相应标记为P11-P44,以示关联,相对应的两点横坐标相等。以P1点为例,坐标表示为(XP1,YP1),依此类推。圆心坐标的下标以该圆的半径表示,以下部母线大圆为例,其半径为Rd,故圆心坐标表示为(XRd,YRd)。外形总长记为Length。原始外形的特征尺寸参数如表 2所示。
以下表述各点及各特征尺寸间的几何关系。
首先,Rn、L1、θ1、R1、L2、θ2、Rd、D为自变量。鉴于在后续计算中常用到各点坐标,故先推导图中各点的坐标表示公式,如表 3。
其中底部大圆圆心坐标(XRd,YRd)可以由下式推导得出:
以上所述,将外形轮廓线中所有特征尺寸表达出来,由8个自变量决定。
接下来介绍旋转及放样特征相关的几何特征尺寸。如图 3所示,沿轴向分别在P2、P3、P4点取3个截面,编号为草图 2~草图 4。由于特征尺寸编号较多,为防止混淆,我们约定,尺寸下标只有一个数字的表示草图编号,如D4代表草图 4所在的基准面到顶点的距离;尺寸下标两个数字的,则第一个数字代表草图编号,第二个数字为在本草图内的编号,如R41代表草图 3中的标记为第1个的圆半径;下标为数字和字母组合的,数字代表草图编号,字母L代表左,R代表右(相对于左视图方向),如R42R代表草图 4中右侧第2个圆半径。
其中,沿轴向的三个截面轮廓相似,由6个圆弧组成,如上图 4所示。这里以草图 4为例加以说明。草图 4中,自变量参数包括: θ41、R43、R44、θ44,应变量为R41、R42。其中R41=YP4,R42由几个自变量共同决定。草图 3中,θ31、R33、R34与草图 4中相应特征尺寸相等,即草图 3中只增加了 θ34一个自变量。同样,草图 2中只增加了θ24一个自变量。这样,由6个自变量参数可以完全描述沿轴向的三个截面。
综上,该布局可以由14个自变量特征参数完全描述。
3.2 新型气动布局优化计算
如前文所述,外形轮廓部分可由8个自变量参数描述,横截面部分可由6个自变量参数完全描述。其中θ41、R43、R44为三个横截面的共有参数,θ24、θ34、θ44为各截面自有参数。
作为初步优化设计,优化过程中保持基本轮廓形式不变,三个截面共有参数不变,即保持该布局顶部圆柱部分、过度圆弧半径及底部大圆半径不变,设计变量为θ24,θ34,θ44,在参数化外形合理并且保证能够生成有效外形的范围内约束设计变量变化范围,并构建了基于原始外形的优化设计模型,优化目标为高超声速高升阻比及进场亚声速高升力系数最大化。优化模型可表示如下,其中的角度单位为弧度:
优化目标:max (L/D)hyper,CL sub
设计变量:
选用NCGA和MMFD相结合的混合优化算法,计算马赫数分别取为:Mahyper=5.0,Masub=0.5,迎角均为10°。通过迭代优化计算,得到的优化外形如图 5所示。
本文完成了在马赫数5.0和0.5情况下的多状态气动力计算分析,如图 6所示。
可以看到,该优化布局的高超声速和亚声速升阻比都比较高,迎角为0°时升阻比在1.0~1.3左右,并且随着迎角的增加急速升高,在迎角8°~9°之间分别达到最大值,随后随着迎角的增加而降低。高超声速最大升阻比约为2.14,亚声速最大升阻比约2.95。
亚声速升力系数较大,并且随着迎角的增加而升高。迎角为0°时,亚声速升力系数约为0.57,并且随着迎角的增加而升高。在升阻比最大的8°迎角时,升力系数约为2.70。
由此可见,该优化布局在高超声速再入及低速进场阶段具有良好气动特性,与Clipper原始外形[12]相比,同样具有更好的升阻特性,是一种能够初步满足再入要求,值得深入研究的新型气动布局。
在该例中,应用个人计算机运算完成了全部优化设计工作,节约了大量计算机时,降低了计算成本。
基于上述研究,通过新型融合升力体的气动布局设计与优化,并对典型优化结果展开气动特性计算分析,得到以下结论:
(1) 设计的新型融合升力体气动布局能够初步满足全速域高升阻比及进场亚声速高升力系数的设计要求。优化设计结果较初始外形更“宽、扁”,在进一步的优化研究中应考虑容积率的影响,保证飞行器实用性。
(2) 本文建立的气动布局快速优化设计方法计算速度快,成本低,能够应用于复杂外形飞行器的优化设计工作。
存在的不足之处主要表现在优化过程中没有考虑气动热及操稳性能等方面的影响,变量约束还应再考虑容积率的影响。
下一步的工作将重点解决上述问题,进而考虑综合气动力、气动热、弹道及静、动稳定性等方面,开展全面综合的多约束多目标多变量的复杂外形优化设计工作。

Rn/m θ1 θ2 L1/m L2/m As/m2 Xcp/m V/m3
优化结果 0.8786 24.98° 34.08° 0.4664 0.3112 8.37 1.272 3.0079
文献数据 0.735 22.13° 31.87° 0.288 0.871 10.45 1.213 4.0719 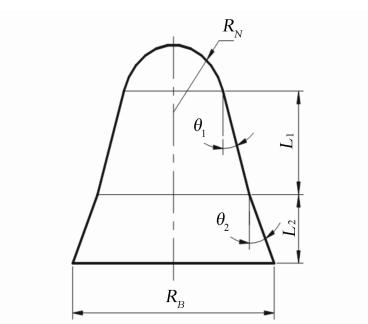
图 1 印度RLV返回舱轮廓图Fig. 1 Contour line of RLV reentry capsule 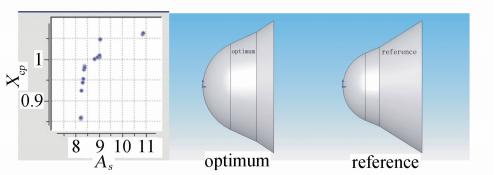
图 2 印度RLV优化pareto解集及外形比较Fig. 2 Pareto plot and the optimization
contour of RLV reentry capsule 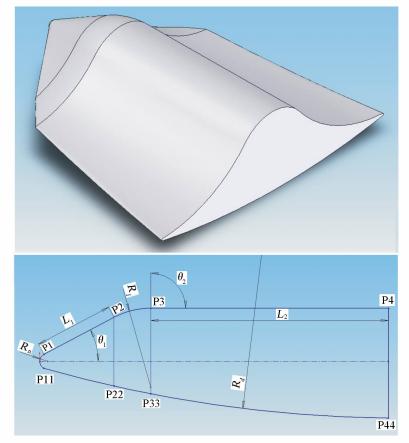
图 3 新布局外形及轮廓Fig. 3 New fashioned shape and contour
特征尺寸名称 特征尺寸符号
球头半径 Rn
第一锥长度 L1
过渡圆半径 R1
第二锥长度 L3
尾底中部下垂增量 D
下部母线弧半径 Rd
第一锥角 θ1
第二锥角 θ2
特征点 X坐标 Y坐标
P1 XP1=Rn(1-sinθ1) YP1=Rncosθ1
P2 XP2=XP1+L1cosθ1 YP2=YP1+L1sinθ1
R1 XR1=XP2+R1sinθ1 YR1=YP2-R1cosθ1
P3 XP3=XR1-R1sin(π/2-θ2)
YP3=YR1+R1cos(π/2-θ2)
P4 XP4=XP3+L2cos(π/2-θ2)
YP4=YP3+L2sin(π/2-θ2)
P11 XP11=XP1 YP11=-YP1
P22 XP22=XP2
YP22=YRd-R2d-XRd-XP2220.5
P33 XP33=XP3
YP33=YRd-R2d-XRd-XP3320.5
P44 XP44=XP4 YP44=-YP4-Δ 

图 4 截面轮廓图Fig. 4 Contour line of section 

图 5 优化结果示意图Fig. 5 Schematic drawing of optimization result 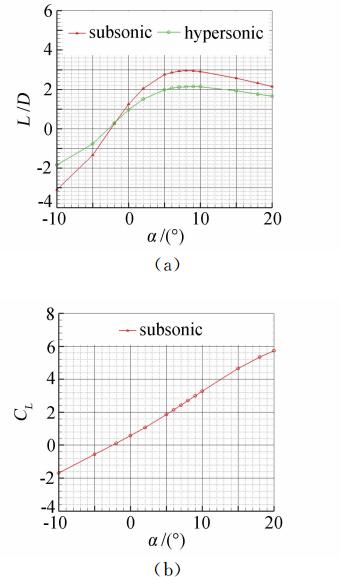
图 6 优化布局气动力特性Fig. 6 Aerodynamic characteristics of optimization shape
| [1] | Henri D Fuhrmann. A blended lifting body aerodynamic design for the orbital space plane[R]. AIAA 2003-3807. |
| [2] | Douglas Nelson. Reentry performance analysis of an orbital space plane concept[J]. AIAA 2003-7018. |
| [3] | 彭彪, 张志峰, 马岑睿, 等. 国外高超声速武器研究概述及展望[J]. 飞航导弹, 2011, 5: 20-25. |
| [4] | Benjamin M Andersen. Aerodynamic control on a lunar return capsule using trim-flaps[R]. AIAA 2007-855. |
| [5] | James S Greathouse, Benjamin S K, Randolph P L. Crew Exploration Vehicle (CEV) crew module shape selection analysis and CEV aeroscience project overview[R]. AIAA 2007-603. |
| [6] | 王振国, 陈小前, 罗文彩, 等. 飞行器多学科设计优化理论和应用研究[M]. 北京: 国防工业出版社, 2006, 04. |
| [7] | 江志国, 唐硕, 车竞. 高超声速巡航飞行器气动布局优化软件设计[J]. 飞行力学, 2008, 26(1): 52-55. |
| [8] | 车竞, 唐硕, 何开锋. 高超声速飞行器气动布局总体性能优化设计研究[J]. 空气动力学学报, 2009, 27(2): 214-219. |
| [9] | 唐伟, 高晓成, 李为吉, 等. 双椭圆截面再入飞行器的气动计算及布局优化设计[J]. 空气动力学学报, 2004, 22(2): 171-174. |
| [10] | 夏露, 高正红, 李天. 飞行器外形多目标多学科综合优化设计方法研究[J]. 空气动力学学报, 2003, 23(1): 275-280. |
| [11] | 李治宇. 载人登月返回舱气动布局概念设计与优化方法研究[D]. [硕士学位论文]. 绵阳: 中国空气动力研究与发展中心, 2011.06. |
| [12] | 李治宇, 袁先旭, 杨彦广, 等. 基于笛卡尔网格的无粘气动力计算[C]//第十五届全国计算流体力学会议, 2012.08. |
| [13] | 周明, 孙树栋. 遗传算法原理及其应用[M]. 北京: 国防工业出版社, 1999.06. |
| [14] | Rajesh Kumar Arora. Aerodynamic shape optimization of a reentry capsule[R]. AIAA 2003-5394. |
| [15] | Pavel Vashchenkov, Andrey Krylov. Numerical analysis of high altitude aerodynamic of reentry vehicles[C]//13th International Space Planes and Hypersonic Systems and Technology. AIAA 2005-3409. |
| [16] | Mikhail S I, et al. Numerical modeling of high altitude aerodynamic of reentry vehicles[C]//9th AIAA/ASME Joint Thermophysics and Heat Transfer Conference. AIAA 2006-3801. |
| [17] | Alex Van der Velden, et al. iSIGHT-FD, a Tool for multi-objective data analysis[R]. AIAA 2008-5988. |