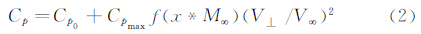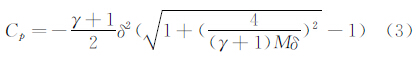0 引 言
高超声速飞行器在大气层中飞行时所经历的气动环境十分复杂,且会产生强烈的气动加热现象。而气动加热造成的结构温升可能造成飞行器热变形甚至破坏,从而带来安全隐患。准确预测结构温度场在高超声速飞行器热防护系统与结构设计中显得尤为重要。
高超声速飞行器经历的气动加热过程是一个持续、非定常过程,不可避免地会涉及到与结构温度场/应变场的耦合作用。如忽略多物理场的耦合效应将会给结构温度场和应力/应变场预测带来偏差。气动热与传热的耦合问题经长期研究与发展,不管是耦合方法研究还是实际工程应用都已开展了大量工作。美国自20世纪60年代至今,已基本形成了“气动加热/温度场/应力场”一体化分析能力[1],并对X-43等飞行器开展气动加热/热响应的耦合分析[2, 3]。国内的一些学者也开展了一些气动加热/温度场耦合方面的研究。桂业伟[4]对外流场计算采用N-S方程,结构温度场分析采用差分法进行了耦合方法研究。黄唐[5]对流场采用TVD格式的有限差分法,对温度场采用有限元法进行杂交的松耦合计算。任青梅[6]以商用软件为基础开发了耦合分析平台用于飞行器设计。另一方面,也有大量学者对温度场变化造成飞行器结构固有特性变化和动气动弹性特性变化问题进行研究。Harry[8]早在1965年就开展了非线性温度分布简支板在超声速流中的颤振特性研究,研究表明非均匀温升造成的结构应力对平板颤振特性的影响是明显的。James[9]对温度呈曲线分布的三角翼静热气动弹性问题进行了研究,John[10]则对其热气动弹性稳定性和操控性进行了研究。国内的相关问题研究则主要集中在南航、北航、西工大、国防科大等几个高校和相关科研院所[11, 12, 13, 14]。夏巍[11] 等采用气动力活塞理论以及准定常热应力理论建立了考虑热效应的复合材料壁板颤振的气动弹性力学模型。叶献辉[12] 等采用类似的方法对三维壁板的热颤振问题进 行了计算分析。张伟伟[13] 等将多种气动力工程方法用于高超声速机翼颤振计算模拟中,并比较了不同方法的气动弹性计算结果。吴志刚[14] 等同样应用VanDyke活塞理论计算了翼面热颤振问题。
根据现有文献资料,在气动热/传热耦合研究中,尚未考虑结构变形对耦合特性的影响。在热气动弹性特性研究方面,也多是以假设的温度分布或不考虑变形的气动加热结果为研究基础。而在实际飞行过程中,特别是长时间飞行后,结构变形对温度场的影响往往是不能忽略的,对气动力/热环境也都有直接的影响,这方面的工作鲜有报道。本文以飞行器静态热气动弹性计算方法[15]为基础,对高超声速飞行器机翼模型进行了考虑热气动弹性变形影响的气动热与传热耦合计算,并与不考虑变形对热环境影响情况的计算结果进行了对比分析。 1 计算方法与实现 1.1 热气动弹性问题计算流程
热气动弹性问题是一个典型的多学科问题,一次性完全求解这样的多学科耦合问题非常复杂,其涉及的气动力、气动热、惯性力和弹性力间存在复杂的强弱耦合关系,如图 1所示[16]。
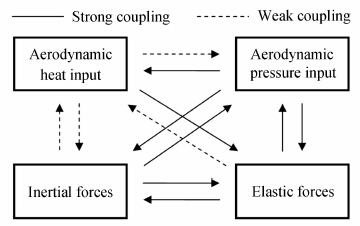 |
| 图 1 热气动弹性问题耦合关系Fig. 1 Coupling diagram of aerothermoelastic problem |
本文以文献[15]建立的静态热气动弹性问题计算流程为基础,进行每一个时刻的热气动弹性计算,在时间推进过程中计入气动弹性变形对气动热的影响,即每一时刻的气动热计算都采用当前时刻弹性变形后的外形进行计算,再带入结构传热计算,获得下一时刻的结构温度场。
图 2为考虑变形对气动热影响的静热气动弹性问题计算流程图。其中的虚线部分表示在每一个时刻静热气动弹性计算完毕后,根据该时刻的弹性变形情况进行气动热计算,从而在时间上累计弹性变形对结构温度场的影响。
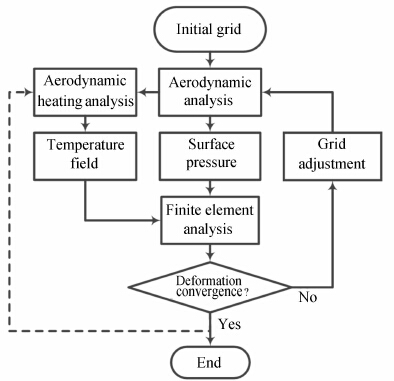 |
| 图 2 考虑变形对气动热影响的静热气动弹性问题计算流程图Fig. 2 Flowchart of the computation of static aeroelastic problem with deformation effects considered |
对于有迎角飞行器气动加热,本文采用了跟踪流线法来计算[17]。跟踪流线法主要思想是利用轴对称比拟概念,在弹体上布满流线,利用小横向流假设沿每根流线按等价的轴对称体处理,将三维边界层问题简化为流线坐标下的轴对称问题,层流热流用修正的Lees公式或工程方法计算,湍流热流用经过形状因子和压缩因子修正的平板湍流参考焓方法,用工程方法近似计算激波形状。舵面迎风面热流是按钝前缘平板计算的,前缘驻点线的热流用修正的无限后掠圆柱理论计算,干扰区的热环境通常用试验数据拟合关联方法计算。
(2) 气动力计算方法
高超声速领域的工程计算方法发展较为完善。目前,国外已发表的超声速、高超声速工程计算方法有数种,如牛顿法、修正牛顿方法等[17]。
考虑本文验证模型特性,迎风区采用了考虑边界层修正和真空修正的内伏牛顿理论计算压力系数:
背风区则采用的普朗特-迈耶公式:
(3)三维温度场计算方法
对三维温度场计算采用有限体积法,时间方向采用显式的二阶TVD-Runge-Kutta方法。本文中考虑的对流加热边界热流为给定冷壁热流。需要进行热壁修正,修正公式如下:
其中:Hre为恢复焓,Hw为壁焓,H300为壁温为300K的焓值,qc为冷壁热流。(4)热应力场/位移场计算方法
对结构热应力场/位移场的计算是通过热弹性力学控制方程组完成的。该方程组由弹性力学的变分原理可将其化为经典的有限元求解方程:
其中,K是已知的结构整体刚度矩阵,P是已知的结构结构点载荷列阵,它们是由单元刚度矩阵和单元等效结点载荷列阵集合而成。a则是待求解的结构结点位移列阵。对物体受热产生的应力问题,物体由于热膨胀只产生线应变,而剪切应变为零。这种由于热变形产生的应变可以看作初应变ε0。ε0表达式是:
在这种情况下应力应变关系就可表示成:
其中,α是材料的热膨胀系数(1/℃),对各向异性复合材料来说,各方向的膨胀系数α通常是不相同的;φ0是结构的初始温度场;φ是结构的稳态或瞬态温度场。φ可由温度场分析得到的单元结点温度φi插值求得。 2 算例计算与分析 2.1 高超声速飞行器全动舵面模型图 3为计算所用高超声速飞行器全动舵面模型。图中翼根处有一轴承固定于飞行器身部,研究过程中忽略了轴承结构本身,仅在轴承根部施加位移约束。翼根长2.67m,翼展1.27m,前缘后掠角30°,材料为高温合金GH1015,结构初始温度300K。以高度20km,速度5马赫,迎角10°进行巡航飞行。
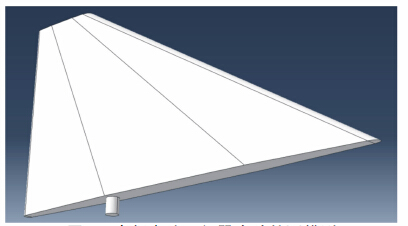 |
| 图 3 高超声速飞行器全动舵面模型Fig. 3 The whole moving rudder model of hypersonic vehcile |
在真实飞行器中,为降低飞行器质量,提高有效载荷,通常在不影响结构安全和飞行性能的情况下会使用空芯结构。本文假设的空芯机翼模型结构计算网格如下图 4所示,模型“蒙皮”厚度5mm。
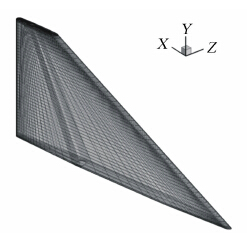 |
| 图 4 空芯机翼模型结构计算网格示意图Fig. 4 Computing grid diagram of hollow whole moving rudder model |
如图 5和图 6所示,分别为巡航飞行时不考虑弹性变形情况下的舵面热流云图和舵面展向不同位置沿轴线方向的热流曲线图。从图中可以看出,舵面前缘驻点热流最高,热流值约为1500kW/m2。舵面迎风区发生了转捩,且转捩后的湍流区热流值较层流区有显著提升,湍流区最大热流值接近300kW/m2。
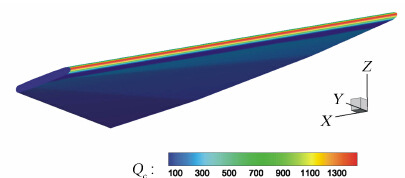 |
| 图 5 机翼模型热流云图Fig. 5 The heat fluxnephogram of whole moving rudder model |
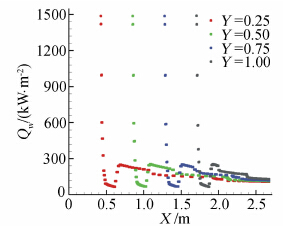 |
| 图 6 机翼模型沿轴线方向热流曲线图Fig. 6 The heat flux curve of whole moving rudder model along the axial direction |
为了更为精确的表征考虑热气动弹性影响的温度场变化,根据计算模型的外形特点,本文选取了三个表面监控点,如图 7所示,分别为前缘附近的点A,侧面位置的点B和后缘附近的点C,其具体坐标如表 1所示。
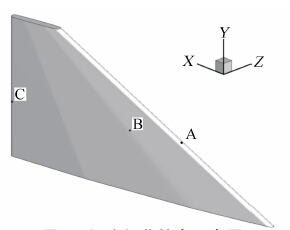 |
| 图 7 温度场监控点示意图Fig. 7 The monitoring points of temperature field |
| Monitoring points | Coordinate value |
| A | (0.855,0.5,-0.146) |
| B | (1.39,0.5,-0.3) |
| C | (2.65,0.5,-0.496) |
图 8为计算得到的巡航飞行500s时刻机翼结构的表面温度场云图。从图中可以看出,整个迎风面温度均超过了900K,接近于平衡状态。图 9所示的监控点温度值随时间变化曲线也能表明这一状态。此外,从曲线图中还可以看出,对于前缘驻点附近A点,在考虑变形对气动热的影响时,温度变化较为明显,由不考虑变形影响时的1164K下降到1137K,下降了27K。而监控点B和点C的温度变化则很小,且呈微幅上升趋势。迎风面上B点从992K上升到996K,上升了4K,而后缘附近的C点则从923K上升到925K,上升了2K。分析原因,主要是模型受气动力的影响产生了一定的弹性变形,使迎风角度(迎角)变得更大,改变了模型驻点位置,因而机翼原驻点位置A的温度有较为明显的下降。同时,迎风角度的变化使得迎风面上的B点和C点的气动加热都略微增大,造成了温度的微幅上升。总体而言,除前缘驻点附近,变形对气动热/结构温度场的影响还是较小的。但对于热防护结构来说,前缘驻点温度的准确预测是十分重要的,计算结果则恰恰说明了考虑弹性变形对结构温度场预测的重要性。
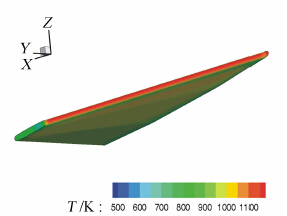 |
| 图 8 模型飞行500s后结构温度场云图Fig. 8 The nephogram of structure temperature field at 500s |
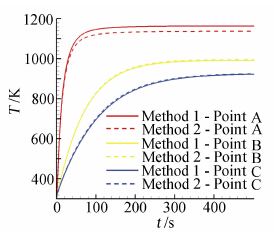 |
| 图 9 不同计算策略下模型监控点温度随时间变化图Fig. 9 The temperature versus time of the structural monitoring points |
本文以飞行器静态热气动弹性计算方法为基础,对高超声速飞行器机翼模型进行了考虑热气动弹性变形影响的气动热与传热耦合计算,并与不考虑变形对热环境影响情况的计算结果进行了对比分析。计算结果表明,虽然对于大面积区域结构变形对气动热/结构温度场的影响较小,但对于热防护结构重点关注且精度要求较高的前缘驻点区域,预测温升有明显改变,且最大温升位置也随变形而改变。由此,也说明了考虑弹性变形对结构温度场预测的重要性。该研究工作为进一步提高飞行器结构温度场预测精度及结构性能评估能力奠定了基础。
| [1] | Mcnamara J J, Friedmann P P, Powel K G, et al. Aeroelastic and aerothermoelastic vehicle behavior in hypersonic flow[R]. AIAA 2005-3305, 2005. |
| [2] | Ruth M A, John A D, Michael C L. Thermal analysis methods for an earth entry vehicle, National aeronautics and space administration[R]. Langley research center, 2000. |
| [3] | Blades E, Ruth M, Fuhrman D. Aeroelastic Analysis of the X-34 Launch Vehicle[R]. AIAA 1999-1352, 1999. |
| [4] | Gui Yewei, Yuan Xiangjiang. Numerical simulation on the coupling phenomena of aerodynamic heating with thermal response in the region of the leading edge[J]. Journal of Engineering Thermophysics, 2002, 23(6):733-735.(in Chinese) 桂业伟, 袁湘江. 类前缘防热层流场与热响应耦合计算研究[J]. 工程热物理学报, 2002, 23(6):733-735. |
| [5] | Huang Tang, Mao Guoliang, Jiang Guiqing, et al. Two dimensional coupled flow-thermal-structural numerical simulation[J]. Acta Aerodynamica Sinica, 2000, 18(1):115-119. (in Chinese) 黄唐, 毛国良, 姜贵庆, 等. 二维流场、热、结构一体化数值模拟[J]. 空气动力学学报, 2000, 18(1):115-119. [LL] |
| [6] | Ren Qingmei, Yang Zhibin, Cheng Zhu, et al. Development of the platform for analysis coupling aeroheating and structural temperature field[J]. Structure & Environment Engineering, 2009, 36(5): 33-38. (in Chinese) 任青梅, 杨志斌, 成竹, 等. 气动加热与结构温度场耦合分析平台研发技术[J]. 强度与环境, 2009, 36(5): 33-38. |
| [7] | Geng Xiangren, Zhang Hanxin, Shen Qin, et al. Study on an integrated algorithm for the flowfields of high speed vehicles and the heat transfer in solid structures[J]. Acta Aerodynamica Sinica, 2002, 20(4): 422-427.) 耿湘人, 张涵信, 沈清, 等. 高速飞行器流场和固体结构温度场一体化计算新方法的初步研究[J]. 空气动力学学报, 2002, 20(4): 422-427. |
| [8] | Harry G Schaeffer, Walter L Heard, Jr. Flutter of a simply supported panel subjected to a nonlinear temperature distribution and supersonic flow[R]. AIAA 65-112. |
| [9] | James R Batt, Richard H Gallagher. Nonlinear thermoelastic effects on hypersonic stability and control, part II, analytical and experimental static aerothermoelasticity[R]. Technical Documentary Report No. FDL-TDR-64-16. |
| [10] | John H Wykes, Robert E Lawrence. Aerothermoelasticity: its impact on stability and control of winged aerospace vehicles[J]. Journal of Aircraft, 1965, 2(6): 517-526. |
| [11] | Xia Wei, Yang Zhichun. Flutter analysis of composite panels with thermal effects[J]. Journal of Northwestern Polytechnical University, 2005, 23(2):180-183.(in Chinese) 夏巍, 杨智春. 复合材料壁板热颤振的有限元分析[J]. 西北工业大学学报, 2005, 23(2): 180-183. |
| [12] | Ye Xianhui, Yang Yiren. Thermal flutter analysis of a three-dimension panel[J]. Journal of Vibration and Shock, 2008, 27(6):55-59. (in Chinese) 叶献辉, 杨翊仁. 三维壁板颤振分析[J]. 振动与冲击, 2008, 27(6): 55-59. |
| [13] | Zhang Weiwei, Fan Zewen, Ye Zhengyin, et al. A better engineering method for computing aeroelastic characteristics of supersonic and hypersonic wings[J]. Journal of Northwestern Polytechnical University, 2003, 21(6):687-691.(in Chinese) 张伟伟, 樊则文, 叶正寅, 等. 超音速高超声速机翼的气动弹性计算方法[J]. 西北工业大学学报, 2003, 21(6): 687-691. |
| [14] | Wu Zhigang, Hui Junpeng, Yang Chao. Hypersonic aerothermoelastic analysis of wings[J]. Journal of Beijing University of Aeronautics and Astronautics, 2005,31(3):270-273.(in Chinese) 吴志刚, 惠俊鹏, 杨超. 高超声速下翼面的热颤振工程分析[J]. 北京航空航天大学学报, 2005, 31(3): 270-273. |
| [15] | Liu Lei, Gui Yewei, Geng Xiangren, et al. Study on static aerothermoelasticity for hypersonic vehicle[J]. Acta Aerodynamica Sinica, 2013, 31(5): 559-563.(in Chinese) 刘磊, 桂业伟, 耿湘人, 等. 高超声速飞行器热气弹静态问题研究[J]. 空气动力学学报, 2013, 31(5): 599-563. |
| [16] | Mcnamara J J, Friedmann P. Aeroelastic and aerothermoelastic analysis of hypersonic vehicles: current status and future trends[R]. AIAA 2007-2013, 2007. |
| [17] | Huang Zhicheng. Hypersonic aircraft aerodynamics[M]. Beijing: National Defence Industry Press, 1995.(in Chinese) 黄志澄. 高超声速飞行器空气动力学[M]. 北京: 国防工业出版社, 1995. |
| [18] | Mcnamara J J. Aeroelastic and aerothermoelastic behavior of two and three dimensional surfaces in hypersonic flow[D]. [Ph.D. thesis]. Ann Arbor: University of Michigan, 2005. |
| [19] | Liu Lei. Study on the characteristics and similarity criteria of aerothermoelasticity for hypersonic vehicle[D]. [Ph. D. Thesis]. Mianyang: China Aerodynamics Research and Development Center. 2014.(in Chinese)刘磊. 高超声速飞行器热气动弹性特性及相似准则研究[D]. [博士学位论文]. 绵阳: 中国空气动力研究与发展中心, 2014. |
| [20] | Biot M A. Influence of thermal stresses on the aeroelastic stability of supersonic wings[J]. Journal of the Aeronautical Sciences, 1957, 24: 418-420. |
| [21] | Thornton E, Dechaumphai P. Coupled flow, thermal, and structural analysis of aerodynamically heated panels[J]. Journal of Aircraft, 1988, 25(11):1052-1058. |
| [22] | Culler A J, Crowell A R, Mcnamara J J. Studies on fluid-structural coupling for aerothermoelasticity in hypersonic flow[R]. AIAA 2009-2364, 2009. |