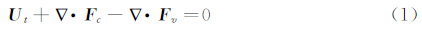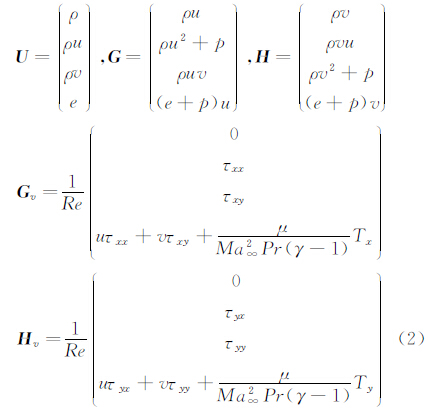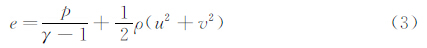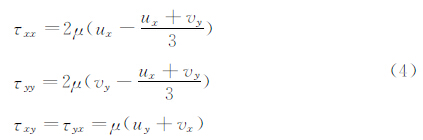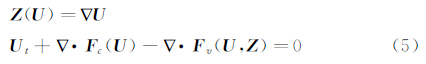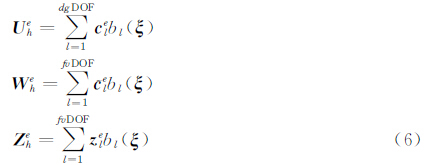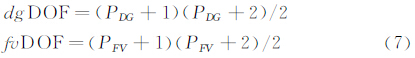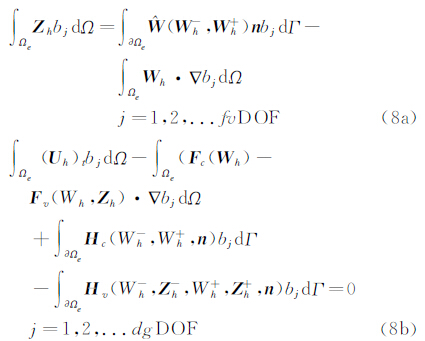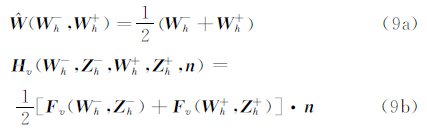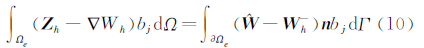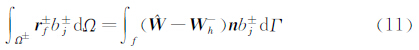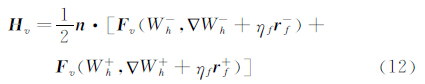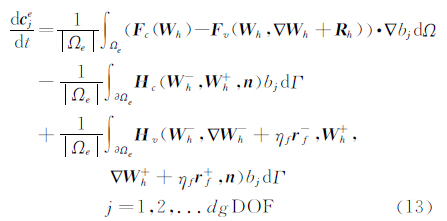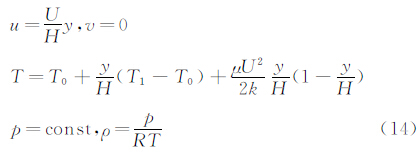2. 中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000
2. Computational Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China
0 引 言
近几十年来，随着计算流体力学(CFD)和计算机技术的发展，非结构/混合网格生成技术及其数值计算方法得到了飞速的发展。非结构网格具有适于复杂几何外形、方便网格自适应等突出优点，进一步发展的混合网格技术部分克服了非结构网格需要大量计算资源的不足，成为网格技术研究的热门话题。已知的大部分商业CFD软件使用二阶精度有限体积方法(FVM)，尽管其成功解决了大量的工程实际问题，但在CFD领域仍有一些问题需要高阶精度(三阶或以上精度)方法才能较好地解决。这主要是因为低阶精度(二阶或以下精度)方法具有较大的数值耗散与色散，对一些非常复杂的流动问题，如旋涡主导的流动、分离、湍流等问题，其通常难以给出精细的流场结构。一般认为对于湍流的大涡模拟(LES)、直接数值模拟(DNS)等问题，低阶方法固有的数值耗散可能大到掩盖这些真实的物理粘性，因此必须采用高阶方法；在计算气动声学、计算电磁学等领域，需要对长时间历程的波传播特性进行高精度的数值模拟，低阶方法在网格规模受计算机资源限制时往往无法准确模拟流场的特性，带来无法接受的计算结果，此时亦有必要使用高阶方法。另外，分析表明，对于误差水平要求不高的问题，一般低阶方法可以用较小的计算代价来解决；而当问题对误差水平的要求很高时，使用高阶方法计算代价更小，效率更高[1]。
近二十年来，基于非结构/混合网格的高阶精度计算方法发展迅速，出现了大量的计算方法，主要有k-exact有体积方法[2, 3]、间断Galerkin方法(DGM)[4, 5]、谱体积(SV)方法[6]、谱差分(SD)方法[7]、及将DG、SV、SD等方法统一在一个框架之内的CPR(Correction Procedure via Reconstruction)方法[8]等等。高阶FV方法和以DG方法为代表的DG/SV/SD/CPR等方法都各具优点，但仍有可以改进的空间。如高阶FV方法需要扩充模板来提高重构精度，在非结构网格下模板的搜寻扩展很不方便并且方法不紧致；DG方法的计算量和存储量非常大等等。由此构造结合FV方法和DG方法优点的混合方法是一种较好的选择，其已受到很多学者的关注，并提出了多种混合算法，其核心思想大多是使用本单元和相邻单元的多个自由度重构一个更高阶的分布，使用这个更高阶的分布来得到本单元的较低阶自由度信息的高阶更新。为了进一步增加DG方法计算精度而对其使用重构算子的思想最早由Cockburn等[9]提出，后来Ryan等[10]做了进一步的发展。然而他们只是在最后输出时刻使用重构算子，因而实际上是DG方法的后处理技术。Dumbser和Munz首次提出从DG方法计算开始时刻就使用线性重构算子，构造出一类重构的DG方法，命名为PNPM方法[11, 12]；基于类似思想，Luo等提出了RDG[13, 14](Reconstructed DG)方法，构造了三阶精度RDG(P1P2)格式；张来平等基于Taylor基函数构造出一类适用于混合网格的DG/FV混合方法[15, 16, 17]；在原始CPR格式的基础上，王志坚等借鉴PNPM方法和DG/FV混合方法的思想，构造了一系列PNPM-CPR格式[18, 19]。这几种混合方法均显示出了很好的性能，具有每个自由度比FV方法和DG方法更高效、方法紧致、隐式时间离散内存需求更低等很多优点。
张来平等在构造DG/FV混合方法[15, 16, 17]时，提出了“静态重构”和“动态重构”的概念，基于静动态“混合重构”的思想，构造了一类三阶以上精度的DG/FV混合格式，并应用于三角形/四边形混合网格下的标量方程和Euler方程的数值模拟。在该混合方法中，对每个目标单元构造其模板，并使用模板中每个单元上物理量已知的PDG阶多项式分布重构出目标单元上更高阶的PFV阶多项式分布(PFV>PDG，称为静态重构)；使用此高阶分布来计算数值通量和数值积分，从而对每个单元中物理量的PDG阶多项式分布系数使用常规的DG方法存储和时间推进(称为动态重构)，得到下一时刻的PDG阶分布系数。上述静态重构算法可以采用k-exact最小二乘重构[11, 12]、强插值重构[13, 14]、Gauss-Green公式重构[15, 16, 17]等方法。大量的数值算例表明该方法达到了设计精度，且比同阶DG方法具有更高的计算效率。
本文将此DG/FV混合方法推广于二维Navier-Stokes方程的数值模拟，将方法形式精度阶提高到4~5阶。使用BR2格式[20, 21]来计算粘性通量；使用层次的标准正交基函数和带约束最小二乘重构，这样静态重构算法简单且高效，并且在DG时间推进中(动态重构)无需求质量矩阵的逆矩阵，节省了计算资源。本文给出了几种精度阶的DG/FV格式和DG格式的计算量的定性理论分析和数值结果，表明相比同阶精度DG方法DG/FV混合方法计算量减少约40%。对有解析解的Couette流动问题计算表明，本文方法达到了设计精度；层流平板流动和定常、非定常圆柱绕流等经典算例结果表明，随着精度的提高，在较粗的计算网格上亦能得到高精度的计算结果。 1 计算方法 1.1 控制方程
在直角坐标系中，不计体积力和外加热的无量纲化守恒形式的Navier-Stokes方程组可以写为：
其中U为守恒变量；Fc=(G,H)，G、H分别为x、y方向上的无粘(对流)通量；Fv=(Gv,Hv)，Gv、Hv分别为x、y方向上的粘性通量。它们的具体形式为： 其中选取流场中某一特征长度L、来流速度u∞、密度ρ∞、温度T∞、粘性系数μ∞并引入普朗特数Pr进行无量纲化。(2)式中比热比γ=1.4，普朗特数Pr=0.72，μ为动力粘性系数，一般由Sutherland(萨泽兰特)半经验公式给出。单位体积流体总能量为： 粘性应力张量为： 1.2 DG/FV空间离散方法
引入辅助变量Z，将方程(1)重写为如下两个一阶方程：
将计算域Ω划分成互不重合的单元集合Ωh= {e}，令Ωe表示控制单元e。令解空间为VhPDG={(v)4:ve∈PolyPDG(e)∀e∈Ωh}，其中PDG为解分布多项式阶数，PolyPDG表示不超过PDG阶的多项式构成的线性空间；令重构空间为VhPFV，其中PFV≥PDG为重构多项式阶数，具体定义类似VhPDG。单元e中，变量Uh、重构变量Wh和辅助变量Zh分别可以写成如下的多项式展开形式：
其中cle、cle和zle是分布系数，bl(ξ)取参考单元内的正交基函数，ξ是参考单元的局部坐标，相应多项式的自由度数为：
下面我们寻求Uh∈VhPDG满足方程(5)的弱形式，由某种重构算法得到变量Wh∈VhPFV(具体参考[11, 12, 13, 14, 15, 16, 17, 18])，并令辅助变量Zh∈(VhPFV)2，将方程(5)乘以检验函数bj，然后在单元Ωe上使用分部积分方法，可得：
上式中为了消除Wh和矢量通量Fc、Fv在边界∂Ωe上的二义性，使用了数值通量、Hc、Hv。检验函数bj取单元e的基函数。Wh－、Wh+分别表示本单元和邻单元变量的高阶重构分布的值，Zh－、Zh+分别表示本单元和邻单元的辅助变量，n为单元e边界单位外法向。式(8)中无粘数值通量Hc可以使用常规的欧拉黎曼求解器得到[15, 16, 17]，本文使用Roe格式[22]。与粘性相关的数值通量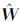
、Hv如何计算是DG/FV混合方法推广到N-S方程数值模拟上的核心内容。本文使用由BR1格式改进而得的BR2格式[20, 21]。BR1格式形式简单，如下：
由于BR1格式需要求解和存储辅助变量Zh，其计算量和存储量大，且BR1格式需要用到邻居的邻居单元，其不紧致，所以本文使用了其改进后的BR2格式。由式(8a)再经过一次分部积分，得到：
依此定义提升算子Rh=Zh-∇Wh，则在每个单元中Rh可以由式(10)方便的算出(由于使用正交基函数，不用单元体积分)，而∇Wh可以直接得到，因此Zh=∇Wh+Rh无需存储。这就解决了BR1格式计算量和存储量大的问题。但BR1格式不紧致的问题还未解决，为此定义修正提升算子rf为：
其中f是网格中任意相邻单元的共享边，Ω±分别表示边f的两个相邻单元。粘性数值通量计算公式为： 其中ηf为稳定性因子，一般取3。
式(11)将关于边f的修正提升算子rf±定义其两个相邻单元上，使得式(12)中边f粘性通量计算只与此两个相邻单元相关，从而具有紧致性。
最终的离散方程可以写为：
对(13)式右端积分使用高斯数值积分，时间离散使用显式R-K方法或隐式方法即可推进求解。以上可能需要对曲边界进行修正，其他如激波侦测限制[23]、边界条件等限于篇幅在此不再赘述。 2 算例结果 2.1 库埃特流动
为了验证DG/FV混合方法的数值精度阶，首先计算库埃特(Couette)流动问题，此问题描述的是在两个平板y=0和y=H中，由上平板匀速运动所形成的槽道流动。计算条件取上平板速度U=1，温度T1=0.85；下平板温度T0=0.8；粘性系数μ=0.01为常数；槽道高度H=2。计算区域取为[0,4]×[0,2]，左右边界使用周期边界条件，上下边界使用等温壁条件。时间方向离散使用显式R-K方法和局部时间步长技术。计算使用四套网格，粗网格为120个三角形单元，其余网格由粗网格逐次加倍而得。此问题的精确解如下[7]
表 1给出了L2模下密度的计算误差及数值精度阶，此处及下文中各格式括号中的数字表示其设计精度阶。可以看出各阶DG/FV的数值精度阶数均达到了设计精度，同时DG/FV混合方法的计算误差位于低一阶DGM和同阶DGM结果之间，且随着网格加密更接近于同阶DGM结果。表 2给出了几种精度阶的DG/FV与DG格式计算量的定性理论分析，表明DG/FV混合方法计算量小的主要原因是其使用了更少的高斯积分节点。表 3给出了此算例几种方法的数值计算单步时间及比较(使用Level3网格)。从表 2、表 3可以看出DG/FV混合方法计算量是同阶DGM的60%左右，显示出此方法具有明显的计算效率优势。
| 单元数 | L2 Error | Order | L2 Error | Order | L2 Error | Order | L2 Error | Order |
| DG/FV(2) | DGM(2) | DG/FV(3) | DGM(3) |
| 120 | 6.30E-3 | — | 3.01E-3 | — | 1.89E-3 | — | 5.56E-4 | — |
| 480 | 1.50E-3 | 2.07 | 7.51E-4 | 2.00 | 2.59E-4 | 2.87 | 7.23E-5 | 2.94 |
| 1920 | 3.51E-4 | 2.10 | 1.76E-4 | 2.09 | 2.96E-5 | 3.13 | 8.53E-6 | 3.08 |
| 7680 | 7.23E-5 | 2.28 | 4.21E-5 | 2.06 | 3.44E-6 | 3.10 | 9.84E-7 | 3.12 |
| DG/FV(4) | DGM(4) | DG/FV(5) | DGM(5) |
| 120 | 3.39E-4 | — | 9.89E-5 | — | 6.42E-5 | — | 3.98E-5 | — |
| 480 | 1.73E-5 | 4.29 | 7.28E-6 | 3.76 | 2.57E-6 | 4.64 | 1.98E-6 | 4.33 |
| 1920 | 9.06E-7 | 4.26 | 4.40E-7 | 4.05 | 1.11E-7 | 4.53 | 7.53E-8 | 4.72 |
| 7680 | 4.28E-8 | 4.40 | 2.67E-8 | 4.04 | 3.58E-9 | 4.95 | 3.01E-9 | 4.64 |
| 计算方法 | 高斯点上物理量 | 高斯点上通量 | 单元积分 | 边界积分 | 重构 | 总计算量 | 与同阶DGM相比 |
| DGM(2) | 180 | 327 | 216 | 162 | 0 | 885 | — |
| DG/FV(3) | 440 | 351 | 288 | 162 | 216 | 1457 | 57% |
| DGM(3) | 660 | 526.5 | 864 | 486 | 0 | 2536.5 | — |
| DG/FV(4) | 1216 | 550.5 | 1008 | 486 | 576 | 3836.5 | 58% |
| DGM(4) | 1824 | 798 | 2880 | 1080 | 0 | 6582 | — |
| DG/FV(5) | 2784 | 798 | 1728 | 648 | 1296 | 7254 | 58% |
| DGM(5) | 3596 | 1021.5 | 5760 | 2025 | 0 | 12402.5 | — |
| 计算方法 | 单步CPU时间/ms | 与同阶DGM相比 |
| DG/FV(2) | 5.3 | 60% |
| DGM(2) | 8.8 | — |
| DG/FV(3) | 14.9 | 58.6% |
| DGM(3) | 25.4 | — |
| DG/FV(4) | 41.2 | 62% |
| DGM(4) | 66.1 | — |
| DG/FV(5) | 77.4 | 65% |
| DGM(5) | 119 | — |
层流平板绕流问题作为粘性计算的一个标准算例在文献中被广泛研究。本文计算条件是来流Ma=0.1，L=1处，ReL=U∞L/ν∞=106。平板在L=1处截断，平板前为长0.16的对称面，平板距上边界距离为0.01。计算使用的网格参照文献[20]，平板前缘处Δx=1.5×10-4，Δy=8.9×10-5，网格雷诺数ReΔy=89；平板后缘Δx =1.3×10-1，Δy =2.3×10-4，网格雷诺数ReΔy=230。平板前网格点数16，平板上网格点数51，纵向网格点数17，总单元数2144。左边和上方取远场边界条件；右边截断处采用速度外推，压力给定值；下方为对称边界条件+绝热壁面。
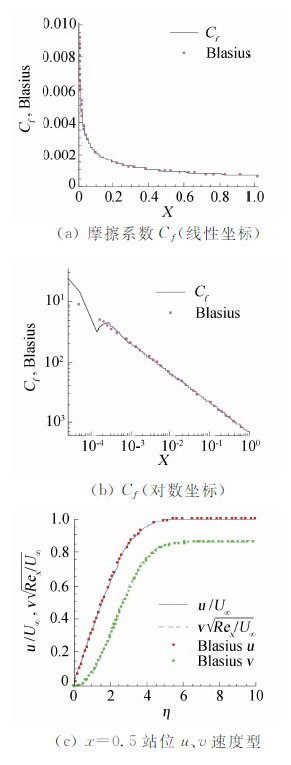
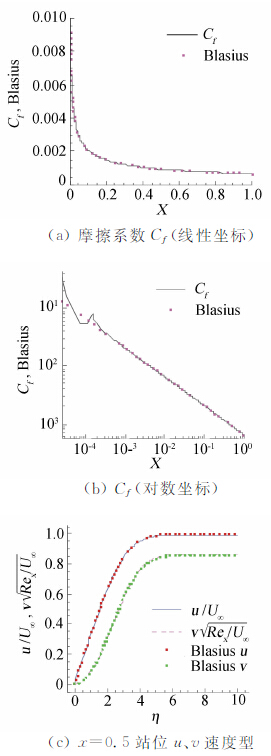
图 1、2、3分别给出了3阶、4阶、5阶精度DG/FV格式计算结果。其中(a)图给出了表面摩擦系数Cf在线性坐标中的分布，可以看到其在图上和布拉修斯解基本重合；(b)图给出了Cf在对数坐标中的分布，可以看到4阶、5阶格式直到离平板前缘约x=10-4处(此处Rex≈100)依然和布拉修斯解重合，而3阶格式只能重合到约x=10-2；(c)图给出了x=0.5站位的u、v速度型，在所用的较粗网格下，可以看到4阶、5阶格式所得的结果与布拉修斯解吻合的很好，3阶格式对于v速度型的模拟稍差一些。图 4给出了5阶格式计算所得密度ρ、速度u、速度v的等值线分布图，可以看到平板前缘附近流场分布很光滑。
 |
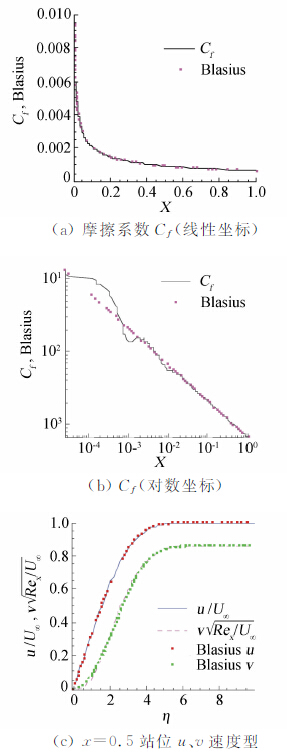| 图 1 三阶DG/FV(3)计算结果Fig. 1 Results of third order DG/FV(3) scheme |
 |
| 图 2 四阶DG/FV(4)计算结果Fig. 2 Results of fourth order DG/FV(4) scheme |
 |
| 图 3 五阶DG/FV(5)计算结果Fig. 3 Results of fifth order DG/FV(5) scheme |
 |
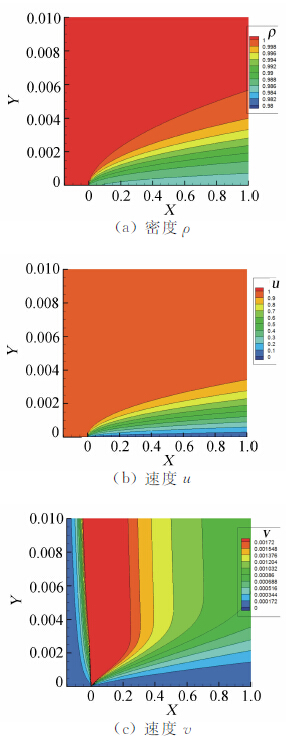| 图 4 五阶DG/FV(5)计算所得流场等值线Fig. 4 Contours of fifth order DG/FV(5) scheme |
本节首先计算来流Ma=0.2、Re=40的定常圆柱绕流问题，使用等温壁，壁温Tw=T∞。圆柱直径d=1.0，计算域为[-15, 30]×[-15, 15]。计算使用两套三角形/矩形混合网格，粗网格及其物面附近放大如图 5所示，其单元数为2395，密网格为粗网格每个单元均匀剖分成四个单元所得，剖分时考虑了曲面外形修正。图 6给出计算所得密度等值线云图、流线分布图和Ma分布云图，使用图 5网格和4阶精度DG/FV(4)格式。图 7给出阻力收敛曲线，计算使用网格和格式同图 6。几种格式计算所得阻力系数Cd和文献结果[24, 25]如表 4所示。从中可以看出DG/FV方法结果与同阶精度DGM结果很接近。对同一网格，随着精度阶提高结果具有收敛性；对于粗密两套网格，最终计算结果也十分接近(四舍五入到三位有效数字时完全一致)。
 |
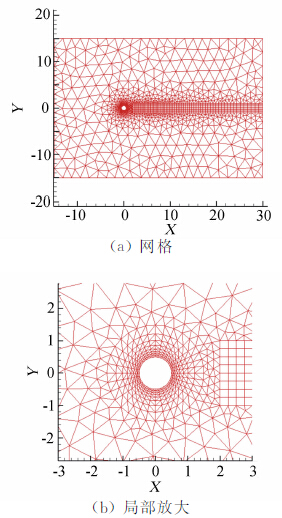| 图 5 粗网格及其局部放大示意图，单元数为2395Fig. 5 Coarse grid with 2395 cells and close-up view |
 |
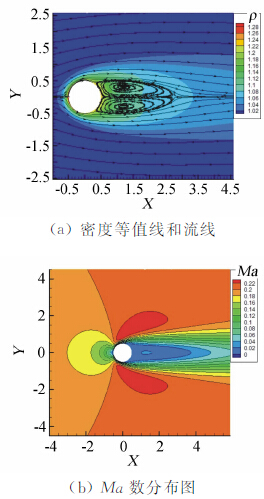| 图 6 (a)密度等值线和流线示意图；(b)Ma分布图Fig. 6 (a) Density contours and streamlines; (b) Mach number contours (grid in Fig. 5,DG/FV(4)) |
 |
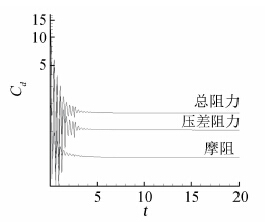| 图 7 阻力系数收敛曲线(图 5网格，DG/FV(4))Fig. 7 History of drag coefficient (grid in Fig. 5,DG/FV(4)) |
| 网格 | 计算方法 | 压差阻力系数 | 摩擦阻力系数 | 总阻力系数Cd |
| Grid1 | DGM(3) | 1.0286 | 0.5453 | 1.5739 |
| 2395 | DG/FV(4) | 1.0329 | 0.5342 | 1.5671 |
| Cells | DGM(4) | 1.0315 | 0.5359 | 1.5674 |
| Grid2 | DGM(2) | 1.0333 | 0.5385 | 1.5718 |
| 9580 | DG/FV(3) | 1.0353 | 0.5359 | 1.5712 |
| Cells | DGM(3) | 1.0343 | 0.5364 | 1.5707 |
| Rogers | 1.017 | 0.532 | 1.549 | |
| Collis | — | — | 1.589 | |
| exp. | — | — | 1.65 | |
本节最后计算非定常状态下的圆柱绕流问题，计算条件是来流Ma=0.2，Re=100，等温壁面Tw=T∞。计算使用图 5网格和三阶R-K时间离散方法，无量纲全局时间步长dt取0.005。图 8给出计算所得瞬时密度等值线、流线示意图和z方向涡量云图，可以看到正负相间的涡量从圆柱表面脱落，涡尺度大约和圆柱直径接近，且随着往圆柱下游，涡量绝对值逐渐变小。图 9给出了升力和阻力系数变化曲线，从中可以看出，大约在无量纲时间t =100以后，升力和阻力曲线出现明显的周期震荡状态。表 5给出几种格式计算所得时均阻力、升力、斯特罗哈数(St)/和文献结果[25, 26]，可以看到DG/FV方法结果与同阶精度DGM结果很接近，和文献以及实验结果有一致性，差异的主要原因可能是采用的计算网格较粗。
 |
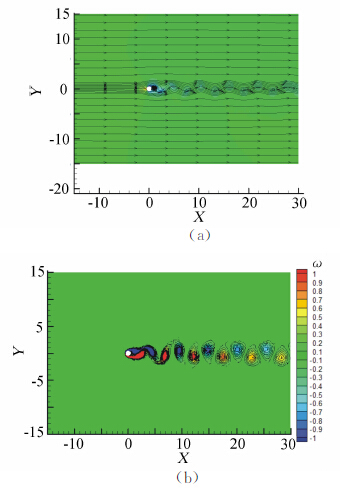| 图 8 (a) 密度和流线示意图；(b) z方向涡量分布图Fig. 8 (a) Density contours and streamlines; (b) contours of vorticity in z direction (grid in Fig. 5,DG/FV(4)) |
 |
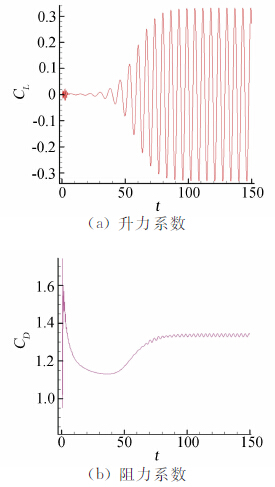| 图 9 升/阻力系数收敛曲线(图 5网格，DG/FV(4))Fig. 9 History of lift and drag coefficient (grid in Fig. 5,DG/FV(4)) |
| 计算方法 | 时均阻力 Cd | 升力ΔCl peak-to-peak | 斯特罗哈数 (St) |
| DGM(3) | 1.3375 | 0.6656 | 0.158 |
| DG/FV(4) | 1.3723 | 0.6865 | 0.161 |
| DGM(4) | 1.3728 | 0.6879 | 0.162 |
| Collis | 1.4107 | 0.6960 | 0.1653 |
| exp. | — | — | 0.165 |
本文将高阶精度DG/FV混合方法推广于二维NS方程的数值模拟，将格式形式精度阶提高到4~5阶。有解析解的Couette流动算例表明方法达到了设计的精度阶，同时DG/FV混合方法的计算误差位于低一阶DGM和同阶DGM结果之间，且随着网格加密更接近于同阶DGM结果；层流平板流动和定常、非定常圆柱绕流等经典算例表明，高阶精度DG/FV混合方法在较粗的网格上亦能得到高精度的计算结果。本文定性理论分析和数值结果表明DG/FV混合方法相比同阶精度DG方法计算量减少约40%。下一步会针对三维复杂外形及湍流流动模拟问题进行研究，并优化算法和程序，尽快在工程问题上有所应用。
| [1] | Wang Z J. High-order methods for the Euler and Navier-Stokes equations on unstructured grids[J]. Progress in Aerospace Sciences, 2007, 43: 1-41. |
| [2] | Barth T J, Frederickson P O. Higher order solution of the Euler equations on unstructured grids using quadratic reconstruction[R]. AIAA Paper 90-0013. |
| [3] | Ollivier-Gooch C, Nejat A, Michalak K. Obtaining and verifying high-order unstructured Finite Volume solutions to the Euler equations[J]. AIAA Journal, 2009, 47(9): 2105-2120. |
| [4] | Cockburn B, Shu C W. The Runge-Kutta discontinuous Galerkin method for conservation laws V: multidimensional systems[J]. J. Comput. Phys., 1998, 141: 199-224. |
| [5] | He L X, Zhang L P, Zhang H X. Discontinuous Galerkin finite element method on 3D arbitrary elements[J]. Acta Aerodynamica Sinica, 2007, 25(2): 157-162. (in Chinese) 贺立新, 张来平, 张涵信. 任意单元间断Galerkin 有限元计算方法研究[J]. 空气动力学学报, 2007, 25(2): 157-162. |
| [6] | Sun Y, Wang Z J, Liu Y. Spectral (finite) volume method for conservation laws on unstructured grids VI: extension to viscous flow[J]. J. Comput. Phys., 2006, 215: 41-58. |
| [7] | Sun Y Z, Wang Z J, Liu Y. High-order multidomain spectral difference method for the Navier-Stokes equations on unstructured hexahedral grids[J]. Commun. Comput. Phys., 2007, 2(2): 310-333. |
| [8] | Wang Z J, Gao H, Haga T. A unifying discontinuous formulation for hybrid meshes[M]. WANG Z J. Adaptive High-Order Methods in Computational Fluid Dynamics. Singapore: World Scientific Publishing, 2011: 423-454. |
| [9] | Cockburn B, Luskin M, Shu C W, et al. Enhanced accuracy by post-processing for finite element methods for hyperbolic equations[J]. Mathematics of Computation, 2003, 72: 577-606. |
| [10] | Ryan J K, Shu C W, Atkins H L.Extension of a post-processing technique for the discontinuous Galerkin method for hyperbolic equations with applications to an aeroacoustic problem[J]. SIAM Journal on Scientific Computing, 2005, 26: 821-843. |
| [11] | Dumbser M, Balsara D S, Toro E F. A unified framework for the construction of one-step Finite Volume and discontinuous Galerkin schemes on unstructured meshes[J]. J. Comput. Phys., 2008, 227: 8209-8253. |
| [12] | Dumbser M. Arbitrary high order PNPM schemes on unstructured meshes for the compressible Navier-Stokes equations[J]. Computers & Fluids, 2010, 39: 60-76. |
| [13] | Luo H, Luo L P, Nourgaliev R, et al. A reconstructed discontinuous Galerkin method for the compressible Navier-Stokes equations on arbitrary grids[J]. J. Comput. Phys., 2010, 229: 6961-6978. |
| [14] | Luo H, Luo L P, Ali A, et al. A parallel, reconstructed discontinuous Galerkin method for the compressible flows on arbitrary grids[J]. Commun. Comput. Phys., 2011, 9(2): 363-389. |
| [15] | Zhang L P, Liu W, He L X, et al. A class of hybrid DG/FV methods for conservation laws I:basic formulation and one-dimensional systems[J]. J. Comput. Phys., 2012, 231: 1081-1103. |
| [16] | Zhang L P, Liu W, He L X, et al. A class of hybrid DG/FV methods for conservation laws II: two-dimensional cases[J]. J. Comput. Phys., 2012, 231: 1104-1120. |
| [17] | Zhang L P, Liu W, He L X, et al. A class of hybrid DG/FV methods for conservation laws III: two-dimensional Euler equations[J]. Commun. Comput. Phys., 2012, 12(1): 284-314. |
| [18] | Wang Z J, Shi L, Fu S, et al. A PNPM-CPR framework for hyperbolic conservation laws[R]. AIAA 2011-3227. |
| [19] | Shi L, Wang Z J, Fu S, et al. A PNPM-CPR method for Navier-Stokes equations[R]. AIAA 2012-460. |
| [20] | Bassi F, Rebay S. A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier-Stokes equations[J]. J. Comput. Phys., 1997, 131: 267-293. |
| [21] | Bassi F, Rebay S, Mariotti G, et al. A high-order accurate discontinuous finite element method for inviscid and viscous turbomachinery flows[C]//Decuypere R, Dibelius G. 2nd European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, Antwerpen, Belgium: Technologisch Instituut, 1997: 99-108. |
| [22] | Roe P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. J. Comput. Phys., 1981, 43: 357-372. |
| [23] | Zhang L P, Liu W, He L X, et al. A shock detection method and applications in DGM for hyperbolic conservation laws on unstructured grids[J]. Acta Aerodynamica Sinica, 2011, 29(4): 401-406. (in Chinese) 张来平, 刘伟, 贺立新, 邓小刚. 一种新的间断侦测器及其在DGM中的应用[J]. 空气动力学学报, 2011, 29(4): 401-406. |
| [24] | Rogers S E. Numerical solution of the incompressible Navier-Stokes equations[R]. NASA TM-102199, November, 1990. |
| [25] | Collis S S. Discontinuous Galerkin methods for turbulence simulation[R]. Center for Turbulence Research Proceedings of the Summer Program, pp.115-167, 2002. |
| [26] | Williamsonc. Oblique and parallel modes of vortex shedding in the wake of a cylinder at low Reynolds numbers[J]. J. Fluid Mech., 1989, 206: 579-627. |