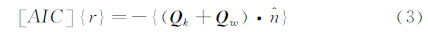0 引 言
近年来,随着风电的持续发展,对影响风力机叶片出力的研究越来越多。风力机叶片周围流场的分布规律决定着风轮的空气动力特性,直接影响着风力机的功率系数[1, 2]。对风机叶片尖端几何作相应的修改,改变叶片下游尾迹分布,减小诱导阻力,提高功率输出[3]。在水平轴风力机叶尖添加各种小翼,可以改变叶尖流场的气流,有效降低叶尖处诱导阻力,减少叶尖能量损失,是目前较为可行的一种方法,特别是在许多叶片尺寸受限的风场。
目前,国内外有多位研究者对各种小翼进行了相应研究。Jeppe Johansen[3]和Alka Gupta[4]采用CFD方法研究了扫掠小翼参数下的功率和扭矩特性。Saravanan P[5]试验研究了小尺寸水平轴风力机增加小翼后的功率系数变化情况。国内张震宇、汪建文、张立茹等[6, 7, 8]同样采用CFD方法研究了叶片增加小翼后的流场变化情况。
涡尾迹理论介于叶素动量理论和计算流体力学之间,采用势流计算,针对旋转机械产生的螺旋形涡结构进行计算,可以求解复杂动态来流时的非定常气动特性,较动量理论和CFD方法具有较好的计算精度和计算效率[9, 10]。涡方法最早由Landgrebe、Kocurek等[11, 12]应用于直升机模拟尾迹和载荷,后由Coton、Dumitrescu、Kocurek等引入到风力机领域分析气动性能[13, 14, 15]。
本文基于直接求解升力面上的气动离散方程,采用自由尾迹模型,建立风力机气动分析程序,分析添加小翼后的风力机叶片气动性能参数的变化。 1 计算方法 1.1 基本假设
假设风力机来流风均匀,稳态,叶片为刚性叶片,因此是周期性流场,在设计和分析过程中实际针对单个叶片进行。假设流动是不可压缩流动,雷诺数足够大,完全满足势流理论条件。 1.2 叶片模型
单叶片参考坐标系如图 1所示,叶片以角速度Ω旋转。限定升力线位于xz平面内,几何升力线可能偏斜出平面。假定平面内任意升力线上一点的向量r(s),s为曲线长度,则该升力线环量强度Γ(s)。速度向量Q为运动速度和诱导速度之和。
式中,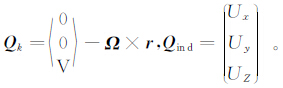
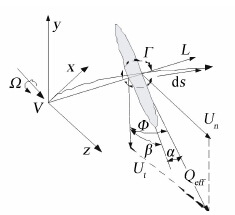 |
| 图 1 叶片参考坐标Fig. 1 Blade reference coordinate |
假定升力线切向单位向量L。根据儒可夫斯基定理[14],可得dL=ρQ×LΓds。无粘性推力和扭矩分别为dTi=z·dL,dQi=z·r×dL。基于切向向量L分析翼型的二维平面流动。考虑升阻比,假设阻力垂直于升力方向,阻力向量为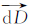 =
ερL×Q×LΓds。同样,粘性推力和扭矩单元分别为dTv=z·
=
ερL×Q×LΓds。同样,粘性推力和扭矩单元分别为dTv=z·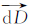 ,dQv=z·r×
,dQv=z·r×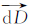 。
。
有效速度向量Qeff=L×L×Q,入流角 翼型升力系数。
翼型升力系数。
为了使求解问题封闭,需要知道升力线和尾缘尾迹的诱导速度。任一点的诱导速度由毕奥-萨伐尔定律[14]可得
式中,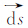 是涡线上的微元,r是涡线到计算点P的距离向量,Γ是微元处的环量。很明显当计算点趋近dl向量时,毕奥-萨伐尔定律有一个奇异点,因为|r|趋于0。
1.3 自由尾迹模型
是涡线上的微元,r是涡线到计算点P的距离向量,Γ是微元处的环量。很明显当计算点趋近dl向量时,毕奥-萨伐尔定律有一个奇异点,因为|r|趋于0。
1.3 自由尾迹模型
涡流理论是通过计算涡流轨迹进行性能分析。由于升力线法不能体现弦长等特性,故采用考虑涡量在翼展和弦长方向变化的升力面模型。任取面上的一段涡线为研究对象,该点的涡线控制方程
式中,[AIC]为气动影响系数矩阵,[AIC(i,j)]={UIC(i,j)+VIC(i,j)+WIC(i,j)}T·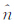 (i,j),t=0时,诱导速度向量Qw={0}。
(i,j),t=0时,诱导速度向量Qw={0}。
根据Sant et al.研究[12],为获得平滑稳定的结果,可引入涡核模型[13]。涡核参数对尾迹形状影响较大,对环量解影响较小。通过引入粘性涡核因子Kv,Biot-Savart方程改写为
式中,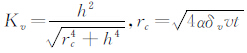 ,参数a=1.2564,δ=100,v=1.5×10-5m2/s,h到涡核的垂直距离。引入涡核模型仅用于计算诱导速速,迭代计算过程中更新尾迹位置。在计算影响系数矩阵时不使用该涡核模型,否则计算结果与势流升力线面理论结果出现较大偏差。
2 模型参数
,参数a=1.2564,δ=100,v=1.5×10-5m2/s,h到涡核的垂直距离。引入涡核模型仅用于计算诱导速速,迭代计算过程中更新尾迹位置。在计算影响系数矩阵时不使用该涡核模型,否则计算结果与势流升力线面理论结果出现较大偏差。
2 模型参数
风力机实际运行时,叶尖受叶片本体带动或风力突变等因素影响,叶片的受风面的压力较大,长期会使叶尖处叶片的背风面发生变形从而导致叶尖损失,叶尖损失会致使叶片不产生升力,大大影响风力机的工作效率。可以考虑在叶尖处增加襟翼或小翼,改变叶片的受力,优化气动性能。
本文研究两种形状的小翼,设计叶片小翼如图 2(a)所示。为便于对比分析,分析上下两个方向相同扭矩系数的小翼对气动性能的影响以及不同高度小翼的气动性能。选取风力机叶片数B=3,λ=8,R=20。翼型参数Cl=1.4,a=8°,ε=1/110(Ris翼型),小翼曲率半径为0.025R。叶片对应的弦长和桨距角如图 3(a)和图 3(b)所示。
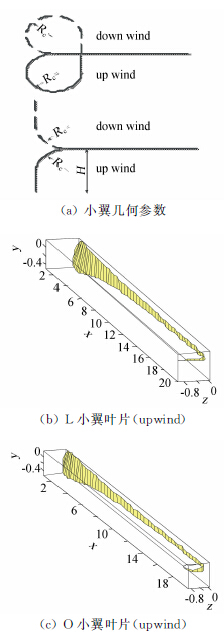 |
| 图 2 叶片几何Fig. 2 Blade geometry |
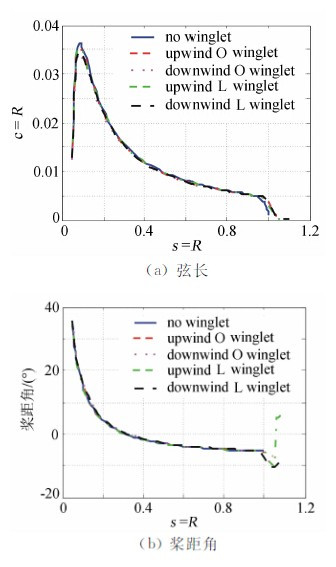 |
| 图 3 弦长和桨距角分布Fig. 3 The distribution of chord and pitch angle |
采用自由尾迹方法研究小翼对风力机性能的影响。图 5为CT=0.8时两种方向小翼在不同高度下的功率系数变化图。可以看出,向下方向的小翼功率系数优于上风向小翼。随着高度的增加,功率系数都呈现上升趋势,下风向小翼功率系数升高明显。
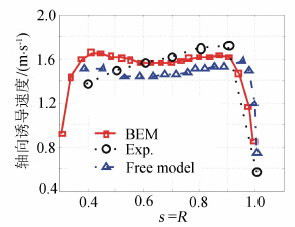 |
| 图 4 轴向诱导速度Fig. 4 Axial induced velocity |
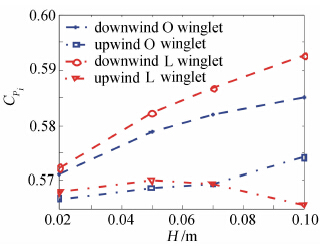 |
| 图 5 不同小翼功率系数Fig. 5 Power coefficient with different winglet height |
为验证模型的有效性及程序设计方法的正确与否,针对文献[16]中风机试验参数及动量理论计算相对比。桨叶处的诱导速度是计算气动性能的关键。图 4为轴向诱导速度沿叶片的分布曲线。可以看出,自由尾迹模型和动量理论都能较好的预测平均诱导速度。说明模型及程序设计可以用来分析气动性能。
图 6是最佳环量分布及不同方向诱导速度的对比。环量分布图显示,增加小翼后,最大环量低于基准叶片,环量分布向外延伸,由于总环量相同,所以相应最大环量减小。L型小翼叶片的诱导速度在三个方向的分量变化较O型小翼变化大。相同小翼时,上风向小翼的诱导速度值高于下风向。主要原因可能是下风向小翼破坏了尾缘尾迹,叶片间尾迹干扰相应减小。上风向小翼的背面与风向相同,小翼的作用效果很小。
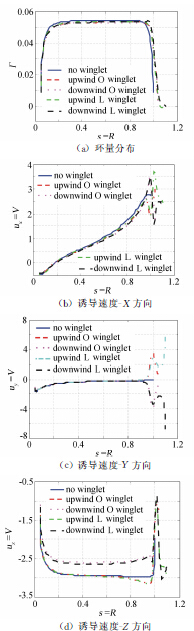 |
| 图 6 环量和诱导速度分布对比Fig. 6 Circulation and induced velocity comparisons |
图 7为叶片扭矩、功率及根部弯曲动量分布曲线。可以看出,两种小翼的功率系数都出现负值,下风向小翼的整体负面效应比上风向的作用小。螺旋形的尾迹旋涡的位移沿扩散方向是不变的,很容易被小翼取代。图 7(a)可以看出,功率系数粘性部分整体往右移动,即能量消耗部分主要在叶尖小翼部分,因此可以看出,能够通过增加小翼改变叶尖涡流分布和流场,改变叶片下游尾迹分布,减小诱导阻力,提高功率输出。由功率系数和根部弯曲动量系数分布看出,小翼的影响主要在局部区域。
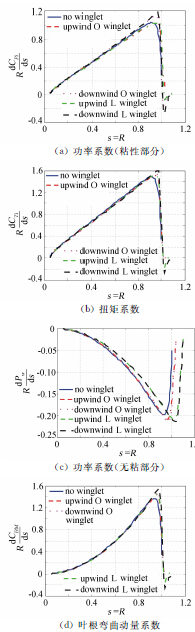 |
| 图 7 功率系数、扭矩系数分布Fig. 7 Power coefficient and thrust coefficient distribution |
图 8为O型小翼叶片旋转尾迹示意图。尾迹扩散非常快,在叶片旋转平面后的短距离内,形状没有变化,同样说明小翼主要作用叶尖区。因此可以通过添加小翼消弱叶尖涡的强度,推迟了叶尖涡产生的时间,使叶尖流动损失降低,从而提高功率输出。
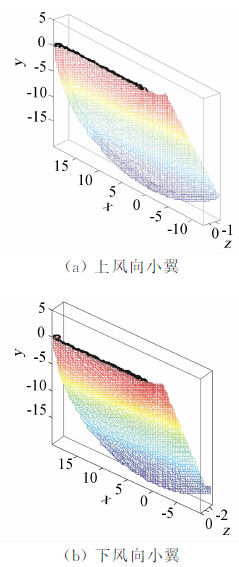 |
| 图 8 O型小翼叶片旋转尾迹Fig. 8 Blade rotor of wake of O winglet |
通过分析叶尖尖部增加小翼后的气动性能和功率输出,发现小翼能够有效提高功率输出,特别是下风向小翼。因此,小翼可作为叶片附加件安装在现有风场风机叶片上或新制造的叶片上,以提高发电效率,特别是在叶片尺寸受限制的风场或地区。 4 结 论
本文采用涡方法分析了叶片增加O型和L型小翼对风力机叶片气动性能的影响。可以看出:
(1) 气动性能方面,L型小翼功率提升优于O型小翼。
(2) 两种方向的小翼都能增加叶轮对功率系数。功率系数增量下方向小翼优于上方向小翼,并且随着曲率半径或高度的增大而增加。
(3) 小翼通过影响叶尖区域涡的强度,改变流场分布,推迟叶尖涡产生的时间,使叶尖流动损失降低。两种小翼的叶根弯曲动量系数沿叶片扩展相应增加,可能引发气动弹性效应,增加叶片疲劳失效,因此,后续需要进一步耦合研究功率系数和扭矩的影响。
| [1] | Baerwald E F, Genevieve H D, Brandon J K, et al. Barotrauma is a significant cause of bat fatalities at wind turbines[J]. Current Biology, 2008, 18(16): 231-142. |
| [2] | Gaunaa M, Johansen J. Determination of the maximum aerodynamic efficiency of wind turbine rotors with winglets[J]. Journal of Physics, 2007, 75(12): 126-132. |
| [3] | Johanse J, Sorensen N N. Numerical analysis of winglets on wind turbine blades using CFD[C]//European Wind Energy Conference, Milan: 2007. |
| [4] | Guptaa, Amano R S. CFD analysis of wind turbine blade with winglets[C]//IDETC/CIE2012, Chicago, 2012: 843-849 |
| [5] | Saravanan P, Parammasivam K M, Selvi R S. Experimental investigation on small horizontal axis wind turbine rotor using winglets[J]. Journal of applied science and engineering, 2013, 16(2): 159-164. |
| [6] | Zhang Z Y, Wang T G, Chen L, et al. Aerodynamic design and numerical optimization for conceptual wind turbine blades with multiple winglets[J]. Acta Aerodynamica Sinica, 2013, 31(1): 127-131. 张震宇, 王同光, 陈立. 分裂叶尖概念型风力机叶片的气动设计与数值优化研究[J]. 空气动力学学报, 2013, 31(1): 127-131. |
| [7] | Wang J W, Quan J J, Wu W Q. Experimental research on power augmentation of a horizontal axis wind turbine with a tip vane[J]. Journal of Engineering Thermophysics, 2008, 29(1): 46-48. 汪建文, 全建军, 吴克启, 等. 风力机叶尖加小翼动力放大特性的试验研究[J]. 工程热物理学报, 2008, 29(1): 46-48. |
| [8] | Zhang L R, Wang J W, Qu L Q. A three-dimensional numerical on flow field of wind turbine with and without tip vane[J]. Acta Energiae Solaris Sinica, 2011, 32(11): 1599-1604. 张立茹, 汪建文, 曲立群. 风力机叶尖有无小翼三维流场的数值研究[J]. 太阳能学报, 2011, 32(11): 1599-1604. |
| [9] | Hansen M O. Aerodynamics of wind turbines[M]. VA: Earthscan, 2008. |
| [10] | Burtont, Sharpe D, Jenkins N Bossanyi E. Wind energy handbook[M]. West Sussex, John Wiley & Sons, 2001. |
| [11] | Kocurek J D, Tangler J L. A prescribed wake lifting surface hover performance analysis[J]. Journal of the American Helicopter Society, 1977, 22(1): 24-35. |
| [12] | Coton F N, Wang T. The prediction of horizontal axis wind turbine performance in yawed flow using an unsteady prescribed wake model[J]. Journal of Power and Energy, 1999, 213: 33-43. |
| [13] | Dumitres H, Cardos V. Wind turbine aerodynamic performance by lifting line method[J]. International Journal of Rotating Machinery, 1999, 4(1): 141-149. |
| [14] | Kocurek D. Lifting surface performance analysis for horizontal axis wind turbines[R]. golden: Solar Energy research institute, 1987. |
| [15] | Santt, Kuik G V, Bussel G J W. Estimating the angle of attack from blade pressure measurements on the NREL phase VI rotor using a free wake vortex model: Axial conditions[J]. Wind Energy, 2006, 9: 549-577. |
| [16] | Tonio S. Improving BEM-based aerodynamic models in wind turbine design cides[D]. University of Malta, 2007. |