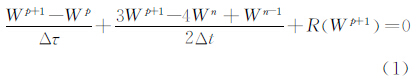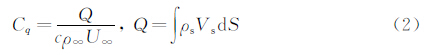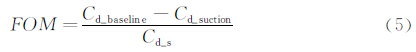2. 南京理工大学 瞬态物理国家重点实验室, 江苏 南京 210094
2. National Key Laboratory of Transient Physics, Nanjing University of Science and Technology, Nanjing 210094, China
0 引 言
低雷诺数(通常是104≤ Re ≤106)条件下[1, 2, 3],翼型表面边界层流动基本处于层流状态,抗逆压梯度能力较弱,容易产生流动分离,从而对翼型升阻比和飞行稳定性等产生严重影响。针对这种情况,人们一直在寻求有效控制流动的方法,试图通过改变飞行器边界层的流动结构,以达到消涡、减阻和提高飞行稳定性的目的。
边界层抽吸控制在抑制分离的应用中十分有效,特别是用于抑制低雷诺数下流动分离的抽吸控制近年来成为研究热点。通过在分离区附近某一部分区域内等间距分布抽吸小孔,应用边界层抽吸以维持未分离的层流边界层,能够减小流动分离引起的阻力并可增加升力。另一个优点是边界层抽吸可以作用在很小的面积上,这样,由于抽吸需求量小,可以减少抽吸控制的能量消耗。陈南茜[4]、白鹏[5]初步研究了采用开缝吸气方式从吸气压力系数和抽吸位置分别对圆柱和三角翼等分离流动的控制效果。Owens[6]等对边界层抽吸抑制高后掠翼的流动分离进行了低湍流度风洞实验研究,结果显示:通过维持前缘附着流动,边界层抽吸有效改善机翼气动性能,使升阻比增加了21%。并发现在无抽吸时,机翼前缘连续微孔结构没有降低机翼气动性能。Wahidi[7]等通过风洞实验研究了低雷诺数下多孔分布式抽吸控制对LA2573a翼型在2°,4°和6°时的控制效果,通过控制分离泡大小和推迟分离,使阻力减小了14%~24%。并通过采用当量抽吸阻力概念,指出抽吸消耗的能量明显小于控制所节省的能量。然而,Wahidi只对三种抽吸流量的能耗问题进行了实验研究,另外,进行实验研究要花费很大的代价,特别是实验中额外的抽吸控制更是需要精细的测量。
虽然前人对抽吸控制已经做了相应的工作,但是抽吸方向对翼型分离流动控制影响的研究较少,而选取何种方向进行吸气控制能够使抽吸以最小的代价达到最大改善翼型气动性能是在实施抽吸控制中必须面对的问题。另外,抽吸系数与抽吸能耗之间的制约问题也未得到充分的研究。基于上述原因,本文在前人研究成果的基础上,以文献[8]中来流雷诺数为10 000,迎角为6°,马赫数为0.2的NACA0012翼型绕流为基准状态,在NACA0012翼型吸力面分离点附近一定范围内通过等间距布置一系列抽吸小孔形成多孔抽吸区域,系统研究了抽吸系数和抽吸角度对附面层抽吸抑制流动分离效果的影响,探索翼型气动性能随抽吸系数的变化规律,寻求翼型性能与抽吸角度的最佳匹配,并对抽吸控制能量消耗进行了相应评估。本文通过数值模拟,给出了清晰细致的物理流动图像,获得各个抽吸控制过程的流场变化信息。这有助于更深层次地理解抽吸控制机理,为流动控制提供新的思路和方法。 1 数值方法简介
本文以无量纲化的积分形式二维非定常Navier-Stokes方程为控制方程,采用格心有限体积法对控制方程进行离散。对流项采用计算精度和计算效率均较高的Roe格式[9]进行离散求解,Roe格式在边界层内具有很高的粘性分辨率,可以准确地捕捉边界层内的流场变化。并采用三阶加权基本无振荡格式(Weighted Essentially Non-Oscillatory,WENO)[10]对流场变量进行重构以使格式达到三阶精度。粘性通量采用二阶中心差分格式离散。
时间推进采用具有二阶精度的双时间步长LU-SGS全隐式算法[11]。通过在方程左端引入伪时间导数项,并对伪时间导数项进行一阶向后Euler离散,得到:
然后将非线性项R(Wp+1)进行线性化带入到式(1)中得到形如{LHS}p·ΔWp={RHS}p的线性方程组,再进行迭代求解。子迭代过程由隐式LU-SGS方法完成,伪时间迭代次数的控制依据为:给定连续性方程的残差均方根相对值作为收敛判据,当残差相对值下降两个数量级时,本物理时间步迭代结束。并采用当地时间步长和隐式残差光顺等措施加速收敛。在低雷诺数流动中,不稳定的大尺度层流结构控制了低雷诺数分离泡的再附和涡的脱落,而湍流仅起到次要作用[12, 13]。并且Elimelech[14]通过对低雷诺数翼型流动的研究,证明层流模型足以求解低雷诺数下的流动结构。本文的计算也证明了这一点,故为了减小计算代价以便详细研究抽吸控制机理,本文采用层流模型。
外边界采用远场边界条件。固壁采用无滑移边界条件。抽吸边界条件为给定抽吸速度大小,并沿一定方向吸入;密度由内部流场值一阶外推得到;压力通过一维绝热流能量方程求出。 2 算法验证
为了验算上述算法的正确性,本文计算模型采用NACA0012翼型,该翼型有着丰富的实验和数值模拟结果。采用椭圆方法生成“C”型网格,以翼型弦长c=1为参考长度。计算条件选取Re=10 000,Ma=0.2的低雷诺数流动,Ohtake等人[8]从实验方面对该流动条件下绕NACA0012翼型流动进行了研究,得到该翼型在低雷诺数下的非线性气动特性。本文首先计算该流动条件下绕NACA0012翼型流动,以对本文数值算法进行验证,同时将该结果作为流动控制的基准状态。在低雷诺数下,绕NACA0012翼型流动会产生流动分离,对NACA0012翼型的气动性能产生严重影响。所以,为了更精细地模拟分离区流动,对NACA0012翼型上翼面后缘和尾迹区进行了加密。通过网格无关性检验,最终选取网格节点数为895×97,其中翼型表面分布了360个网格点。图 1给出了本文计算的升力系数与实验结果的对比,由图可见,在小迎角流动下(α<7°)数值模拟结果与实验值吻合较好,而迎角为8°时,翼型表面流动分离加重,相对于小迎角状态来说,湍流比重逐渐加大,这是导致迎角为8°时出现较大误差的主要原因。
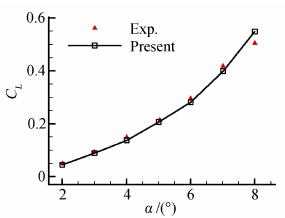 |
| 图 1 NACA0012翼型计算升力系数与实验结果对比图Fig. 1 Comparison of the computational lift coefficients with the experimental results |
图 2给出了迎角为6°的某一瞬时涡量图。从图可以看出,低雷诺数下绕NACA0012翼型流动分离现象是一个非定常过程,翼型前缘涡与后缘涡周期性地产生和脱落,并在尾迹区形成涡街。图 3为低雷诺数流动下,翼型升阻力呈周期性振荡,反映了流动分离对NACA0012翼型气动性能的严重影响。
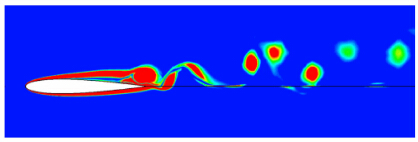 |
| 图 2 迎角分别为6°的某一瞬时涡量图Fig. 2 The instantaneous vorticity distributionsat the angle of attack of 6° |
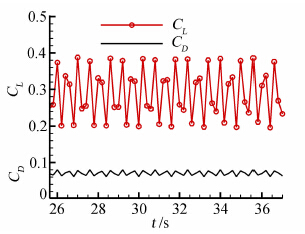 |
| 图 3 迎角分别为6°的升阻力随时间的变化Fig. 3 Variations of lift and drag coefficients with time at the angle of attack of 6° |
综上所述,本文数值算法对于计算低雷诺数、小迎角条件下的翼型绕流具有良好的可靠性和准确性,并能清晰地反映出流动中周期性涡脱落等非定常现象。
Wahidi[7]对LA2573a翼型在低雷诺数下、不同迎角下的抽吸控制进行了低速风洞实验,图 4 给出了迎角为2°的LA2573a翼型抽吸控制前后阻力系数的计算与实验[7]的比较。在抽吸控制下,阻力系数逐渐减小,这与实验值的变化趋势一致。虽然在小抽吸系数下计算与实验的阻力系数值相差较大,但当抽吸系数增大时,其差别逐渐缩小。特别是在大抽吸系数下,计算与实验的阻力系数相差最小,误差约为4.5%,这是因为在大抽吸系数下,分离流动的抑制程度最大,由分离引起的流场脉动、紊乱得到了抑制,流场趋于规整,流动结构简单,降低了复杂流动的模拟对计算格式和网格等的高精度要求,因此误差最小。以上分析表明,本文发展的数值模拟方法能够用于抽吸控制的计算与模拟,特别是在大抽吸系数下的控制研究。
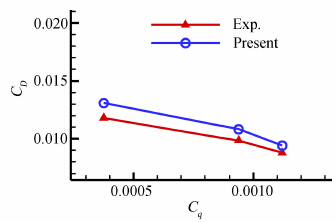 |
| 图 4 抽吸控制下计算与实验结果比较Fig. 4 Comparison between computational and experimental results with suction control |
本文选取NACA0012翼型在迎角为6°时出现的流动分离作为基准状态,采用抽吸控制方法,抽吸方向沿当地物面法向吸入。在翼型吸力面分离点附近一定区域内开孔形成连续多孔表面,通过抽吸方式吸除一部分低能流体,以延迟逆压梯度发生,达到抑制边界层分离,实现对翼型绕流控制的目的。为了更好地模拟边界层流动,壁面第一层网格满足y+=0.5~1.0。抽吸结构参数的设置参考文献[7]中的设计参数,如图 5所示,抽吸区域的起止点为0.15c和0.41c,孔径d为10-3c,孔间距L为10d。θ是抽吸偏角,表示抽吸孔吸气方向与翼型弦线的夹角,边界层内低能流体沿角度θ被吸除。由于孔径相对于弦长很小,为了精确模拟抽吸控制对流场的影响,对抽吸孔周围网格进行了加密,抽吸孔周围网格见图 5。
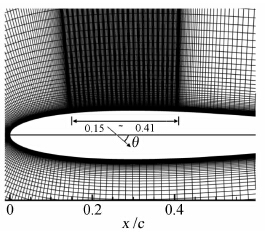 |
| 图 5 抽吸区域示意图Fig. 5 Schematic of suction zone |
首先定义一个无量纲的抽吸系数,它表示单位时间内的质量流率[15]:
c为翼型弦长,Q为被吸入的总的空气质量,ρs为吸气孔处的气体密度,Vs为吸气速度。本文选择涡量分布来定性地反映抽吸控制下流场结构的变化,图 6为4种不同抽吸系数下,绕NACA0012翼型流动的涡量等势分布。与图 2中未控制下涡量分布相比较,发现在这4种抽吸系数下,流动分离和周期性脱落涡都得到了不同程度的抑制,流场也逐渐稳定。当Cq=0.0046时,翼型尾部脱落涡的摆动幅度已经明显减弱;Cq=0.0102时,脱落涡街已经完全消失,尾迹区形成了两条直线;抽吸系数继续增大时,流场结构不再发生显著变化。
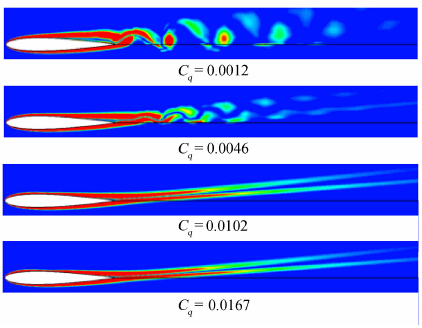 |
| 图 6 四种不同抽吸系数下的涡量分布Fig. 6 Vorticity distributions at four suction coefficients |
为了揭示出抽吸控制的作用机理,图 7进一步给出了抽吸控制前后边界层内时均速度分布的变化趋势,其中抽吸控制对应的抽吸系数为0.0102。可以发现,在x/c=0.1处,由于没有分离发生,速度线型在控制前后几乎一致;而在其余各站位处,由于抽吸控制通过吸除一部分低能流体,翼型表面边界层内的流向动量增加,使边界层内速度梯度明显增大,从而延迟逆压梯度发生,抑制边界层分离。因此,抽吸控制的机理可以概括为:吸除低能流体,增加流向动量,延迟逆压梯度,抑制流动分离。
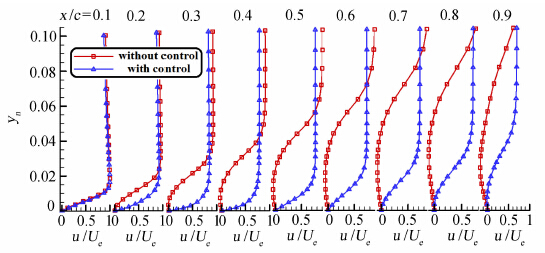 |
| 图 7 抽吸控制前后的时均速度线型的对比Fig. 7 Comparison between mean velocity profiles with and without suction control |
另外,可从升力系数、阻力系数和升阻比三个方面对翼型气动性能随抽吸系数的变化规律进行讨论。图 8给出了6°迎角下NACA0012翼型气动性能随抽吸系数的变化规律,其中对升力系数和升阻比进行了比例缩放。由图可见,升力系数(CL)随抽吸系数的增加而增加,阻力系数(CD)随抽吸系数的增加呈先减小后增加的变化规律,其极小值出现在Cq=0.0046附近,而升阻比(CL/CD)随抽吸系数的增加先是快速增长然后缓慢下降,其极大值出现在Cq=0.0102附近。相对于基准状态值,升阻比极大值提高了约130%,此时,升力系数提高了约72%,阻力系数减小了约26%。
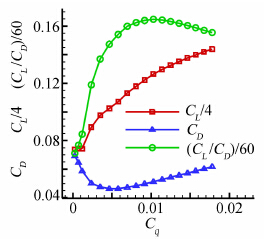 |
| 图 8 NACA0012翼型气动性能随抽吸系数的变化规律Fig. 8 Variations of aerodynamic characteristics of NACA0012 with suction coefficients |
为了进一步揭示该规律的内在原因,在图 9中给出了基准状态与Cq=0.0102时的翼型上下表面时均压力系数(Cp)分布的比较,通过比较可以发现,由于抽吸控制吸除低能流体,延迟逆压梯度发生,使上翼面的压力系数维持较低值;上翼面边界层流动结构的改变,使下翼面的流场受到了影响,压力系数获得了一定程度上的增加,这是导致升力系数获得增加的主要原因。特别是在前缘附近抽吸区域内,相对于无抽吸控制下的压力分布,上、下翼面的压力差明显增加,而且抽吸孔内的低压对升力增加也提供了正贡献,即图 9中有抽吸控制下压力系数曲线跳跃部分表征了抽吸孔内的低压。
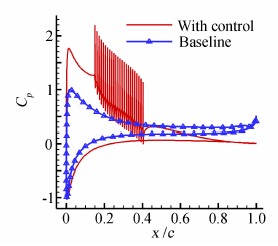 |
| 图 9 压力系数曲线对比图Fig. 9 Comparison of the pressure coefficients |
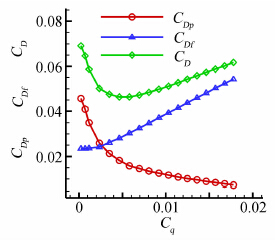
图 10进一步给出了压差阻力系数(CDp)和摩擦阻力系数(CDf)随抽吸系数的变化趋势,从图 10中可以看出翼型压差阻力系数表现为随抽吸系数增加而不断下降,但其变化梯度会逐渐变缓。结合图 6可以看到,在分离点不断后移的同时,翼型上翼面流体附体区域不断增大,同时,由于分离区内的低能流体不断被吸除掉,使边界层内的流向动量增加,壁面剪切力也相应地增加,因此,翼型表面摩擦阻力系数随着抽吸系数增加而不断增加。当Cq大于0.0046,摩擦阻力系数的上涨幅度开始超过压差阻力系数的下降幅度时,总阻力系数开始随着抽吸系数的增加而变大。
 |
| 图 10 压差阻力系数和摩擦阻力系数随抽吸系数的变化Fig. 10 Variations of pressure and friction drag coefficients with suction coefficients |
边界层抽吸控制通过吸除边界层内低能流体,可以有效延迟逆压梯度的发生,抑制流动分离,进而达到增升减阻的目的。但是抽吸控制是一种主动控制方式,它本身需要消耗一定的能量。这就涉及到了能量消耗与因抽吸控制所节省的能量(称之为控制效益)之间的矛盾问题,因此,有必要研究抽吸系数在什么范围内能够保证抽吸控制能耗小于抽吸控制效益。
Bridges引入了一种计算抽吸能耗的方法[16],即认为抽吸所需的能量必须能够使抽吸腔内的低压气体外排到环境中,即公式(3):
其中,Psuction为抽吸所消耗的能量,Pc为抽吸气室内的压强,QV为体积流量。Psuction可以用一个当量吸气阻力Ds来衡量,即Psuction=DsU∞,因此当量吸气阻力系数Cd_s可以表示为:因此,抽吸控制的品质因数FOM(Figure of Merit),
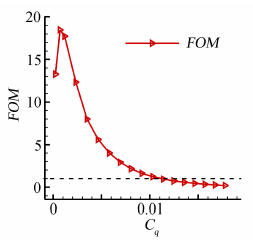
其中Cd_baseline是基准状态的阻力系数,Cd_suction是抽吸控制后的阻力系数。如图 11所示,本文计算了各个抽吸系数下的品质因数,其中图 11中的虚线表示品质因数等于1。结合图 8可以得到,当抽吸系数在小于或等于最大升阻比所对应的抽吸系数时,抽吸控制的品质因数都在1以上,表示在增升减阻时,抽吸控制所消耗的能量明显小于抽吸控制效益,这一点与文献[7]的结论是一致的。然而,Wahidi只对三种抽吸流量进行了实验研究,而本文计算结果则还表明,当抽吸系数进一步增大时,不仅翼型升阻比开始减小,而且抽吸控制品质因数也逐渐小于1,即能量消耗大于抽吸控制效益。综合以上分析,合理的抽吸系数应该满足Cq≤0.0102,此时相对于基准状态,翼型气动性能改善且品质因数皆在1以上。
 |
| 图 11 抽吸控制品质因数随抽吸系数分布Fig. 11 Distributions of figure of merit with suction coefficients for suction control |
通过上述的分析可以看到,在抽吸方向一定的情况下,抽吸系数是决定抽吸效果的关键因素。然而在抽吸孔的设计中,抽吸角度对抽吸控制效果有着至关重要的影响,为此对抽吸角度进行进一步研究,以探求抽吸孔角度的合理设计。
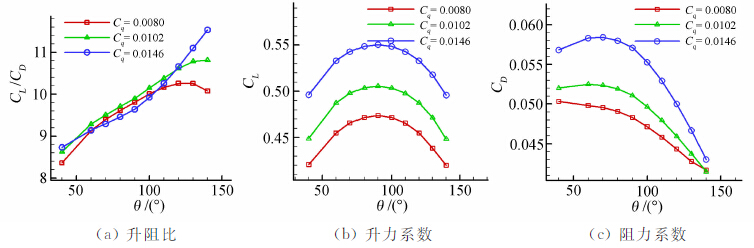
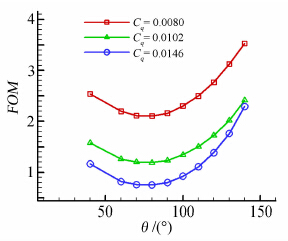
选取Cq=0.0080、0.0102和0.0146三种抽吸系数,研究抽吸角度对抽吸控制的影响,得到如图 12所示的三个抽吸系数下翼型性能随抽吸角度的变化规律。当抽吸角度增加时,抽吸孔内吸气方向由顺主流方向吸入变到逆主流方向吸入。从图 12中可以看出,升阻比总体上随抽吸角度的增加而增加,但在小抽吸系数下,升阻比存在一个极值点;在大抽吸系数下,升阻比呈单调增长的趋势。三种升力系数随抽吸角度的增加都是先增后减,且都在抽吸角度为90°时达到最大值。阻力系数的变化趋势在小抽吸系数时随抽吸角度单调下降;在大抽吸系数时,先有小幅度的上涨然后急剧下降。这是造成升阻比变化率不同的主要原因。为了反映出不同抽吸角度下的能量消耗问题,图 13进一步给出了抽吸控制品质因数随抽吸角度的分布,三条曲线变化趋势显示出在大抽吸角度(θ>90°)时,品质因数都有所提升。因此,结合图 12(a)与图 13,可以看出在大抽吸角度抽吸(θ>90°)时,不仅翼型升阻比会增加,而且抽吸控制消耗的能量会进一步降低。
 |
| 图 12 翼型气动性能随抽吸角度的变化趋势Fig. 12 Variation of aerodynamic characteristics of airfoil with suction angles |
 |
| 图 13 抽吸控制品质因数随抽吸角度的分布Fig. 13 Distributions of figure of merit vs suction angles |
本文以低雷诺下NACA0012翼型分离流动为研究对象,在距翼型前缘0.15c~0.41c范围内布置了一系列等间距的抽吸孔以形成多孔抽吸区域。通过数值模拟,分析了抽吸系数对翼型气动性能和流场结构的影响,不同抽吸方向对抽吸效果的影响,并对抽吸控制能量消耗进行了评估。得到的主要结论如下:
(1) 通过在翼型前缘附近合适位置进行附面层抽吸,可以抑制流动分离,使前、后缘脱落涡逐渐消失,有效改善翼型气动性能。
(2) 抽吸系数是决定抽吸效应的关键参数。随着抽吸系数的增加,升力系数逐渐增大,阻力系数呈先减小后增加的变化规律,而升阻比先是快速增长然后缓慢下降,且相对于基准状态值,升阻比极大值提高了约130%,此时,升力系数提高了约72%,阻力系数减小了约26%。
(3) 通过对抽吸控制消耗能量进行评估,发现当抽吸系数满足Cq≤0.0102时,不仅翼型气动性能得到了改善,而且抽吸控制的品质因数皆大于1,即控制能耗小于控制效益。
(4) 抽吸角度对抽吸控制效果有显著影响,当抽吸角度较大(θ>90°)时,不仅翼型升阻比获得了较大提升,而且抽吸控制的品质因数也会进一步减小。表明合理的抽吸孔设计会进一步改善翼型气动性能,同时有助于减少能量消耗。
| [1] | Selig M S, Guglielmo J J. High-lift low Reynolds number airfoil design[J]. Journal of Aircraft. 1997, 34(1): 72-79. |
| [2] | Ran Jinghong, Liu Ziqiang, Bai Peng. The effect of relative thickness to the dynamic aerodynamic characteristics about pitching airfoils[J]. Acta Aerodynamica Sinica, 2008, 26(2): 178-185. (in Chinese)冉景洪, 刘子强, 白鹏. 相对厚度对低雷诺数流动中翼型动态气动力特性的影响[J]. 空气动力学学报, 2008, 26(2): 178-185. |
| [3] | Bai Peng, Cui Erjie, Zhou Weijiang, et al. Numericalsimulation of laminar separation bubble over 2D airfoil at low Reynolds number[J]. Acta Aerodynamica Sinica, 2006, 24(4): 416-424. (in Chinese)白鹏, 崔尔杰, 周伟江, 等. 翼型低雷诺数层流分离泡数值研究[J]. 空气动力学学报, 2006, 24(4): 4 16-424. |
| [4] | Chen Nanqian. A numerical simulation of unsteady separated flow around a circular cylinder at suction boundary conditions[J]. Acta Aerodynamica Sinica, 1994, 12(3): 287-294. (in Chinese)陈南茜. 吸气条件对圆柱非定常分离流影响的数值研究[J]. 空气动力学学报, 1994, 12(3): 287-294. |
| [5] | Bai Peng, Zhou Weijiang, Wang Yiyun. Investigation of effect of suction on delta wing separation flow at high angle-of-attack[J]. Acta Aeronautica et Astronautica Sinica, 1999, 20(5): 393-398. (in Chinese)白鹏, 周伟江, 汪翼云. 三角翼大迎角分离流开缝吸气效应研究[J]. 航空学报, 1999, 20(5): 393-398. |
| [6] | Owens D B, Perkins J N. Improved performance on highly swept wings by suction boundary-layer control[R]. AIAA 1996-0431. |
| [7] | Wahidi R, Bridges D H. Effects of distributed suction on an airfoil at low Reynolds number[R]. AIAA 2010-4714. |
| [8] | Ohtake T, Nakae Y, Motohashi Y. Nonlinearity of the aerodynamic characteristics of NACA0012 aerofoil at low Reynolds numbers[J]. Journal of The Japan Society for Aeronautical and Space Sciences, 2007, 55(644): 439-445.DOI: 10.2322/jjsass.55.439. |
| [9] | Roe P L. Approximate Reimann solvers, parameter vectors and difference schemes[J]. Journal of Computational Physics, 1997(135): 250-258. |
| [10] | Jiang G S, Shu C W. Efficient implementation of Weighted ENO schemes[J]. Journal of Computational Physics, 1996(126): 202-228. |
| [11] | Rango S D, Zingg D W. Implicit Navier-Stokes computations of unsteady flows using sub-iteration methods[R]. AIAA 1996-2088. |
| [12] | Lin J C M, Pauley L L. Low-Reynolds-number separation on an airfoil[J]. AIAA Journal, 1996, 34(6): 1570-1577. |
| [13] | Li Jianhua, Li Feng. Low-Reynolds-number numerical simulation of inverse zimmerman wing[J]. Acta Aerodynamica Sinica, 2007, 25(2): 220-225. (in Chinese)李建华, 李锋. 机翼低雷诺数流动的数值模拟[J]. 空气动力学学报, 2007, 25(2): 220-225. |
| [14] | Elimelech Y, Arieli R, Iosilevskii G. On the onset of transition at low Reynolds number flow over airfoils[R]. AIAA 2005-5311. |
| [15] | Saeed T I, Graham W R, Babinsky H, et al. Boundary-layer suction system design for application to a laminar flying wing aircraft[R]. AIAA 2010-4379. |
| [16] | Bridges D H. Early flight test and other boundary layer research at Mississippi State 1949-1960[J]. Journal of Aircraft, 2007, 44(5): 1635-1652. |