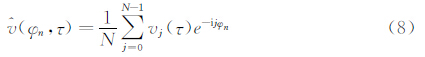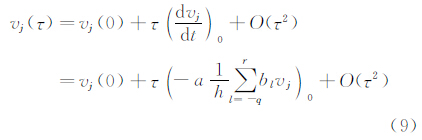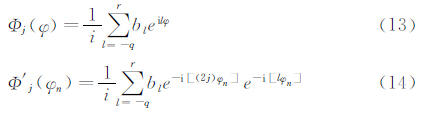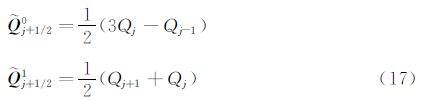2. 国防科学技术大学, 湖南 长沙 410073;
3. 中国空气动力研究与发展中心 计算空气动力学研究所, 四川 绵阳 621000
2. National University of Defense Technology, Changsha 410073, China;
3. Computational Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China
0 引 言
以高速湍流和气动声学为代表的复杂流场中往往包含激波和丰富的尺度，可能跨越多个量级的流动结构，要精确模拟这类流动，需要采用能够捕捉激波的非线性高精度格式。众所周知，数值格式截断误差只是给出了数值解逼近真解的收敛速率，并不能给出在一套具体网格上数值解实际误差的大小。而格式的频谱特性则提供了在一套网格上所有Fourier模态偏离真解的估计[1]。然而，当流场中包含激波时，必须使用能够捕捉激波的非线性格式，这类格式的模板往往具有自适应的特征，且即使用来求解线性问题，也会表现出非线性特性。现有的非线性格式，其非线性机制有多种表达方法，如TVD格式采用通量或斜率限制器[2]，ENO[3]、WENO[4]和WCNS[5]格式采用自适应模板选择来估计数值通量。这种非线性机制的主要作用是激发间断附近的数值耗散以阻止或限制Gibbs振荡的出现。捕捉激波的高分辨率格式，往往包含一个相对应的线性格式，如WENO格式和WCNS格式，将非线性权替换为最优权时格式将退化为线性迎风格式，有人直接以这些线性格式的频谱特性来评价相应非线性格式的频谱特性[6]。然而，数值试验表明非线性机制对数值结果具有显著影响，格式的实际表现同基于线性频谱特性的预测结果具有很大的差异。实际上，同一线性格式，可能对应多个非线性格式，这些非线性格式在模拟同一个流动问题时其表现可能存在明显差异，因此，直接采用非线性格式对应的线性格式频谱特性，显然不能给出这类非线性格式的频谱特性差异。
为了解决此问题，Pirozzoli[7]在定义格式近似色散关系(Approximate Dispersion Relation，ADR)的基础上提出了一种拟线性频谱分析方法，其目的：一是为了量化格式的非线性机制在波数空间对解的影响；二是确定一个误差标尺来作为比较激波捕捉格式的标准。文中对典型激波捕捉非线性格式的分析表明，与传统的线性格式频谱分析结果相比，非线性格式的近似色散关系(ADR)更加准确地反映了非线性格式的特性。尽管该方法并没有包含非线性格式固有的产生虚假Fourier模态及其模态之间非线性干扰对误差的贡献，正如作者Pirozzoli自己评价的那样，该方法至少有两个贡献：一是提供了非线性格式产生的总误差的一个下界；二是提供了一个比较非线性格式特性的基础，这不同于以往文献的只能针对一个个具体算例进行的评价。正因为如此，目前有不少研究者采用此方法来分析所构造的非线性格式的频谱特性，如涂国华等采用此方法比较了5阶WENO格式和5阶WCNS格式的频谱特性[8]，Sun等人也将ADR方法作为其非线性格式参数选取的依据[9]。
拟线性频谱分析方法假设初始流场为约化波数φ的单波，利用空间和时间离散格式将解推进很小的时间步长，并利用离散Fourier变换得到初始情况下和时间推进之后解中约化波数为φ的波的幅值(通常为复数)，通过两个幅值之间的比值可以构造出该约化波数波的近似色散关系。由此得到的ADR公式中包含推进时间步长和空间网格计算点个数两个参数，而且其计算结果与初始单波的相位是相关的。这些参数的不合理选取会造成计算的拟线性频谱具有不确定性。特别是如果计算点数选取不当，拟线性频谱曲线还会出现跳跃点，使得局部区域的频谱特性出现很大的误差，但是Pirozzoli及应用该方法的研究者并未提及这些问题。本文希望通过对以上参数的影响进行研究，提出解决方案，消除以上参数造成的非线性格式频谱计算结果的不确定性，使得ADR公式的使用简单方便，结果准确可靠地反映非线性格式的拟线性频谱特性。
围绕上述目标，发展了与时间离散无关的ADR公式，提出了一种计算点数的选取方法，避免了因计算点数选取不当而使得频谱特性出现不可忽略的计算误差。在此基础上，给出两个三阶非线性加权紧致格式的频谱特性，并通过典型算例，展示了分析方法预测非线性格式频谱特性在定性上的正确性。 1 拟线性频谱分析方法及其改进 1.1 原始拟线性频谱分析方法
对线性波动方程：
在本文中取a=1 。假定初始条件为： 其中φ=ωh为约化波数。此时，初始条件在Fourier空间中包含一对共轭复波。
在式(2)初始条件下，方程(1)的精确解为：
在均匀网格上考虑方程(1)的半离散形式，在xj=jh点: 对于任意显式空间离散格式: 将公式(5)代入公式(4)得到: 其中Φ(φ)为格式的修正波数，对于谱格式有Φ(φ)=φ，对其他离散格式Φ(φ)则会偏离φ，其偏离程度就可以反映离散格式模拟该约化波数波的准确程度。
对于非线性格式，Pirozzoli[7]人为定义了一个近似色散关系(ADR):
其中
0为初始条件下φ模态对应的Fourier系数，(φ,τ)为τ时刻解vj(τ)(对解进行时间步长为τ的推进得到，为避免时间离散方法对分析结果产生重要影响，τ应取一个小量)进行(离散)Fourier变换得到约化波数为φ的模态所对应的Fourier系数。对于公式(2)的初始条件
。
对于某网格(计算域为[0,L]，j=0,…N，h=L/N)，可以支持的模态为λn=L/n(n=0,…,N/2)，对应的约化波数为
。对某一约化波数(φn)的波，对应的Fourier系数可以采用离散Fourier变换(DFT)得到
ADR公式(7)得到的频谱特性实际上是推进时间步长τ的函数，Pirozzoli只是建议将τ取很小的值来降低时间离散造成的影响，但并没有对τ的影响进行详细研究。时间离散方法及其推进步长选取的随意性，会给结果带来不确定性，如果选取不当，甚至得到错误的结果。本文根据时间推进步长是一个小量的假设，推导得到与时间离散无关的ADR公式。对vj(τ)进行Taylor展开:
并将其代入DFT计算公式(8)中，可以得到: 将公式(10)代入公式(7)，并让τ→0: 显然，原始ADR公式(7)所计算的频谱特性实际上是公式(11)所对应频谱关系的数值逼近。公式(11)已经不再包含时间τ，而且不再需要进行时间推进，仅仅通过初始流场就可以得到时间无关的拟线性频谱特性(ADR-No Time parameter,ADR-NT)。与原始ADR公式相比，既降低了方法使用的难度、减少了计算量，又消除了由于时间离散引入的计算误差[10] 1.3 ADR-NT公式的进一步简化及其物理意义
如果初始条件固定为单频余弦谐波并将初值代入计算公式，公式(11)可以进一步简化为:
其中:
当采用线性格式(格式中系数bl为与流场无关的常数)离散时，Φ(φn)=Φj(φ)(j=0,…,N)，
Φ′j(φn)=0，公式(12)将退化为线性格式频谱计算表达式，此时，单一模态的波仍然保持为单一的模态。当采用非线性格式(格式中系数bl为与流场变量相关的函数)离散时，Φ′j(φn)≠0体现了共轭复波之间的干扰对拟线性格式频谱特性的影响，而Φ(φn)－{Φj(φn)+Φ′j(φn)}≠0表明非线性格式将产生其他模态的波。
2 拟线性频谱分析方法中参数的影响研究
本节基于3阶精度HWCNS格式，研究ADR公式中各种不同参数的影响。3阶精度HWCNS格式对一阶空间导数的离散形式为：
其中，h为网格长度，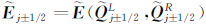
为半节点上的数值通量，
是插值得到的半节点左右变量。半节点上左右变量采用3阶加权非线性插值得到(只给出
的计算公式,
计算公式与
对称)，为了书写简洁，下文中将省略上标“L”：
其中
为子模板上的2阶精度插值函数。ωk为子模板上的非线性权，其计算公式为：
αk可以采用多种计算方法给出，本文给出(19)和(20)两种具体形式，格式分别记为HWCNS3-A和HWCNS3-B。
其中ε为小正数，以避免分母为零。βk为子模板上的光滑测试因子。d0=1/4,d1=3/4为子模板的线性权或者最优权，对应的线性格式记为UPW3。
2.1 时间步长的影响
公式(11)和公式(12)(分别记为ADR-NT和ADR-AV)应该是公式(7)(记为ADR)时间趋向无穷小时的极限，当时间步长τ足够小时ADR应该得到与ADR-NT和ADR-AV相同的结果。下面通过算例展示ADR公式中时间步长τ对计算结果的影响，空间离散格式采用HWCNS3-B，计算网格点数N=422。
图 1给出了双精度情况下计算得到的频谱曲线的实部和虚部，展示了公式(7)的计算结果与时间步长的相关情况。当时间步长逐渐减小时，公式(7)的计算结果逐渐趋近于公式(11)和公式(12)的计算结果。当时间步长较大时，时间离散格式的特性将会影响ADR计算结果，结果将偏离所要得到的空间离散格式的频谱，在τ=10-4时计算结果仍然与公式(11)和公式(12)的计算结果有可见的差异。
 |
| 图 1 双精度情况下时间步长对ADR的影响Fig. 1 Influence of time step on ADR with data of double precision |
图 2给出了单精度情况下的计算结果的实部，基本规律与双精度情况下相同。然而当τ太小时，ADR的计算结果也出现问题，这主要是由于计算机数字舍入误差引起的。
 |
| 图 2 单精度情况下时间步长对ADR的影响Fig. 2 Influence of time step on ADR with data of single precision |
除了时间步长，ADR公式中包含计算点数N和初始相位角θ两个参数，因为单频谐波的更一般形式为u(x,0)=0cos(ωx+θ)(当θ=－π/2是就转化为正弦谐波)。图 3给出了在θ=0和θ=0.25π两个初始相位角下N=120和N=122时计算得到的拟线性频谱。当N=122时计算得到的频谱曲线是光滑的，两个初始相位角的结果差异可以忽略(只给出一条曲线)。然而当N=120时，在某些点上会出现跳跃，不同初始相位角的计算结果存在明显差异。图 4进一步给出了N=120时，φ30=π/2和φ29=29π/60两个典型约化波数计算得到的修正波数(实部)随初始相位角的变化情况。从结果，φ29=29π/60计算结果几乎不随初始相位变化，此时，修正波数的最大计算误差仅有0.001%(“精确解”的计算方法将在下文中利用公式(21)给出)；φ30=π/2时，修正波数随初始相位角变化剧烈，最大误差可达到28.5%。由此可见，计算点数和初始相位角这两个参数可能会对非线性格式的拟线性频谱产生较大的影响。
 |
| 图 3 计算点数与初始相位角对ADR的影响Fig. 3 Modified wave number vs grid points and initial phase angle |
 |
| 图 4 不同初始相位角的修正波数Fig. 4 Modified wave number vs different initial phase angles |
下面我们分析产生以上现象的原因。公式(12)表明ADR公式确定的频谱关系实际上是各点所定义的频谱关系的简单代数平均(标记为ADR-AV)，其实质就是间隔相同的不同相位点上的频谱关系的代数平均。对于某一固定约化波数的波，非线性权值实际上是由计算点所处的相位位置完全确定的，由此计算的Φj(φn)也就由约化波数和计算点的相位完全确定。对于波长为λn=L/n的波，计算域中包含有n个完整的波，如果波长λn与网格长度h没有特定的倍数关系(例如，7个波长为60个网格长度)，那么每个完整波形中网格点所处的相位不会出现周期性，如图 5所示。因此，当波形足够多(N足够大时)，公式(12)的代数平均将包含各个不同相位位置上的频谱，最终频谱关系将和初始相位无关。如果波长λn与网格的长度h存在特定的倍数关系(例如，N=120，φ30=π/2，λ30=4h)，此时网格点所处的相位位置是周期性的，如图 6所示，无论N有多大，公式(12)所做的平均都仅包含几个特殊的相位点。因此，对这些特殊约化波数的波，计算得到的频谱结果都不可避免地受初始相位的影响。图 3中频谱曲线中跳跃点正是处于这些特殊点上，而当N=122时，没有约化波数的波满足这种倍数条件，故所获得的频谱曲线是光滑的。
 |
| 图 5 一般情况下网格点在正弦波上的分布Fig. 5 Distribution of grid points on the sinusoidal wave at non-special wave number |
 |
| 图 6 φ30=π/2时网格点在正弦波上的分布Fig. 6 Distribution of grid points on the sinusoidal wave at wave number of φ30=π/2 |
我们可以采用两种方法来解决图 3中非线性频谱不光滑且对初始相位角非常敏感的问题。第一种，通过对计算网格点数N进行限制消除相位相关性。通常情况下N要求为偶数(N为奇数情况下φn无法取到π)，我们假设N=2Nh(其中Nh为正整数)。从以上的分析可知，只要取Nh为一个质数，就可以避免图 6所示的情况发生，正如图 3中Nh=61时所给出的修正波数结果，不仅曲线光滑，而且两个初始相位角的结果差异可以忽略。
第二种，通过不同初始相位修正波数的代数平均消除相位相关性。从数学的角度看，ADR方法实际上是不同相位点上的非线性修正波数的代数平均，我们也可以对不同初始相位的修正波数进行代数平均来消除初始相位的影响。
其中，θk为不同的初始相位角。将θk取为[0,2π]内均匀分布的初始相位。图 7给出了该方法的计算结果，可以看到，未进行代数平均之前，在部分特殊点，拟线性频谱会随着初始相位角的变化发生较大的跳跃，然而代数平均之后的计算结果是光滑的。对于图 4中φ30=π/2我们同样采用公式(21)进行了计算，计算结果表明当M=60时，计算结果在7位有效数字内已经与“精确解”完全相同(“精确解”采用公式(21)M=2000进行计算)。可以看到公式(21)对应的第二种方法可以有效消除初始相位的影响，然而这种方法计算量较大，在下文中我们重点对第一种方法进行讨论，仅仅应用公式(21)的第二种方法验证两种方法是否能够收敛到相同的计算结果。
 |
| 图 7 初始相位平均ADR计算结果(Nh=50)Fig. 7 Results of ADR using initial phase averaging (Nh=50) |
下面我们讨论第一种消除初始相位相关性的方法达到初始相位和计算点数对修正波数的影响可以忽略时，Nh的取值范围。图 8给出了频谱曲线随Nh的变化情况，其中给出了Nh=997的频谱曲线作为“精确解”。可以看到，当Nh较小时，计算得到的修正波数与“精确解”存在较大偏差，Nh=23仍然可以明显观察出偏差，而当Nh≥41时，计算得到的修正波数已经观察不出偏差。我们同时给出了Nh=60时，通过初始相位平均方法得到频谱曲线，计算点上的修正波数同样可以收敛到“精确解”。图 9给出了图 8中不同曲线相对“精确解”的差异。同样可见，初始相位平均法的计算结果与Nh取足够大质数时的计算结果是一致的，不同Nh得到的修正波数曲线在大约化波数区间中存在相对较大的差异，且Nh为大于40的质数时，初值初始相位和计算点数对修正波数计算结果的影响可以忽略。
 |
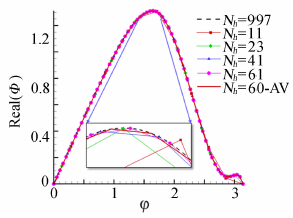| 图 8 ADR 的收敛性Fig. 8 Convergence property of ADR |
 |
| 图 9 计算点数对频谱曲线误差的影响Fig. 9 Influence of grid points on the error distribution of ADR |
基于上文的研究结论，采用ADR-NT公式，Nh=41，对3阶精度HWCNS格式频谱特性进行研究。图 10给出了HWCNS3-A和HWCNS3-B格式的拟线性频谱曲线。尽管HWCNS3-A和HWCNS3-B格式对应的线性格式是完全相同的，ADR公式预测的拟线性频谱表现却有很大的差异。HWCNS3-B格式的色散误差(实部)和耗散误差(虚部)都明显小于HWCNS3-A，特别是耗散误差，HWCNS3-B格式的耗散在很大的范围内都明显小于HWCNS3-A格式。图 10同时给出了
的分布曲线，可以看到共轭复波之间的干扰，对格式的耗散特性的影响比色散特性要显著，且对HWCNS3-B格式的影响明显小于HWCNS3-A格式。
 |
| 图 10 不同格式拟线性频谱对比Fig. 10 Comparison of the quasi-linear spectral of different schemes |
在气动声学问题，流动结构的波长和波幅可能会比噪声的波长和波幅大几个量级，基于此背景，流场初始条件取为：
其中公式(22)中第一项是波长为L的低频波，代表流场中大尺度的流场结构。公式(22)中第二项代表不同频率的声波，其中系数A反映了声波波幅的相对大小。
根据频谱特性预测波在传播过程中波幅为：
另外，数值计算可以得到波幅的变化情况。通过两者的一致程度就可以评估ADR公式预测格式频谱特性的准确程度。利用公式(1)的线性方程进行计算(a=1)，下面给出φ=φn≈1.5的计算。
图 11给出了A=0.001、A=0.01和A=0.1时HWCNS3-A和HWCNS3-B格式计算得到波幅衰减曲线，同时也给出了格式拟线性频谱特性预测的衰减曲线。从结果看，三种情况，HWCNS3-B格式的计算结果都要优于HWCNS3-A格式的计算结果，同上文分析结论一致，但在预测准确度上，存在明显差异。
 |
| 图 11 不同非线性格式波幅衰减曲线Fig. 11 Amplitude decay curves of different nonlinear schemes |
上文ADR公式计算非线性格式的修正波数曲线时，都采用了相应频率的余弦波作为初始条件，因此，得到的是非线性格式的拟线性频谱特性(Quasi-Linear ADR，为了与上文统一将其标记为ADR)。式(7)或式(11)定义的修正波数计算方法，可以推广应用于更加一般的初始条件，从而体现出不同频率波之间干扰对非线性格式频谱特性的影响，所得到的修正波数曲线为非线性频谱特性(Non-Linear ADR)。因此，可以进一步根据非线性频谱特性，来评价非线性格式对噪声的模拟能力及其评价的正确性和准确性。
图 12给出了HWCNS3-B格式在公式(22)初始条件下的非线性频谱。图中给出了不同幅值情况下得到的非线性频谱，为了便于对比，同时给出了拟线性频谱和线性格式UPW3的频谱。可以看到，当A较小时(A=0.001时)，计算得到的非线性频谱接近UPW3线性格式的频谱；当A较大时(A=0.1时)，计算得到的非线性频谱非常接近拟线性频谱；而当A=0.01时，得到的非线性频谱处于线性频谱和拟线性频谱之间。当A较小时，公式(22)第二项所叠加的高频波幅值非常小，最终非线性权的大小将主要由第一项的低频波决定，计算得到的非线性权也将非常接近最优权，得到的非线性频谱将非常接近线性频谱。随着A逐渐增大，高频波的贡献将越来越大，计算得到的非线性权也逐渐由高频波主导，非线性频谱曲线也就会接近拟线性频谱曲线。
 |
| 图 12 非线性格式在气动声学模型问题中的频谱Fig. 12 Spectral property of different nonlinear schemes in the aero-acoustic model problem |
图 13、图 14和图 15分别给出了A=0.001、A=0.01和A=0.1时波幅的衰减曲线，空间离散格式采用HWCNS3-B，三种情况综合来看，非线性频谱结果都给出了最准确的预测，而其余频谱结果的预测均有不足，因为非线性频谱特性比较准确地反映了三种情况下两个频率波的干扰特性。
 |
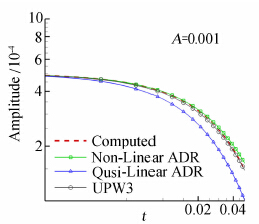| 图 13 波幅衰减曲线(A=0.001)Fig. 13 Amplitude decay curves (A=0.001) |
 |
| 图 14 波幅衰减曲线(A=0.01)Fig. 14 Amplitude decay curves (A=0.01) |
 |
| 图 15 波幅衰减曲线(A=0.1)Fig. 15 Amplitude decay curves (A=0.1) |
钝锥球头半径Rn=27.94mm，半锥角为15°，长度为球头半径的16倍。计算条件：M∞=10.6，Re=3.973×106m-1，T∞=47.3K，Tw=294.44K，α=20°。不计头部，全模计算网格大小为111×221×101(流向×周向×法向)，物面网格雷诺数ReΔ≈4，计算网格被剖分为13块，如图 16所示。
 |
| 图 16 钝锥算例计算网格拓扑Fig. 16 Grid topology of blunt cone case |
图 17给出了不同子午面上的热流分布，并与实验结果进行了对比(三族曲线分别对应于θ=180°,θ=90°,θ=0°)。解的准确的程度不仅与计算格式相关，同时也会受网格的分布影响，本文采用的计算网格较密，因此所有格式都得到了相对较好的计算结果，且HWCNS3-B结果与实验符合程度优于HWCNS3-A，这与ADR方法给出的拟线性频谱特性结果一致。
 |
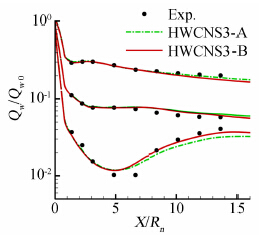| 图 17 钝锥算例热流计算结果Fig. 17 Heat flux computation results of blunt cone case |
针对Pirozzoli为非线性格式提出的拟线性频谱分析方法在使用过程中的不足，比较深入地研究了时间步长、计算点数和单频谐波初值初始相位对非线性格式频谱特性计算结果的影响，获得了以下结论：
(1)通过理论推导，发展了时间离散无关的拟线性频谱分析方法，完全剔除了时间离散对非线性空间离散格式频谱特性计算的影响；且时间离散无关的ADR公式清楚地体现了格式非线性导致的共轭复波干扰的影响及其产生二次波的机制。
(2)基于ADR的拟线性频谱分析方法是Fourier线性频谱分析方法的一种推广，当采用ADR-NT公式分析线性格式的频谱特性时，ADR-NT公式自动退化为Fourier线性频谱分析公式。
(3)找到了计算网格点数和初值相位对非线性空间离散格式的拟线性频谱特性的影响原因，提出了两种消除影响的方法：①计算网格点数为足够大质数的2倍；②均匀抽取足够多个初始相位得到的结果进行代数平均。并且两种方法收敛到相同的拟线性频谱曲线。对于本文的三阶格式，该质数大于40即可，控制计算网格点数的方法更加简便易行。
(4)利用两个三阶精度WCNS非线性格式完成了两个典型算例的计算，结果表明采用ADR公式获得的拟线性频谱能够在定性上评价它们精度的优劣，但定量上仍存在不足。
尽管ADR公式给出的拟线性频谱特性在一定程度上反映了格式非线性特性的影响，但仍然没有体现非线性格式虚假波的产生、不同频率波之间的非线性干扰等复杂的非线性机制。因此，将进一步发展和完善非线性格式频谱分析方法，更加准确地评估它们的特性。
| [1] | Colonius T, Lele S K. Computational aeroacoustics: progress on nonlinear problems of soundgeneration[J]. Progress in Aerospace Sciences, 2004, 40: 345-416. |
| [2] | Osher S, Chakravarthy S R. High resolution schemes and the entropy condition[J]. SIAM J. Numer. Anal., 1984, 21: 955-984. |
| [3] | Harten A, Engquist B, Osher S, et al. Uniformly high order essentially non-oscillatory schemes, iii[J]. Journal of Computational Physics, 1987, 71(2): 231-303. |
| [4] | Jiang G S, Shu C W. Efficient implementation of weighted eno schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. |
| [5] | Deng X G, Zhang H X. Developing high-order weighted compact nonlinear schemes[J]. Journal of Computational Physics, 2000, 165(1): 22-44. |
| [6] | Weirs V G, Candler G V. Optimization of weighted eno schemes for dns of compressible turbulence[A]. 13th AIAA Computational Fluid Dynamics Conference[C]. 1997. Snowmass Village, CO: AIAA 1997-1940. |
| [7] | Pirozzoli S. On the spectral properties of shock-capturing schemes[J]. Journal of Computational Physics, 2006, 219: 489-497. |
| [8] | Tu G H, Deng X G, Mao M L. Specral property comparison of fifth-order nonlinear WCNS and WENO difference schemes[J]. Acta Aerodynamica Sinica, 2012, 30(6):709-712. (in Chinese)涂国华, 邓小刚, 毛枚良. 5阶非线性WCNS和WENO差分格式频谱特性比较[J]. 空气动力学学报, 2012, 30(6):709-712. |
| [9] | Sun Z S, Luo L, Ren Y X, et al. A sixth order hybrid finite difference scheme based on the minimized dispersion and controllable dissipation technique[J]. Journal of Computational Physics, 2014, 270: 238-254. |
| [10] | Mao M L, Deng X G, Li S. Spectrum characteristic of dissipative compact schemes and application to couette flow[J]. Chinese Journal of Computational Physics, 2009, 26(3):371-377. (in Chinese)毛枚良, 邓小刚, 李松. 耗散紧致格式的频谱特性研究与应用[J]. 计算物理, 2009, 26(3):371-377. |