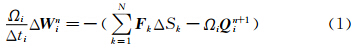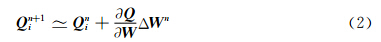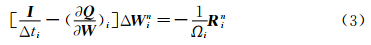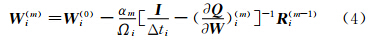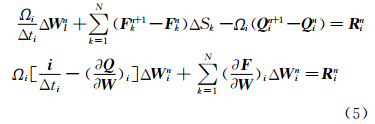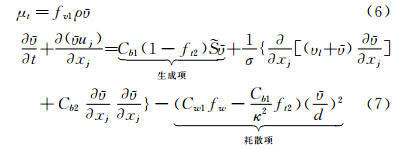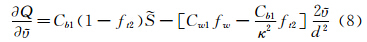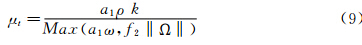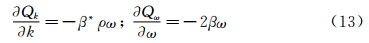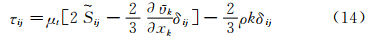当前,基于涡粘假设的湍流模型在湍流工程计算中得到了广泛的应用。与一般NS控制方程相比,涡粘湍流模型方程除了时间导数项、对流项和扩散项可与之相互对应外,最显著的区别在于方程中增加了源项。源项的存在一方面可以集中反映了湍流在空间上的尺度多重性和时间上的高频脉动性[1],但另一方面也导致方程数学性态的复杂变化而产生收敛困难、迭代不稳定等一系列问题,甚至可以说源项处理的好坏直接影响着最终对湍流模拟的效果[2]。
基于此,本文首先对湍流模型方程源项数值求解面临的数值刚性问题进行讨论,其次结合当前应用最为广泛的S-A一方程模型和k-ω SST两方程模型,较为详细的分析了源项的影响,比较了不同的处理手段并以RAE2822翼型跨声速数值模拟为算例对结果进行验证。 1 源项的数值特性分析
一般所指的湍流模型方程源项包括生成项和耗散项两部分,每项都耦合了时间特性和空间特性变量,模拟了湍流量生成和消失的过程,在这个过程中平均流动量演化过程和湍流量演化过程联系在一起,对流动计算的结果起到了很大的影响[3]。
理论分析指出[2],湍流方程源项使得流动变量在时间尺度和空间尺度上发生了剧烈的变化,而这个尺度往往远小于NS方程的离散尺度,尤其是时间尺度随着源项非线性程度的加大会进一步减小,即显著增大了控制方程组的刚性。此时方程很容易丧失正定性,湍流变量无限制增长,源项大范围为负,运算很快发散。从方程稳定性上考虑,这些就要求在确定时间步长时要分别分析对流项、扩散项和源项的当地步长取其最小值,同时网格的长宽比、稠密度等也要有更为严格的限制。但这些措施无疑会大大降低控制方程组的收敛速度,而且根据文献[4],很多时候即便如此也会产生严重的收敛震荡和非物理解。针对这一问题比较通用的做法是将源项做点隐式处理[4, 5]。对于某个单元i,离散后的方程为:
其中Ω表示这个单元的体积,W 表示控制变量,F kΔSk表示某个面的各个通量和,Q 表示源项。
可以看出,此时源项为新时刻(n+1)的值,根据n时刻的结果有:
代入式(1)后整理,最终公式为
其中 i 为单位矩阵,R nI为当前步的残差。若采用m步Runge-kutta方法求解,进一步:为提高控制方程稳定性,减少求解时对CFL数的依赖,也可用LU-SGS方法隐式求解式(3):
但由于源项的高度非线性,很多时候直接求解其雅可比矩阵∂Q /∂W 难度很大,为此可对源项中的生成项和耗散项分别处理,有选择的隐式求解[6]或者仅对源项的负部求解雅可比矩阵[6, 7]。
另外,生成项和耗散项物理意义不同,这也产生了一个源项自身平衡的问题。对于许多湍流模型方程,生成项与涡量的模成正比,直观来看剪切越强,湍流越强,生成项越大。也就是说生成项是湍流强弱的“正尺度”标量,其大小密切关系着湍动能量的注入,是湍流模型方程的主导项,因而对其正定性有着有更为严格的限制。这一点也与零方程模型仅靠正定的生成项自身就能较好模拟附着流动相吻合[2]。对于耗散项,湍流粘性系数越大,耗散越大,对生成项的限制也就越大。为了在边界层区域得到较大的耗散,S-A一方程模型和k-ω SST两方程模型都引入了壁面距离函数[8]。但由于壁面附近网格的间距往往非常小,很小的数值计算误差可能被放大到超过生成项自身产生了违反物理本质的负源扩散(S-A模型),也可能使得生成项不受耗散项制约增大湍动能无限增长(k-ω SST模型)——这些都将导致数值模拟的不稳定。考虑到这些问题,后文将对S-A一方程模型和SST k-ω两方程模型的生成项和耗散项平衡问题进行具体讨论并给出相应处理办法。 2 S-A湍流模型的源项处理与算例分析
S-A湍流模型直接假设其满足流场中的带源项的对流-扩散标量方程,其中包含了大量的经验常数、经验函数。该模型对航空领域的复杂流动模拟取得了很好的效果。全湍流S-A模型方程可以写为:
方程中常数的具体取值可参考文献[9]。观察S-A模型方程,其生成项和耗散项为分别为工作变量 的近似线性和二次函数,因此可判断源项对原模型方程性态影响较弱。源项的雅可比系数可直接近似写为:
尽管S-A源项产生的附加刚性较小,很多时候仍然出现了收敛困难的情况。进一步分析,一方面由于耗散项的二次函数保证其始终为负,不会出现在迭代计算中生成项缺乏限制过大产生的湍流量无限增长的情况。但另一方面,壁面处工作变量 u=0是S-A模型方程在实际应用中给定的边界条件,当壁面网格非常密时边界层单元的耗散量较大,很小的 (可能非常接近0)无法保证其线性的生成项大于耗散项,导致出现负源项——这是正常的。但由于原始的S-A模型方程缺乏负源调节机制,即使只有一个单元出现负源,周围单元正的湍动能量会向其扩散导致自身净生成的减少引起负源扩散,最终使得全场运算的发散。一个简单修正的办法就是在计算中一旦出现负的时(负源已经产生并扩散),强制赋予一个很小的正数,相当于在后续的迭代中人为注入湍动能量,防止负源的扩散。
根据上面的讨论,下面对经典的RAE2882翼型跨声速流动算例进行计算。首先采用CFL3D网站发布的RAE2822标准网格,网格点分布为338×65,远场约为20倍弦长,第一层网格点到壁面距离约为1×10-5数量级。计算条件为[10]:
Ma=0.729,Re=6.5×106,α=2.79°
空间离散为三阶MUSCL的Vanleer格式,数值方法分为以下四种:
solver1: 5步Runge-kutta方法(CFL=0.3)+源项点隐式计算;
solver2: LU-SGS方法(CFL=5.0)+源项显式计算;
solver3: LU-SGS方法(CFL=5.0)+源项点隐式计算;
solver4: LU-SGS方法(CFL=5.0)+源项点隐式计算+ 修正。
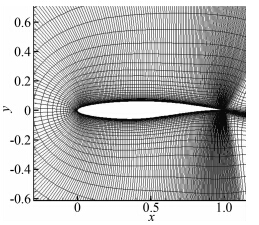 |
| 图 1 RAE2822翼型计算标准网格Fig. 1 Standard grid of RAE2822 |
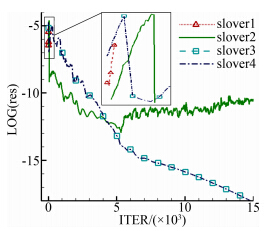 |
| 图 2 残值随迭代变化曲线(S-A模型,标准网格)Fig. 2 Residual VS number of iterations(S-A,standard grid) |
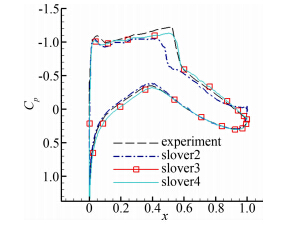 |
| 图 3 翼型表面压力系数分布曲线(S-A模型,标准网格)Fig. 3 Distribution of pressure coefficient(S-A,standard grid) |
从计算结果看出,CFL数取0.3时显式Runge-kutta方法仍不足以克服近似点隐式处理之后源项的残余刚性,计算很快发散,若一定采用这种方法只能进一步降低CFL数。由于LU-SGS方法自身的稳定性,即使源项显式计算(迭代方程中略去∂Q /∂W 项,源项显式计算在残差中)也能保证不发散,但残差高位震荡无法收敛,结果偏差很大。而solver3和solver4的计算结果完全一样,压力分布也与实验数据相差很小。这一方面说明了这种“双隐式”处理很好的模拟了流场,另一方面也说明在当前计算条件下 修正并未发挥作用,即并未出现负源扩散的现象。
考虑到很多分离问题要求对流动变量细微精确的捕捉,这时标准网格点分布显得较为稀疏。接下来对网格加密重新计算。新网格分布点为368×97,第一层网格点到壁面距离减小到1×10-6数量级,远场仍保 持20倍弦长,其余计算条件都不发生变化,计算结果显示除slover4外其余三组均无法收敛且其压力分布与标准网格几乎一致。进一步,图 7给出了距离翼型壁面最近的3层网格单元平均源项值的随迭代变化的情况。起初solver3和solver4每步平均源项值相同——其中可能有个别负源,但总体维持一个稳定状态。394步开始可能由于误差的扰动使得solver3算例中壁面附近大量产生负源并急剧扩散到全场,如图 8所示,之后10步即导致运算发散。而加入 修正的solver4算例不存在 类似问题,验证了 修正可以很好处理S-A模型在边界层密网格可能产生较大的源项刚性。同时这个算例也说明一味加密网格并不能简单促进控制方程对剧烈变化的湍动变量的捕捉,必须综合考虑各个因素对控制方程组的影响。
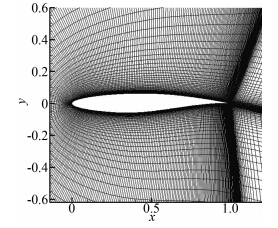 |
| 图 4 加密后的RAE2822网格Fig. 4 Fine grid of RAE2822 |
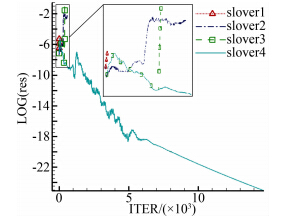 |
| 图 5 残值随迭代变化曲线(S-A模型,加密网格)Fig. 5 Residual VS number of iterations(S-A,fine grid) |
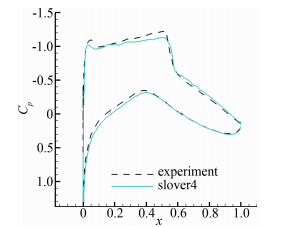 |
| 图 6 翼型表面压力系数分布曲线(S-A模型,加密网格)Fig. 6 Distribution ofpressure coefficient(S-A,fine grid) |
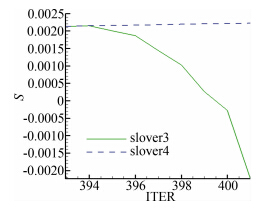 |
| 图 7 翼型附近平均源项值变化曲线(S-A模型) Fig. 7 Average of source term near the airfoil VS number of iterations(S-A) |
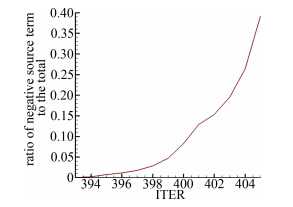 |
| 图 8 solver3负源单元占总单元数百分比变化曲线Fig. 8 Ratio of negative source term to the total vs. number of iterations in solver3(S-A) |
k-ω SST两方程模型是边界层内k-ω模型和远场k-ε模型的混合模型。该模型兼顾了两方面的优点:k-ω模型中的壁面衰减函数,对壁面附近湍流粘性系数预测较好;k-ε模型对来流条件不敏感,预测远场流动更为合适。其模型方程可以写为:
方程中常数的具体取值可参考文献[11]。相比S-A模型方程,k-ω SST模型方程源项要复杂得多。生成项和耗散项均为湍动的高度非线性函数,在ω方程中还增加了包含两个湍动变量导数的交叉输运项,这些不但大大提高了控制方程组的刚性,还导致精确求解源项整体的雅可比矩阵变得极为困难。为此需要将源项各部分分开考虑有针对性的进行处理。
类似对S-A模型方程的分析,由于k-ω SST模型的固壁边界条件为
其中d1为距壁面最近一层网格到壁面的距离。一般认为[12]不采用壁面函数k-ω SST模型壁面最近网格单元当地雷诺数y+<1,壁面网格很密,ω很大,直接导致模型方程耗散项很大,带来了很大的刚性。因此对于耗散项有必要采用下面的点隐式方法进行处理: 在生成项中,与S-A方程不同,即使壁面附近出现某个k<0也不会影响生成项τijSij的正定性,相反却可能出现湍动能过大的情况。一旦开始迭代时某单元出现负的湍动能k,雷诺应力τij偏大,生成项偏大,在两方程模型中边界层剪应力同生成项和耗散项之比的平方根成正比[7]导致剪应力偏大,一方面剪应力与湍动能的正相关性会很快将负的湍动能抹平,另一方面偏大的剪应力使得涡量偏大,也就是说生成项会继续增大,成为一个“正反馈”过程。而耗散项却没有一个类似的“机制”,最终湍动能无限增大计算崩溃。这也正是前面讨论的生成项和耗散项平衡问题,二者的差别不应超过一个数量级,否则不但影响边界层流动的模拟能力,更会带来计算稳定性等严重问题。为此可以将生成项修正为:
即k方程的生成项无论如何不超过其耗散项模的10倍。对于交叉输运项,其自身很大程度上也表示了生成和耗散之间的某种掺混关系,生成项修正后可直接显式计算。下面采用RAE2822翼型标准网格对SST k-ω模型进行算例验证,计算条件与S-A模型相同。数值方法分为下面三种:
solver1: LU-SGS方法(CFL =5.0)+耗散项点隐式式计算;
solver2: LU-SGS方法(CFL =5.0)+生成项修正;
solver3: LU-SGS方法(CFL =5.0)+耗散项点隐式式计算+生成项修正。
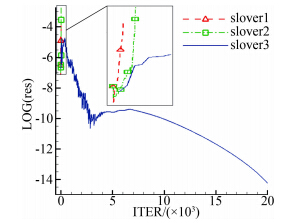 |
| 图 9 残值随迭代变化曲线(k-ω SST模型)Fig. 9 Residual vs. number of iterations(k-ω SST) |
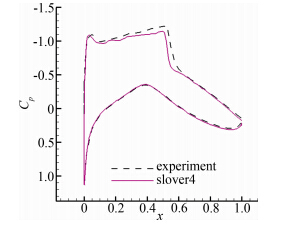 |
| 图 10 翼型表面压力系数分布曲线(k-ω SST模型)Fig. 10 Distribution of pressure coefficient(k-ω SST) |
从计算结果看出,只有solver3实现了较好的模拟,solver1和solver2都很快发散。这说明复杂的源项给k-ω SST模型控制方程组带来了很大的刚性,必须结合采用多种手段处理才能得到理想的结果。另外,同样是标准网格算例,k-ω SST模型收敛速度明显较S-A模型慢,这也佐证了由于刚性较大而导致的局部时间步长进一步减小的结论。 4 结 论
本文以S-A一方程模型和k-ω SST两方程模型为例,研究了湍流模型方程源项对控制方程组产生的影响以及在实际应用中的求解办法。源项对原控制方程组双曲性态的影响使得湍流变量在时间尺度和空间尺度的剧烈变化,带来了严重的数值刚性问题。对此除了将源项和时间导数项耦合点隐式处理这一常规思路外,必须综合考虑生成项和耗散项之间的平衡关系(特别是在边界层中),防止迭代误差导致过大或过小的源项值的扩散——这需要从流动物理机制出发,对不同湍流模型源项做不同的分析处理。数值验证结果显示无论是对源项刚度较小的S-A模型还是较大的k-ω SST模型,在有针对性的源项处理后都得到了良好的收敛效果。
| [1] | YAN C. Methods and applications of computational fluid dymanics[M]. Beijing: Beihang University Press, 2006. (in Chinese)阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006. |
| [2] | LI X L, FU D X, MA Y W. Direct numerical simulation of hypersonic boundary layer transition over a blunt cone[J]. AIAA Journal, 2008, 46(11): 2899-2913. |
| [3] | HUANG P G, COAKLEY T J. An implicit Navier-Stokes code for turbulent flow modeling[R]. AIAA 92-0547. |
| [4] | BLAZEK J. Computational fluid dynamics: principles and applications[M]. London: ELSEVIER Science Ltd, 2001. |
| [5] | DU T, WU Z N. Mixed analytical/numerical method for low Reynolds-number k-w epsilon turbulence models[J]. AIAA Journal, 2004, 42: 1140-1153. |
| [6] | DU T, WU Z N. Mixed analytical/numerical method applied to the high Reynolds number κ-ε turbulence model[J]. Computers & Fluids, 2005, 34(1): 97-119. |
| [7] | DU T, WU Z N. Mixed analytical/numerical method for flow equations with a source term[J]. Computers & Fluids, 2003, 32(5): 659-690. |
| [8] | DU T, YANG Y, WU Z N.Mixed analytical/numerical method and its application to problems of turbulent flow simulation[J]. Acta Aeronautica Et Astronautica Sinica, 2007, 27(2), 198-203. (in Chinese)杜涛, 杨勇, 吴子牛. 混合解析/数值方法及其在湍流数值模拟上的应用[J]. 航空学报, 2007, 27(2): 198-203. |
| [9] | SPALART P R, ALLMARAS S R. A one-equation turbulence model for aerodynamic flows[R]. AIAA 920439. |
| [10] | COOK P H, MCDONALD M A, FIRMIN M C. Aerofoil RAE 2822 pressure distributions, and boundary layer and wake measurements[R]. Experimental Data Base for Computer Program Assessment, AGARD AR 138, 1979. |
| [11] | MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. |
| [12] | MERCI B, STEELANT J, VIERENDEELS J. Computational treatment of source terms in two-equation turbulence models[J]. AIAA Journal, 2000, 38(11): 2085-2093. |