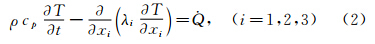随着新一代高超声速飞行器的发展,防热设计遭遇了更为严峻的挑战。一方面是飞行器要面临高焓、中低热流和长时间气动加热的恶劣热环境;另一方面是要在满足极为苛刻的质量要求下实现非烧蚀防热。为了能够更合理的选材和优化防热,以便进一步减小设计冗余,这就对飞行器热环境的准确预测提出了更高的要求。
新一代高超声速飞行器的热环境特性与其自身气动外形、所处飞行环境及其内部结构形式和材料物理属性等密切相关,外部流场的气动加热与内部结构热响应之间存在强烈的耦合关系。因此,必须研究和建立基于流场、热、结构多场耦合的飞行器热环境数值分析方法和手段。
关于流场、热、结构多场耦合基础问题的研究,国外开展得较早。Thornton和Dechaumphai等人[1, 2, 3]于20世纪80年末首次提出流场、热、结构多场耦合问题,并对多场耦合特征和关键问题进行了初步计算分析。Chen等人[4, 5, 6]通过松耦合的方式对流场和结构进行迭代求解,率先将多场耦合计算方法应用于航天领域。20世纪初,国内学者黄唐、毛国良等人[7]率先研究了二维流场、热、结构一体化数值模拟方法。此后国内一些学者陆续开展了流场、热、结构多场耦合计算研究和分析[8, 9, 10, 11, 12]。但总体而言,国内还主要侧重于稳态飞行环境下的流场、热、结构多场耦合基础问题的理论方法研究。对于飞行器实际热环境的准确预测,还需要进行非稳态飞行环境下的流场、热、结构多场耦合分析,而这方面研究相对较少,对其多场耦合规律和特征的认识还不够深入,相关分析方法和研究手段还有待进一步发展和完善。
通过对飞行器热环境多场耦合特性的分析,提出了一种基于多场耦合的热环境数值分析策略,并在此基础上建立了相应的基于流场与结构耦合传热的飞行器热环境多场耦合数值分析方法。以典型圆管前缘为计算模型进行了程序验证,并对稳态和非稳态飞行环境下的流场与结构耦合传热特征和规律进行了数值分析研究。 1 问题分析及耦合分析策略
高超声速飞行器在实际飞行过程中所经历的是 一个沿特定飞行轨迹变化的持续、非瞬态的受热过 程,其物理实质是一个在长时间持续非稳态飞行环境下的流场、热、结构多场耦合问题。
上述问题涉及到多个时间尺度,由于飞行器外部飞行环境的变化是其刚性整体宏观运动行为且时间跨度较大,故飞行器飞行环境随时间的变化一般情况下相对较为缓慢,因而其对外部流场特性产生影响的特征时间尺度会远大于流场、热、结构之间发生耦合效应的特征时间尺度。基于上述实际,本文提出如图 1所示的基于多场耦合的热环境数值分析策略。具体内容为:1)将飞行器整个飞行轨迹视为时域内连续变化的飞行环境状态函数,即可表述为FS=f(H,Ma,α,t);2)根据飞行环境状态函数变化特征和计算精度要求,选取合适的时间步长Δttr将其在时域内进行离散,划分为一系列的离散飞行状态点(H,Ma,α)i,其中每个离散飞行状态点的持续时间为Δttr,其内飞行条件恒定且取该状态点起始时刻和终止时刻飞行条件的平均,这样就将长时间持续非稳态飞行环境下的多场耦合问题转化为有限个准稳态飞行环境下的多场耦合问题的集合;3)在每个离散飞行状态点内,可根据多场耦合特征和计算精度要求,选取合适的耦合计算时间步长Δtcp= 1 n ·Δttr进行耦合计算。在完成一个离散飞行状态点内的耦合计算后,按照时间序列转入下一个离散飞行状态点内继续计算直至飞行时间结束。
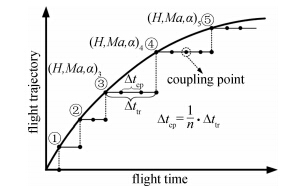 |
| 图 1 基于多场耦合的热环境数值分析策略Fig. 1 Multi-field coupling numerical analysis strategy for predicting aerothermal environment |
下面进一步分析稳态环境下的流场、热、结构多场耦合问题。对于新一代高超声速飞行器防热设计,由于要保持良好的气动外形,不允许结构有较大变形。本文暂不考虑结构变形的影响,假定结构为刚性体,这样可简化为流场与结构耦合传热问题。
对于流场与结构耦合传热问题,通常可采用两类方式求解:1) 整体求解方式;2) 分区迭代方式。其中,分区迭代方式是指各场分别采用各自的求解器在时域内依次交替时间步进行推进求解,耦合作用通过界面传递耦合变量实现。这种方式可以充分利用各场特点和成熟算法,易于实现和模块化,因而得到广泛应用。因此,本文采用分区迭代方式。
对于高速可压缩流动,流场被扰动后重新达到稳定的特征时间一般为毫秒量级,而结构传热的特征时间一般为秒量级。若采用分区迭代方式求解流场与结构传热问题时,以流场计算时间步长作为耦合时间步长,将导致极大的计算量。研究表明,即使边界处热流很大,壁面温度在较短时间内变化也不是很大,其对流场的影响也仅限于附面层极小范围内,故与结构传热计算时间步长相比,可认为流场是瞬时稳定的[9]。基于上述实际,采用如图 2所示的流场与结构耦合传热分区迭代求解策略。
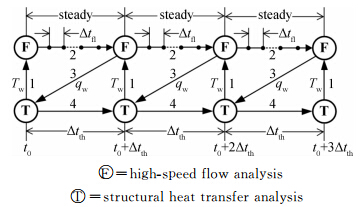 |
| 图 2 流场与结构耦合传热分区迭代求解策略Fig. 2 Partitioned iteration strategy of the flow-structural coupling heat transfer |
具体步骤为:1) 根据初始时刻t0的结构热分析结果,通过耦合界面向流场提供壁面温度边界条件Tw;2) 根据壁面温度边界条件Tw,计算定常流场得到壁面气动热流密度qw;3) 通过耦合界面将壁面气动热流密度qw传给结构,为热分析提供热流密度边界条件;4) 根据壁面热流密度边界条件qw,在t0至t0+Δtth时间段内进行瞬态传热分析,得到t0+Δtth时刻的结构温度场分布,至此完成一个耦合计算时间步长Δtth内的迭代计算。 2 控制方程及数值方法 2.1 流场
考虑基于量热完全气体模型的三维粘性可压缩流动Navier-Stokes方程,其在笛卡尔坐标系下的守恒积分形式为:
式中: Q为流场守恒向量;F c和 F ν分别为对流矢通量和粘性矢通量。本文基于有限体积法对上述控制方程进行离散求解。其中,对流通量采用M-AUSMPW+混合迎风格式[13]进行离散,并用多维限制器MLP[14]提高至三阶精度;粘性通量采用二阶中心差分格式进行离散;时间推进采用LU-SGS隐式方法[15]。为了加速收敛过程,采用当地时间步长和隐式残值平均等加速收敛措施。 2.2 结构温度场
固体结构内部温度场的控制方程为导热微分方程。在笛卡尔直角坐标系下,三维非稳态导热微分方程的表达式为:
式中:t为时间;T为温度;ρ为材料密度;cp为材料比热 容;λi为材料的热传导系数;Q犙为固体内部的热源密度。对于上述结构温度场控制方程,本文直接采用商用有限元热分析软件ANSYS作为求解器进行离散求解。 2.3 界面耦合关系及数据传递
流场与结构耦合传热的实质是流场和结构温度场通过飞行器壁面发生耦合作用。如图 3所示,设Ωf和Ωs分别为流体域和固体域,Гfs=Ωf∩Ωs为耦合界面,则在耦合界面Гfs处满足如下关系:
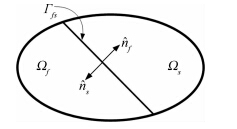 |
| 图 3 流体域与固体域耦合关系示意图Fig. 3 Schematic illustration of thecoupling relationship between fluid and solid domains |
对于上述耦合关系,采用Dirichlet-Neumann方法处理[16],即固体域向流体域提供壁面温度条件,而流体域向固体域提供热流密度边界条件。
由于流体域和固体域分别采用了不同的离散方法和数值格式,在耦合界面上存在两套非匹配网格之间的数据传递,这在数学上是一个双向插值问题,本文主?捎肧hepard方法[17]来实现。该方法首先由气象学家与地质工作者提出,其基本思想是将待插值点的函数值定义为已知数据点的函数值的距离倒数加权之和:
式中:M为待插值点的函数值;Mi为已知数据点的函数值;di为待插值点与已知数据点之间的欧氏距离;n为已知数据点的个数;p为距离的幂次,其值越高插值结果越光滑。 3 计算结果及分析 3.1 计算模型及初场验证高超声速飞行器头部通常采用钝体前缘设计,故这里选取二维圆管前缘[10, 18]作为计算模型。该圆管前缘的内外半径尺寸以及所采用的计算网格如图 4所示。其中,固体域采用有限元网格划分,最小单元边长为0.5mm;流体域采用结构化网格划分,网格大小为201×111,且在激波和近壁面附近进行了加密处理。圆管内部结构材料为不锈钢,初始壁面温度及外部流场的来流参数如表1所示。
 |
| 图 4 计算模型及计算网格Fig. 4 Computational model and computational mesh |
图 5所示为初始时刻t=0s时外部流场温度云图以及沿驻点线温度分布。可以看出,计算得到的温度场分布宏观上符合物理实际,其中最大温度值与理论总温一致,流场激波位置与理论位置相符,沿驻点线温度分布符合正激波前后物理关系。
 |
| 图 5 初始时刻t=0s时温度场分布Fig. 5 Initial temperature field distribution at t=0s |
为了考察壁面热流计算的准确性,以文献[19]提出的准则为依据确定壁面法向网格尺度。图 6给出了初始时刻t=0s时归一化的壁面热流密度分布与试验结果的对比,可以看出计算结果与试验结果符合得较好。
 |
| 图 6 计算与试验的壁面热流分布对比Fig. 6 Comparison of wall heat-flux distribution between the computation and the experiment |
首先考察了耦合计算时间步长对壁面温度的影响情况,如图 7所示,总的持续时间为5s。可以看出,当耦合计算时间步长为5s时,即热载荷一次加载,不存在耦合作用,计算得到的壁面温度最高;随着耦合计算时间步长的减小,即耦合次数的增多,计算的壁面温度越低。这表明,充分考虑了流场与结构耦合传热效应后,对结构温度的预测更接近实际物理过程,可以进一步减小由于结构温度高估而引起的设计冗余,且这种效果会在气动加热越剧烈的地方越明显,利于更合理地选材和进行优化设计。
 |
| 图 7 不同耦合时间步长对壁面温度的影响Fig. 7 Effects of different coupling computational time step on the predicted wall temperature |
从图 7还可以看出,随着耦合计算时间步长的减 小,其对壁面温度的影响也逐渐减少,当耦合计算时间步长减小至一定程度后,壁面温度的变化已经不再明显。这表明,随着耦合计算时间步长的减少,计算精度逐渐增加,流场与结构之间的耦合传热逐渐接近实际的物理过程。
图 8给出了采用耦合计算时间步长为Δt=0.5s时的壁面温度分布随时间的变化情况。随着时间的持续,壁面温度从初始时刻的分布逐渐上升,其变化过程符合物理实际,最终t=5s时刻的壁面温度分布量值上略低于试验结果,但分布规律趋势与试验结果相一致。
 |
| 图 8 壁面温度分布随时间的变化Fig. 8 of wall temperature distribution with the time |
为了进一步考察长时间持续飞行对热环境特性的影响,这里将总的持续飞行时间延长至50s,采用耦合计算时间步长为0.5s,进一步进行了分析。
图 9和图 10分别给出了壁面驻点处温度、气动加热热流及它们的时间导数随长时间持续的变化情况。随着飞行时间的持续,结构的温度将会不断地上升,其温度变化率在起始时刻变化比较剧烈,但随着时间的持续,增幅将逐渐减小并渐趋于零;相对于结构温度的变化,壁面热流密度随着时间的持续会不断地下降,其降幅也不断减小。由此可以进一步推知,随着飞行时间的持续,流场与结构之间的耦合传热最终将会达到一个动态平衡状态。通过上述分析可知, 对于长时间持续飞行,即使马赫数不是很高,结构温度也可能达到很高的值,飞行器防热设计必须考虑飞行时间的累积效应。
 |
| 图 9 驻点处温度及其时间导数随长时间持续变化Fig. 9 Long-duration variation of the temperature and its time derivative at stagnation point |
 |
| 图 10 驻点处热流及其时间导数随长时间持续变化Fig. 10 Long-duration variation of the heat-flux and its time derivative at stagnation point |
图 11给出了外部流场和内部结构沿驻点线温度分布随长时间持续变化情况。可以直观看出,外部流场的变化仅限在边界层近壁处极小范围内,流场温度与结构内部温度在壁面处连续,外部流场气动加热通过壁面逐渐向结构内部传递,随着时间的持续,结构内部温度逐渐增加。图 12给出了t=50s时外部流场和结构内部温度分布云图,可以直观地看出结构内部传热具有明显的多维特征,热量除了主要沿壁面法向传递外,还会向其它方向传递。
 |
| 图 11 流场及结构沿驻点线温度分布随长时间持续变化Fig. 11 Long-duration variation of the temperature within the fluid and structure along stagnation line |
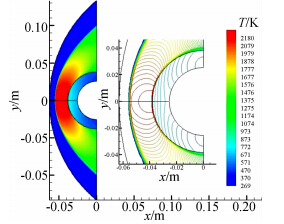 |
| 图 12 在t=50s时流场及结构内部温度分布Fig. 12 Temperature distribution within the fluid and structure at t=50s |
高超声速飞行器在实际飞行过程中一般会经历上升、巡航和下降等状态。本文暂未考虑攻角的变化,根据气动载荷限制条件给出了一条简单的典型飞 行轨迹,如图 13所示,总的持续飞行时间为410s,其中:上升时间为0~50s,巡航时间为50s~350s,下降时间为350s~410s。这里选取时间步长Δttr=5s将飞行轨迹离散划分为82个离散飞行状态点。对于本 次计算,流场与结构耦合传热的计算时间步长取为 Δtcp=Δttr=5s;圆管前缘的材料采用C/C复合材料, 其初始时刻的温度为288.15K。
 |
| 图 13 飞行轨迹及其离散划分Fig. 13 Flight trajectory and its discretization |
图 14给出了来流总焓、圆管前缘驻点壁面温度、气动加热热流沿飞行轨迹的分布。可以看出:(1)从起始时刻t=0s至巡航状态t=50s开始,结构壁面温度逐渐上升,但同时由于飞行速度的逐渐增大,流场的气动加热能力逐渐增强,气动加热热流密度并没有降低,而是随之逐渐增大。在这一过程中,通过耦合界面传入结构内部的气动加热量越来越多,结构处于不断储能的状态。(2)在巡航状态t=50s~350s,虽然飞行条件不再变化,流场的气动加热能力恒定,但由于流场与结构之间的耦合传热作用,不断有气动加热量持续地传入结构内部,导致结构壁面温度会继续上升,传入结构内部的气动加热量越来越小,气动加热热流密度开始逐渐下降,但结构仍处于储能状态。如果巡航时间足够长,随着结构内部热能的不断储存,最终流场与结构之间的耦合传热将达到一个动态平衡状态。(3)进入下降状态t=350s~410s,飞行速度开始降低,流场气动加热能力开始减弱,此时结构温度已经很高,气动热流密度会继续下降,外部气动环境难以再继续保持结构的储能状态,结构开始转为释能状态,结构内部的热能开始向外传递,从而结构壁面温度开始逐渐下降。
 |
| 图 14 来流总焓、驻点温度和热流密度沿飞行轨迹的分布Fig. 14 Distribution of the fluid’s total enthalpy,temperature and heat-flux at the stagnation point along trajectory |
图 15给出了结构内部温度场沿飞行轨迹的分布,从中可以直观看出结构内部温度分布及热能传递方向随飞行轨迹的变化规律。由于流场与结构之间的耦合传热效应,起初外部气动环境使热能不断向结构内部传递,当外部气动环境难以维持结构的储能状态时,结构内部热能转而向外传递。能够准确地预测和分析热在结构内部的时空分布和传递规律,进而加以引导和控制,这对于新型防热概念及方法的研究具有重要的意义。
 |
| 图 15 结构内部温度场沿飞行轨迹的分布Fig. 15 Distribution of the temperature field within the structure along trajectory |
通过对飞行器热环境多场耦合特性的分析,提出了一种基于多场耦合的热环境数值分析策略,建立了相应的数值分析方法。以典型圆管前缘为计算模型,对稳态和非稳态飞行环境下的热环境特性进行了数值分析研究。结果分析表明:
(1) 充分考虑流场与结构之间的耦合传热效应,对结构温度的预测更接近物理实际,可以进一步减小设计冗余,而且这种效果会在气动加热越严重的地方越明显;
(2) 对于长时间持续飞行,在稳态飞行环境下,即使马赫数不是很高,结构温度也可能达到很高的值,流场与结构之间的耦合传热最终将达到一个动态平衡状态;在非稳态飞行环境下,外部流场气动加热能力的变化,会改变结构内部热能的分布和传递,引起热流峰值或温度峰值,飞行器热环境随飞行轨迹变化表现出动态的多场耦合时空特性。
综合以上分析,本文提出的基于多场耦合的飞行器热环境数值分析策略以及所建立的数值分析方法,能够有效地刻画流场与结构之间的耦合传热特征和规律,预测和分析飞行器热环境空间和时间分布特性,可为防热设计的选材和优化提供可靠的参考依据和分析手段。同时值得指出的是,由于本文重点在于数值分析策略和方法的研究,暂未考虑壁面辐射特性的影响。实际上飞行器壁面辐射特性对气动热环境具有重要的影响,且随着飞行时间的持续而不断加强,有待进一步的分析和研究。
| [1] | THORNTON E A, DECHAUMPHAI P. Coupled flow, thermal and structural analysis of aerodynamically heated panels[J]. Journal of Aircraft, 1988, 25(11):1052-1059.doi: 10.2514/3.45702 |
| [2] | DECHAUMPHAI P, THORNTON E A, WIETING A R. Flow-thermal-structural study of aerodynamically heated leading edges[J]. Journal of Spacecraft,1989, 26(4):201-209. |
| [3] | DECHAUMPHAI P, WIETING A R, PANDEY A K. Fluid-thermal-structural interaction of aerodynamically heated leading edges[R]. AIAA 89 1277, 1989. doi: 10.2514/6.1989-1227 |
| [4] | CHEN Y K, HENLINE W D, TAUBER M E. Mars pathfinder trajectory based heating and ablation calculations[J]. Journal of Spacecraft and Rockets, 1995, 32(2):225-230. |
| [5] | CHEN Y K, MILOS F S. Solution strategy for thermal response of non-ablating thermal protection systems at hypersonic speeds[R]. AIAA 1996-0601.doi: 10.2514/6.1996-615 |
| [6] | CHEN Y K, MILOS F S.Two-dimensional implicit thermal response and ablation program for charring materials on hypersonic space vehicles[R]. AIAA 2000-0206. doi: 10.2514/6.2000-206 |
| [7] | HUANG T, MAO G L, JANG G Q, et al. Two dimensional coupled flow-thermal-structural numerical simulation[J]. ACTA Aerodynamica Sinica, 2000, 18(1): 115-119. (in Chinese)黄唐, 毛国良, 姜贵庆, 等. 二维流场、热、结构一体化数值模拟[J]. 空气动力学学报, 2000, 18(1): 115-119. |
| [8] | GUI Y W, YUAN X J. Numerical simulation on the coupling phenomena of aerodynamic heating with thermal response in the region of the leading edge[J]. Journal of Engineering Thermophysics, 2002, 23(6):733-735. (in Chinese)桂业伟, 袁湘江. 类前缘防热层流场与热响应耦合计算研究[J]. 工程热物理学报, 2002, 23(6): 733-735. |
| [9] | XIA G, LIU X J, CHENG W K, et al. Numerical simulation of coupled aeroheating and solid heat penetration for a hypersonic blunt body[J]. Journal of National University of Defense Technology, 2003, 25(1):35-39. (in Chinese)夏刚, 刘新建, 程文科, 等. 钝体高超声速气动加热与结构热传递耦合的数值计算[J]. 国防科技大学学报, 2003, 25(1): 35-39. |
| [10] | ZHAO X L, SUN Z X, TANG L S, et al. Coupledflow-thermal-structural analysis of hypersonic aerodynamically heated cylindrical leading edge[J]. Engineering Applications of Computational Fluid Mechanics, 2011, 5(2):170-179. |
| [11] | NIE T, LIU W Q. Study of coupled fluid and solid for a hypersonic leading edge[J]. ACTA Phys. Sin., 2012, 61(18): 184401-1-184401-7. (in Chinese)聂涛, 刘伟强. 高超声速飞行器前缘流固耦合计算方法研究[J]. 物理学报, 2012, 61(18): 184401-1- 184401-7. |
| [12] | LI X, ZHANG J F, HE Y L, et al. Numerical analysis of two-dimensional fluid/thermal structure loosely-coupled simulation[J].Journal of Engineering Thermophysics, 2012, 33(1): 87-90. (in Chinese)李欣, 张剑飞, 何雅玲, 等. 二维流场、热结构松耦合模拟研究[J]. 工程热物理学报, 2012, 33(1):87-90. |
| [13] | KIM K H, KIM C. Accurate, efficient and monotonic numerical methods for multi-dimensional compressible flows part I: spatial discretization[J]. Journal of Computational Physics, 2005, 28(2): 527- 569. doi:10.1016/j.jcp.2005.02.021 |
| [14] | YOON S H, KIM C, KIM K H. Multi-dimensional limiting process for three-dimensional flow physics analyses[J]. Journal of Computational Physics, 2008, 227: 6001-6043. doi:10.1016/j.jcp.2008.02.012 |
| [15] | YOON S, JAMESON A. Lower-upper symmetry gauss-seidel method for the Euler and Navier-stokes equations[J]. AIAA Journal, 1988, 26(9): 1025-1026. doi:10.2514/3.10007 |
| [16] | GILES M. Stability analysis of numerical interface conditions in fluid-structure thermal analysis[J].International Journal of Numerical Methods in Fluids, 1997, 25(4):421-436. doi:10.1002/(SICI)1097-0363(19970830)25:4<421:AID-FLD557>3.0.CO;2-J. |
| [17] | SHEPARD D. A two dimensional interpolation function for irregularly spaced data[C]. Proceedings of 23rd National Conference of the Association for Computing Machinery, New York, 1968:517-524. |
| [18] | WIETING A R. Experimental study of shock wave interference heating on a cylindrical leading edge[R]. NASA TM100484, 1987. |
| [19] | CHENG X L, AI B C, WANG Q. A wall grid scale criterion based on the molecule mean free path for the wall heat flux computations by the Navier-Stokes equations [J].Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(6):1083-1089.(in Chinese)程晓丽, 艾邦成, 王强. 基于分子平均自由程的热流计算壁面网格准则[J]. 力学学报,2010, 42(6):1083-1089. |