增升装置的设计是为了在大型客机起飞和降落阶段获得足够的升力系数,但是其常伴随产生高强度的气动噪声。越来越严格的国际噪声控制标准[1],使得大型客机的噪声及其降噪方法成为当前的一个研究热点。风洞实验[2, 3, 4]和飞行测试[5]均表明,缝翼噪声是大型客机起降时机体噪声的主要成分之一。因此,开展缝翼噪声的降噪技术研究,阐述其主要降噪机理,可为工程实践提供指导,进而有效地降低客机的总体噪声水平。
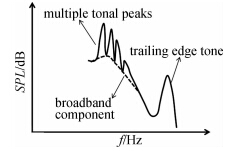
如图 1所示,缝翼噪声包括三种典型成分,即宽频噪声,低频窄带噪声和高频窄带噪声[2]。其中,宽频噪声被认为与剪切层与缝翼压力面的撞击有关,宽频噪声频率范围为St≈1~3(斯德鲁哈尔数St≈fcslat/u∞,f为噪声频率,u∞为远场来流速度,cslat为缝翼弦长)。高频的窄带噪声由缝翼尾缘脱落的涡产生,低频窄带成分源于一种涡声耦合自励反馈机理,其仅在特定的攻角、缝道宽度/缝道重叠量的等比例缩小风洞实验模型上出现,被认为与缝翼尖端处拟序的层流分离有关[6]。低频窄带噪声致声机理如图 2所示,从尖端拖出去的涡被剪切层裹挟而往下游发展,与缝翼尾缘撞击后,产生一压力波,其在空腔内部往尖端处传播,最终在尖端处诱发新生剪切层的不稳定性,形成一自我激励机制。
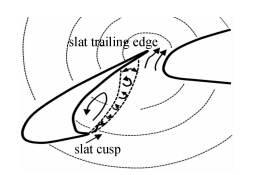 |
| 图 2 低频窄带噪声致声机理Fig. 2 Mechanism of the low-frequency tonal noise |
客机在实际飞行中,缝翼尾缘厚度与弦长的比值较风洞模型相应的比值要小得多,因此,导致高频噪声的钝体尾缘涡脱落现象在实际构型上并不显著,缝翼高频噪声比低频噪声要微弱的多[7],同时人耳对低频段(约2kHz)噪声更为敏感,因此本文更多的关注于低频噪声。
为抑制缝翼低频噪声,国内外学者广泛开展了主/被动噪声控制方面的研究。在被动控制技术上,缝翼空腔遮蔽[4]、缝翼密封片[8]和缝翼填充物[9]通过遮蔽部分回流区或完全消除回流区而推迟或消除了剪切层的形成,从而在根本上抑制或消除了声产生机制。锯齿状缝翼尖端[10]则加剧了缝翼的展向流动,打碎了从缝翼尖端脱出去的大涡,减小了涡与缝翼碰撞所产生的压力脉动。这些被动控制方法在缝翼降噪上 具有较好的效果。例如,缝翼空腔遮蔽在0~10kHz 范围内能够降低2dB的缝翼噪声。
由于被动控制技术常在非设计工况下不能达到预期的噪声抑制效果,国内外学者们积极开展缝翼噪声主动控制研究。在主动控制上,Knacke[11]等通过在缝翼空腔布置多重吸气槽来抽离回流气泡,显著降低了缝翼的噪声;Wells[12]在缝翼靠近尾缘的压力面往外喷气,以期将不稳定流吹离壁面来降低剪切层与固壁的撞击,由于喷口靠近缝道宽度出口区,从该处射流的能量不足以将高速的不稳定流吹离壁面,该尝试没有成功。Chen[13]在缝翼尖端附近布置介质阻挡放电(Dielectric Barrier Discharge,DBD )等离子体激励器来降低缝翼窄带噪声,其认为等离子体激励器降低噪声的潜在的三种机理为:1) 等离子体类似声衬的作用,可以削弱声朝地面的反射;2) 等离子体诱导流消除或降低了缝翼尾迹的不稳定性;3) 等离子体的安装填充了部分的空腔,从而减小了回流气泡的尺寸。
为了降低缝翼的低频噪声,本文提出一种在缝翼前缘施加平行喷流的主动控制技术。缝翼的几何结构与空腔类似,在空腔噪声控制上,喷流是一种主动可调的流动控制技术,具有较成熟的应用[14, 15, 16, 17]。射流降噪的机理为射流加厚了边界层,从而增加了边界层的稳定性,其可以减轻甚至消除剪切层与下游角区的撞击。在基于定常喷流的凹坑噪声控制中,有在前缘角区的上游垂直于远场来流方向向上射流[14, 15],以及在前缘角区低于角区高度的壁面平行于远场来流方向射流[16]和与远场来流成45°角斜向上射流[17]。
在空腔射流方向的选择上,当射流具有垂直于远场来流的分量时,剪切层会往空腔外部移动,对应于缝翼这一特殊的空腔构型,即为剪切层发展到尾缘后较基准构型会往主翼方向偏移,从而“堵塞”部分通道,此时流过缝道区的流量不可避免的会减小。由于缝翼增升机理为与主翼构成一收缩通道,通过缝道区的高速流体吹除主翼吸力面的剪切层,加速主翼吸力面上的流动和延缓失速,当通过缝道区域的流量减小时,会降低增升装置的增升性能。基于上述考虑,本文选择了在平行于远场来流的方向上喷流。
为了降低缝翼的低频噪声,本文在上述工作的基础上,引入已成熟应用在空腔的射流降噪技术,同时为了保持缝翼的增升性能,选择在缝翼尖端附近平行射流。数值模拟了平行射流在缝翼降噪上的应用;得到了与实验结果基本一致的表面压力分布、空腔速度分布和中场监测点的噪声频谱,同时分析了射流对缝翼气动力和气动噪声的影响,并分析了其降噪机理。 1 数值计算方法 1.1 缝翼模型
基准构型采用德国FRENQUENZ项目[3]采用 的两段构型,该构型包括缝翼和主翼基准构型对应 的声风洞实验条件为:巡航构型弦长cstowed=0.4m,马赫数M=16,攻角α=13°,对应于巡航构型弦长的雷诺数Re=1.4×106。
射流构型如图 3所示,射流缝宽h=1.6mm,假定在整个缝宽上速度为均匀分布,缝下游边缘距尖端距离为1.2mm。采用了两组射流量,射流速度uslot分别为30m/s和45m/s,射流方向平行于从缝翼尖端指向缝翼尾缘的矢量方向。对应的无量纲动量系数cμ=2h/cstowed(uslot/u∞/)2分别为2.43×10-3和5.47×10-3。
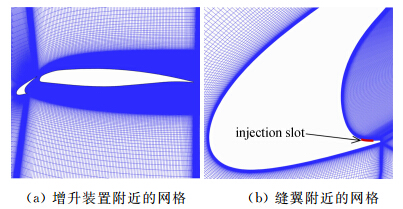 |
| 图 3 计算网格Fig. 3 Computational grids |
采用二维模拟,网格数为70万。为了准确捕捉缝翼空腔内非定常流动,其中25万网格点位于空腔。边界层划分了26个点,第一层网格相对于巡航构型弦长的无量纲高度为1.71×10-5,对应的y+≈1。远场为C型边界,外边界距主翼前缘为50倍巡航翼型弦长。 1.3 数值方法
基于商用软件FLUENT 14.0,采用基于SST k-ω湍流模型的延迟脱体涡模拟(Delayed Detached Eddy Simulation,DES)来计算声源,再利用FLUENT内置 的FW-H积分模块获得远场的噪声特性,空间和时间离散精度都为二阶。非定常模拟中,采用20步亚迭代来加速收敛。DES特别适用于计算分离流:RANS可以有效地模拟边界层,且计算资源比LES小得多; 在边界层外,LES直接模拟大尺度涡,小尺度涡对大涡的影响通过亚格子模型来近似模拟。DES可以在整个流场上既满足计算精度要求又节省计算成本,DDES较DES可以在边界层模拟上隔绝LES的侵扰,从而可以划分更为细密的网格,提高了能够模拟的最高频率[18]。
为了降低缝翼空腔的涡粘性,使缝翼空腔流动的非定常特性充分发展,采用DDES模拟声源。由于是二维模拟,忽略了涡的展向特性,没有考虑到涡轴指向的改变和涡的三维延伸机制[11]。由于本文的目的为探讨射流在缝翼降噪上的应用及其机理,而不是进行定量的降噪研究,所以采用二维DDES模拟。
在时间推进的处理上,将RANS解作为非稳态推进解的初始值,然后推进4000步以获得准稳态解,接下来的7000步流场数据用于做统计分析以获得远场噪声特性。无量纲时间步长Δ/tu∞/cstowed=1.496×10-3,此时远场来流流过巡航构型弦长的距离需要668步。将每一迭代步获得的缝翼和主翼固壁上的声源信息进行FW-H积分,以获得远场噪声特性。针对增升装置,固壁积分面和可穿透面积分所获得的远场噪声特性在机翼下方指向上基本一致[19],所以本文只采用了固壁积分。 2 计算方法的验证 2.1 表面压力系数
为了验证数值方法在模拟增升装置气动特性上的能力,将无射流情况下的DDES计算得到的表面压力系数时均值与风洞实验值进行了对比,如图 4所示,计算得到的表面压力系数分布与风洞实验值基本一致。
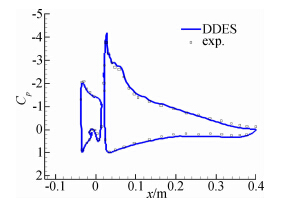 |
| 图 4 表面压力系数Fig. 4 Coefficient of surface pressure |
缝翼低频噪声由剪切层与缝翼固壁的撞击所产生,因此,剪切层发展的模拟对噪声计算的准确度影响很大。为了验证计算方法在模拟剪切层发展上的准确度,在空腔区域监测了四条线上的速度分布,并与风洞实验值进行了对比,四条线的几何位置如图 5所示,图 6为DDES计算得到的垂直于监测线的速度分量时均量沿线的分布,横坐标为无量纲化的沿监测线的距离,纵坐标为用远场来流声速无量钢化的速 度。与Konig等[20]所获得的对比结果类似,线B、线 C在靠近缝翼固壁的一端数值解与实验值差别较大,这是由于PIV实验在空腔靠近固壁的回流区撒布的粒子较少,所获得的实验数据不准确导致的。四条线上的速度分布外形、速度大小与实验值符合较好,即准确地模拟了剪切层的发展。
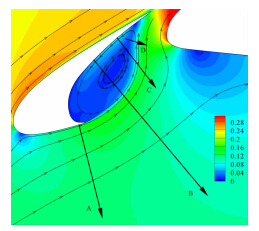 |
| 图 5 空腔区域监测线的几何位置示意图Fig. 5 Location of survey lines |
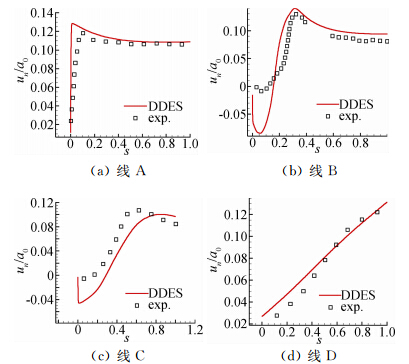 |
| 图 6 垂直于监测线的速度分量时均量沿监测线的分布Fig. 6 Velocity distributions normal to the lines as a function of the normalized coordinates along lines |
在中场设置了两个监测点并将其噪声频谱与风 洞实验值进行了对比,两个监测点的位置如表 1所示。如图 7所示,坐标原点位于主翼前缘,角度按逆时针方向增长。在FW-H积分的处理上,将声源信息分为六段,相邻两段声源信息的重叠量为50%,然后将六段声源信息积分得到的中场噪声能量谱密度进行平均。
 |
| 图 7 中场监测点示意图Fig. 7 Definition of the microphone positions |
风洞实验数据表明,中场监测点P1和P2的噪声能量谱密度具有四个峰值[3],近似的有f1=1230Hz,f2=1915Hz,f3=2560Hz,f4=3280Hz。从图 8可知,第二、三、四个峰值在峰值频率上与实验 值符合一致,在幅值上较实验值要小,第一个峰值没有捕捉准确,这应该是由于忽略展向效应,没有全面 捕捉到空腔的涡动力学行为所引起的。从监测点的能量谱密度可知,二维情况下的噪声数值模拟具有合适的精度,捕捉到了主要的发声机理。
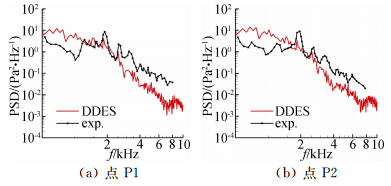 |
| 图 8 中场监测点的噪声能量谱密度Fig. 8 Sound spectra at the near far-field locations |
首先,为了确保增升装置的增升性能没有受到影响,对升/阻力系数进行了比较;接下来比较了三种构型的时均流场和瞬时流场;最后给出了两种射流构型下中场两个监测点的噪声频谱以及远场噪声指向性。
非定常模拟得到的时均升/阻力系数如表 2所示。射流对升力系数基本没有影响,同时降低了增升装置的阻力,射流的应用维持了增升装置的原有增升性能。
| CL | CD | |
| Baseline | 1.695 | 0.0268 |
| cμ=0.00243 | 1.695 | 0.0241 |
| cμ=0.00547 | 1.691 | 0.0243 |
图 9描绘了基准构型和喷流构型下缝翼凹坑内展向涡wzcstowed/u∞(wz为展向角速度)的时均云图。从时均云图可知,基准构型在空腔的中央存在很明显的涡系,射流打散了相应区域的涡系。射流后在喷缝远离尖端的边缘新生有一剪切层,当加大射流量后,该剪切层的强度有所加大,靠近cusp一端剪切层的强度则有所减小。
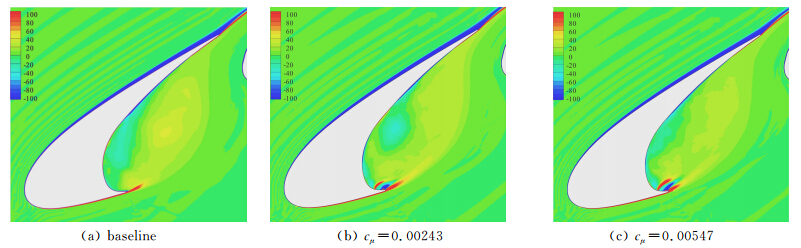 |
| 图 9 时均展向涡云图Fig. 9 Time-averaged spanwise vorticity |
图 10描绘了三种构型下典型的瞬时涡云图。从 图 10可知,射流显著改变了缝翼凹坑内的涡动力学 行为。喷流与新生剪切层的干扰破坏了剪切层展向的拟序结构,减小了展向涡的结构尺寸,削弱了涡的摆动,从尖端脱出去的涡系被很好地限制在一个窄的条带内。这些稳定的小涡对缝翼尾缘的撞击作用较紊乱的大涡要小,由此产生的压力脉动也较小。这些现象与Arunajatesan等[14]所述的空腔射流降噪机理是一致的。同时,基准构型下,自由剪切层撞击缝翼尾缘后,剪切层裹挟的涡系回流现象非常显著,这些大尺度、大能量的涡系的回流使凹坑内部流动更加复杂和紊乱,射流后,回流涡系无论是强度上还是规模上比基准构型都要小得多。三种构型下,cμ=0.00243时涡结构最小,当加大射流量后,涡结构和涡强度均有所加大,这表明需要对射流量进行优化,以获得最优的降噪效果。
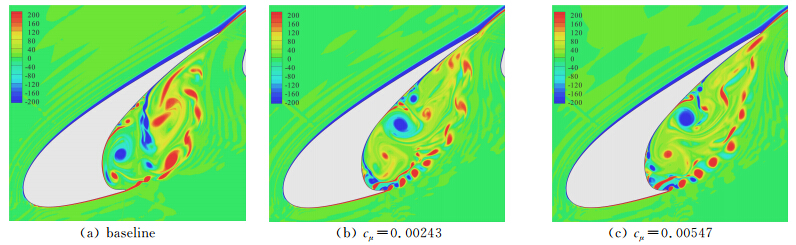 |
| 图 10 瞬时展向涡Fig. 10 Instantaneous spanwise vorticity |
将三种构型的时均流线和时均速度绘于图 11。 从图 11上可知,射流后回流区的宽度变小。有两条分界流线分别源于射流缝道的上下游边缘,这两条流 线往缝翼尾缘发展,并最终通过缝道区域流出。射流 后接近缝翼压力面的回流速度变小,此时回流对新生剪切层的干扰亦会减弱,从而削弱了回流反馈机制。
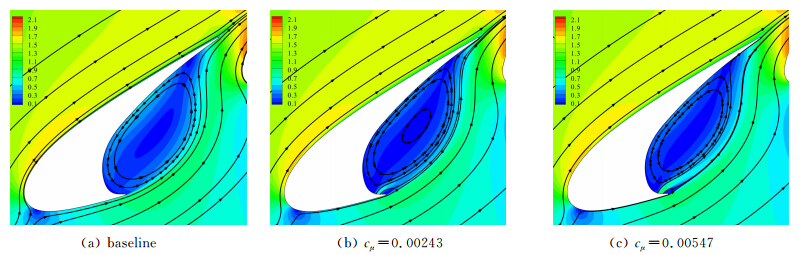 |
| 图 11 时均速度云图和时均流线Fig. 11 Time-averaged velocity magnitude and streamlines |
图 12给出了射流后中场两个监测点的噪声频谱与基准构型的对比。可以看出,cμ=0.00243时,在500Hz到7kHz范围内,射流既降低了中场的宽频噪 声,也降低了中场的窄带噪声,在大于7kHz时,点P1 噪声较基准构型要大,点P2没有降噪效果。由于 射流打碎了从尖端脱出去的大涡,使能量由低频向 高频转移,降低了低频噪声的同时,加大了高频噪声。当进一步加大射流量后,降噪效果减弱,且有效频率范围变小。在500Hz到1600Hz范围内,两种射流量降噪效果差别不大,大于1600Hz后,较小射流量所获得的降噪效果较加大射流量后要好;大于6kHz后,较大射流量下的喷流显著加大了噪声。
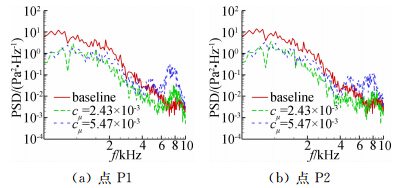 |
| 图 12 射流后中场监测点的噪声能量谱密度Fig. 12 Sound spectra at the near far-field locations with mass injection |
为获得远场噪声特性,将重叠量为50%的六段声源数据分别进行FW-H积分,然后将其得到的远场噪声特性进行平均。远场观测点位于一个以主翼前缘为圆心,角度按逆时针方向增长的半径r=50cstowed的圆上。如图 13所示,远场指向性图接近于偶极子,且指向性垂直于缝翼翼弦。当cμ=0.00243时,在所有角度上均有5~6dB的降噪效果,当加大射流量时,降噪效果随角度的变化而变化。两种射流量下的射流基本没有改变缝翼噪声的远场指向性。
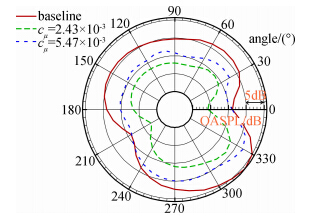 |
| 图 13 远场噪声指向性图Fig. 13 Far-field directivity of OASPL |
本文数值研究了在缝翼尖端附近的压力面上平行射流的缝翼降噪技术。应用DDES计算了二维情况下两段增升翼型FREQUENZ在起降构型下的声源,并用FW-H积分获得了中、远场噪声特性。将基准构型的表面压力系数、空腔速度分布和中场监测点的噪声频谱与实验值进行了对比。对比结果表明本文采用的数值方法准确地模拟了增升装置的气动力学和声学特性,捕捉到了缝翼空腔流动主要的动力学行为。
计算结果表明,前缘射流可以有效地降低缝翼噪声的强度,射流对缝翼和主翼的气动力特性影响不大,升力系数没有变化,阻力系数减小。射流有效地降低了缝翼的宽频和低频窄带噪声,对缝翼远场噪声指向性基本没有影响。
提出了前缘平行喷流降低缝翼噪声的两种机理:
(1) 平行射流与缝翼尖端分离流相互作用,改变了剪切层中的大尺度拟序结构,展向涡的尺度及其不稳定性均得到有效抑制,从而减弱了由于剪切层与缝翼压力面撞击而产生的压力脉动,达到了降低声源强度的目的;
(2) 射流显著地改变了缝翼空腔的流动特性,回流区的宽度变小,靠近缝翼压力面的回流速度变小,削弱了声反馈机制。
同时,由于没有考虑到缝翼流动的三维特性,本研究只能给出一个定性的结论,下一步将开展三维情况下基于前缘平行射流的缝翼降噪技术研究。
| [1] | ARGUELLES P. LUMSDEN J, BISCHOFF M, et al. European aeronautics: a vision of 2020, meeting society’s needs and winning global leadership, report of the group of personalities[C]. The Advisory Council for Aeronautics Research in Europe, 2001. |
| [2] | IMAMURA T, URA H, YOKOKAWA Y, et al. A far field noise and near field unsteadiness of a simplified high lift configuration model (slat)[R]. AIAA Paper 2009 1239. |
| [3] | KOLB A, FAULHABER P, DROBIETZ R, et al. Aeroacoustic wind tunnel measurements on a 2d high lift configuration[R]. AIAA Paper 2007 3447. |
| [4] | DOBRZYNSKI W, NAGAKURA K, GEHLHAR B, et al. Airframe noise studies on wings with deployed high lift devices[R]. AIAA Paper 1998 2337. |
| [5] | CHOW L C, MAU K, REMY H. Landing gears and high lift devices airframe noise research[R]. AIAA Paper 2002-2408. |
| [6] | DOBRZYNSKI W. Almost 40 years of airframe noise research what did we achieve[J]. Journal of Aircraft , 2010, 47(2): 353-367. |
| [7] | KHORRAMI M R, SINGER B A, LOCKARD D P. Time accurate simulations and acoustic analysis of slat free shear layer: part II[R]. AIAA Paper 2002-2579. |
| [8] | MEHDI R K, DAVID P L. Effects of geometric details on slat noise generation and propagation[J]. International Journal of Aeroacoustics , 2010, 9(4&5): 655-678. |
| [9] | IMAMURA T, URA H, YOKOKAWA Y, et al. Designing of slat cove filler as a noise reduction device for leading edge slat[R]. AIAA Paper 2007-3473. |
| [10] | VICTOR F K, MIKHAIL Y, ZAITSEV, et al. Noise reduction potential through slat hook serrations[R]. AIAA Paper 2011 2909. |
| [11] | THILO K, FRANK T. Slat noise reduction using steady suction[R]. AIAA Paper 2008 17. |
| [12] | WELLS A K. Slat aerodynamics and aeroacoustics with flow control[D]. Southampton: University of Southampton, 2007. |
| [13] | CHEN P. Identification and attenuation of slat noise[D]. Southampton: University of Southampton, 2012. |
| [14] | ARUNAJATESAN S, KANNEPALLI C, SINHA N, et al. Suppression of cavity loads using leading edge blowing[J]. AIAA Journal , 2009, 47(5): 1132-1144. |
| [15] | ZHUANG N, ALVI F S, ALKISLAR M B, et al. Supersonic cavityflows and their control[J]. AIAA Journal , 2006, 44(9): 2118 2128. |
| [16] | ALISON M L, CHOKANI N. Computation of cavity flows with suppression using jet blowing[J]. Journal of Aircraft , 1997, 34(4): 545-551. |
| [17] | SARNO R L, FRANKE M E. Suppression of fiow induced pressure oscillations in cavities[J]. Journal of Aircraft , 1994, 31(1): 90 96. |
| [18] | MICHEL U, ESCHRICHT D, GRESCHNER B, et al. Advanced DES methods and their application to aeroacoustics[J]. Notes on Numerical Fluid Mechanics and Multidisciplinary Design , 2010, 111: 59-76. |
| [19] | LOCKARD D P, CHOUDHARI M M. Noise radiation from a leading edge slat[R]. AIAA Paper 2009 3101. |
| [20] | KONIG D, KOH S R, MEINKE M, et al. Two step simulation of slat noise[J]. Computers and Fluids , 2010, 39: 512-524. |