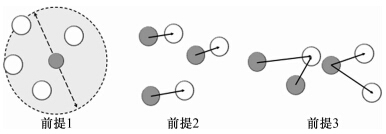
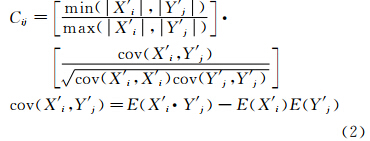近20年来,得益于实验能力的发展,如扩大的数据存储量和提高的采集频率等,粒子图像测速技术得到了长足的发展。基于当代实际应用的需求,对流场的非接触式光学测量的工作重心已经转移至流场的整场瞬时三维测量及单粒子的三维拉格朗日追踪,从而对单粒子运动三维统计特性进行细致的量化分析;而这些对于传统的PIV互相关(或自相关)算法[1, 2]来说是无法完成的任务。发展相关拉格朗日追踪技术的尝试始于准三维(stereo)视角下第三方向速度分量的计算[3, 4, 5, 6]并在随后达到了真正的粒子三维识别[7, 8, 9, 10, 11]。真三维实验中,成像系统在任一瞬时的产物是粒子群的瞬时三维坐标,这同样也是三维粒子追踪算法(3D Particle Tracking Velocimetry,简称3D PTV)的输入量。本文对一种经典PTV实施三维化,从而使之能够匹配来自连续两帧的三维粒子团。此PTV的二维版本是基于三角嵌铺(Delaunay Tessellation)的PTV[12],它具有两大特点:结构的简洁性及处理强旋转流场的能力。首先,对PTV算法的粒子样型(pattern)及计算前提进行介绍。常见的PTV粒子样型包括以下几类:同帧粒子形成的几何构架[13, 14]、这种几何构架的自定义标识[15, 16]以及所有可能存在的匹配的数学化组合[17, 18]。匹配的粒子样型即分别来自连续两帧的、处于一定空间条件限制下的最相似样型,而PTV从样型匹配结果中总结粒子匹配,故粒子样型匹配属于表层匹配。PTV的计算假设及标准最初由Baek和Lee[19]定义。由于本文仅考虑两帧PTV,故结果只涉及一个“速度”,即呈匹配关系的两粒子的空间距离与两帧时间间隔之比。 文献[19]中阐述的PTV计算前提可简化如下(图 1所示;其中来自第一、第二帧以及确定为候选的粒子分别由灰色、白色及黑色表示,粒子匹配关系由箭头表示):
 |
| 图 1 PTV算法前提Fig. 1 Heuristics for PTV algorithm |
前提1: 单粒子两帧间的有限位移,它是确定候选样型及实现表层匹配的基础;
前提2: 一定范围内同帧粒子的相似性运动,即局部拟平行运动;
前提3: 匹配逻辑性,实际上是剔除伪逻辑匹配的要求而非假设性前提。
作为一种典型的粒子群匹配算法,DT PTV的粒子样型是同帧相邻粒子构成的Delaunay三角形(对于三维情况来说是Delaunay四面体)。DT PTV仅遵循前提1的特性可以解释其算法结构的简洁性。首先从二维版本的DT PTV入手说明将其扩展至三维领域的措施。 1 DT PTV及其三维版本 1.1 粒子样型匹配
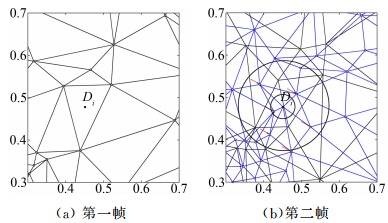
作为DT网格的基本构成元素,DT三角形是二维DT PTV的粒子样型,如图 2所示。在DT网格生成以后,第一步应将两帧的粒子样型进行匹配。假设第一帧中一任意DT三角形Di(Di同时表征其形心,如图 2a所示,其中灰色圆和实线分别表示粒子及DT网格)。通过采用前提1以及Di坐标,所有形心落入既定查询域的第二帧DT三角将被确定为候选粒子样型(如图 2b,其中粗、细线分别表示粒子DT网格和样型DT网格,样型形心由白色正方形表示)。
 |
| 图 2 DT PTV中候选粒子样型的确定Fig. 2 Determination of the pattern candidates in DT PTV |
此措施并非完全用于算法的三维化拓展,而是使DT PTV 消除最后一个常数参量,即上文所述用来圈选候选粒子样型的查询域半径。虽然仍立足于前提1,但候选粒子样型不再由固定的查询域半径而是由一种网格确定:DT粒子样型网格,它由Di及第二帧所有粒子样型形心共同构成,其中,任何与Di直接相连的形心所对应的粒子样型均被确定为候选样型,如图 2b中箭头所示。此措施的有效性在于总能保证将真正的匹配样型确定为候选,而不会因圈选半径太大造成冗余选择或圈选半径太小而遗漏真正的匹配样型(图 2(b))。至此,DT PTV对速度非均匀分布的粒子流场完全适用;更重要的是,DT PTV完全独立于任何固定阈值的预设,从而避免了匹配准确率对固定阈值变化可能的敏感反应。 1.3 三维化扩展的措施之二
当Di的候选样型确定之后,问题转化为其中哪一个样型与Di在几何程度上最为相似。如图 3(a)所示,Song等[12]通过对待匹配样型(三角形)Xi和Yj(X和Y分别表示前后两帧,小写字母同义)进行形心重叠并由二者重叠面积计算样型相似准数Cij,其中S为面积运算:
 |
| 图 3 DT PTV样型相似性的传统计算方法Fig. 3 Traditional way to calculate the pattern similarity |
为达到不受具体流型干扰的无偏差运算,Song等[12]做出了进一步调整:将形心重叠的xi和yj进行旋转,在保证两个样型的三边(或三内角)大小顺序在顺(或逆)时针方向上一致的前提下,将样型中连接形心及某顶点的两条直线重合,最终得到新的样型重叠面积(图 3b)。在三维流场中,DT PTV的粒子样型是四面体,对其来说三维旋转及四面体对的重叠体积运算绝非最简洁的处理方式。因此,本文提出一种针对四面体的“样型唯一性标识向量”来得到一个纯数学性的相似性运算。作为四面体一对一的标识,此标识向量由四面体四个侧面的面积组成,并且其元素进行了升序或降序排列来达到图 3(b)所示的旋转效果。值得注意的是,对于两个比较之中的四面体样型,二者标识向量的元素须同为升序或降序排列。因此,三维版本的样型相似准数如下所示:
其中X ′i和Y ′j表示来自前后两帧的待匹配样型的标识向量,绝对值符号代表对向量取模,E为数学期望运算。Cij由两部分构成(中括号隔开):左边部分考虑标识向量的模(即四面体)的体积,右边部分计算向量互相关性。最大Cij所对应的候选样型即为目标样型的匹配样型。值得注意的是存在这样一种可能性:两个或多个候选样型均具有最大且相同的相似准数;然而DT PTV的核心概念恰恰能够利用这种可能性,这将在1.5节详述。 1.4 归纳粒子匹配从样型匹配结果中归纳出粒子匹配的方法很简单:作为已匹配样型的顶点,两组待匹配离散点的匹配顺序由各自所对应的四面体侧面积(即标识向量的元素)大小顺序所决定。如图 4所示,若已知Xi和Yj匹配,且如下具备侧面积大小顺序:
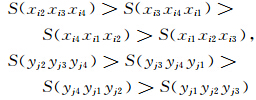
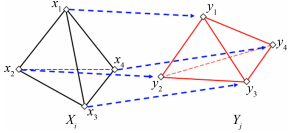 |
| 图 4 由样型匹配至粒子匹配Fig. 4 From the pattern pairing to the particle pairing |
完整的粒子匹配粗结果由全部完成的样型匹配结果汇总得到。由于冗余噪音干扰及DT PTV的核心概念:一个粒子的匹配结果由其所在的所有样型共同决定,那么对于一个粒子而言非常可能的一个结果就是粒子匹配的冗余,具体表现为重复或伪逻辑(矛盾)匹配。利用DT网格进行伪矢量剔除的传统方法是首先将粒子匹配关系表示为具有一定大小及方向的速度矢量,并以连续性假设为基础计算粒子样型中的净流量[12]。图 5给出二维示例。{v1,v2,v3}是所在粒子样型的匹配矢量组合之一,则其净流量Q为:
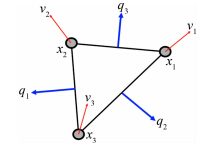 |
| 图 5 传统方法提剔除冗余匹配Fig. 5 Traditional way to remove spurious vectors |
在此重述与颗粒相的连续或离散属性无关的伪矢量剔除方法:双向计算-概率择优[22]。双向计算是指以“第一帧指向第二帧”以及相反的方向进行两次PTV运算,并将后一个粒子匹配结果转化为“第二帧指向第一帧”的模式并将两部分结果合并。双向计算可行的原因在于DT PTV简洁的算法结构所致的快速运算允许此种重复。接下来,概率择优选取重复出现次数最多的匹配并删除一切矛盾匹配,并将被删清匹配的粒子标记为“无匹配”。图 6为一个算例,其中x和y分别表征来自前后帧的粒子,数字代表粒子在其所在帧的序号。双向算法以一种合理的方式扩大了粒子匹配的样本空间:匹配样本空间越大,越符合DT PTV的核心概念。或者说,双向计算强化了概率择优的有效性,这也是双向计算再度被强调应用于DT PTV的原因。此方法立足于算法结构而不是颗粒相物理属性,并保证伪逻辑匹配的完全清除。
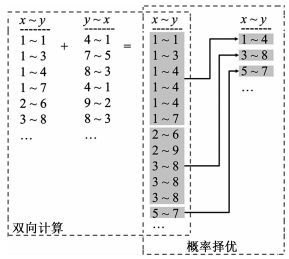 |
| 图 6 双向计算实例Fig. 6 Example of the dual computation |
DT PTV通过上述措施被正式扩展至三维领域并命名为3DT PTV。其算法结构如图 7所示,其中灰色和白色分别代表算法模块和阶段产物。值得注意的是上述措施及其思想均可用于DT PTV的二维版本。更为重要的是,第一个(DT网格代替固定阈值确定候选匹配样型或粒子)及第三个措施(双向计算-概率择优)适用于所有PTV算法。然而第二个措施:DT PTV 粒子样型的相似性判断是一种针对三维DT PTV的算法简化而非准确率的提高手段,故在检测环节中它将直接被用于所有亚类型的DT PTV算法。
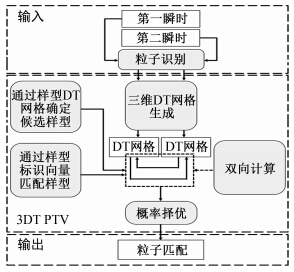 |
| 图 7 3DT PTV算法结构Fig. 7 Structure of 3DT PTV |
NRX[23](New Relaxation Based PTV)是更新版的基于迭代的粒子追踪算法[19],其原型是一种应用于人群及交通工具的运动图像识别算法[24],将其选为检验DT PTV的比较算法具备多重原因。首先,它在当前作为一些3D3C(三维,三相机)流场分析系统的粒子匹配算法,如V3V[11];其次,它是能够对大梯度复杂流场及“粒子无匹配”进行良好处理的一类PTV算法的优秀代表;最后,它也是遵循算法前提2的一类PTV的典型代表,即目标粒子的所有可能匹配均以其空间临近匹配为参照进行检测取舍。在NRX中所有粒子的可能匹配及粒子无匹配均由数字概率值表达:前后两帧的粒子分别由x和y表示,假设Pij是xi与yj匹配的概率,而Pi是xi无匹配的概率;Pij和Pi通过各自包含若干自定义参数的迭代式进化,大约经过20次迭代可达到收敛;最终,对应最大Pij的yj将被选为xi的匹配粒子;如果Pi是最大概率,xi则被标识为无匹配。 2.2 两种PTV的比较
对于PTV算法来说,对不同算法前提的遵循将对自身匹配样型结构及参数依赖性产生直接影响。3DT PTV和NRX均遵循算法前提1;与NRX相反的是,3DT PTV的运行与算法前提2无关;此外,为了满足算法前提3即无伪逻辑匹配,NRX需要额外的方法来消除伪矢量(大多数呈“多对一”形式)。然而,鉴于2.5节所述的双向算法的普适性,它将被应用于两种PTV算法来达到公平比较。 3 算法检测 3.1 人工流场
两种算法通过Okamoto等[25]发展的被广泛认可和应用[23, 26, 27]的JPIV标准人工流场来进行检测和比较,这也是双向算法相对文献[22]来说第一次在与不同类型的PTV算法比较下接受标准流场检验。使用者可通过直接比较自身PTV计算结果与人工真实结果来得到算法准确率。共采用其中八个三维工况,其中每个工况包含了一定数量、用来描述流场连续运动的连续瞬时序列;除了以序号表征的所有连续两帧的真实匹配结果,序列中的每一个瞬时的原始数据包括一对模拟stereo PIV拍摄的图像对以及对应的真实粒子三维坐标。通常来讲粒子的三维坐标应通过对上述准三维图像对进行匹配得到;然而本文直接利用两帧真实粒子三维坐标作为三维PTV算法的唯一输入数据,这是因为准三维构架并非本文的工作内容或目标,而且如上文所述,仅以坐标矩阵为唯一输入数据的形式与3D PTV在实际系统中的应用一致[11]。
本文应用的人工流场为不同参数下存在壁面反射的CFD三维射流,是剪切、旋转及空间非均匀分布性的良好组合;条件参数包括固定“照明”区域下的“照明”架构、粒子数量(浓度)以及对应的粒子进入和逃逸率,如表 1和2所示,表 1中两帧间粒子差若为负数则表示前帧粒子数小于后帧;表 2中进入(逃逸)粒子比率即进入(逃逸)粒子数量与两帧中前一帧粒子数量之比。某一瞬时的空间非均匀分布性由三维粒子DT网格的所有四面体单元的最小及最大边长的比值来表征,而一个工况的非均匀度θ则是1与其所有瞬时空间非均匀分布性的平均值之差,因此对一个理想化的完全均匀分布的流场来说θ= 0。
| serial-name | description | instant number | particle number | inter-frame difference | ||
| min. | max. | min. | max. | |||
| 1-301C | 3D slit light sheet | 145 | 3737 | 4202 | -40 | 54 |
| 2-302C | 3D slit light sheet | 145 | 864 | 1010 | -27 | 26 |
| 3-331 | Stereo PIV | 145 | 2151 | 3601 | -56 | 54 |
| 4-337 | Stereo PIV | 201 | 6501 | 6883 | -44 | 51 |
| 5-351 | 3D 3 angles with wall refraction | 145 | 1150 | 2138 | -31 | 21 |
| 6-352 | 3D 3 angles with wall refraction | 145 | 306 | 377 | -10 | 12 |
| 7-371 | 3D 3 angles with wall refraction | 145 | 321 | 431 | -15 | 15 |
| 8-377 | 3D 3 angles with wall refraction | 201 | 811 | 171 | -14 | 13 |
| serial-name | minimum dmfm-1 | entering | escaping | ||||||
| number | ratio/% | number | ratio/% | ||||||
| min. | max. | min. | max. | min. | max. | min. | max. | ||
| 1-301C | 2.24 | 110 | 227 | 2.70 | 5.61 | 113 | 231 | 2.72 | 5.82 |
| 2-302C | 1.25 | 11 | 63 | 2.04 | 6.25 | 21 | 71 | 2.16 | 7.42 |
| 3-331 | 2.51 | 123 | 318 | 3.36 | 8.85 | 111 | 211 | 3.28 | 8.30 |
| 4-337 | 1.36 | 101 | 216 | 1.58 | 3.13 | 103 | 240 | 1.41 | 3.31 |
| 5-351 | 4.41 | 33 | 74 | 1.55 | 3.41 | 34 | 76 | 1.57 | 3.65 |
| 6-352 | 24.52 | 2 | 18 | 0.54 | 5.56 | 2 | 17 | 0.60 | 4.86 |
| 7-371 | 11.60 | 4 | 28 | 1.08 | 7.84 | 3 | 26 | 0.77 | 6.81 |
| 8-377 | 1.57 | 2 | 26 | 0.21 | 2.64 | 1 | 20 | 0.11 | 2.08 |
在通过准三维图像重构粒子三维空间分布的过程中,图像极可能存在噪音误差,其直接结果就是一部分真实粒子三维坐标的损失。为了进行更加全面和严格的测试并模拟此种噪音效应,一种自定义干扰被应用于原始真实粒子三维坐标之中。每当两个连续瞬时被确定为PTV的当前处理对象后,通过随机抹除后一帧中一定比例的粒子可实现此干扰添加;换句话说,此干扰并非同时施加于一个瞬时序列中的所有瞬时。此项举措连同固定区域下的粒子进入及逃逸行为共同组成了匹配计算的干扰项,但其相比遵循物理规律的粒子逃逸来讲具备更强的随机性。对每两帧连续瞬时来讲,噪音率是后一帧中所抹除粒子数与粒子总数之比。每个工况中,噪音率以0.5%大小的增幅从0.5%匀速递进至5%,而每个噪音率值对应的准确率是此噪音率值下所有两帧瞬时对的PTV匹配准确率的平均值。 3.3 待检测算法设置
本文着重检测1.2及1.5节所述的两个方法(DT网格确定候选以及双向算法剔除伪矢量)对DT PTV及NRX的作用,因此在每个工况中,基于候选样型(粒子)的确定及剔除伪逻辑匹配两方面的不同,共有源于DT PTV 和NRX的八种PTV算法进入检测,如表 3所示,其中第四个PTV算法即3DT PTV。综上,准确率是由噪音率和PTV具体类型共同决定的函数。 表 3中NRX 1~4的计算参数根据Ohmi和Li[22]的分析进行最优化赋值,如3.1节所述。原始数据中,两帧间粒子最大位移dm被用来确定NRX的参选粒子(来自目标粒子的同一帧)及候选(来自另一帧)的圈选半径:对于表 3中的DT PTV 1、2 及NRX 1、2来说候选圈选半径Rc略大于dm;NRX 1、2的参选圈选半径Rr=2.5Rc;对于NRX 3、4来说DT网格的概念被用于单粒子xi的候选粒子的选取:包括xi在内的所有第一帧粒子所组成的DT网格中,任何与xi直接相连的粒子将被选作参选粒子。DT PTV 1~4均采用1.3节的措施进行粒子样型相似性判断,但如上文所述,此措施只是一种算法简化而并非准确率的改进。
| type/name | candidate or reference selection | removal of spurious pairings |
| DT PTV 1 | fixed radius | minimum net flux,Song et al.[12] |
| DT PTV 2 | fixed radius | dualcomputation |
| DT PTV 3 | method in Section 1.2 | minimum net flux,Song et al.[12] |
| DT PTV 4 (3DT PTV) | method in Section 1.2 | dualcomputation |
| NRX 1 | fixed radius | minimum net flux,Song et al.[12] |
| NRX 2 | fixed radius | dualcomputation |
| NRX 3 | method in Section 1.2 for both candidate and reference selection | minimum net flux,Song et al.[12] |
| NRX 4 | method in Section 1.2 for both candidate and reference selection | dualcomputation |
图 9显示了八种工况下四种DT PTV算法随噪音率升高的准确率的变化,所有工况结果定性一致。采用了“双向计算-概率择优”的DT PTV在剔除伪逻辑匹配上明显优于遵循粒子样型“最小净流量”原则的DT PTV,因此四种DT PTV因准确率差异被划分为两组,每组中两个DT PTV的差异在于候选粒子样型的确定方法。见图 9,一方面,这种DT网格相对于固定阈值选择有明显的优越性:对于PTV来说,因不当的阈值半径而产生的冗余候选粒子样型与目标样型几何相似空间距离相差较远,仅通过样型相似性分析无法进行筛分,所以PTV算法对更好的样型候选确定方式有更敏感的正反应; 另一方面,当噪音率线性增长时,所有DT PTV算法均明显降低,其中经典算法 (DT PTV 1)尤甚。这是因为对于DT PTV来讲,粒子缺失比粒子冗余产生的干扰更加强烈,局部个别冗余粒子样型很难影响到他们所共同包含的某个粒子的匹配,因为这些粒子同时被其他真是粒子样型所包含;而源于粒子缺失的样型缺失则会削减双向算法中概率择优模块所对应的样本空间,并同样造成经典DT PTV的计算错误,因为对经典版本来讲,样型匹配层面的结果永远不可能是“无匹配”。总而言之,3DT PTV 相比经典版本发挥更优。
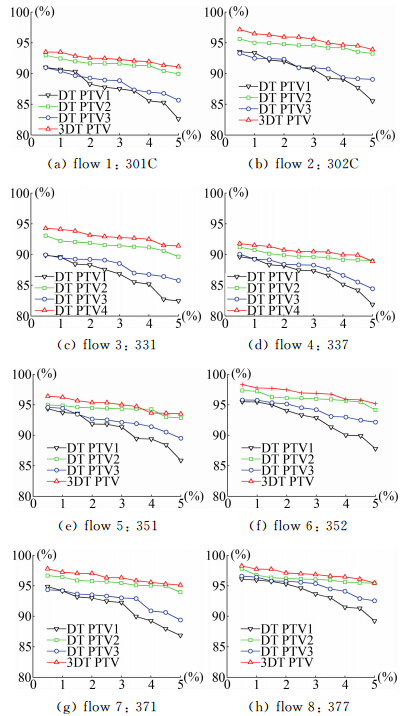 |
| 图 8 DT PTV的匹配准确率Fig. 8 Accuracy of 3DT PTV |
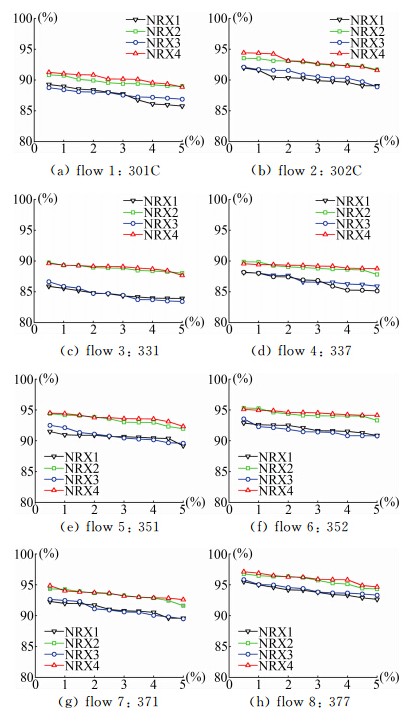 |
| 图 9 NRX的匹配准确率Fig. 9 Accuracy of NRX |
NRX的检验结果与DT PTV总体上定性一致:“双向计算-概率择优”的优越性同样将四种NRX按照准确率优劣划分为两组,如图 10所示。但每组中的两种NRX算法表现相近,说明对于NRX来说,在粒子空间非均匀分布度适中的情况下,DT网格在确定候选及参选粒子上并不比固定阈值法更加优越。特别地,DT网格所确定的参选粒子数量极有可能比固定阈值所确定的小,那么NRX中匹配概率的迭代活性则会相应地减弱。
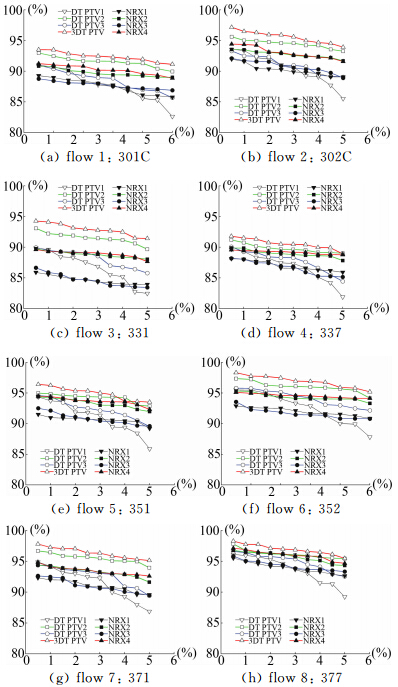 |
| 图 10 两种算法间的比较Fig. 10 Comparison between DT PTV and NRX |
上述DT PTV及NRX的结果于图 11中一并显示(图例同图 8、图 9),可看到3DT PTV在所有八种算法中表现最优,其次是通过固定阈值确定候选的双向DT PTV,然后是两种双向NRX算法;DT网格确定候选及双向算法剔除伪矢量的普遍有效性得到验证。另外,随着噪音率线性增长,从准确率的衰减率(即准确率曲线的斜率)来看,NRX小于DT PTV;这是因为NRX更善于处理“粒子无匹配”问题,而粒子进入或冗余行为则是其真正的挑战。这恰好说明了文中所述措施对于DT PTV的意义更大,因为在三维重建中真实粒子坐标缺失的可能性远大于粒子坐标冗余。 5 结 论
仅仅基于“单粒子两帧间位移有限”的假设,DT PTV被扩展至三维领域并保持了结构的简洁性和参数无依赖性。加入自定义干扰的标准人工流场证实了所述改进措施的有效性及DT PTV的良好适应性;在同样的环境下3DT PTV与NRX表现相当或更好,但却在算法初始参数设置的简洁性上更胜一筹。尽管缺乏实验算例,但文中过程仍是检验PTV 的有效手段,因为人工流场的普遍应用性、干扰添加的自主性以及PTV输入数据格式与实际三维粒子流场分析工作的一致性。然而必须承认的是,PTV的表现严重受制于第一步工作:粒子空间坐标识别。因此3DT PTV并非是完全独立的理想算法,而更应被看作未来三维粒子识别系统的组成部分及粒子坐标信息的处理模块。
| [1] | WILLERT C, GHARIB M. Digital particle image velocimetry. Exp. Fluids, 1991, 10: 181-93. |
| [2] | WESTERWEEL J, DABIRI D, GHARIB M. The effect of a discrete window offset on the accuracy of cross-correlation analysis of digital PIV recordings. Exp. Fluids, 1997, 23: 20-28. |
| [3] | ARROYO M P, GREATED C A. Stereoscopic particle image velocimetry. Meas. Sci. Technol., 1991, 2: 1181-1186. |
| [4] | SOLOFF S M, ADRIAN R J, LIU Z C. Distortion compensation for generalized stereoscopic particle image velocimetry. Meas. Sci. Technol., 1997, 8: 1441-1454. |
| [5] | KAHLER C J, KOMPENHANS C. Fundamentals of multiple plane stereo particle image velocimetry. Exp. Fluids, 2000, 29: 70-77. |
| [6] | WILLERT C, HASSA C, STOCKHAUSEN G, et al. Combined PIV and DGV applied to a pressurized gas turbine combustion facility. Meas. Sci. Technol., 2006, 17: 1670-1679. |
| [7] | MENG H, PAN G, PU Y, et al. Holographic particle image velocimetry: from film to digital recording. Meas. Sci. Technol., 2004, 15: 673-685. |
| [8] | VIRANT M, DRACOS T. 3D PTV and its application on Lagrangian motion. Meas. Sci. Technol., 1997, 8: 1539-1552. |
| [9] | ELSINGA G E, SCARANO F, WIENEKE B, et al. Tomographic particle image velocimetry. Exp. Fluids, 2006, 41: 933-947. |
| [10] | SCHRODER A, GEISLER R, ELSINGA G, et al. Investigation of a turbulent spot and a tripped turbulent boundary layer flow using time-resolved tomographic PIV. Exp. Fluids, 2008, 1: 305-316. |
| [11] | HILL D, TROOLIN D, WALTERS G, et al. Volumetric 3-component velocimetry (V3V) measurements of the turbulent flow in stirred tank reactors. 14th Int. Symp. Applications of Laser Techniques to Fluid Mechanics. Lisbon, Portugal, 2008. |
| [12] | SONG X, YAMAMOTO F, IGUCHI M, et al. A new tracking algorithm of PIV and removal of spurious vectors using Delaunay tessellation. Exp. Fluids, 1999, 26: 371-380. |
| [13] | UEMURA T, YAMAMOTO F, OHMI K. High speed algorithm of image analysis for real time measurement of two-dimensional velocity distribution. KHALIGHI B, et al, Eds. Flow Visualization. ASME FED, 1989: 129-134. |
| [14] | YAMAMOTO F, UEMURA T, TIAN H, et al. Three-dimensional PTV based on binary cross-correlation method. JSME Int. J., 1993, 36: 279-284. |
| [15] | OKAMOTO K, SCHMIDL W D, HASSAN Y A. Least force technique for the particle tracking algorithm. CROWDER J P. Ed. Flow Visualization VII. New York: Begell House, 1995: 647-652. |
| [16] | ISHIKAWA M, MURAI Y, WADA A, et al. A novel algorithm for particle tracking velocimetry using the velocity gradient tensor. Exp. Fluids, 2000, 29: 519-531. |
| [17] | KIMURA I, HATTORI A, UEDA M. Particle pairing using genetic algorithms for PIV. J. Visualization, 2000, 2: 223-228. |
| [18] | LABONT′E G. A new neural network for particle-tracking velocimetry. Exp. Fluids, 1999, 26: 340-346. |
| [19] | BAEK S J, LEE S J. A new two-frame particle tracking algorithm using match probability. Exp. Fluids, 1996, 22: 23-32. |
| [20] | WANG D W, WANG Y, YANG B, et al. Statistical analysis of sand grain/bed collision process recorded by high-speed digital camera. Sedimentology, 2008, 55: 461-470. |
| [21] | WANG Y, WANG D W, WANG L, et al. Measurement of sand creep on a flat sand bed using a high-speed digital camera. Sedimentology, 2009, 56: 1705-1712. |
| [22] | ZHANG Y, WANG Y, WANG D W. Elimination of discrete phiase outliers in DT-PTV by preferential probability. Journal of Xi'an Jiaotong University, 2009, 43: 119-123.(in Chinese) 张洋, 王元, 王大伟. DT-PTV离散相伪矢量的概率择优式剔除算法. 西安交通大学学报, 2009, 43: 119-123. |
| [23] | OHMI K, LI H Y. Particle-tracking velocimetry with new algorithms. Meas. Sci. Technol., 2000, 11: 603-616. |
| [24] | BARNARD S T, THOMPSON W B. Disparity analysis of images. IEEE Trans Pattern Analysis Machine Intelligence, 1980, 2: 333-340. |
| [25] | OKAMOTO K, NISHIO S, KOBAYASHI T, et al. Evaluation of the 3D-PIV standard images. J. Visualization, 2000, 3: 115-123. |
| [26] | BREVIS W, NINO Y, JIRKA G H. Integrating cross-correlation and relaxation algorithms for particle tracking velocimetry. Exp. Fluids, 2011, 50: 135-147. |
| [27] | OHMI K, PANDAY S P, SAPKOTA A. Particle tracking velocimetry with an ant colony optimization algorithm. Exp. Fluids, 2010, 48: 589-594. |