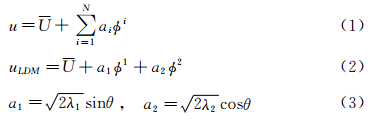2. 中南大学 高速铁路建造技术国家工程实验室,湖南 长沙 410075;
3. 清华大学 航空航天学院,北京 100871
2. National Engineering Laboratory for HighSpeed Railway Construction, Central South University, Changsha 410075;
3. Department of Aeronautics and Astronautics, College of Engineering, Tsinghua University, Beijing 100871, China
一端固定于壁面,另一端为自由端的有限长柱体结构在工程中广泛存在,如超高层建筑、冷却塔、悬索桥或斜拉桥桥塔等等。由于自由端后下扫流的影响,有限长柱体的尾流和气动力特性都与二维柱体的对应情况有显著区别[1]。在下扫流的作用下,有限长柱体的尾流中会出现一对对称的尾流涡[2, 3],使得有限长柱体尾流呈现出显著的三维性。下扫流具有将柱体两侧脱落的展向涡向外侧分开的趋势,这使得有限长柱体尾流中的卡门涡街比二维柱体尾流更宽,而涡脱离频率即St数较小[3, 4]。
壁面边界层条件对有限长柱体尾流也有显著的影响,当边界层厚度相对较小时,其影响可忽略,尾流中的三维性主要由下扫流所控制;而当边界层厚度较大时,柱体尾流中会出现一个与下扫流相反的“上升流”[3, 5]。伴随该上升流,在尾流底部会出现一对与尾流涡旋向相反的底部涡[5]。随着尾流向下游的发展,底部涡的衰减速率快于顶部涡[3, 5]。
众多的试验结果显示,有限长柱体的高宽比或长径比(H/d,其中H为柱体高度,d为柱体特征宽度)对柱体所受气动力和尾流结构有很大的影响[1, 3, 6]。部分学者[6, 7]认为,当H/d大于某一临界值时,柱体尾流中除靠近自由端附近的区域外,大部分区域仍被交替脱落的展向涡所控制,类似于二维柱体尾流中的Karman涡街;而当H/d小于该临界值时,交替脱离的展向涡会消失,整个尾流被下扫流所控制,并呈现出对称状态。对于圆形柱体,这一临界值为3~4左右;而对于方形截面柱体,该临界值则略小[6, 7]。通过系统的研究H/d=3~11的方形柱体尾流,Wang和Zhou[1]发现对该高宽比范围内的柱体,自由端上剪切流都会将柱体两侧剪切流连接在一起,构成一个封闭的整体涡结构。尾流涡和可能出现的底部涡都是该涡结构在流向平面内的投影。最近,日本学者Kawai等[8]通过高频3D-PIV试验验证了这一结论的正确性。此外,当H/d=5和7时,柱体尾流中都可以观察到Karman涡街和对称涡结构两种典型流动状态[1, 5]。显然,当尾流中出现上述两种不同的流动状态时,柱体所受的气动力特性将有显著的差异。当Karman涡街出现时,柱体的阻力系数(CD)较大,相应的脉动升力系数(C′L)也较大;而当尾流结构呈对称形态时,CD和C′L均较小[1]。通过测量H/d=5的柱体侧面中间高度上的压力系数(Cp)随时间的变化规律,Sattari[9]观察到了类似的现象,即Cp随时间的变化规律有两种典型的状态。某些时候,Cp会出现周期性显著的大幅波动;而另一些时候,Cp的波动幅度很小且没有明显的周期。
上述结果均是通过观察有限长柱体尾流或表面压力的瞬态测量结果而得到的,尾流中上述两种典型状态的内在关系以及他们与二维柱体尾流的区别仍不清楚。针对这些问题,本文对H/d=7的正方形棱柱中间高度展向平面内流场进行了PIV测量及POD分析。为方便对比,在相同实验条件下对二维方柱尾流也进行了测量。POD分析为进一步了解有限长柱体尾流特性,特别是上述两种典型状态的关系提供了新的角度。 1 实验装置
实验是在一闭式循环风洞中进行的,实验段宽0.6m,高0.6m,长2.4m,实验模型如图 1所示。有限长正方形棱柱一端固定在平板上,柱体宽度d=20mm,高宽比H/d=7。平板距离风洞底面约0.15m,以避免风洞壁面边界层的影响。为防止流动分离,平板前缘加工成光滑弧形。柱体中心距离平板前缘0.3m。实验中,自由来流速度(U∞)为7m/s,对应的Red=9300。实验装置所带来的风洞阻塞度约为3%,阻塞效应可忽略不计。柱体所在位置上的平板边界层厚度为27mm,即1.35d。坐标系的定义如图 1所示,其中x为流动方向,y为宽度方向,z为高度方向。
 |
| 图 1 实验装置与PIV测量平面示意图 Fig. 1 Schematic diagram of the experimental setup and the PIV measurement plane |
一热线探针固定在有限长棱柱尾流中x*=3,y*≈1.5,z*=3.5的位置上,以检测尾流中的涡脱落频率。本文中上标“*”表示以U∞或d进行无量纲化。探针连接在恒温热线风速仪上,过热系数为 1.6。热线信号经1.5kHz低通虑波后,以3kHz的频率进行采样,采样时间为20s。对热线信号进行FFT变换后,可依据能谱峰值对应的频率确定尾流中的涡脱落频率。本文中以上述方法所确定的涡脱落频率的误差为±0.86Hz,对应St数的相对误差为±2.3%。
本实验所使用的PIV激光器最大脉冲能量为120mJ,CCD分辨率为1280×1024pixel2,系统的测量频率为3.75Hz。实验中采用石蜡油产生的烟雾作为示踪粒子,油滴粒径在1~5μm范围内,具有良好的跟随性。运用该PIV对z*=3.5的展向平面内流动进行了测量,如图 1所示。测量中,图像的空间分辨率为153μm/pixel,对应实际测量范围约为196×156mm2。互相关算法所用查问区间为32×32pixel2,两个方向上重叠率均为50%。在相同Red的条件下对二维方柱尾流也进行了类似的PIV测量,以提供对比参照。通常认为PIV测量得到的瞬态速度包含有系统误差和随机误差。经认真标定,系统误差可忽略不计;而随机误差的影响因素众多,如颗粒浓度、颗粒尺寸、空间分辨率等[10]。对于本实验所研究的湍流钝体尾流场,瞬时场采样数为1500帧,以确保统计量和POD分析的可靠性。以上述的1500个瞬态样本计算时均速度、雷诺应力和速度rms值的统计误差分别为2%、9%和6%左右[11]。 2 实验结果 2.1 时均结果
图 2所示为二维方柱尾流中x*=2处时均流向速度U* 、雷诺应力u*v* ,以及流向与侧向脉动速度的rms值u*rms和v*rms的分布情况。文中“-”表示时间平均量。图 2中同时给出了二维方柱尾流中的LDV测量结果[12]作为对比。可看出,本文PIV结果与文献中的LDV测试结果吻合的较好,这验证了本次实验结果的可靠性。
 |
| 图 2 二维方柱尾流中的时间平均结果,x*=2 Fig. 2 Time averaged results in 2D square cylinder wake,x*=2 |
图 3给出的是二维棱柱和有限长棱柱尾流中U方向脉动速度的能谱。在二维方柱尾流中,能谱峰值出现在f*s=0.13处,这与文献[12, 13]所报道的结果是一致的。而对于H/d=7的柱体,St数为0.11,略小于二维棱柱的对应值。这是因为有限长柱体尾流中的下扫流具有将柱体两侧脱落的展向涡向外侧分开的趋势,从而延长了展向涡的脱落时间,所以降低了有限长柱体尾流中的涡脱离频率[4]。此外,如图 3所示,有限长棱柱尾流中能谱的尖峰要明显弱于二维棱柱,且尖峰的宽度也相对较大。这说明,尽管H/d=7的柱体尾流中有周期性的涡脱落现象,但其涡强度要弱于二维钝体尾流,这一特性将在下面尾流的POD分析中进一步讨论。
 |
| 图 3 流向脉动速度能谱 Fig. 3 Power spectral density function of U |
本征正交分解(POD)法是基于主元分析(PCA)思想,依据Karhumen-Loève展开,将流场进行分解,并按照能量比计算出各阶模态,识别出流动中大尺度的拟序结构[14]。本文中用于PIV数据分析的POD方法是由Sirovich提出的快照POD(Snapshot POD)算法[15]。首先,将瞬时流场分解为时均速度场和脉动速度场,即u(x)=u(x)+u′(x),然后对脉动速度场进行POD分解。最终,全部流场信息可分解为时均流场(0阶模态)和脉动流场(已分解为1,2,3…阶模态)。任意瞬时流场可视为各阶模态的线性组合。POD方法已经成功的用于多种湍流速度场、涡量场以及压力场的研究中[14, 16, 17, 18, 19]。
图 4给出了二维方柱尾流场的1-3阶模态对应的以无量纲涡量为背景的速度矢量图。这一结果与van Oudheusden等[20]所报道的二维方柱尾流中的结果是一致的。在1、2阶模态中可清晰的看到正负交替的Karman涡街。1、2阶模态是完全相似的,仅相位上相差1/4个涡脱离周期。3阶模态所对应的正负涡量呈现出关于中心线对称的形态,这与1、2阶模态是截然不同的。此外,3阶模态的涡强度也显著小于1、2阶模态对应值,这说明在二维方柱尾流中3阶及以上模态对湍流脉动带来的贡献是非常有限的,这一点将在各阶模态对应的能量分布中进一步讨论。
 |
| 图 4 二维方柱尾流中的1-3阶模态对应的流动结构 Fig. 4 Flow structures of 1-3 POD modes in 2D square cylinder wake |
图 5给出了H/d=7的棱柱尾流中间高度(z*=3.5)截面内1-3阶模态的矢量与涡量图。与二维方柱对应结果(如图 4所示)有很多定性的相似之处:首先,1、2阶模态的涡量呈现出类似Karman涡街的正负交替的形态,且两者空间上也是相差1/4周期;其次,1,2阶模态对应的涡量强度明显大于3阶模态的对应值;此外,3阶模态所对应的涡量与速度矢量图也呈现出关于中心线对称的结构。除上述定性上的相似点外,图 4与图 5存在着显著的差异。H/d=7棱柱尾流中1、2阶模态的涡量值要明显小于二维柱体尾流中的对应结果,这说明在有限长棱柱尾流中正负交替的涡街结构相对较弱。相对于二维柱体尾流结果,图 5中1、2阶模态的涡结构在y方向明显更宽,表明有限长棱柱尾流要宽于对应的二维柱体尾流,这与文献[1]的结果是吻合的。造成这一现象的原因是有限长柱体自由端产生的下扫流,具有将柱体侧面剪切流向外侧排开的趋势[1, 4]。
 |
| 图 5 H/d=7柱体尾流z*=3.5截面内 1-3阶模态对应的流动结构 Fig. 5 Flow structures of 1-3 POD modes at z*=3.5 in the finite-length prism with H/d=7 |
图 6给出了各阶模态对湍动能的贡献率(不含0阶模态)。对于二维方柱尾流,总湍动能的73.6%(37.2%+36.4%)来自于1、2阶模态,说明Karman涡街在二维方柱尾流中占据了支配地位。而3阶模态所对应的能量约占3.8%,仅相当于1、2阶模态对应能量的1/10左右。在H/d=7的有限长棱柱尾流中,各阶模态的能量分布与二维方柱尾流对应结果有着显著的区别。总体而言,相对于二维方柱,有限长棱柱尾流的脉动能量在较高阶模态中的比重明显增强。代表准Karman涡街的1、2阶模态(如图 5所示)所对应的能量分别为26.7%和19.2%,远小于二维柱体尾流的对应值。而代表着对称尾流结构的3阶模态所对应的能量却达到了9.8%。这说明,在有限长棱柱尾流中类似Karman涡街结构的1、2阶模态对总脉动能量的贡献要显著小于二维柱体尾流,而来自于对称形态的3阶模态和更高阶模态的脉动能量则更多。由此可知,即使H/d=7棱柱的高宽比远大于已有文献所报道的临界值2~3[6, 7],它的尾流结构与二维棱柱尾流也有着显著的差别。
 |
| 图 6 POD各模态能量分布 Fig. 6 Energy distribution of POD modes |
POD方法不仅能识别出流场中各阶模态及其对总脉动能量的贡献,而且可用各模态的线性组合对瞬态流场进行重建,如式(1)所示。其中,U为重建的某一时刻瞬态速度场,U为时均速度场,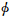 i和ai为第i阶模态所对应的速度场和该模态的系数[15, 21]。对于二维柱体尾流,其1、2阶模态对湍动能的贡献占据了主导地位,如图 6所示。因此,可近似的只用0阶模态(时均场)和1、2阶模态对瞬态流 场进行重建,即“低阶模型法”(Low Dimensional Model,LDM)[22, 23],如式(2,3)所示。
i和ai为第i阶模态所对应的速度场和该模态的系数[15, 21]。对于二维柱体尾流,其1、2阶模态对湍动能的贡献占据了主导地位,如图 6所示。因此,可近似的只用0阶模态(时均场)和1、2阶模态对瞬态流 场进行重建,即“低阶模型法”(Low Dimensional Model,LDM)[22, 23],如式(2,3)所示。
 和
和 分别对其归一化,各瞬态流场对应的点(a*1,a*2)将构成一个圆形[20, 22]。图 7分别给出了二维方柱和有限长棱柱尾流中点(a*1,a*2)的分布。显然,即使是二维方柱尾流,(a*1,a*2)各点也并非严格的落在标准圆形上,而是分散于其两侧。这是由于在Re=9300时,尽管大尺度的Karman涡街在尾流中占了支配地位,但仍有各种小尺度涡甚至随机脉动会对尾流结构带来影响[20]。
分别对其归一化,各瞬态流场对应的点(a*1,a*2)将构成一个圆形[20, 22]。图 7分别给出了二维方柱和有限长棱柱尾流中点(a*1,a*2)的分布。显然,即使是二维方柱尾流,(a*1,a*2)各点也并非严格的落在标准圆形上,而是分散于其两侧。这是由于在Re=9300时,尽管大尺度的Karman涡街在尾流中占了支配地位,但仍有各种小尺度涡甚至随机脉动会对尾流结构带来影响[20]。
 |
| 图 7 各瞬态流场中1、2阶模态对应系数 Fig. 7 Coefficients of the first two modes in the LDM for each instantaneous flow field |
由POD模态重建瞬态流场的方法(如式1所示)可知,a1、a2代表着在瞬态流场重建中1、2阶模态的贡献。因此,图 7中各点距原点的距离R(=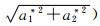 )的大小与1、2阶模态的贡献是成正比的。也就是说,当点P(a*1,a*2)距离原点较远时,1、2阶模态的贡献相对较大;而当点P距离原点较近时,1、2阶模态的贡献则较小。对于二维方柱尾流,没有瞬态点P分布于原点附近(如图 7a所示)。这意味着在二维方柱尾流中1、2阶模态所对应的Karman涡街结构始终占据主导着地位。而在H/d=7的棱柱尾流中,各瞬态点P几乎均匀的分布于平面内,与二维柱体尾流所对应的环形分布有显著的区别。远离原点的点P,其对应的瞬态尾流是由代表着类似Karman涡街的1、2阶模态所支配,这与二维柱体尾流是类似的;而原点附近的点P,其对应的瞬态尾流场中1、2阶模态的贡献可以忽略,此时的瞬态尾流场是由呈对称形态的3阶模态(如图 5所示)或更高阶模态所控制。图 8给出了上述两种典型的尾流状态,其对应P点的位置已在图 7(b)中标出。
)的大小与1、2阶模态的贡献是成正比的。也就是说,当点P(a*1,a*2)距离原点较远时,1、2阶模态的贡献相对较大;而当点P距离原点较近时,1、2阶模态的贡献则较小。对于二维方柱尾流,没有瞬态点P分布于原点附近(如图 7a所示)。这意味着在二维方柱尾流中1、2阶模态所对应的Karman涡街结构始终占据主导着地位。而在H/d=7的棱柱尾流中,各瞬态点P几乎均匀的分布于平面内,与二维柱体尾流所对应的环形分布有显著的区别。远离原点的点P,其对应的瞬态尾流是由代表着类似Karman涡街的1、2阶模态所支配,这与二维柱体尾流是类似的;而原点附近的点P,其对应的瞬态尾流场中1、2阶模态的贡献可以忽略,此时的瞬态尾流场是由呈对称形态的3阶模态(如图 5所示)或更高阶模态所控制。图 8给出了上述两种典型的尾流状态,其对应P点的位置已在图 7(b)中标出。
 |
| 图 8 H/d=7柱体尾流中间高度截面内两种典型流动状态 Fig. 8 Two typical instantaneous flow status in the wake of prism with H/d=7 |
由上述分析可知,有限长柱体尾流会出现两种典型的瞬态流动结构:第一种是由1、2阶模态所控制的类似Karman涡街的形态,另一种是由3阶或更高阶 模态控制的对称形态。而在二维方柱尾流中,第二种形态是不会出现的。对于有限长棱柱体,当Karman涡街形态的尾流出现时,柱体侧面压力和柱体升力都会呈现出周期性显著的大幅波动;而当出现对称的尾流结构形态时,柱体侧面压力以及升力的脉动均较小,且无明显的周期性[1, 9, 25]。 3 结 论
(1) 代表着Karman涡街结构的1、2阶模态在H/d=7的有限场棱柱尾流中对湍动能的贡献为45.9%,远小于其在二维柱体尾流中对湍动能的贡献73.6%;而代表着对称形态的3阶模态对前者的贡献达到9.8%,是后者对应值的2倍多。
(2) 可以利用POD分析方法获得的1、2阶模态的系数(a1*,a2*),对有限长棱柱尾流的瞬态流动形态进行判断。其尾流中会出现两种典型的流动状态:一种是当1、2阶模态占主导地位时所对应的Karman涡街形态,此时类似于二维柱体尾流;另一种是当3阶或更高阶模态占主导地位时所对应的对称形态。这两种尾流形态的交替出现,使得有限长柱体所受气动力特性显著区别于二维柱体的对应情况。
| [1] | WANG H F, ZHOU Y. The finite-length square cylinder near wake[J]. Journal of Fluid Mechanics, 2009, 638: 453-490. |
| [2] | PARK C W, LEE S J. Free end effects on the near wake flow structure behind a finite circular cylinder[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 88: 231-246. |
| [3] | SUMMER D, HESELTINE J L, DANSEREAU O J P. Wake structure of a finite circular cylinder of small aspect ratio[J]. Experiments in Fluids, 2004, 37: 720-730. |
| [4] | ZDRAVKOVICH M M. Flow around circular cylinders(Vol 2): Applications[M]. Oxford: Oxford University Press, 2003. |
| [5] | WANG H F, ZHOU Y, CHAN C K, LAM K S. Effects of initial conditions on interaction between a boundary layer and a wall-mounted finite-length-cylinder wake[J]. Physics of Fluids, 2006, 18: 065106. |
| [6] | OKAMOTO T, SUNABASHIRI Y. Vortex shedding from a circular cylinder offinite length placed on a ground plane[J]. Journal of Fluids Engineering, 1992, 114: 512-521. |
| [7] | PATTENDEN R J, TURNOCK S R, ZHANG X. Measurements of the flow over a low-aspect-ratio cylinder mounted on a ground plane[J]. Experiments in Fluids, 2005, 39: 10-21. |
| [8] | KAWAI H, OKUDA Y, OHASHI M. Near wake structure behind a 3D square prism with the aspect ratio of 2.7 in a shallow boundary layer flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 104: 196-202. |
| [9] | SATTARI P, BOURGEOIS J A, MARTINUZZI R J. On the vortex dynamics in the wake of a finite surface-mounted square cylinder[J]. Experiments in Fluids, 2012, 52: 1149-1167. |
| [10] | RAFFEL M, WILLERT C, WERELY S, et al. Particle image velocimetry: a practical guide[M]. Berlin, Springer, 2001. |
| [11] | STERN F, MUSTE M, BENINATI L, et al. Summary of experimental uncertainty assessment methodology with example[R]. Iowa City, LA: Iowa institute of Hydraulic Research, The University of Iowa, 1999. |
| [12] | LYN D A, EINAV S E, RODI W, et al. A laser-doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder[J]. Journal of Fluid Mechanics, 1995, 304: 285-319. |
| [13] | OKAJIMA A. Strouhal numbers of rectangular cylinders[J]. Journal of Fluid Mechanics, 1982, 123: 379-398. |
| [14] | XIE L, JIN S Y, WANG Y Z, et al. PIV measurement and POD analysis of inner flow field in 90° bending duct of circular-section with fore-end valve[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(3): 21-25. 谢龙, 靳思宇, 王玉璋, 等. 阀体后90°圆形弯管内部流场PIV测量及POD分析[J]. 实验流体力学, 2012, 26(3): 21-25. |
| [15] | SIROVICH L. Turbulence and the dynamics of coherent structures[J]. Quarterly of Applied Mathematics, 1987, 45: 561-590. |
| [16] | YANG X, DING P, LI Z Y, et al. Extraction and analysis of turbulent large scales based on POD method[J]. Journal of Experiments in Fluid Mechanics, 2010, 30(06): 1019-1021. 阳祥, 丁鹏, 李增耀, 等. 基于POD方法的湍流大尺度信息提取与分析[J]. 工程热物理学报, 2010, 30(06): 1019-1021. |
| [17] | LI F H, NI Z H, SHEN S Z, et al. Theory of POD and its application in wind engineering of structures[J]. Journal of Vibration and Shock, 2009, 28(04): 29-33. 李方慧, 倪振华, 沈世钊, 等. POD原理解析及在结构风工程中的几点应用[J]. 振动与冲击, 2009, 28(04): 29-33. |
| [18] | ZOU Y, LIANG S G, ZOU L H. Reconstruction of fluctuating wind pressure field by applying POD of eigenvector correction[J]. China Civil Engineering Journal, 2010, 43: 305-309. 邹垚, 梁枢果, 邹良浩. 基于本征模态修正的POD法在风场重建中的应用[J]. 土木工程学报, 2010, 43: 305-309. |
| [19] | ZHOU F, NI Z H, XIE Z N. Prediction of wind pressure field on pitched roof using POD[J]. Chinese Quarterly of Mechanics, 2005, 26(2): 248-256. 周福, 倪振华, 谢壮宁. 利用POD对双坡屋盖风压场预测[J]. 力学季刊, 2005, 26(2): 248-256. |
| [20] | Van OUDHEUSDEN B W, SCARANO F, Van HINSBERG N P, et al. Phase-resolved characterized of vortex shedding in the near wake of a square-section cylinder at incidence[J]. Experiments in Fluids, 2005, 39: 86-98. |
| [21] | MEYER K E, PEDERSEN J M, ZCAN O. Turbulent jet in crossflow analyzed with proper orthogonal decomposition[J]. Journal of Fluid Mechanics, 2007, 583: 199-228. |
| [22] | MA X, KARNIADAKIS G E. A low-dimensional model for simulating three-dimensional cylinder flow[J]. Journal of Fluid Mechanics, 2002, 458: 181-190. |
| [23] | DING P, TAO W Q. Reduced order modeling with the properorthogonal decomposition[J]. Journal of Engineering Thermophysics, 2009, 30(6): 1019-1021. 丁鹏, 陶文铨. 建立低阶模型的POD方法[J]. 工程热物理学报, 2009, 30: 1019-1021. |
| [24] | DURAO D F G, HEITOR M V, PEREIRA J C F. Measurements of turbulent and periodic flows around a square cross-section cylinder[J]. Experiments in Fluids, 1988, 6: 298-304. |
| [25] | WANG H F, XU M X. Bistable phenomenon of the flow around a finite-length square prism[J]. Mechanics in Engineering, 2013, 35(3): 46-50. 王汉封, 徐萌霞. 有限长正方形棱柱绕流的双稳态现象[J]. 力学与实践, 2013, 35(3): 46-50. |