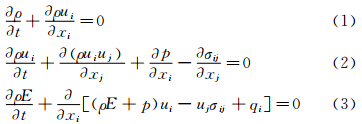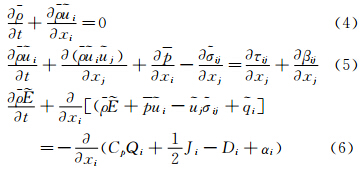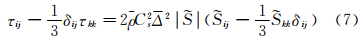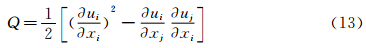钝体绕流包含丰富的物理现象,例如在低马赫数范围内存在流动的分离和再附、剪切层的失稳和转捩、周期性的涡脱落以及尾迹的发展;跨声速范围内会出现激波和涡、剪切层以及尾迹等的相互作用,尾迹中还会形成局部超声速区。对这些典型流动现象的研究不仅具有明确的科学意义,也有很高的工程价值。
作为两种基本的钝体几何形状,圆柱和矩形柱的绕流问题得到了大量的实验和数值研究。对于圆柱情形,不可压缩和可压缩绕流两方面的研究都比较充分,但针对矩形柱绕流的研究目前还仅限于不可压缩或者低马赫数的情形。Lyn等[1]利用水洞实验对雷诺数为21400的方柱绕流的流场做了全面的测量,为数值模拟方法的验证提供了参考。Grigoriadis等[2]采用浸没边界方法对方柱绕流进行了数值模拟,得到 了比较准确的trouhal数以及不同位置处的速度剖面。谢志刚等[3]采用有限体/有限元混合方法对雷诺 数为22000、马赫数为0.1的方柱绕流进行了大涡模拟,亚格子模式采用涡粘和涡扩散模式,并且将低马赫数预处理方法应用到了非定常流动的数值模拟中,数值模拟得到的回流区长度、恢复速度以及脉动量较以往的数值模拟结果都有较大改进。邓小兵等[4]利用虚拟压缩方法对三维方柱不可压缩绕流进行了大涡模拟,将雷诺数为22000时的主涡脱落频率、分离区长度、平均升力和平均阻力与实验数据做了对比,得到了较为满意的结果。Nakaguchi等[5]实验研究了不同雷诺数和不同长宽比的不可压矩形柱绕流的流动特性,结果显示在长宽比为0.6时,阻力系数达到最大值,长宽比为2.8时涡脱落频率不连续,该实验结果被后续的一系列相关研究[6, 7, 8, 9, 10]所证实。Bruno等[11]采用大涡模拟方法研究了长宽比为5 : 1的矩形柱绕流特性,观察到了柱体上表面发生流动分离和再附以及远离前缘点的上表面涡结构的三维特性。
下面介绍一下目前关于圆柱跨声速绕流的实验和数值研究。Murthy & Rose[12],Macha[13]和Rodriguez[14]实验研究了雷诺数为 105量级的圆柱跨声速绕流,结果表明流场中存在一些激波结构,跨声速范围内随着马赫数的增大阻力上升,马赫数高于0.9时周期性涡脱落消失。Miserda & Leal[15]采用有限 体积法计算了二维可压缩的avier-Stokes方程,对来流马赫数为0.8的圆柱绕流进行了数值模拟,主要研究了圆柱的受力和圆柱周围的流场结构。由于实验时非定常的数据测量存在一定的困难,而数值研究 大都求解欧拉方程,没有流场结构的细致分析,因此还有很多流动物理机制有待探索。Xu等[16]采用大 涡模拟方法求解了三维的可压缩N-S方程,研究了不同马赫数下圆柱跨声速绕流的流动特性,其研究表明,在跨声速范围存在一个临界马赫数(该马赫数约为0.9),当来流马赫数小于临界马赫数时,流动为非定常状态;当来流马赫数大于临界马赫数时,流动为准定常状态。通过对这两种不同流动状态的流动特性和相关物理机理的分析,研究了局部超声速区的形成机制、湍流剪切层的演化特性和不稳定性以及流场的湍流特性和涡结构等。矩形柱与圆柱绕流的不同点在于矩形柱是固定点分离,针对矩形柱跨声速绕流的流动特性还有待研究。
本文中,我们采用基于非结构网格的有限体/有限元混合格式和大涡模拟方法,对低亚声速和跨声速条件下的可压缩矩形柱绕流开展研究。我们主要关注矩形柱绕流的统计量、流动的分离和再附以及三维涡结构等,分别对低亚声速和跨声速情况下的流动特性作了分析,在跨声速情况下我们还考察局部超声速的形成及其物理机理。 1 控制方程和数值方法 1.1 控制方程
我们考虑可压缩流动的连续方程、动量方程,即Navier-Stokes (N-S) 方程和能量方程,形式如下:
式中ui表示速度分量,p=ρRT表示压强,其中ρ为密度,R为气体常数,T为温度,σij=2μ(Sij-Skkδij/3)为粘性应力张量,其中μ为动力粘性系数,Sij= 为变形率张量,E=CvT+uiui/2表示总能量,其中Cv为定容比热容,
为变形率张量,E=CvT+uiui/2表示总能量,其中Cv为定容比热容, 为热传导项,其中κ为热扩 散系数。
为热传导项,其中κ为热扩 散系数。
采用密度加权的Favre滤波方法,由式(1)~式(3)可得:
式中顶标“-”表示直接过滤操作,顶标“~”表示Favre过滤操作,即对任一物理量f和密度ρ,有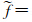
 。式(4)~式(6)中,
。式(4)~式(6)中, 可由Favre过滤的定义得出,即过滤后的状态方程,
可由Favre过滤的定义得出,即过滤后的状态方程, 表示总能量的过滤,包含了亚格子尺度的动能 k=
表示总能量的过滤,包含了亚格子尺度的动能 k=  和可解尺度的总能量
和可解尺度的总能量 。 在方程右端,
。 在方程右端, 为亚格子应力项,
为亚格子应力项, 为亚格子热传导项,Ji=
为亚格子热传导项,Ji= 为亚格子湍流扩散项,
为亚格子湍流扩散项,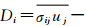
 为亚格子粘性扩散项,这些项均为未知项,需?捎醚歉褡幽J浇蟹獗铡1疚闹校颐遣捎肧magorinsky模型对亚格子偏应力项进行模化,即:
式中Cs为模式常数,
为亚格子粘性扩散项,这些项均为未知项,需?捎醚歉褡幽J浇蟹獗铡1疚闹校颐遣捎肧magorinsky模型对亚格子偏应力项进行模化,即:
式中Cs为模式常数, 为过滤尺度,
为过滤尺度, 。考虑到压缩性的影响,亚格子正应力项的模式可由亚格子能量平衡假设给出[17]:
式中CI为模式常数。亚格子热传导Qi采用涡扩散模式:
式中kt为亚格子热传导系数,采用下式确定:
式中
。考虑到压缩性的影响,亚格子正应力项的模式可由亚格子能量平衡假设给出[17]:
式中CI为模式常数。亚格子热传导Qi采用涡扩散模式:
式中kt为亚格子热传导系数,采用下式确定:
式中 表示亚格子涡粘系数,Prt表示湍流Prandtl数。其他的亚格子项,即亚格子湍流扩散项Ji和亚格子粘性扩散项Di都被忽略。另外,式(5)和式(6)中的αi和βij反映了直接过滤与Favre 过滤的差别,分别表示为
表示亚格子涡粘系数,Prt表示湍流Prandtl数。其他的亚格子项,即亚格子湍流扩散项Ji和亚格子粘性扩散项Di都被忽略。另外,式(5)和式(6)中的αi和βij反映了直接过滤与Favre 过滤的差别,分别表示为 ,通常在求解时直接被忽略。
1.2 数值方法
,通常在求解时直接被忽略。
1.2 数值方法本文采用基于非结构网格的有限体/有限元混合方法,即采用有限体积法计算对流通量、采用有限单元法计算粘性通量,在时间方向上利用四阶龙格-库塔方法进行推进。为此我们需要构造两套重合的网格,即有限体网格和有限元网格,如图 1所示,有限元单元为三角形(二维)或四面体(三维),在此基础上以每个节点为中心构造有限体单元,两套网格均覆盖整个计算域。
我们利用有限单元的形函数,可由单元节点上物理量的值得到其在单元内的分布及空间导数,进而求得有限体单元边界上的粘性通量。另一方面,对流通量的计算采用了Roe格式,其优点是能够捕捉激波并且不需要迭代。由于流动参数值存储在节点上(即有限体单元的中心),计算通量需要边界上的值,因此需要在有限体单元内进行数据重构。这里我们采用了 MUSCL插值,使得Roe格式具有空间二阶精度。为解决低亚声速情况下Roe格式引起的刚性问题,需要对数值方法进行预处理。上述方法在文献[3]中有详细的解释。此外,对于可压缩流动,Roe格式可能导致违反熵条件的非物理解,在激波附近引起数值不稳定。因此,在马赫数较高时,我们做了两方面的改进来抑制非物理解的产生。一是进行熵修正,即对对流项系数矩阵的特征值绝对值过小的情况进行限制;二是加通量限制器,本文中我们采用了基于非结构网格的WBAP限制器[18]。
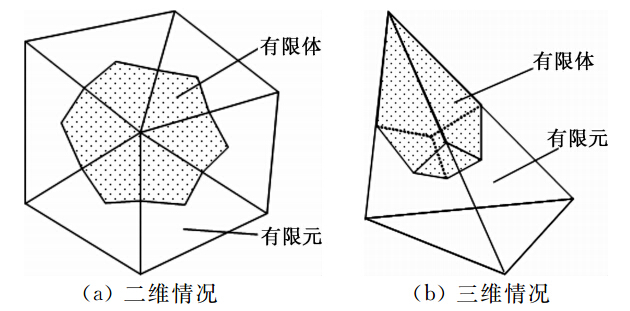 |
| 图 1 网格划分示意图 Fig. 1 Schematic of unstructured mesh |
本文的算例中,我们采用来流马赫数Ma=0.1和Ma=0.75,基于矩形柱高度和来流速度的雷诺数Re=22000,矩形柱长宽比分别取1 : 1,2 : 1,3 : 1和 4 : 1。当Ma=0.1时,计算域入口采用Steger-Warming通量条件 ,即利用矢通量分裂法计算从域外流入域内的对流通量,上下边界采用对称边界条件,出口采用基于特征线的无反射边界条件,展向采用周期边界条件,矩形柱表面采用绝热不可滑移条件。当Ma=0.75时,计算域入口、出口、上下边界都采用远场边界条件,展向采用周期边界条件,矩形柱表面采用绝热不可滑移边界条件。图 2为计算域、坐标系和网格分布示意图,矩形柱截面的宽度和来流速度分别用D和U∞表示。Ma=0.1时计算域流向(x)长度取为24D,矩形柱前端面距入口6.5D,计算域横 向(y)宽度H=14D,展向(z)宽度为4D,计算时间步长取 0.003D/U∞。Ma=0.75时计算域流向和横向长度均取36D,计算时间步长取为0.006D/U∞,其余不变。整个计算域采用非结构网格离散,柱体周围的网格最密,尺寸约为0.01D,尾迹中次之,远离柱体的地方网格最疏,如图 2所示。Ma=0.1时计算域总节点数为117158,总单元数为655662;Ma=0.75时总节点数为274424,总单元数为1571242。随着矩形柱长宽比的变化,总节点数和总单元数略有不同。
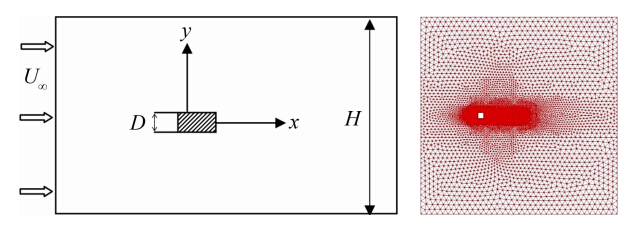 |
| 图 2 计算域、坐标系和网格示意图 Fig. 2 Computational domain,coordinates and mesh |
图 3和图 4 分别显示了矩形柱的阻力系数和升力系数脉动均方根随长宽比的变化,并和现有的低亚声速结果做了比较[10, 19]。从图中可以看出,低亚声速和跨声速时阻力系数都随着长宽比的变大而逐渐降低,跨声速时升力系数脉动均方根比低亚声速时小很多,说明湍流脉动受到抑制,可以从图 11显示的瞬时涡结构图像看出。
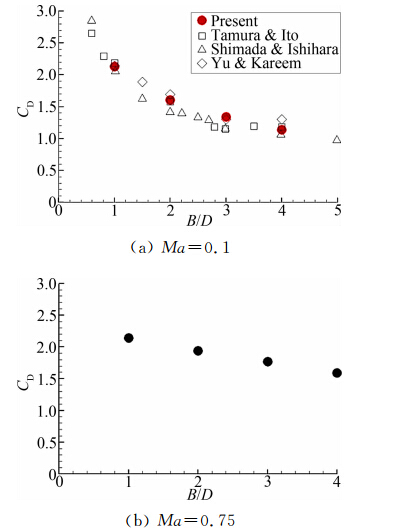 |
| 图 3 矩形柱的阻力系数随长宽比的变化 Fig. 3 Drag coefficient around rectangular cylinders with diferent aspect ratios |
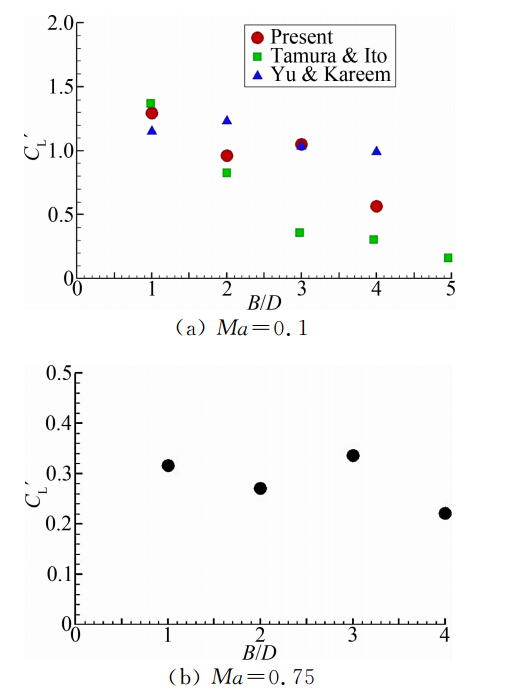 |
| 图 4 矩形柱的升力系数脉动均方根随长宽比的变化 Fig. 4 Lift coefficient RMS of rectangular cylinders with different aspect ratios |
流动的特征频率通常用Strouhal数反映,其定义为:
式中U∞无穷远处的来流速度,f为流动的频率,可以利用升力系数或流场中某点的压强信号的频谱得到。图 5显示了Ma=0.1时矩形柱绕流的Strouhal数随长宽比的变化,及其与文献结果的比较[9, 10, 19, 20],这里流动频率采用升力系数的频谱得到。可以看出,长宽比从1 : 1增大到2 : 1时,Strouhal数降低,而长宽比从2 : 1变为3 : 1时,Strouhal数有一个跳跃,出现两个主要的流动频率,之后长宽比再增大时,两个Strouhal数都逐渐减小。这种变化与矩形柱表面流体的分离与再附相关。当长宽比为1 : 1和2 : 1时,流体从前缘分离之后在柱体的上下表面没有产生再附,因而长宽比越大,涡脱落频率越小;在长宽比介于2 : 1和3 : 1之间时,流体分离之后产生再附,然后再分离,此时流动的两个频率分别对应从前缘分离和从再附点分离的流体产生涡脱落的频率,后者的值较大;之后随着长宽比的增大,再附点与矩形柱后缘角点的距离变大,涡脱落的频率也随之变小。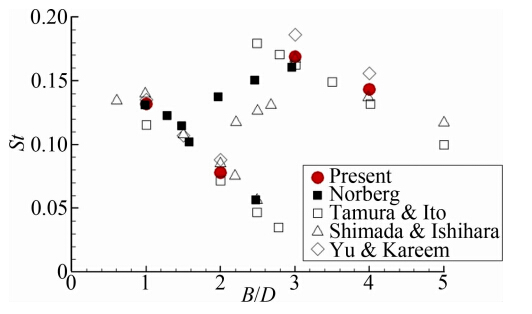 |
| 图 5 Ma=0.1时矩形柱绕流的Strouhal数随长宽比的变化 Fig. 5 Strouhal around rectangular cylinders with different aspect ratios at Ma=0.1 |
图 6表示Ma=0.75时矩形柱的Strouhal数随长宽比的变化,这里流动频率分别采用升力系数和特定点的压强信号的频谱得到,以显示流场的结构特征。由图可见,Strouhal数逐渐减小,其中采用升力系数和剪切层中的压强信号得到的Strouhal数相同,而矩形柱后中心线(y=0)上的压强信号则有两个不同的频率,分别为升力系数对应的Strouhal数的一半和两倍。由于柱体上下方的涡交替脱落,使得柱体后方中心线上流体的波动频率是涡脱落频率的两倍,而另一个小的频率表明存在长周期的运动,需要进一步研究。另外,当长宽比为4 : 1时,只有一个大的主导频率,小频率所对应的长周期流动结构很弱,因此在图中没有显示。
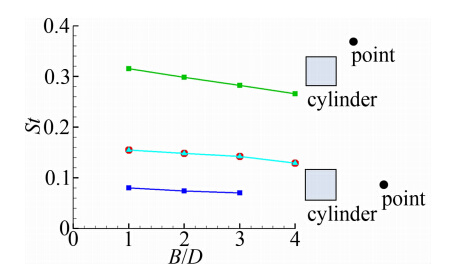 |
| ● 采用升力系数计算;▲ 采用剪切层中特定点的压强计算;□■ 采用矩形柱后中心线(y=0)上特定点压强计算 图 6 Ma=0.75时矩形柱绕流的Strouhal数随长宽比的变化 Fig. 6 Strouhal around rectangular cylinders with diferent aspect ratios at Ma=0.75 |
图 7显示了不同长宽比的矩形柱后中心线上流 向平均速度沿x方向的分布,原点对应矩形柱后驻点。图中负的极值点表示回流区的强度,随x增大的渐进值反映了恢复速度的大小。可以看出,Ma=0.1时,长宽比为2 : 1的回流最强,与前角点的分离 流在柱体表面发生再附有关。图中也显示了已有的 方柱绕流实验结果[1]作比较,可以看出回流区符合较 好,而恢复速度有一定程度的高估,这也是方柱绕流问题数值模拟中普遍存在的问题,具体原因还有待进一步分析。Ma=0.75时随着长宽比的增大,矩形柱后回流区速度峰值单调变小,而出口恢复速度逐渐变大。
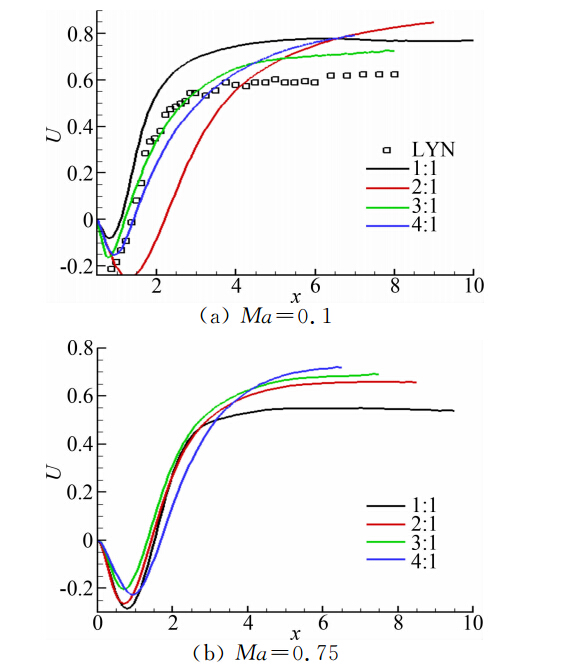 |
| 图 7 不同长宽比矩形柱后中心线上流向平均速度的分布 Fig. 7 Mean streamwise velocity U along the center line behind the rectangular cylinder with different aspect ratios at Ma |
压力系数Cp的定义为:
其中p 为平均压强,p∞为无穷远处压强,ρ∞无穷远处的密度。图 8显示了沿方柱表面从前驻点到后驻点 的Cp分布,横坐标s表示方柱表面某点到前驻点的 距离。可见,Ma=0.1时,方柱的压力系数最小,并 且随着长宽比的增大,矩形柱上表面的后缘以及背风面上压强逐渐增大,与长宽比增大后流体在矩形柱表面发生再附相关。Ma=0.75时变化更为单一,方柱的压力系数最小,随着长宽比的增大矩形柱上表面以及背风面上同样位置点的压强都逐渐增大,并且各矩形柱上表面的压强沿着s方向单调增加,柱体后缘角点处的压强最大。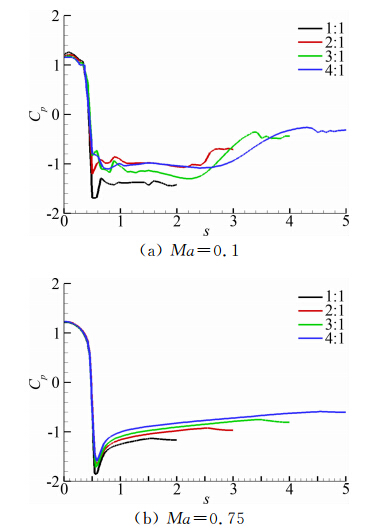 |
| 图 8 平均压力系数沿着不同长宽比的矩形柱表面的分布 Fig. 8 Mean pressure distribution on the surface of the rectangular cylinder with different aspect ratios at Ma |
图 9显示了不同长宽比矩形柱后中心线上流向 速度脉动均方根u′和横向速度脉动均方根v′沿x方向的分布。可以看出随着长宽比的增加,除了低亚声速情况下靠近柱体区域变化比较复杂,总体上流向和 横向的速度脉动均方根都逐渐减小。需要指出的是, 这里速度脉动为瞬时值与当地时均值之差,没有考虑周期性涡脱落的相位平均,所以图 9显示的脉动速度均方根可以反映涡的强度,但不能反映湍流脉动强度。因此,尽管在跨声速流动中湍流脉动受到抑制(如图 11所示),从图 9(a,b)和图 9(c,d)的对比中可以看到跨声速和低亚声速流动的脉动速度均方根为同一量级,结果与图 3显示的升力系数均方根有较大差 异。另外,由于柱体后方的展向涡结构会引起较大的横向速度,图 9(b,d)显示横向速度脉动均方根v′的 极大值位于2倍柱体宽度处,其值对应于柱体后方涡 脱落时离开柱体的距离,也大致相当于回流区的长 度,从后面的图 10和11可以看出。
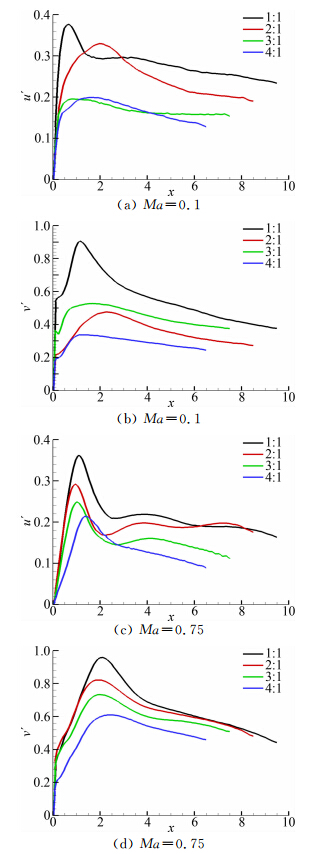 |
| 图 9 矩形柱后中心线上脉动速度均方根 u′和v′的分布 Fig. 9 RMS of velocity fluctuations u′ and v′ on the center line behind the cylinder |
 |
| 图 10 不同长宽比矩形柱平均流动的流线以及压强云图 Fig. 10 Streamline and pressure of mean flow around the rectangular cylinder with different aspect ratios |
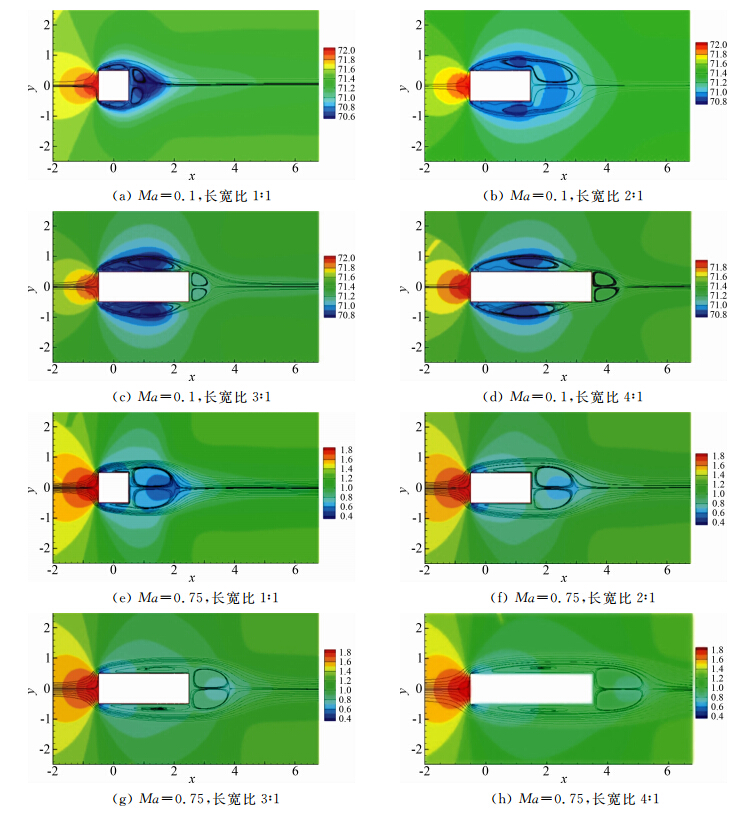
为了清楚显示不同长宽比矩形柱绕流是否再附,我们给出了平均流场的流线和压强分布,如图 10所示。可以看出,Ma=0.1时长宽比为3 : 1和4 : 1的矩 形柱有明显的再附点,流体从前缘点分离之后在柱体的上下表面发生再附,然后再与柱体分离。长宽比为 1 : 1和2 : 1的矩形柱则没有流动的再附现象发生。Ma =0.75时,流体从前缘分离之后并不会在柱体上下表面再附,并且随着长宽比的增大,尾迹里的低压区压强逐渐增大,从而使得阻力系数减小(见图 3)。
采用Q准则可以对流场的涡结构进行识别和显示,其定义如下:
图 11显示了不同长宽比矩形柱绕流的瞬时流场的Q等值面,Ma=0.1时Q=1.0,Ma=0.75时Q=0.1。可以看出,Ma=0.1时矩形柱尾迹里存在复杂的三维涡结构,而随着长宽比的增大尾迹里的涡逐渐变弱。Ma=0.75时,涡结构的三维 特性明显减弱,尾迹中存在强的展向涡形成 的涡街结构,近尾迹区连接两展向涡的流向涡结构。随着长宽比的增大,涡街中两展向涡间的流向距离逐渐变大,横向距离逐渐减小,当长宽比为4 : 1时,涡基本在排列一条直线上。
 |
| 图 11 不同长宽比矩形柱绕流的Q等值面 Fig. 11 Q contours around the rectangular cylinder with different aspect ratios |
尽管跨声速时钝体绕流的涡结构较为简单,但近尾迹区中也存在复杂的流动现象。Xu[16]指出圆柱跨声速绕流问题中,圆柱近尾迹区中存在两种形成机制不同的局部超声速区,分别为涡涡相互作用和涡与激波相互作用所形成。本文中我们考察了方柱跨声速绕流的近尾迹区的流动特征,发现也存在两种形成机制不同的局部超声速区。图 12给出了瞬时Ma=1的等值面,图中有两块单独的区域,分别记为A和B,其中A处是回流区中局部超声速区,B处为尾迹中形成的局部超声速区。
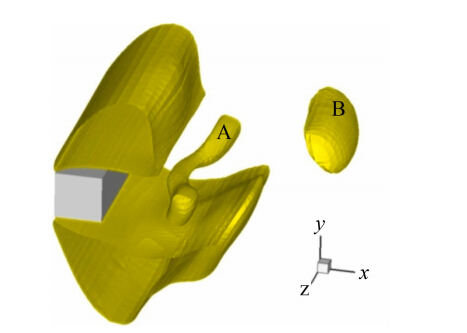 |
| 图 12 瞬时Ma=1的等值面 Fig. 12 Instantaneous Ma=1 contours |
为了观察局部超声速的形成过程,我们在Ma=0.75时方柱升力系数的时间演化曲线上选取了同一个涡脱落周期内的6个不同时间点a~f(见图 13),各时刻对应的马赫数等值线如图 14所示。可以看到,a时刻回流区内马赫数都小于1,超声速区并没有形成;b时刻在回流区中出现了M>1的一块小的区域,即局部超声速区;c时刻局部超声速区变大并且向下游移动,需要指出的是流动结构的迁移速度和当地流动速度不同,尽管局部超声速区位于回流区,仍然具有正的迁移速度;d时刻局部超声速区继续变大,并且要与上方剪切层中的超声速流体汇合,同时可以看到下方超声速剪切层从柱体脱落;e时刻前面所形成的局部超声速区已经完全与上方剪切层中的 超声速流体汇合,并且在方柱后不再有M>1的区域;f时刻出现新的M>1的区域,在随后的演化中将与下方剪切层中的超声速流体汇合,同时伴随着上方剪切层的脱落。因此,回流区中的局部超声速区形成后逐渐向下游迁移,然后与剪切层超声速流体汇合在一起,并逐渐与方柱分离。这里我们可以推断尾迹中形成的局部超声速区是由于超声速剪切层脱落而形成的。
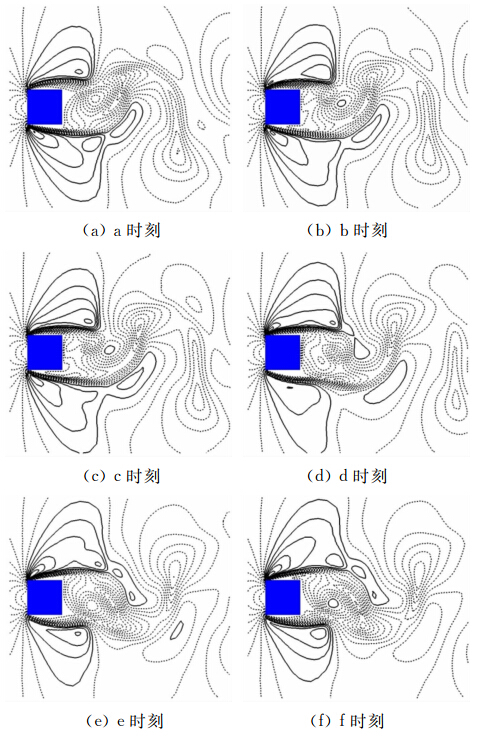 |
|
图 14 一个周期内不同时刻的马赫数等值线分布 (实线:M>1,虚线: M<1,时间间隔为0.3D/U∞) Fig. 14 Instantaneous iso-lines of Mach number with solid lines Ma>1 and dashed lines Ma<1,the time interval is 0.3D/U∞ |
为进一步分析回流区中的局部超声速区的成因,我们考察了b,e两个时刻(见图 13)的展向涡量和Ma=1的等值面,如图 15所示。可以看出,两个反 向旋转的涡的相互作用,使它们中间的流体加速,进而形成局部超声速区。由于对称性,回流区中的局部超声速区在每个涡脱落周期内形成两次,分别在方柱下方的涡向上运动和上方的涡向下运动时形成。
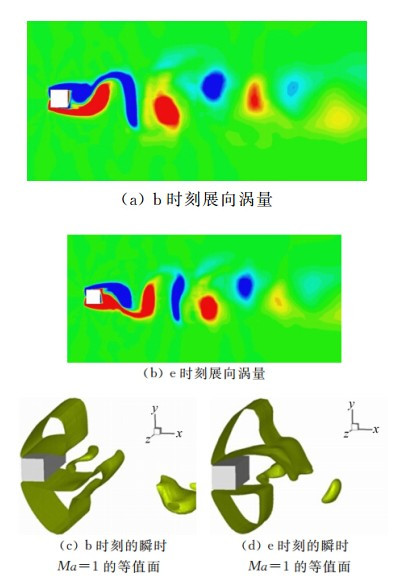 |
| 图 15 展向涡量云图和瞬时Ma=1的等值面 Fig. 15 Instantaneous spanwise vorticity and Ma=1 contours at the instants b and e |
本文采用有限体/有限元混合格式和大涡模拟方法求解可压缩N-S方程,研究了不同长宽比矩形柱低亚声速和跨声速绕流的流动特性。低亚声速范围内采用低马赫数预处理与MUSCL插值重构,跨声速范围内采用熵修正和WBAP通量限制器,时间推进格式采用四阶龙格-库塔方法。雷诺数为22000,来流马赫数分别取0.1和0.75,截面长宽比为1 : 1、2 : 1、3 : 1和4 : 1。研究表明:
马赫数为0.1时,Strouhal数随着长宽比的增大先降低再增大然后再降低;长宽比为3 : 1和4 : 1时柱体表面会有流动的再附产生;涡结构具有明显的三维特性。
马赫数为0.75时,Strouhal数随着长宽比的增大逐渐减小;湍流脉动以及涡脱落受到抑制;方柱的近尾迹区域中有两种形成机制不同的局部超声速区。
| [1] | LYN D A, EIVAN S, RODI W, et al. A laser-doppler velocimetry study of the en semble-averaged characteristics of the turbulent wake of a square cylinder[J]. Journal of Fluid Mechanics, 1995, 304: 285-319. DOI: 10.1017/S0022112095004435 |
| [2] | GRIGORIADIS D G E, BARTZIS J G, GOULAS A. LES of the flow past a rectangular cylinder using the immersed boundary concept[J]. International Journal for Numerical Methods in Fluids, 2003, 41: 615- 632. DOI: 10.1002/fld.458 |
| [3] | 谢志刚, 许春晓, 崔桂香, 等. 方柱绕流大涡模拟[J]. 计算物理, 2007, 24(2): 171-180. |
| [4] | 邓小兵, 张涵信, 李沁. 三维方柱不可压缩绕流的大涡模拟计算[J]. 空气动力学学报, 2008, 26(2): 167-172. |
| [5] | NAKAGUCHI H, HASHIMOTO K, MUTO S. An experimental study on aerodynamic drag of rectangular cylinders[J]. Journal of Japan Society of Aeronautic Space Science, 1968, 16: 1-5. |
| [6] | LAROSEG L, AUTEUIL A D. Experiments on 2D rectangular prisms at high Reynolds numbers in a pressurized wind tunnel[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 923-933. DOI: 10.1016/j.jweia.2007.06.018 |
| [7] | SHADARAM A, FARD M and ROSTAMY N. Experimental study of near wake flow behind a rectangular cylinder[J]. American Journal of Applied Sciences, 2008, 5 (8): 917-926. |
| [8] | TAYLOR I, VEZZA M. Prediction of unsteady flow around square and rectangular section cylinders using a discrete vortex method[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 82: 247-269. DOI: 10.1016/S0167-6105(99)00038-0 |
| [9] | SHIMADA K and ISHIHARA T. Application of a modified k-ε model to the prediction of aerodynamic characteristics of rectangular cross-section cylinders[J]. Journal of Fluid and Structures, 2002, 16: 465-485. DOI: 10.1006/jfls.2001.0433 |
| [10] | YU D, KAREEM A. Parametric study of flow around rectangular prisms using LES[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 77-78: 653-662. DOI: 10.1016/S0167-6105(98)00180-9 |
| [11] | BRUNO L, FRANSOS D, COSTE N, et al. 3D flow around a rectangular cylinder: a computational study[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98 : 263-276. DOI: 10.1016/j.jweia.2009.10.005 |
| [12] | MURTHY V S, ROSE W C. Detailed measurements on a circular cylinder in cross flow[J]. AIAA Journal, 1978, 16(6): 549-550. DOI: 10.2514/3.60930 |
| [13] | MACHA J M. Drag of circular cylinders at transonic Mach numbers[J]. Journal of Aircraft, 1977, 14(6): 605-607. DOI: 10.2514/3.58828 |
| [14] | RODRIGUEZ O. The circular cylinder in subsonic and transonic flow[J]. AIAA Journal, 1984, 22(12): 1713-1718. DOI: 10.2514/3.8842 |
| [15] | MISERDA R F B, LEAL R G. Numerical simulation on the unsteady aerodynamic forces over a circular cylinder in transonic flow[R]. AIAA 2006-1408. |
| [16] | XU C Y, CHEN L W, LU X Y. Effect of Mach number on transonic flow past a circular cylinder[J]. Chinese Science Bulletin, 2009, 54(11): 1886-1893. DOI: 10.1007/s11434-009-0325-x |
| [17] | YOSHIZAWA A, Statistical theory for compressible turbulent shear flows, with the application to subgrid modeling[J]. Phys. Fluids, 1986, 29: 2152-2164. DOI: 10.1063/1.865552 |
| [18] | LIW A, REN Y X, LEI G D, et al. The multi-dimensional limiters for solving hyperbolic conservation laws on unstructured grids[J]. Journal of Computational Physics, 2011, 230: 7775-7795. DOI: 10.1016/j.jcp.2011.06.018 |
| [19] | TAMURA T, ITO Y. Aerodynamic characteristics and flow structures around a rectangular cylinder with a section of various depth/breath ratios[J]. Journal of Structural and Construction Engineering (Transactions of Architectural Institute of Japan), 1996, 486: 153-162. |
| [20] | NORBERG C. Flow around rectangular cylinders: pressure forces and wake frequencies[J]. Journal of wind Engineering and Industrial Aerodynamics, 1993, 49: 187-196. DOI: 10.1016/0167-6105(93)90014-F |