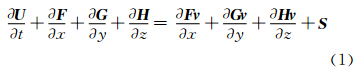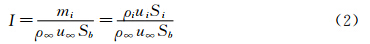导弹、炮弹等飞行器以超声速飞行时,气流在飞行器头部产生激波从而产生激波阻力,接着气流在飞行器底部发生大分离,形成低速、低压的回流区,在飞行器底部与头部形成较大的压力差,从而产生底部阻力。底部排气减阻的原理是向底部低压区排入低动量高温气体,改变底部流场结构,达到提高底部压力、减小阻力、增大射程的目的[1]。底排减阻增程技术主要用于超声速飞行的炮弹中(底部排气增程弹)。国内在20世纪90年代对底排增程技术进行了大量研究,取得了突出的成绩,为国内底排增程技术的发展奠定了基础。近年来,国内底排增程技术的研究基本 处于停滞状态。目前国内典型底排减阻增程弹的增程率约30%,这与国外的40%~50%存在着一定的差距,因此再次深入研究底排增程技术是很有必要的。
国内外对底部排气弹做了大量的数值研究[2, 3, 4, 5, 6, 7]。其中,国内数值研究底部排气弹全部采用量热完全气体的Navier-Stokes方程组求解流场,即认为底部排的是冷或者热空气,与外流空气属于同一种介质。这显然与真实的底部排气弹存在很大差异。真实的底部排气弹底部排气装置内高度贫氧的能源物质燃烧后会产生多种组分的混合气体,并且混合气体中含有一定量的富燃气体(CO+H2),这些富燃气体排出后与来流新鲜空气接触并发生二次燃烧,继续释放热量。文献[1]中明确指出采用底排真实气体与底排热空气进行底部排气减阻研究得到的一些结论有一定的差异,甚至有些结论完全相反。因此,为了更加接近实际情况,必须考虑底部排气为真实混合气体以及混合气体在底部流场中与来流新鲜空气发生的二次燃烧效应。国外仅有少数文献进行了底部排气弹底排真实气体的数值研究,并且没有研究攻角和船尾角对底排真实气体条件下的底部流场结构以及全弹气动特性影响。
本文考虑底部排气的真实气体效应,建立底部排气弹流动与燃烧模型,对底排真实气体条件下并考虑底部流场燃烧效应的底部排气弹全弹流场进行数值模拟,以更接近真实情况,拟得出底部排气弹底部流场结构与气动特性随攻角和船尾角的变化规律。 1 模型与方法 1.1 计算方法
在三维笛卡尔坐标系下微分守恒形式的雷诺时均(RANS)化学非平衡流Navier-Stokes方程为[8]:
其中 U为守恒变量,F、G、H为无粘对流通量,Fv、Hv、Gv为粘性通量,S为化学反应源项。湍流模型采用k-ωSST两方程湍流模型[9],化学动力学模型采用采用8组分(CO、H2、O2、CO2、H2O、H、OH、O)12个基元反应的CO-H2-O2系统化学反应模型[2]。考虑到超声速底部流场具有较强湍流特性,本文选择二阶矩湍流燃烧模型控制湍流-化学反应相互作用机理[10]。空间离散采用三阶MUSCL重构方法和AUSMPW+[11]迎风格式,粘性项采用中心格式离散,时间离散采用单步推进,并采用局部时间步长法加速收敛。在求解带化学反应的Navier-Stokes方程时,采用时间算子分裂的方法来处理刚性问题,即把求解流动偏微分方程时采用的时间步长进一步细分,作为求解化学反应刚性常微分方程的步长,计算化学反应对流场的贡献。 1.2 物理模型
本文在研究攻角对底部排气弹影响时均采用无船尾角、弹径为155mm的SOC炮弹作为研究对象。由于研究的炮弹为旋成体,为节省计算量,取全弹的一半为计算区域,且周向分布36个网格。此外,炮弹尾迹区湍流流动特性较强,需要对尾迹区网格进行加密,计算网格如图 1所示。在研究船尾角对底部排气弹影响时采用对原SOC弹增加不同船尾角并重新划分网格的模型作为研究对象。
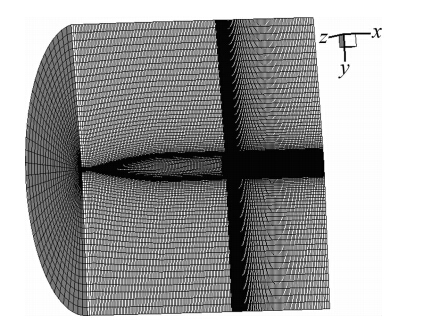 |
| 图 1 底部排气弹的三维计算网格 Fig. 1 The 3D computational grid of base bleed projectile |
底部排气弹表面采用无滑移非催化壁面条件。计算区域的外边界采用远场边界。底部排气弹的底部排气口处采用亚音速入口边界,并且给定排气参数I和排气总温T0。排气参数是底排装置排气质量流率与炮弹迎面空气质量排开率之比,数学定义式为:
式中下标“i”表示排气界面的物理参数,mi为排气质量流率,Si和Sb分别表示排气口面积和弹底面积,令Si/Sb为排气面积之比。本文第3节计算中均取排气面积比为0.1,排气总温为2000K,来流马赫数为2.5,以及相同的排气组分与质量分数。底排真实气体的主要组分和质量分数与文献[2]提供的数据保持一致,如表 1所示。| CO | H2 | CO2 | H2O | N2 |
| 0.3402 | 0.0241 | 0.3228 | 0.1627 | 0.1502 |
算例一:球头激波诱导燃烧[12, 13]。模拟的工况为来流马赫数是5.08,静温是291.5K,来流速度是2705m/s,静压是24797Pa,球头半径是7.5mm,来流气体为H2/O2混合物(2H2+O2),H2-O2反应系统的化学反应模型采用7组分8步基元反应模型。图 2和图 3为驻点线上压力、温度、主要组分质量分数分布,与参考文献数值模拟结果基本吻合。
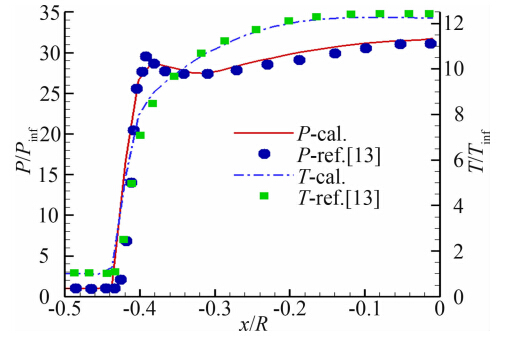 |
| 图 2 驻点线上压力与温度的分布 Fig. 2 Distribution of pressure and temperature along the stagnation streamline |
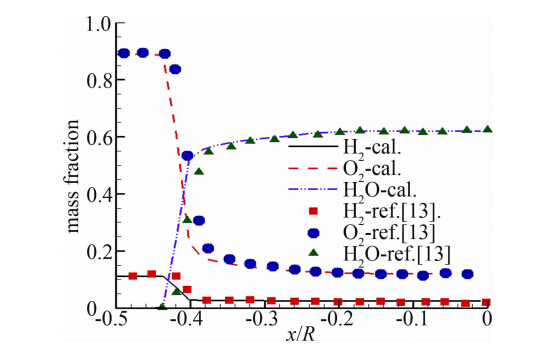 |
| 图 3 驻点线上主要组分质量分数的分布 Fig. 3 Distribution of main mass fraction along the stagnation streamline |
算例二:SOCBT炮弹带攻角飞行条件下表面压力分布[14]。来流马赫数3.0,攻角10.4°。计算结果如图 4所示。计算得到迎风面与背风面的表面压力(无量纲)分布与实验结果吻合较好,说明了本文建立的超声速炮弹气动特性CFD分析方法是有效的。
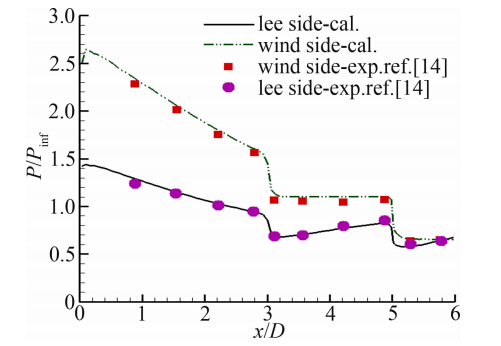 |
| 图 4 SOCBT炮弹背风面与迎风面的压力分布 Fig. 4 Distribution of pressure along leeward side and windward side |
为了更加清楚了解超声速底部排气减阻原理,首 先给出了理论流场结构示意图,如图 5所示。超声速来流在弹 底发生膨胀,气流压力降低,通过自由剪切层的传输,整个底部流场压力均低于远场来流的静压。而在底部喷入低动量(亚声速)的高温气体能改变底部流场结构,抬高自由剪切层的位置,降低超声速来流的膨胀程度,从而提高底部流场的压力,减小底部与头部的压力差,达到减小弹体底部阻力的目地。
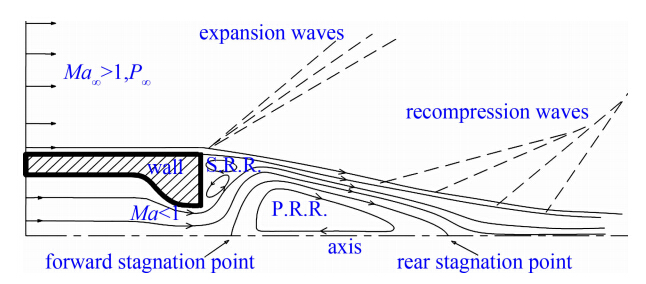 |
| 图 5 底部排气流场示意图 Fig. 5 Schematic representions of the flow field of base bleed |
图 6给出了排气参数为0.002、攻角为6.0°时的 全弹马赫数云图和压力(无量纲)云图。由图可以看出,在有攻角条件下,全弹流场表现出明显的不对称。在头部处,背风面的斜激波弱与迎风面。这是因为在有攻角条件下,相对于迎风面来说,自由来流在背风面的流动压缩角较小,产生的斜激波也相对较弱。总之,整个流场结构符合空气动力学规律,再次验证了本文计算方法的可靠性。
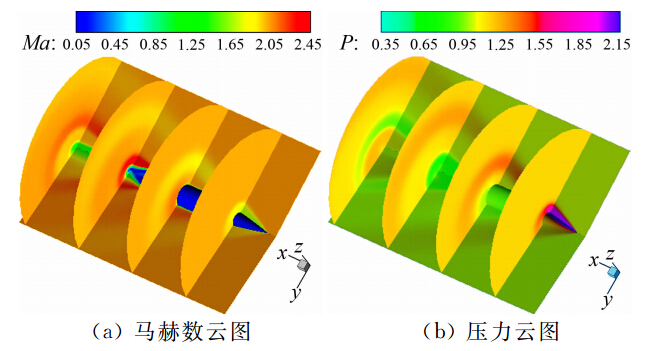 |
| 图 6 炮弹流场云图 Fig. 6 Contours of totalflow field around the projectile |
本节对攻角为0°、2°、4°、6°,无底排(I=0)、有底排(I=0.002、0.004)时的流场分别进行了计算与比较,由于篇幅有限,仅给出部分重要计算结果。
图 7~图 9分别给出了排气参数为0(无底排)、0.002、0.004时不同攻角下的底部对称面(Z=0 平面)流线图。由图 7可以看出,在无攻角飞行时,底部排气弹底部流动呈对称性。当有攻角飞行时,底部流动表现出明显的不对称,弹丸背风面(Lee Side)弹底的流动偏转角显著大于弹丸迎风面(Wind Side), 背风面的自由来流穿过底部轴线而流向迎风面。随着攻角的不断增大,迎风面和背风面的初始回流区体 积不断减小,且迎风面的初始回流区体积更小于背风面的初始回流区体积。
 |
| 图 7 I=0时底部对称面上流线图(无底排) Fig. 7 Streamline of the bottom symmetric plane at I=0(no base bleed) |
由图 8可以看出,在有底排条件下存在初始回流区和第二回流区。在无攻角条件下,流场结构对称。随着攻角的增大,迎风面和背风面的初始回流区体积逐渐减小,且迎风面的初始回流区体积始终小于背风区,当攻角为4°时,迎风面的初始回流区消失;迎风面的第二回流区体积逐渐减小,而背风面第二回流区体积逐渐增大。还可以看出,随着攻角的增大,底排气体从排气口排出后,较多的排气偏向背风面。这是由于在有攻角情况下,自由来流在背风面弹底拐点处的膨胀角较大,背风面弹底附近的压力也相应较小,排出的气体自然也就较多的偏向背风面。
 |
| 图 8 I=0.002时底部对称面上流线图 Fig. 8 Streamline of the bottom symmetric plane at I=0.002 |
图 9中的底部流场变化趋势与图 7和图 8相似。在该排气参数条件下,对应着较大的底部排气质量流率,初始回流区被后推更远,在弹底附近出现了第二回流区和第三回流区。
 |
| 图 9 I=0.004时底部对称面上流线图 Fig. 9 Streamline of the bottom symmetric plane at I=0.004 |
图 10、图 11分别给出了排气参数为0.002、0.004时不同攻角条件下底部流场温度等值线图。由图可以看出,攻角对排气参数I=0.002时的底部温度分布影响较大,而对排气参数I=0.004时的底部流场温度分布影响较小。结合图 8和图 9的流线图分析可知,虽然飞行攻角能严重影响底部流场的初始回流区而导致整个底部流场结构破坏,但是当排气参数增大时,底部初始回流区体积减小,飞行攻角对底部流场结构影响相应地减弱,即对底部流场温度分布影响较小。由图还可以看出,离弹底越远,流场温度越低。这是由于底排高温气体与外流冷空气混合所致。还可以发现整个底部流场温度并不高。这是由于底部排出的高温富燃气体中H2和CO的量较小,外流空气温度较低,两者接触混合后温度并不高,并且底部流场压力较低。因此在底部流场中发生的化学反应即富燃气体的二次燃烧是很微弱的,不同于在火箭发动机内流中高温高压燃烧,二次燃烧不能大幅度提高流场温度。
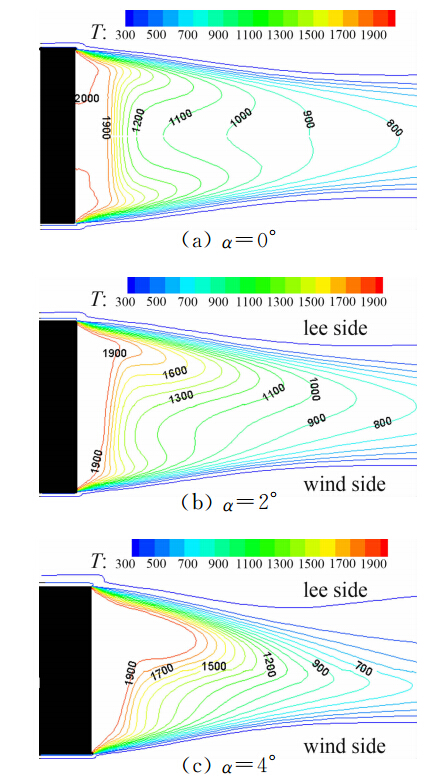 |
| 图 10 I=0.002时底部对称面上温度等值线图 Fig. 10 Temperature contours of the bottom symmetric plane at I=0.002 |
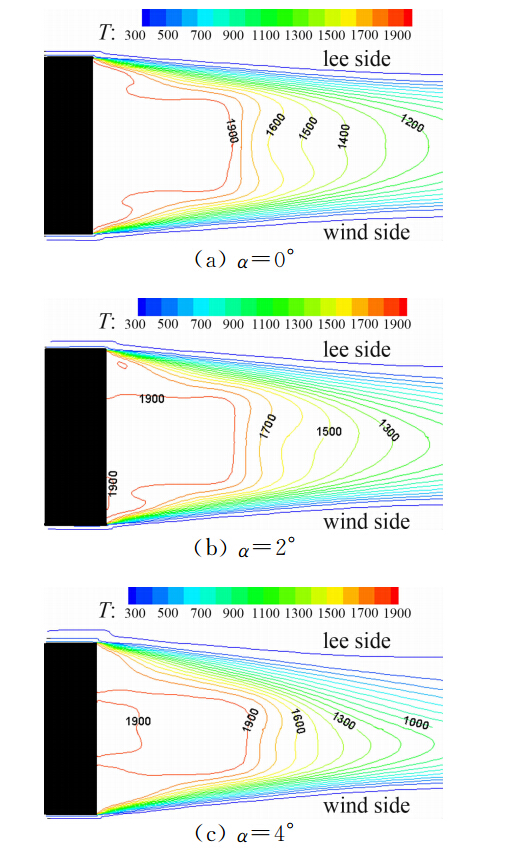 |
| 图 11 I=0.004时底部对称面上温度等值线图 Fig. 11 Temperature contours of the bottom symmetric plane at I=0.004 |
图 12、图 13分别给出了底部阻力系数、全弹总阻力系数随攻角变化的关系。由图可以看出,在不同排气参数条件下,随着攻角的增大,底部阻力系数与全弹总阻力系数均增大。这说明了带攻角飞行不仅增大了全弹总阻力,同时也通过改变底部流场结构而 导致底部排气的减阻效果变差。还可以看出,随着排气参数的增加,底部排气的减阻作用更加明显。在无攻角时,由底部阻力系数和全弹阻力系数可以计算得到排气参数I=0.002时的底部减阻率为28.6%,全弹减阻率为18.5%,而I=0.004时的底部减阻率为40.3%,全弹减阻率为26.7%。由此可见,增大排气 参数可以减小底部阻力系数与全弹总阻力系数,从而 增大减阻率。需要说明的是,本文研究的排气参数均处于底部排气减阻范围内,即处于小排气参数范围,排气的速度较低,没有以高速射流形式破坏底部流场结构。排气参数与减阻效果的关系较为复杂,具体可参考相关文献,这里不再叙述。
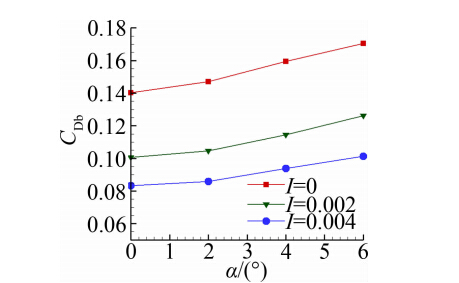 |
| 图 12 底部阻力系数与攻角的变化规律 Fig. 12 Base drag coefficients variation with attack angle |
 |
| 图 13 全弹总阻力系数与攻角的变化规律 Fig. 13 Total drag coefficients variation with attack angle |
图 14、图 15分别给出了升力系数、俯仰力矩系数随攻角的变化关系。由图可以看出,随着攻角的增大,升力系数与俯仰力矩系数呈线性增长趋势。升力系数与俯仰力矩系数基本不随排气参数变化,这是由 于升力与俯仰力矩主要由弹身产生,而底部排气仅作用于弹体底部,不会改变全弹弹身的流场结构。因 此,底部排气对于全弹的升力系数与俯仰力矩系数的 影响可以忽略不计。
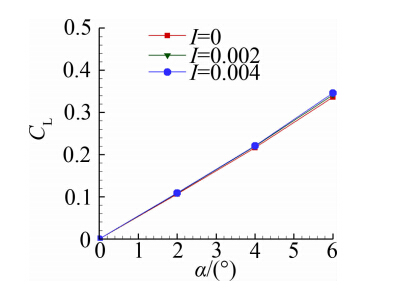 |
| 图 14 升力系数与攻角的变化规律 Fig. 14 Lift coefficients variation with attack angle |
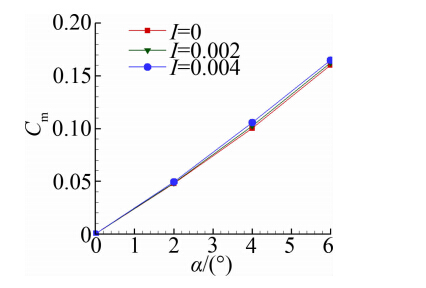 |
| 图 15 俯仰力矩系数与攻角的变化规律 Fig. 15 Pitch moment coefficients variation with attack angle |
船尾角减阻技术是飞行器减阻方法之一[15],合理选取船尾角是船尾角减阻技术的关键。本节数值研究了不同船尾角对底部流场结构以及全弹总阻力系 数的影响规律,且来流无攻角,船尾长为弹体圆柱段直径D。带有船尾角的弹体底部结构如图 16所示。
 |
| 图 16 炮弹船尾角示意图 Fig. 16 Schematic representions of boattail afterbody of projectile |
图 17给出了排气参数I=0.002、不同船尾角下底部对称面上温度等值线与流线图。由流线图可以看出,随着船尾角的增大,初始回流区体积逐渐减小,第二回流区逐渐减小并消失。由温度等值线图可以看出,随着船尾角的增大,底部富燃气体的二次燃烧程度增大,燃烧温度逐渐升高,流场中高温区分布范围扩大。还可以看出燃烧主要区域发生改变:当船尾角较小时,弹底有效面积较大,足以形成二次回流区,燃烧主要发生在该区域附近。当船尾角较大时,弹底有效面积较小,不足以形成二次回流区,燃烧主要发生在富燃气体与初始回流区相遇处附近的区域。
 |
| 图 17 不同船尾角下底部对称面上温度等值线与底部流线图 Fig. 17 Temperature contours and streamline ofthe bottom symmetric plane variation with boattail angle |
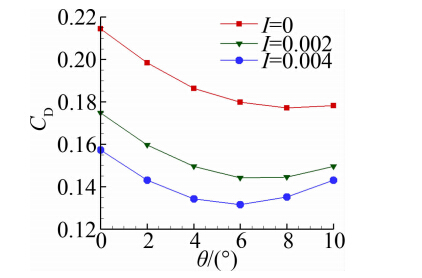
图 18给出了全弹总阻力系数随船尾角的变化规律。由图可以看出,在无底排I=0.0、排气参数I=0.002和排气参数I=0.004条件下,全弹总阻力系数均随着船尾角的增大呈先减小后增大的趋势。相应全弹阻力系数最小的船尾角为最佳船尾角。当底部不排气时,最佳船尾角在8°左右,排气参数I=0.002时对应的最佳船尾角为7°左右,而排气参数 I=0.004对应的最佳船尾角为6°左右。由此可见,有 底部排气时对应的最佳船尾角比无底部排气时的最佳船尾角小;有底部排气时,排气参数越大,减阻效果越好,最佳船尾角越小。
 |
| 图 18 全弹总阻力系数与船尾角的变化规律 Fig. 18 Total drag coefficients variation with boattail angle |
根据底部流场特征分析,船尾角技术减阻机理是:自由来流在经过船尾的绕流后,在弹底拐点处的膨胀程度减弱,从而提高底部压力;船尾角技术减小了底部有效面积,从而减小暴露在低压区的弹底面积。这两方面均能使底部压差阻力减小,从而减小了阻力系数。然而,自由来流在船尾角起点处膨胀,整个船尾表面的气流静压低于自由来流的静压,从而引起新的压差阻力(即船尾阻力),增大阻力系数。因此船尾角有两个相反作用:减小底部阻力;引起新的船尾阻力。在小船尾角时,减小底部阻力作用占主导因素,而在大船尾角时,船尾阻力作用占主导因素。因此存在一个最佳船尾角,此时的全弹总阻力系数最小,达到最佳减阻效果。 4 结 论
本文数值研究了攻角和船尾角对底部排气弹底排真实气体的底部流场结构与气动特性影响规律。研究结果表明:
(1) 攻角对底部流场结构影响较大。随着攻角的增大,迎风面和背风面的初始回流区体积逐渐减小,且迎风面的初始回流区体积始终小于背风区;迎风面的第二回流区体积逐渐减小,而背风面第二回流区体积逐渐增大;底排气体排出后偏向背风面。
(2) 随着攻角的增大,底部排气弹的底部阻力系数、总阻力系数、升力系数和俯仰力矩系数均增大。
(3) 底部排气对升力系数和俯仰力矩系数基本无影响,但对底部阻力系数和全弹总阻力系数有较大影响;在一定排气参数范围内,随着排气参数的增大,底部阻力系数和全弹总阻力系数不断减小,有利于减阻,从而提高射程。
(4) 船尾角的改变会引起底部流场结构的变化,同时影响着富燃气体的二次燃烧区域与强度;有底部排气时对应的最佳船尾角比无底部排气时的最佳船尾角小;有底部排气时,排气参数越大,减阻效果越好,最佳船尾角越小。
| [1] | GUO X F. The exterior ballistics of base bleed projectile[M]. Beijing: Publishing Company of National Defence Industry, 1994.(in Chinese). 郭锡福. 底部排气弹外弹道学[M]. 北京: 国防工业出版社, 1994. |
| [2] | GIBELING H J, NIETUBICZ C J. Navier-stokes computations for a reacting, M864 base bleed projectile[R]. AIAA-93-0504, 1993. |
| [3] | KAURINKOSKI P. Computation of the flow of thermally perfect gas past a supersonic projectile with base bleed[R]. AIAA-96-3451, 1996. |
| [4] | CHOR J R, SHIN E, KIM C K. Numerical study of base bleed projectile with external combustion[R]. AIAA 2005-4352, 2005. |
| [5] | SAHU, JHEAVEY KAREN R. Numerical investigation of supersonic base flow with base bleed[R]. AIAA-95-3459, 1995. |
| [6] | CHEN X H, ZHOU Z C, HUANG H, et al. Numerical simulation of base bleed energy affecting aerodynamic performance of base bleed projectiles[J]. Acta Armamentarii, 2010, 31(4): 448-452.(in Chinese). 陈新虹, 周志超, 黄华, 等. 排气能量对底部排气弹气动特性影响的数值模拟[J]. 兵工学报, 2010, 31(4): 448-452. |
| [7] | WU X S, WANG D, GUO X F. N-S computation of supersonic flow about a projectile[J]. ACTA Aerodynamica Sinica, 1998, 16(2): 162-166.(in Chinese). 武晓松, 王栋, 郭锡福. 弹丸超声速绕流的Navier-Stokes模拟[J]. 空气动力学学报, 1998, 16(2): 162-166. |
| [8] | OUYANG S W, XIE Z Q,XU C G. High temperature air non-equilibrium flows[M]. Beijng: Publishing Company of National Defence Industry, 2001. (in Chinese). 欧阳水吾, 谢中强, 徐春光. 高温非平衡空气绕流[M]. 北京: 国防工业出版社, 2001. |
| [9] | MENTER F R.Two equation eddy viscosity turbulence models for engineering application[J]. AIAA Journal, 1994, 32(8): 1598-1605. |
| [10] | ZHOU L X. Multiphase turbulent reaction fluid dynamics[M]. Beijng: Publishing Company of National Defence Industry, 2002.(in Chinese). 周力行. 多相湍流反应流体力学[M]. 北京: 国防工业出版社, 2002. |
| [11] | KIM K H, KIM C, RHO O H. Accurate computation of hypersonic flows using AUSMPW+ scheme and shock-induced grid technique[R]. AIAA-98-2442,1998. |
| [12] | LEHR H F. Experiments on shock-induced combustion[J]. Aeronautica Acta, 1972, 17: 589-597. |
| [13] | YUNGSTER S, EB ERHARDT S, BRUCKNER A P. Numerical simulation of hypervelocity projectiles in detonable gases[J]. AIAA Journal, 1991, 29(2): 215-223. |
| [14] | REKLIS R P, STUREK W B. Surface pressure measurements on slender bodies at angle of attack in supersonic flow[R]. ARBRL-MR-02876,1978. |
| [15] | TRIFU O, SAVE G. Optimum axisymmetric boattailing for minimum base drag at supersonic-moderate hypersonic speeds[R]. AIAA-93-5046, 1 993. |