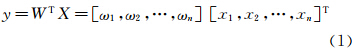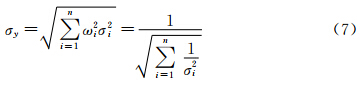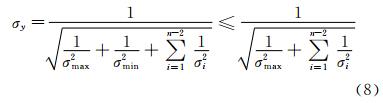2. 中国空气动力研究与发展中心, 四川 绵阳 621000
2. China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China
数据融合(Data Fusion)技术就是将来自不同途径的数据进行建模及综合处理，通过对多种测量手段的数据进行充分利用和合理支配，利用数据估计、建模、采集管理等手段，将这些测量结果在时间或空间上的冗余或互补信息依据某种准则来进行综合，产生被测对象更准确的信息、更一致的解释或描述，获得具有最大可信度的最优结果。按照这一定义，多测量系统是数据融合的硬件基础，多源信息是数据融合的加工对象，协调优化和综合处理是数据融合的核心，获得更准确的数据或更可靠的结论是数据融合的目的[1, 2, 3, 4]。
获取飞行器气动数据主要有风洞试验、数值计算和飞行试验(模型飞行试验)三种手段，各有其特点。风洞试验的数据精度高，但存在洞壁干扰、支架干扰、Re数、气动弹性、真实气体效应等影响，不能完全模拟真实飞行情况；数值计算的方便灵活，可获得精细的流场结构，但物理模型尚不够完善，计算精度有待进一步提高；飞行试验可以模拟真实飞行状态，但气动参数辨识结果的精准度受到发动机推力误差、传感器精度和大气扰动等影响，且飞行状态参数难以精确控制，试验数据有限，难以覆盖所有飞行状态。虽然获取准确可靠的气动力数据可以通过建设更先进的风洞、采用更高性能的数值模拟系统以及进行更多更精细的飞行试验，但在短时间内采用单一方式提高气动力数据精准度的程度有限，不能完全满足新一代飞行器研制的需要，而且将付出高昂的成本。而数据融合技术可以弥补这一缺陷，经过估算，两类同等精度的数据进行融合，融合后的精度可以提高30％～40％，即降低不确定度30％～40％。因此，数据融合技术在提高气动数据精准度方面具有很大的潜力。
对于某一飞行器外形，通过三种手段获得的气动数据是对同一对象采用不同方式获得的多源信息，三种来源信息具有冗余性和互补性，因此，从理论上讲，气动力数据融合是完全可行的。与一般信息的数据融合相比，气动力数据融合的难点在于：影响气动力预测误差的因素很多，而且影响过程复杂，数学描述困难；实际处理中面临的对象不同(数值计算—理论数模；风洞试验—风洞模型；飞行试验—全尺寸或缩比飞行模型)；气动力数据融合准则和方法有待进一步研究等。面对这些问题，本文探索性的研究了数据融合方法在空气动力学中的应用，在目前已有的工作基础上，综合提出了建立气动数据融合准则的基本思路和两种具有应用价值的融合算法：基于不确定度的数据融合方法和基于气动力建模的数据融合方法，并给出了部分研究应用结果。 1 国内外发展概况
1987年美国国会军事委员会把数据融合定为对其国防至关重要的21项技术之一，并在数据融合技术研究方面投入了巨额资金，目前在目标探测、识别、跟踪、导航定位、C3I系统等已广泛应用。国内数据融合技术研究起步较晚。到了80年代末才开始出现有关多传感器数据融合技术研究的报导，90年代初，这一领域逐渐形成高潮，发展成多方关注的共性关键技术。目前新一代舰载、机载、弹载和各种C4ISR系统正在向多传感器数据融合方向发展，在利用雷达、红外、可见光等多种异类信息融合方法研究方面取得了重要进展。
在气动数据融合研究领域，从公开发表的文章来看，国内外气动数据融合方法研究均处于起步阶段，尚未从数据融合研究的通用方法入手，即通过建立各种影响因素的误差传递模型开展数据融合研究。工程中目前常用的方法是假定一组气动数据精度较高，利用比例因子的方法，实现与精度较低气动数据的融合(例如，风洞实验数据与计算数据的融合，类似惯导与GPS的弹道融合)。该方法在高精度数据与低精度数据变化趋势一致的情况下取得较好的效果，但当二者变化趋势不一致时，则融合效果较差；另一类方法是利用神经网络方法，将计算数据和风洞试验数据进行融合，以达到提高气动数据精准度的目的[1, 2, 3, 4, 5, 6, 7, 8, 9]。
尽管气动数据融合技术在在国际上还未取得较大进展，但数据融合的思想已在航空航天发达国家气动研究中得到广泛的体现。如美国在航天飞机研制试验中[10]，通过对大量风洞试验(101个模型、约10万小时风洞试验的数据)、数值计算及多次飞行试验的数据进行综合分析，给出了综合三种手段的气动数据及不确定度，形成了“ADDB数据库”(航天飞机轨道器气动力设计数据手册)，在航天飞机研制、试验及后续应用中发挥了重要作用。NASA兰利研究中心和布朗大学曾合作针对波音757飞机主起落架开展了多轮风洞试验，试验手段包括油流显示、表面测压带和DPIV，针对不同试验手段获得的试验数据应用数据融合技术来获得精细的流动可视化结果[11]。NASA兰利研究中心和Dryden飞行研究中心合作，针对F-16XL-1飞机，进行飞行试验数据、风洞试验数据和CFD计算数据三者的融合比较，从而比较准确地获得了F-16XL-1飞机表面的流动情况[12]。NASA兰利研究中心还针对F/A-18飞机开展过同类数据融合技术研究，从而较好地修正了风洞试验结果[13]。近年来美国在发展“X”系列飞行器中，利用少量的飞行试验数据，通过与地面试验数据的融合，形成了具有工程实用性的工程数据库。前苏联(俄罗斯)在基于飞行器气动数据库和数据融合技术归纳建立气动特性快速估算方法、提炼参数影响规律等方面也取得了大量成果。
国内在气动数据融合准则、方法等方面的研究尚属于起步，但利用数据融合的思想和方法开展过一些应用研究。 2 气动数据融合准则与主要方法
数据融合技术的核心研究内容就是融合准则和算法研究。气动数据与常规传感器测量数据相比，有其自身的复杂性和特殊性，因此现有的数据融合准则和算法并不适用于气动数据融合，必须探索气动数据融合准则和算法，建立气动数据融合技术。
采用学科交叉的研究方法，由简单到复杂地开展研究。首先基于理论气动力数学模型的稳态行为分析与风洞试验数据的稳态模型拟合，建立反映气动力变化规律的气动力数学模型，根据气动力变化规律，采用满足气动力变化规律的程度作为气动力数据融合的准则，并采用期望极大化方法作为融合算法，探讨构建气动力数据融合算法的可行途径。
其次，借助于估计理论、控制论、优化方法和误差估计理论，借鉴数据同化的做法，深入研究多项式插值、经验性的连续修正法(Successive corrections method)、松弛法(Nudging)，优化插值(Optimal Interpolation)方法和现代数据同化方法(连续数据同化和顺序数据同化)，开展理论气动力数学模型的动态行为分析与 飞行试验数据的动态模型拟合以及基于动态模型参数拟合的理论气动力数学模型的参数修正方法研究，建立和完善气动力数据融合准则和方法。
下面给出数据融合的两种方法： 2.1 基于不确定度的数据融合
分别对不同来源的气动数据进行不确定度分析，再以所得出的不确定度作为权值参考进行加权融合，加权融合结果可作为最终的气动数据融合结果，如基于精度的加权平均数据融合方法，基于不确定度的加权平均数据融合方法可参照建立。 2.1.1 加权平均法进行数据融合时权对融合精度的影响[14, 15]
设对某个参数的测量有n个来源，第i个数据源输出的数据xi，其中i=1，2，…，n。由于各数据源的品质不同，而且受各种随机因素的干扰，xi具有随机性。在实际测量当中xi是服从正态分布N(μi，σi2)的，其中μi为期望值，它包含了被测参数的信息及该数据源的常值偏差；σi为均方差，代表该数据源的精度，σi值越大说明该数据源对同一参量测量时所得的数据离散度越大，即该数据源的精度越差；σi值越小该数据源的精度越高。
加权平均法是求各个数据源输出数据的加权平均值，若第i个数据源的输出为xi，其权为ωi，所有n个数据源输出数据的融合结果为：
用向量形式表示：W=[ω1，ω2，…，ωn]T，X=[x1，x2，…，xn]T，其中，W是权向量，X为输出向量。由于xi服从正态分布N(μi,σi2)，则经过如下变换: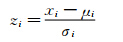
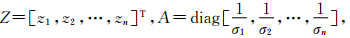U=[μ1，μ2，…，μn]T。
由式(2)得：X=A-1Z+U，代入式(1)得：
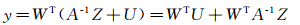
由多元统计理论可导出，y的分布密度函数服从正态分布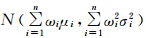
，表明经过融合后所得输出y的期望值为各数据源期望值的加权平均，精度为：
式(3)的值越小，表明融合后输出的精度越高。显然，在σi (i=1，2，…，n)一定的前提下，式(3)的值与权ωi (i=1，2，…，n)的分配密切相关。为了使y的精度达到最高，式(3)的值应该达到最小。那么，问题就归结为求条件极值的问题，即已知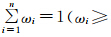
0,i=1,2,…,n)，σi(i=1，2，…，n)是已知数，求在ωi (i=1，2，…，n)满足什么条件时函数F(ω1，ω2，…，
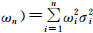的值最小。这是一个约束条件为等式的多变量条件极值问题，可用拉格朗日乘数法进行求解，具体解法如下。
引进修正函数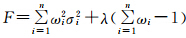
，对该函数分别求ωi (i=1，2，…，n)的偏导数
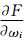。当
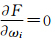(i=1，2，…，n)时函数F取得最小值，解方程组：
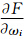=0可以得到所要求的条件，即：
由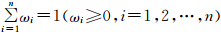
即可得：
将式(5)代入式(4)可得：
将式(6)代入式(3)可得多源数据融合后可达到的最高精度：
2.1.3 公式分析
假如几个数据源的精度相等，即：σ1=σ2=…=σn=σ，那么式(7)变为：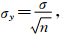
，表明n个相同精度数据源的输出数据融合后精度提高到单个数据源的n1/2倍。
假如几个数据源的精度有高低之分，最低精度与最高精度的均方根分别为σmin和σmax，则由式(7)得：
式(8)表明采用权的最优分配方法后，精度再差的数据源参与数据融合后都有利于提高测量的精度。这一点与其他方法有本质的区别。采用其他方法信息融合时，一个精度很差的数据源有可能使得融合结果精度变差。这一点具有非常重要的使用价值。图 1给出了采用该方法得出的某型无人机阻力系数融合结果和试验值比较。其中，带三角的为第一组试验值，带圆圈的为第二组试验值，实线为融合值。
 |
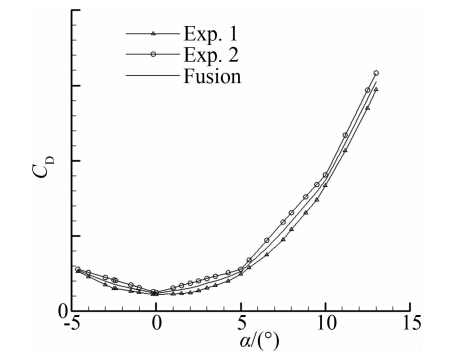| 图 1 阻力系数融合结果与试验结果的对比 Fig. 1 Comparison of drag coefficient between fusion data and experimental data |
如果风洞试验、数值计算、飞行试验状态存在较大差异，则不适合直接使用以上方法进行处理，需要先对不同来源的数据进行相关性分析，再进行融合。首先分析数值计算、风洞试验与飞行试验状态之间存在的具体差异，然后以CFD手段为主综合分析这些状态差异(如模拟外形、模拟状态、模拟参数等)引起的气动特性偏差量，利用得出的偏差量将三种手段得出的结果统一到相同状态，再利用前述方法进行分析融合。 2.2 基于建模的数据融合
由于飞行器气动特性的复杂性，对其进行描述的数学方法也不尽相同，总的来说可以分为两类，一类是具有明确物理意义的常规气动模型(如代数模型或积分方程模型)，另一类是基于响应面的气动模型(如神经网络模型、模糊逻辑模型等)。对于第一类气动模型，其数据融合过程为：模型建立后，以不同来源的气动数据为依据对该模型进行参数辨识，辨识完成后可以得出不同来源的气动数据与模型的拟合程度，由于模型包含有明确物理意义，与模型的拟合程度即是与实际物理规律的吻合程度，由此将拟合程度作为权值对多源气动数据进行加权融合。
文献[16]便是采用该种方法进行数据融合——通常可将气动力系数经验数学模型写为线性函数形式：
式中，y是因变量，xi是自变量，θi是待定参数，ε是随机误差，服从N(0,σ2)分布。首先用F检验方法对模型中的项进行筛选，然后利用筛选后模型对建模样本试验数据进行拟合，再计算拟合结果与试验数据之间的复相关系数，复相关系数越接近1，则模型与试验数据的相关性越强，模型反映气动力数据变化的规律性越好。
图 2给出了对某飞行器采用该方法得出的法向力系数融合结果与计算值和试验值比较。其中，带圆圈的为试验值，带‘＋’的为计算值，带菱形为融合值。
 |
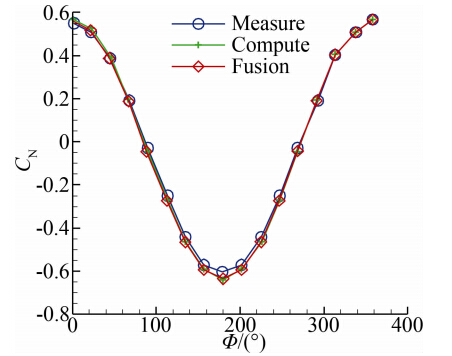| 图 2 法向力系数融合结果与试验和计算结果的对比 Fig. 2 Comparison of normal force coefficient among fusion data,experimental data and CFD data |
对于第二类响应面气动模型，其数据融合过程为：对不同来源数据分别建立响应面模型并计算建模结果与试验数据之间的复相关系数，然后以复相关系数作为加权因子，对不同来源的气动力数据进行融合处理。图 3中给出了针对某型导弹俯仰力矩系数采用神经网络建模的数据融合结果：其中圆圈为试验数据，三角为计算数据，实线为融合数据。
 |
| 图 3 数据融合结果与试验和计算结果的对比 Fig. 3 Comparison of pitching moment coefficient among fusion data,experimental data and CFD data |
可以说这两种方法的气动力数据融合准则都是：根据无论计算数据、风洞实验数据、还是飞行试验数据都必须满足气动力变化规律的原则，以成批(非单个)的气动力数据满足气动力变化规律(已体现在所建立的数学模型中)的程度为依据；某种来源的气动力数据满足气动力变化规律越好，则对融合结果的影响越大，反之，则越小[16]。
同时在将融合方法应用于具体飞行器气动数据融合之前，还需要对融合方法的适应性进行考核，包括两方面工作：一是用相关模型预测气动特性，利用原始数据考核预测结果的准度及误差范围；二是预测原始数据覆盖范围内的结果，通过补充部分试验及数值模拟进行验证。
本节介绍了气动数据融合的几种方法，每种方法所适用的范围不尽相同，具体采用何种方法还要结合自身气动数据的特点具体分析，不能一概而论。 3 气动数据融合和关联技术展望
气动数据关联和融合技术虽然在国外已经早有应用，如美国的航天飞机计划，并取得了较大的成功，但这项工作需要大量的工程经验，工作过程中也包括很多的主观人为因素，因此其中的细节仍然不得而知。我国目前尚在该项技术的研发阶段，由于没有成熟的经验可以借鉴，只能在摸索中前进，部分研究机构已经开始认识到了此项技术的重要性并进行了相关领域的尝试。如中国空气动力研究与发展中心与研制单位合作，曾经针对神舟飞船返回舱，在国内多家单位、多座风洞、不同阶段得到的大量风洞试验、计算数据及多次飞行试验基础上，通过对数据的综合分析与融合研究，形成了类似ADDB的返回舱气动设计数据库，首次建立了基于建模和不确定度的数据融合方法，取得了一定的研究成果。同时将该项技术应用于我国多个型号的飞行器设计中，并取得了较好的应用效果。通过对以往研究工作的总结，可以预计气动数据关联和融合技术至少在以下两方面会发挥比较重要的作用：(1) 通过数据分析和融合，可以对多组气动力风洞试验结果、计算结果和飞行试验结果进行融合，得到更加准确、更加全面的气动力数据，当然不同融合方法得出的结果会有所差异；(2) 通过数据融合方法反过来确定风洞及计算软件的不确定度，考虑历史数据和当前数据对结果的影响，可以进一步提高风洞试验和数值计算准确性，并有一定的预测能力。而这些工作都直接对飞行器的控制系统设计产生影响，并对最终飞行器性能产生影响，可以说该项技术对我国的飞行器设计总体水平的发展有着积极的作用。
总的来说，持续提高飞行器气动数据预测精准度，系统解决风洞试验、数值计算、飞行试验三种手段气动数据的相关性问题是飞行器空气动力研究与试验的长远目标，除通过建设更先进的风洞和大型数值模拟设备，发展更精细的试验、测试技术和计算方法外，利用数据融合技术具有很大的潜力和应用前景。本文对数据融合关联方法进行了介绍和梳理，通过对以往工作的总结，认为在以后的工作中还需要重点开展以下研究：
(1) 建立和完善具有普遍意义和工程应用价值的飞行器气动数据融合准则和方法；
(2) 改进传统的数据精准度评价方法，揭示试验数据一致性和重复性主要影响因素，建立风洞试验、数值计算、飞行试验数据不确定度评估方法；
(3) 三种手段紧密结合，系统开展气动数据融合研究及应用；
(4) 加强气动数据融合准则、方法的定量考核、验证研究，提高融合方法的适应性与融合结果的可信度。
相信，随着我国在气动数据融合和关联技术领域的发展，这一新兴技术必将为我国航空航天事业的发展提供更强大的推动力。
| [1] | LIU H, HU D Z. Development and applications of data mining technology[J]. Gansu Technology, 2006, 4: 73-75.(in Chinese). doi: 10.3969/j.issn.1000-0952.2006.04.028. 刘辉, 胡大治. 数据挖掘技术发展及其应用[J]. 甘肃科技, 2006, 4: 73-75. |
| [2] | WANG G H, JIANG P. Survey of data mining[J]. Journal of Tongji University, 2004, 32(2): 246-252.(in Chinese). doi:10.3321/j.issn:0253-374X.2004.02.023. 王光宏, 蒋平. 数据挖掘综述[J]. 同济大学学报, 2004, 32(2): 246-251. |
| [3] | WANG H Z, PENG A Q. Existing situation of data mining research and its development tendency[J]. Industry and Mine Automation, 2011, 2: 29-32.(in Chinese). doi: 32-1627/TP.20110124.1032.001. 王惠中, 彭安群. 数据挖掘研究现状及发展趋势[J]. 工矿自动化, 2011, 2: 29-32. |
| [4] | LIANG X X, LEI R H, CAO C X. Development in modern data- mining techniques[J]. Journal of Chongqing University, 2004, 27(3): 21-26.(in Chinese). 梁协雄, 雷汝焕, 曹长修. 现代数据挖掘技术研究进展[J]. 重庆大学学报, 2004, 27(3): 21-26. |
| [5] | GAO X, HOU X J. The technology of data mining[J]. Journal of Mudanjiang College of Education, 2008, 112(6): 109-110.(in Chinese). doi:10.3969/j.issn.1009-2323.2008.06.057. 高翔, 侯小静. 数据挖掘技术综述[J]. 牡丹江教育学院学报, 2008, 6: 109-110. |
| [6] | MARTINEZ-HERAS J A. Data mining at the service of space operations[R]. AIAA-2006-5717. doi:10.2514/6.2006-5717 |
| [7] | LIU Z Y, CHU W W. HUANG A. Mining sequence patterns from wind tunnel experimental data for flight control[R]. PAKDD 2001, LNAI 2035: 270-281. doi:10.1007/3-540-45357-1-30 |
| [8] | WALTZ E, LINAS T. Multi-sensor data fusion[M]. New York: Artech House, 1991. |
| [9] | YANG H, LI H. The technology of data fusion[J]. Mine Surveying, 2005, 9(3): 24-28.(in Chinese). doi:10.3969/j.issn.1001-358X.2005.03.009. 杨华, 林卉. 数据融合的研究综述[J]. 矿山测量, 2005, 9(3): 24-28. |
| [10] | Aerodynamicdesign data book Vol. 1 orbiter vehicle STS-1[R]. SD72-SH-0060 Volume 1, Rockwell International, 1980. |
| [11] | SEVERANCE K, BREWSTER P, LAZOS B, et al. Wind tunnel data fusion and immersive visualization: a case study[A]. In: Proceedings of IEEE Visualization 2001[C]. San Diego: IEEE Computer Society, 2001: 505-508. doi:10.1109/VISUAL.2001.964563. |
| [12] | LAMARJ E, O BARA C J, FISHER B D. Flight, wind-tunnel, and computational fluid dynamics comparison for cranked arrow wing(F-16XL-1) at subsonic and transonic speeds[R]. NASA TP-2001-210629. |
| [13] | GHAFFARI F. Navier-Stokes, flight, and wind tunnel flow analysis for the F/A-18 aircraft[R]. NASA TP-1994-3478. |
| [14] | HE Y, WANG G H, LU D J, et al. Multi-sensor information fusion and application[M]. Beijing: Publishing House of Electronics Industry, 2000.(in Chinese). 何友, 王国宏, 陆大金, 等. 多传感器信息融合及应用[M]. 北京: 电子工业出版社, 2000. |
| [15] | LI X L, SUN Y, MOH W. Research on data fusion algorithm of redundancy information based on least square method. Computer Engineering and Applications, 2009, 45(15): 34-38.(in Chinese). doi:10.3778/j.issn.1002-8331.2009.15.010 李雪莲,孙尧,莫宏伟. 基于最小二乘法的冗余信息数据融合算法实现[J]. 计算机工程与应用, 2009, 45(15): 34-38. |
| [16] | WANG W Z, GUI Y W, HE K F, et al. Aerodynamic data fusion technique exploration[J]. ACTA Aerodyamica Sinica, 2009, 27(5): 524-528.(in Chinese). doi:10.3969/j.issn.0258-1825.2009.05.004. 王文正, 桂业伟, 何开锋, 等. 基于数学模型的气动力数据融合研究[J]. 空气动力学学报, 2009, 27(5): 524-528. |