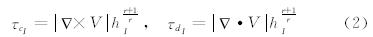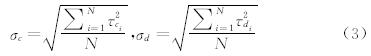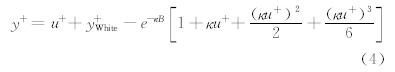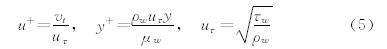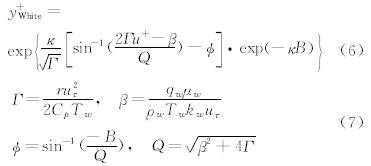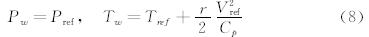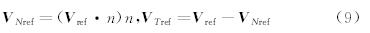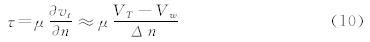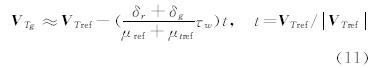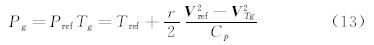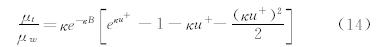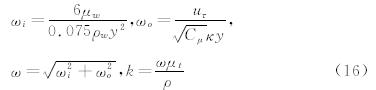2. 中航工业直升机设计研究所, 江西 景德镇 333000
2. AVIC China helicopter research and development institute, Jingdezheng 333000, China
网格生成是采用计算流 体力学(Computational Fluid Dynamics,CFD)进行数值模拟的先行工作,目前较为成熟的网格形式有结构网格、非结构网格和笛卡尔网格。笛卡尔网格是一种区别于前两者的非贴体网格类型。由于早期多采用结构化的直角网格形式,在处理复杂外形时所需要的网格数目巨大,并未得到广泛的应用。随着计算机水平和数值方法的发展,尤其是自适应网格加密(Adaptive Mesh Refinement,AMR)技 术的提出,使得笛卡尔网格在复杂流动问题中凸显出了其独特的优势:1)简化复杂几何外形的网格生成过程,不需要过多的人为技巧和经验;2)易于实现基于几何外形和流场特征的网格自适应技术,能够减少计算网格的数量并且提高流场的分辨率;3)笛卡尔网格系统易于和高精度数值计算方法耦合。
采用纯笛卡尔网格方法进行数值模拟的最大难点在于物面条件的满足。早期的学者们多采用切割单元[1]的方法,即切割与物体表面相交的笛卡尔网格单元,只保留浸没在流场中的部分,使得笛卡尔网格具备了贴体的特性。但是,该方法具有自身的局限性:切割后的单元形式多样,使原有的网格数据类型变得复杂,三维情况时会更加明显;同时切割过程中可能形成微小的网格单元,造成方程系统的刚性问题,影响流场的收敛特性并在物面边界处产生流场解的非物理振荡。为此Udaykumar[2]提出了融合单元处理技术,Munikrishna等人[3]提出了网格缝合处理技术对切割单元方法进行了改进。另一方面,浸入类边界处理方法也引起越来越多的关注,其与切割单元方法相比避免了复杂的几何求交运算以及小网格单元出现所带来的诸多缺点。浸入边界方法(Immersed Boundary Method,IBM)最初在低速不可压流动中广泛应用,成功地数值模拟了流固耦合、大位移运动边界等诸多问题。在可压缩流动方面,Forrer和Jeltsch[4]首次基于笛卡尔网格引入虚拟单元方法处理无粘可压缩流动问题,该方法不考虑物面的存在,把物体作为边界条件嵌入到流场中,而边界条件通过某种重构强加在物体内部的虚拟单元上。随后Dadone等人[5]对虚拟单元方法进行了细致深入的研究,考虑物面曲率的影响引入了曲率修正和熵修正。目前,该类方法的研究热点集中在可压缩粘性流动问题的数值模拟,尤其是面向高雷诺数的湍流流动问题。相对于无粘和层流流动问题,浸入类笛卡尔网格方法应用到湍流流动时面临的难点有:1) 高雷诺数 下如何准确定义湍流壁面边界条件,模拟壁面湍流效应;2) 在不影响流场计算精度及边界层分辨的情况下,如何降低计算网格数量,尤其是物面附近的网格数量,提高计算效率。一些学者基于浸入类笛卡尔网格方法使用十分细密的网格给出了湍流流动的数值模拟结果,与贴体类网格方式相比,壁面附近网格需求量巨大导致了计算量很大,限制了方法在复杂几何外形流动和三维流动问 题中的使用。为此,从减少物面边界附近网格数量的目的出发,使用壁面函数模型来定义湍流边界条件成为一种可行的方式:Kalitzin和Iaccarino[6]提出了一种基于壁面律的浸入边界方法处理高雷诺数湍流问题;Jae-doo Lee[7]基于虚拟单元浸入边界方法,通过耦合壁面函数模型与k-ε湍流模型来定义壁面边界条件;Capizzano[8]Two-layer wall modeling修正浸入边界网格交接面上湍流变量值。
国内有关浸入边界笛卡尔网格方法在高雷诺数可压缩流动问题中的研究和应用还并不多见,作者在前人的工作基础上,基于浸入边界虚拟单元方法,研究了贴体网格下壁面函数模型的作用和实现模式,从壁面函数的基本假设出发构造了一种壁面函数-虚拟单元方法(Wall Function-Ghost Cell Method,WF-GCM)。本文基于自适应笛卡尔网格和有限体积方法,发展了一套可用于求解二维高雷诺数可压缩粘性流动的求解器,耦合SST k-ω湍流模型与WF-GCM,成功定义了高雷诺数下的湍流壁面条件,并依据壁面函数模型修正近壁面单元和界面单元上的湍流变量值和湍流粘性系数。 1 数值方法 1.1 控制方程的求解
积分守恒形式的RANS方程表达式如下:
守恒变量 W ,对流通量 F c和黏性通量 F v的具体形式参见文献[9]。本文采用了基于非结构网 格数据形式的格心格式有限体积方法来求解上式。时间推进采用LU-SGS(Lower-Upper Symmetric Gauss-Seidel)隐式格式[10];空间离散上选取AUSM+(Advection Upstream Splitting Method Plus)[11] 近似Riemann求解器并加入Venkatakrishnan限制器[12]来抑制间断区域的非物理振荡,同时为获得解的二阶精度进行了解的线性重构。湍流模型选取SST k-ω两方程模型[13]。远场边界采用特征边界条件[9];采用虚拟单元方法来定义湍流壁面边界条件,具体内容在第2节给出。 1.2 基于流场特征的网格自适应方法
笛卡尔网格生成过程中,二维采用四叉树(三维八叉数)的数据结构来储存网格信息,叉数状数据结构的最大优势就是能够十分便利地进行网格的加密和粗化,网格自适应技术的产生和发展也直接推动了笛卡尔网格在流动模拟中的应用。本文为了提高流场结构的分辨率基于流场特征进行了解自适应操作。文献[14]对比了不同的解自适应判据,认为结合速度散度和旋度的综合判据是十分有效的,表达式如下:
这里I=1,2,...,N。N代表网格总数。hI=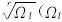 是网格单元的体积,二维时r=2,三维时r=3)。两个参数的标准差定义如下:
计算过程中自适应判断标准如下:
是网格单元的体积,二维时r=2,三维时r=3)。两个参数的标准差定义如下:
计算过程中自适应判断标准如下: 1) 如果网格单元满足τci>σc或者τdi>σd,则网格需要加密;
2) 如果网格单元满足τci<0.3σc或者τdi<0.1σd,则网格需要粗化。 2 壁面函数-虚拟单元方法 2.1 壁面函数模型
壁面函数模型是一种由边界层理论推导得到的经验模型,其建立需要满足六条假设[15]:
1) 边界层底部区域的速度分布和温度分布可以解析的表达;
2) 近壁面第一层网格点上的湍流输运参数可以解析的表达;
3) 边界层底部区域压力分布是常数;
4) 边界层底部区域剪切应力分布是常数;
5) 边界层底部区域热量传递是常数;
6) 边界层底部区域内没有化学反应。
文献[15]依据上述假设考虑流体可压缩性以及物面热传导的影响,修正了Spalding的壁面函数模型[16],给出了一种新的函数模型,定义如下:
式中y+和u+分别代表无量纲的边界层厚度和边界层内的速度,定义如下: 式(4)式(5)中vt为切向速度大小,y为单元中心到壁面的垂直距离,ρw、μw、τw、uτ分别为壁面流体的密度、层流粘性系数、剪切应力和摩擦速度,常数κ和B分别0.41和5.5。修正项y+White表达式如下: 式中Г、β分别表示可压缩性和热传导的影响。r=Pr1/3(Pr=0.72),Cp为空气定压比热容,qw、Tw、kw分别为壁面热流密度、壁面温度和壁面热传导系数。本文考虑的粘性问题都为绝热壁,因此β=0,qw=0。 2.2 虚拟单元方法虚拟单元方法中,笛卡尔网格单元被分为三类:界面单元,固体单元和流体单元。将与界面单元相邻的固体单元定义为虚拟单元(Ghost Cell,GC),将与界面单元相邻的流体单元定义为近壁面单元(Near Wall Cell,NWC)。计算过程中流体单元和界面单元构成计算单元,而固体单单元不参与计算。无粘虚拟单 元方法在文献[17]中已有详细的介绍,其基本思想是在壁面附近通过边界条件的线性重构获得虚拟单元上的虚拟流场信息。但是高雷诺数可压流动问题中附面层结构是非线性的,沿用原有的线性重构会带来如下的两点问题:1) 笛卡尔网格的非贴体性和虚拟单元的对称点的不均匀分布可能引起附面层内流动的非物理振荡。2) 虚拟单元的对称点必须落在附面层中的粘性底层区域,这就要求壁面附近的笛卡尔网格单元尺度很小,因此网格数量会剧烈增加。
粘性计算时,为解决上述两点问题,引入参考点的概念来取代无粘情况下的对称点。同时,基于壁面函数修正湍流壁面边界条件从而改变物面上的通量计算。 2.2.1 参考点与壁面函数相关参数的确定
如图 1所示,点E,G分别为虚拟单元A,F的参考点,参考点的取法以A点为例:首先找到A点距离物面的最近点B,延长AB至E使得BE的长度为物面网格尺度h的 2 倍。与无粘情况时取关于物面的对称点不同,该种取法中所有参考点到物面的距离都一致,从而具有了结构网格的一些特点,同时该种取法保证了插值获得参考点流场基本变量值过程中用到的四个模板点S1、S2、S3、S4都为流体单元。根据壁面函数的基本假设(3)和Crocco-Busemann关系得到壁面上的压力和温度:
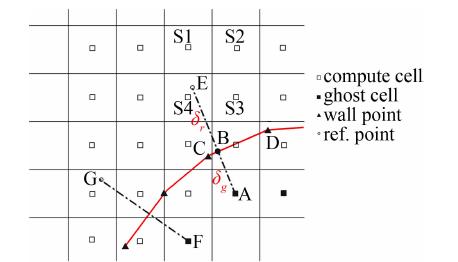 |
| 图 1 虚拟单元方法示意图Fig. 1 Example configuration of the ghost cell method |
壁面函数基本假设式(4)认为壁面附近的剪切应力为常数分布,根据牛顿摩擦阻力公式:
可以得到虚拟单元上的切向速度分量为: 同时虚拟单元上法向速度分量满足无穿透条件: 虚拟单元上压力和温度的计算方法同上节中物面点类似: 密度ρg可由状态方程解出。结合式(4)式(5)将y+对u+求导得到近壁面处湍流粘性系数与层流粘性系数的关系式:
根据虚拟单元和参考点上总粘性系数相等,则可以求得虚拟单元A上的湍流粘性系数为:SST k-ω两方程模型中k和ω可以采用下式得到:
其中常数Cμ和κ分别取值为0.09与0.41。Nichols等人指出,采用壁面函数处理湍流问题时,除了上述提及的边界条件的定义之外,靠近物面的网格单元还需要进行湍流变量值和湍流粘性系数的修正,此处虚拟单元方法中对近壁面单元和界面单元都根据壁面函数模型做出了修正,具体修正方法参见文献[15]。 2.2.3 笛卡尔网格WF-GCM的实施流程
综上所述,可以将基于笛卡尔网格的WF-GCM流程总结如下:
1) 划分单元类型,确定流体单元、固体单元、界面单元,定义虚拟单元和近壁面单元,找到虚拟单元的参考点并确定各点的几何信息;
2) 插值计算参考点的流场信息,得到壁面压力、温度、速度、密度、层流粘性系数,并结合壁面函数模型公式(4)求解壁面剪切应力和摩擦速度;
3) 由式(10)~式(16)计算得到虚拟单元上的基本流场变量和湍流变量;
4) 根据壁面函数模型修正近壁面单元和界面单元上的湍流变量值和湍流粘性系数。 3 数值算例与分析 3.1 平板绝热流动的数值模拟
该算例来源于文献[7],来流马赫数为0.2,基于平板长度的雷诺数为1.0927×107。计算采用了贴体的结构网格,通过疏密不同的四套网格以及开关壁面函数模型验证了壁面函数模型的准确性,并分析了其与网格尺度之间的关系。平板展向布置120个网格,法向分别布置50、60、80、100个网格,对应物面网格的y+分别为1、5、20、40。从图 2给出的平板表面摩擦系数分布可以看出,当y+=40时,关闭壁面函数模型,计算结果和实验值偏差很大,而采用壁面函数模型后,计算结果得到明显的改善;同时可以看出采用壁面函数模型后不同网格尺度下的计算结果基本与实验值相近,对网格的依赖性减小。表 1给出了四套网格下x=0.685处的壁面摩擦系数Cf的数 值。数据结果显示y+=5、20、40时采用壁面函数模 型的计算结果与y+=1时的计算结果以及实验值都比较吻合;而当y+=40不采用壁面函数模型的情况下,Cf的相对误差达到了26.5%。
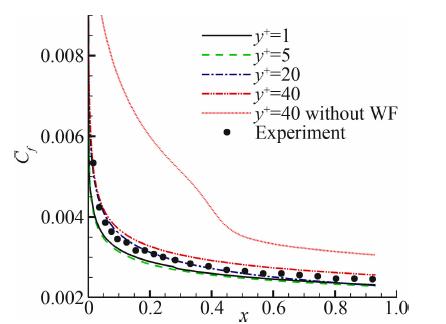 |
| 图 2 不同网格下平板表面的摩擦系数分布Fig. 2 Friction drag coefficient on the surface in different meshes |
Cook等人[18]对RAE2822翼型的绕流问题进行了详细的实验研究,故其常作为测试流场求解器准确 性的标准算例。本文选取的计算状态为:来流马赫数M∞=0.73,攻角α=2.79°,雷诺数Re∞=6.2×106。
该状态下,翼型上表面会产生一道明显的激波,激波与附面层相互作用会使得附面层变厚并同时伴随着激波诱导所产生的轻微流动分离,这些都给准确地数值模拟增加了难度。计算域大小取弦长(c=1.0)的20倍,将计算域划分成80×80的网格单元,初始背景笛卡尔网格步长为Hmax=0.25,依据翼型表面进行了8次几何自适应加密后,最小网格尺度达到Hmin=Hmax/28。计算过程中基于速度旋度和散度判据进行了三次(AMR=3)解自适应加密,网格数量从初始的33054依次增加为81474、178760、379927。图 3给出了初始网格(图 3a)和三次解自适应之后的计算网格(图 3b);图 4给出了AMR=3时计算所得的马赫数云图;图 5将采用WF-GCM得到的翼型表面压力系数Cp分布与贴体网格的计算结果以及实验值进行了比较。从图 5中可以看到,初始计算网格得到的前缘Cp峰值偏低,激波位置偏差较 大,随着解自适应次数的增加,前缘Cp峰值和激波 位置得到了明显的改善,当AMR=3时的计算结果和贴体网格计算所得到的结果十分一致,但是过激波后的Cp分布与实验值都存在一定的误差。表 2给出了该状态下计算所得的升阻力系数与实验值的对比,从结果可以看到,伴随着解自适应的进行升阻力系数得到了明显的改善,在AMR=3时升力系数的误差小于2%,阻力系数的误差小于7%。
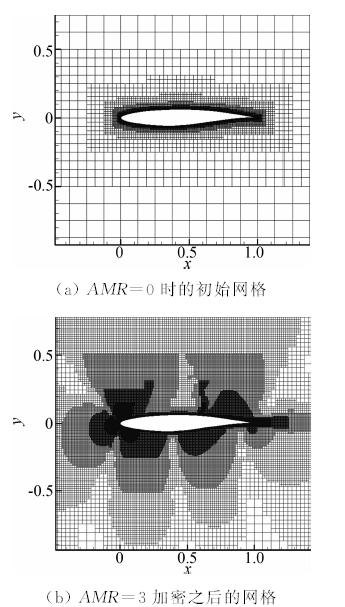 |
| 图 3 初始网格与解自适应加密网格(AMR=3)Fig. 3 Initial mesh and feature-adapted mesh(AMR=3) |
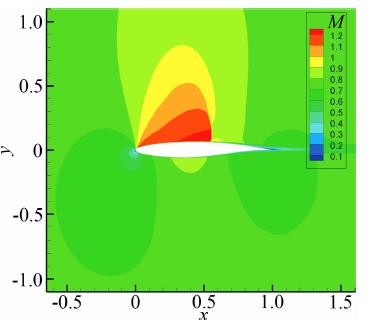 |
| 图 4 马赫数云图的计算结果(AMR=3) Fig. 4 Computed result of Mach contours(AMR=3) |
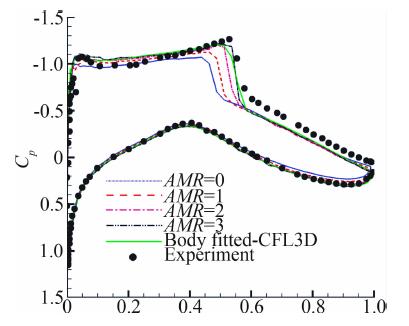 |
| 图 5 压力系数分布的比对Fig. 5 Comparison of Cp distribution |
该算例考察WF-GCM在处理超声速流动问题时的有效性和准确性。取来流马赫数为1.7,基于圆柱直径的雷诺数为2×105,在该状态下,圆柱上游会形成一道弓形激波,过激波后流动加速会在圆柱后缘再次形成两道激波,同时伴随着圆柱后缘的流动分离,上述复杂的流动现象都增加了采用WF-GCM进行数值模拟难度。计算区域大小取为[-8D,9D]×[-8D,8D],其中D为圆柱直径。计算过程中基于速度旋度和散度判据进行了三次(AMR=3)解自适应加密,最终网格总数目达到184684,图 6给出了最终的计算网格(图 6a)与马赫数云图(图 6b)。图 7给出了圆柱尾缘流动分离区域的流线图(图 7a)和对应位置的自适应计算网格(图 7b),可以看出WF-GCM能够捕捉圆柱流动分离现象。图 8将WF-GCM计算所得的圆柱表面Cp分布与实验值[19]进行了对比,从表 3给出的数据可以看到,相对于文献[20]中Munikrishna采用混合网格方法计算所得分离点的位置与阻力系数,WF-GCM计算所得的分离点位置与阻力系数与实验值都更为符合。
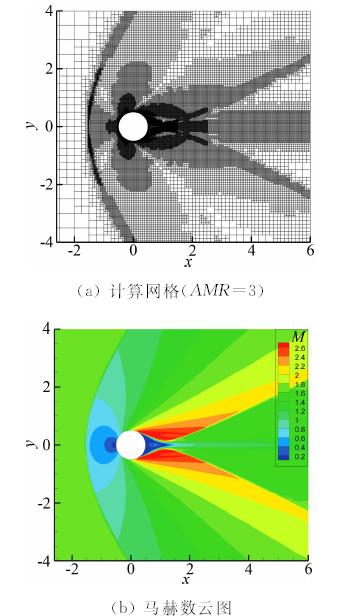 |
| 图 6 超声速圆柱绕流的计算结果Fig. 6 Results of supersonic flow past cylinder |
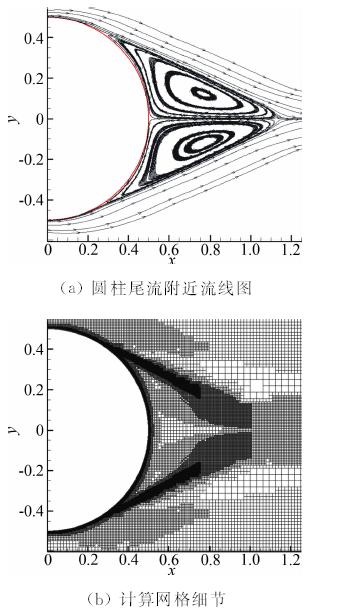 |
| 图 7 圆柱尾流附近流线图及网格细节Fig. 7 Streamlines and mesh in wake flow near cylinder |
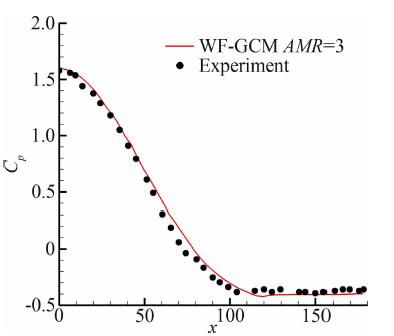 |
| 图 8 压力系数分布的比对Fig. 8 Comparison of Cp distribution |
针对高雷诺数可压缩粘性流动,从几何角度与边界重构数值方法两个方面出发,基于笛卡尔网格虚拟单元方法耦合壁面函数模型,提出了一种全新的湍流壁面边界条件定义方法,用于定义虚拟单元上的虚拟流场信息,并给出了壁面函数模型在非贴体笛卡尔网格中的具体实现模式,在此基础上结合有限体积方法结合发展了可用于高雷诺数可压缩流动问题的壁面函数-虚拟单元方法(WF-GCM)。
本文以贴体网格下平板绝热流动为例,验证了壁面函数模型的有效性与正确性,进而使用WF-GCM数值模拟了跨声速RAE2822翼型绕流与超声速圆柱绕流,通过上述算例的研究可以得到如下结论:
1) 壁面函数模型的使用能够在确保数值模拟准确性的前提下减少网格数量;
2) WF-GCM能够有效准确地数值模拟高雷诺数可压缩粘性绕流,耦合自适应网格加密技术能够提高流场模拟的分辨率与气动力参数计算的准确性;
3) 尽管壁面函数模型不能严格证明在流动分离时依然有效,但从数值结果来看,WF-GCM处理湍流壁面边界条件能够较为准确地捕捉流动分离现象。
| [1] | COIRIER W J, POWELL K G. Solution-adaptive Cartesian cell approach for viscous and inviscid flows. AIAA Journal, 1996, 34(5): 938-945. |
| [2] | UDAYKUMAR H S, UDAYKUMAR H S, KAN H C, et al. Multiphase dynamics in arbitrary geometries on fixed cartesian grids. Journal of Computational Physics, 1997, 137(2): 366-405. |
| [3] | MUNIKRISHNA N, MONDAL P, BALAKRISHNAN N. Cartesian-like grids using a novel grid-stitching algorithm for viscous flow computations. Journal of Aircraft, 2007, 44(5):1598-1609. |
| [4] | FORRER H, JELTSCH R. A higher order boundary treatment for Cartesian-grid method. J. Comput. Phys., 1998, 140: 259-277. |
| [5] | DADONE A, GROSSMAN B. Ghost-cell method for inviscid two-dimensional flows on cartesian grids. AIAA Journal, 2004, 42(12): 2499-2507. |
| [6] | KALITZIN G, IACCARINO G. Toward immersed boundary simulation of high Reynolds number flows. In: Annual Research Briefs 2003. Center for Turbulence Research, Stanford University, 2003. |
| [7] | JAE-Too L. Development of an efficient viscous approach in a cartesian grid framework and application to rotor-fuselage interaction. Georgia: Georgia Institute of Technology, 2006. |
| [8] | CAPIZZANO F. A turbulent wall model for immersed boundary methods. AIAA paper 2010-712, 2010. |
| [9] | BLAZEK J. Computational fluid dynamics: principles and applications. Amesterdam: ELSEVIER,2011. |
| [10] | SHAROV D, NAKAHASHI K. Reordering of 3-D hybrid unstructured grids for vectorized LU-SGS Navier-Stokes calculations . AIAA Paper 97-2102, 1997. |
| [11] | LIOU M S. A sequel to AUSM: AUSM+. Journal of Computational Physics, 1996, 129 (2):364-382. |
| [12] | VENKATAKRISHNAN V. On the accuracy of limiters and convergence to Steady State Solutions . AIAA Paper 93-0880, 1993. |
| [13] | MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications . AIAA Journal, 1994, 32(8): 1598-1605. |
| [14] | ZEEUW D L. A quadtree-based adaptively-refined cartesian-grid algorithm for solution of the Euler equations. Michigan: University of Michigan, 1993. |
| [15] | NICHOLS R H, NELSON C C. Wall function boundary conditions including heat transfer and compressibility for transport turbulence models. AIAA Paper 2004-582, 2004. |
| [16] | SPALDING D B. A single formula for the law of the wall. J. App. Mech., 1961, 28(3): 455-458. |
| [17] | 胡偶, 赵宁, 刘剑明, 等. 基于有限体积格式的自适应笛卡尔网格虚拟单元方法及其应用. 空气动力学学报, 2011, 29(4):491-495. |
| [18] | COOK P H, MCDONALD M A, FIRMIN M C. Aerofoil RAE 2822 - pressure distributions, and boundary layer and wake measurements. In: Experimental Data Base for Computer Program Assessment. AGARD AR 138, 1979. |
| [19] | BASHKIN V A, VAGANOV A V, EGOROV I V, et al. Comparison of calculated and experimental data on supersonic flow past a circular cylinder. Fluid Dynamic, 2002, 37(3):473-483. |
| [20] | MUNIKRISHNA N, LIOU M S. A Cartesian based body-fitted adaptive grid method for compressible viscous flows. AIAA Paper 2009-1500, 2009. |