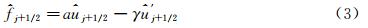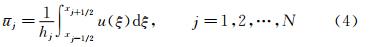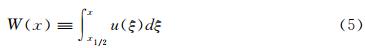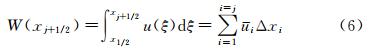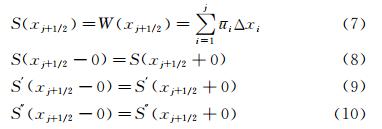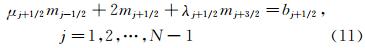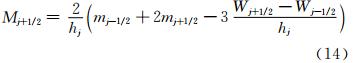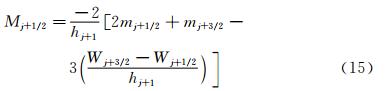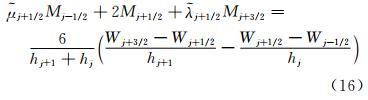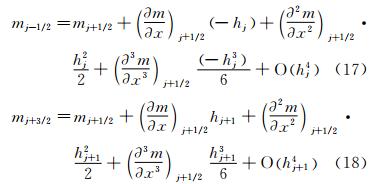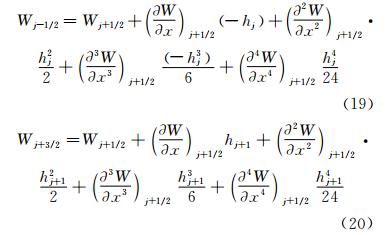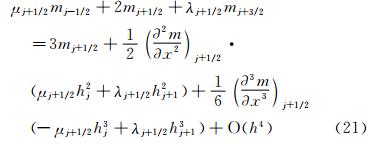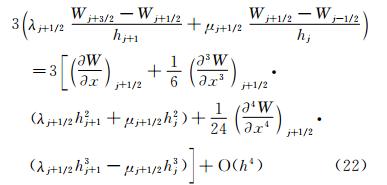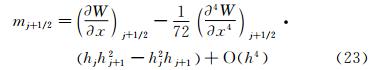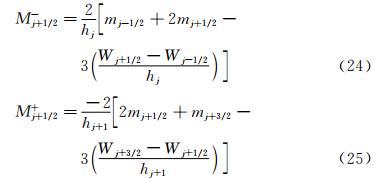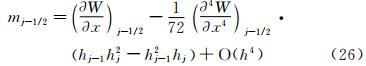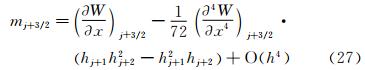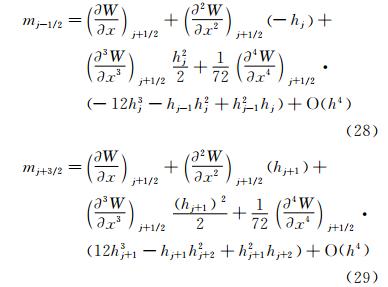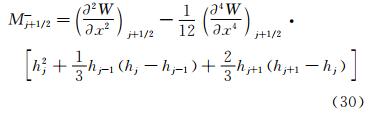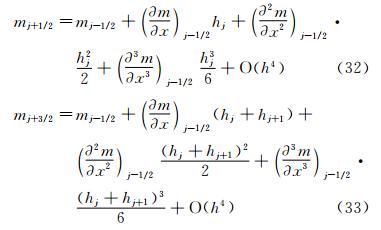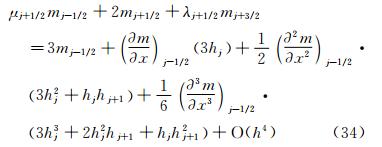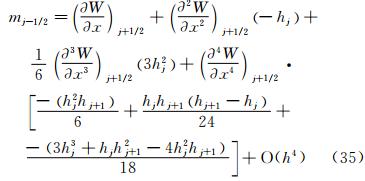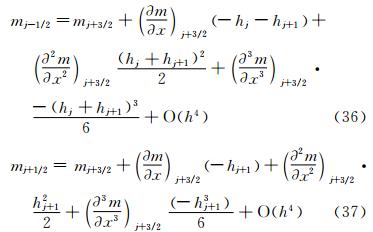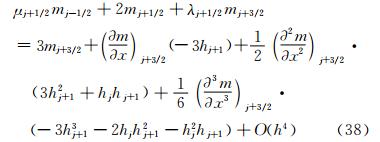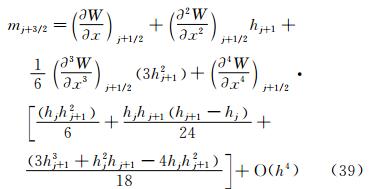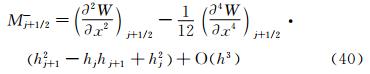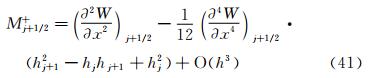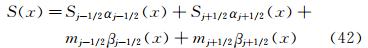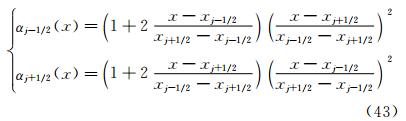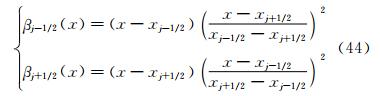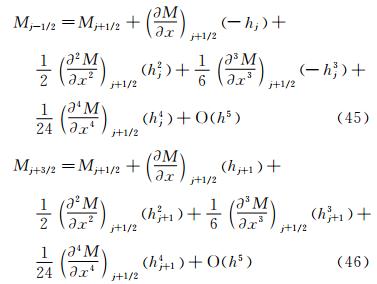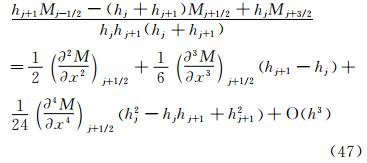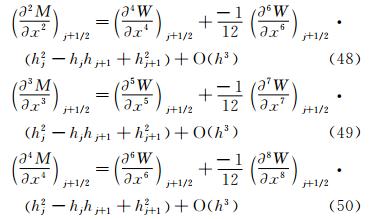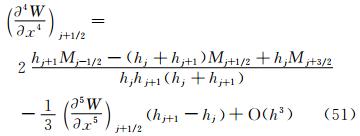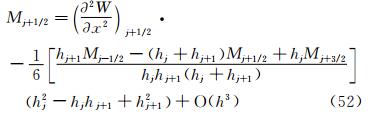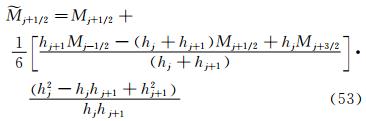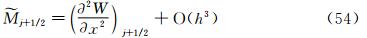样条插值方法是Schoenberg[1]在20世纪40年代提出的。三次样条插值函数具有非常良好的特性,可用于求解偏微分方程[2, 3]。Rubin[4]总结了样条函数在数值求解偏微分方程方面所具有的优点,包括只需求解三对角方程,计算效率高;对函数值、一阶导数和二阶导数都具有良好的逼近效果;边界条件处理非常方便等。许多学者将样条插值方法应用到非线性双曲守恒方程的求解,如,McCartin 和Jameson[5]引入指数样条来处理非光滑的数值解,并采用文献[6, 7, 8, 9]提出的方法计算张力因子;王建立等[10]研究了基于样条逼近有限体积法的通量分裂算法。
紧致格式具有较好的谱特性能分辨流场中的小尺度结构[11];Hermite插值方法在非均匀网格上容易达到高阶精度[12, 13, 14, 15]。样条插值可以看做基于Hermite插值的某种紧致格式。因此,基于样条插值的算法有望在非均匀网格上实现高精度、高分辨率。三次样条插值方法可以直接应用于非均匀网格,无需将非均匀网格通过坐标变换至均匀网格的计算空间。在非均匀网格上,三次样条插值对对流-扩散方程的对流项和扩散项的离散可分别达到三阶精度和二阶精度。在发展求解任意曲线坐标非均匀网格可压缩 流动的高精度样条逼近有限体积方法[16]的过程中 发现,三次样条插值的截断误差具有局部特性,不恰当的推导有可能导致错误结果。因此,提出了在非均匀网格上,分析截断误差的基本准则,即不显式或者隐含地改变数值方法对应的模板点。如果不满足这一准则,将得到不自洽的截断误差分析结果。在满足这一准则的前提下,得出了非均匀网格上用三次样条重构扩散项所产生的截断误差,并利用该截断误差分析结果,发展了扩散项三阶精度离散的计算方法。从而使三次样条重构在非均匀网格上对对流项和扩散项的离散达到一致三阶精度。本文的精度分析所遇到的问题及其解决方案,在非均匀网格高精度数值方法的构造中,具有普遍性,因此对此进行研究是有意义的。
本文将在第2节中给出三次样条重构有限体积方法离散对流扩散方程的具体过程;在第3节中,首先比较截断误差的两种分析方法,通过具体推导过程分析对比得出非均匀网格上分析截断误差的基本准则;在第4节中,将利用截断误差分析,给出扩散项三阶精度的离散方法。本文第5节将给出结论。 1 三次样条重构方法
采用一维标量线性对流扩散方程来说明有限体积框架下样条重构的构造方法,方程为:
其中,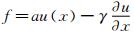 ,
a是波速,γ是扩散系数(均为常数)。在hj=xj+1/2-xj-1/2的计算网格上,式(1)在控制体[xj-1/2,xj+1/2]内的积分形式为:
其中,uj是单元平均值,数值通量为:
其中
,
a是波速,γ是扩散系数(均为常数)。在hj=xj+1/2-xj-1/2的计算网格上,式(1)在控制体[xj-1/2,xj+1/2]内的积分形式为:
其中,uj是单元平均值,数值通量为:
其中 j+1/2和
j+1/2和 ′j+1/2分别是因变量及其一阶导数在控制体界面的近似值,通常由某种重构方法得到。
′j+1/2分别是因变量及其一阶导数在控制体界面的近似值,通常由某种重构方法得到。 本文的有限体积重构方法,采用基于原函数的三次样条重构。已知某时刻u(x)的平均值,定义
u(x)的原函数定义为: 单元界面xj+1/2处的原函数的值为: 因此单元界面处原函数的值可以根据单元平均值计算,三次样条函数S(x)来插值原函数W(x),插值条件为: 对于三次样条多项式,有4N (N为网格节点数)个待定系数,根据式(8)~式(10)有3(N-1)个关系式,再加上式(7)的插值条件,共有4N-2个关系,因此另外需要两个条件就可以确定待定系数。通常在求解域的两个端点 x1/2,xN-1/2 上各加一个边界条件,边界条件根据实际问题确定。在实际实施中,有两种等价的方法可以进行三次样条重构。第一种是求解所谓“三转角”方程,即:
其中,N是网格节点数,并且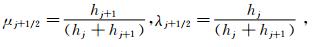
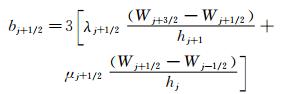
第二种方法求解“三弯矩”方程,即:
其中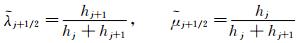 。
。 Mj+1/2是因变量一阶导数的近似,即式(13)。因变量本身在控制体界面处的值可用式(12)计算,其中:
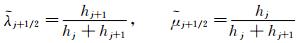
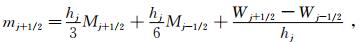 把式(12)、式(13)代入式(3)即可得到数值通量。这种方法可以推广到求解Euler和Navier-Stokes方程;也可以应用于多维曲线坐标非均匀网格的情况。关于格式在上述情况的具体形式,以及稳定性、激波捕捉等问题的分析和处理,请参见文献[16]。本文主要研究在非均匀网格下误差分析的问题。
2 误差分析方法
把式(12)、式(13)代入式(3)即可得到数值通量。这种方法可以推广到求解Euler和Navier-Stokes方程;也可以应用于多维曲线坐标非均匀网格的情况。关于格式在上述情况的具体形式,以及稳定性、激波捕捉等问题的分析和处理,请参见文献[16]。本文主要研究在非均匀网格下误差分析的问题。
2 误差分析方法
根据第2节,在进行重构时,我们既可以通过求解三转角方程计算 j+1/2,也可以根据三弯矩方程计算
j+1/2,也可以根据三弯矩方程计算 ′j+1/2。这两种方法在边界条件相容时,是完全等价的。所以,下面只分析求解三转角方程的情形。首先研究m的精度。将式(11)等式两边在j+1/2处进行泰勒级数展开。式(11)等式左边mj-1/2,mj+3/2的泰勒级数展开式分别为:
′j+1/2。这两种方法在边界条件相容时,是完全等价的。所以,下面只分析求解三转角方程的情形。首先研究m的精度。将式(11)等式两边在j+1/2处进行泰勒级数展开。式(11)等式左边mj-1/2,mj+3/2的泰勒级数展开式分别为:
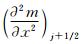 和
和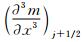 项,得到
在求解三转角方程的条件下,二阶导数M可根据式
(14)或式(15)计算。为了便于区分,式(14)及式(15)分别写为:
项,得到
在求解三转角方程的条件下,二阶导数M可根据式
(14)或式(15)计算。为了便于区分,式(14)及式(15)分别写为:
从数值上,上述两个公式得到的计算结果完全相同,因此,这两种方法的误差也应该是相同的。根据式(24)和式(25)对M的误差分析有两种方法,下面将给出这两种方法,并对其分析过程进行对比。 2.1 分析方法1
根据式(23)一阶导数mj+1/2的表达式,可推知mj-1/2和mj+3/2的表达式分别为:
和 把上面两个公式分别在j+1/2处做泰勒级数展开: 同时,原函数Wj-1/2和Wj+3/2在j+1/2处的泰勒级数展开式为式(19)~式(20)。将式(23)、式(28)~式(29)和(19)~式(20)代入到式(24)、式(25),有 对比式(30)、式(31)中的Mj+1/2-和Mj+1/2+可以发现,二者余项量级是一样的,但系数并不相等。 显然,这种推导方法存在问题,因为Mj+1/2-和Mj+1/2+在数值上是恒等的,因此也应该有完全相同的余项。 2.2 分析方法2将式(11)左侧在j+1/2处做泰 勒级数展开,可得式(23)。同理,我们也可以把式(11)左侧在j-1/2 和j+3/2处展开。当式(11)左侧在j-1/2处展开时,等式左边mj+1/2、mj+3/2的泰勒级数展开式分别为:
式(11)右边,Wj-1/2和Wj+3/2在j+1/2处泰勒级数展开式为式(19)~式(20)。将式(19)~式(20)和式(32)~式(33)代入到式(11)中,则得到等式左边为:
等式右边为式(22)。采用循环消去法,消去式(34)中的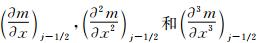 ,得到:
,得到:
同理,将式(11)等式左边在j+3/2处进行泰勒级数展开,等式右边在j+1/2处进行泰勒级数展开。式(11)等式左边mj-1/2,mj+1/2的泰勒级数展开式分别为:
式(11)右边,Wj-1/2和Wj+3/2在j+1/2处泰勒级数展开式为式(19)~式(20)。将式(19)~式(20)和式(36)~式(37)代入到式(11)中,则得到等式左边为:
等式右边为式(22)。采用循环消去法,消去式(38)中的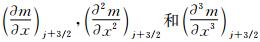 ,得到:
,得到:
将式(19)、式(23)和式(35)代入到式(24),有:
将式(20),式(23)和式(39)代入到式(25),则有:
对比式(40)、式(41)中的Mj+1/2-和Mj+1/2+可以发现,二者余项完全相等。这个结果与Mj+1/2-和Mj+1/2+在数值上恒等是自洽的,因而是正确的。 2.3 两种方法的比较分析
方法1和方法2的不同之处在于:方法1中mj-1/2和mj+3/2在j+1/2处的泰勒级数展开式是在mj+1/2(式(23))的基础上分别向左和向右移动一个单元指标。方法2中mj-1/2和mj+3/2在j+1/2处的泰勒级数展开式是在m关系式(式(11))的基础上,通过循环消去法得到。
为什么方法1不正确而方法2正确呢?这是因为,非均匀网格上的数值方法与均匀网格数值方法不同,其误差估计具有局部特性。例如,式(40)或者式(41)表明Mj+1/2的大小与局部空间步长hj、hj+1有关。如果改变了模板点,则会引入其他模板的长度尺度;而又由于非均匀网格不同单元(或者控制体)的尺度互不相关,因而采用不同模板,会得到不同的结果;从而造成分析的不自洽。因此,我们可以得到非均匀网格误差分析的一个重要原则,即在非均匀网格的误差分析中,只有保证不显式或者隐含地改变数值方法对应的模板点,才能得到正确结果。
为了进一步说明这个问题,下面回顾一下三次样条重构中三转角方程的推导。我们知道在控制体Ij=[xj-1/2,xj+1/2]上,三次样条函数S(x)可以表示为
其中,αj±1/2(x)和βj±1/2(x)是三次Hermite插值基函数,分别为: 和根据式(42),可得式(24);同理根据Ij+1=[xj+1/2,xj+3/2]上的三次样条函数S(x)的表达式,可得式(25)。样条函数要求Mj+1/2-=Mj+1/2+,由式(24)、式(25)即可得到三转角方程式(11)。由此可知,式(11)的模板为单元Ij,Ij+1,因此在进行精度分析时,不能采用在这两个单元以外定义的关系。
方法1在推导过程中,使用了式(23)、式(26)和式(27),且式(26)和式(27)由式(23)平移得到。由于式(23)的模板为单元Ij,Ij+1,则式(26)和式(27)对应的模板分别为Ij-1,Ij和Ij+1,Ij+2。也就是说,在推导出式(30)和式(31)的过程中,二者的模板是不同的,因而余项的结果也不同。在方法2中,所有的推导基于式(11),保证了模板为单元Ij,Ij+1。这与三转角方程的推导相一致,从而可以得到正确的结果。另外,我们注意到,在均匀网格上,两种方法得到的结果是相同的。 3 扩散项的三阶精度离散方法
通过精度分析可知,样条重构得到的界面因变量 j+1/2=mj+1/2在均匀网格上,逼近精确解到4阶精度;在非均匀网格上,逼近精确解到3阶精度。对于扩散项的重构,
j+1/2=mj+1/2在均匀网格上,逼近精确解到4阶精度;在非均匀网格上,逼近精确解到3阶精度。对于扩散项的重构, ′j+1/2=Mj+1/2在均匀或者非均匀网格上,都可以逼近精确解到二阶精度。事实上,利用M的误差分析,有可能设计三阶精度的
′j+1/2=Mj+1/2在均匀或者非均匀网格上,都可以逼近精确解到二阶精度。事实上,利用M的误差分析,有可能设计三阶精度的 ′j+1/2=Mj+1/2的重构方案。其基本思路是对二阶导数误差中(式(40)或者式(41))的
′j+1/2=Mj+1/2的重构方案。其基本思路是对二阶导数误差中(式(40)或者式(41))的 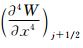 项做一阶精度近似,具体方法如下。
项做一阶精度近似,具体方法如下。
首先,计算Mj-1/2和Mj+3/2在j+1/2处的泰勒级数展开式,
根据式(45)和式(46)可以计算得到:
为消去式(47)中的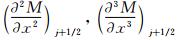 和
和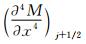 ,需要根据式(40)给出
,需要根据式(40)给出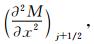
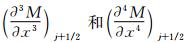 的表达式,分别为:
的表达式,分别为:
将式(48)~式(50)代入到式(47)中,得到:
将式(51)代入到式(40)得到:
令: 则有: 因此得到二阶导数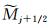 逼近
逼近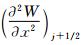 到三阶精度,即
到三阶精度,即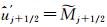 逼近
逼近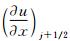 至三阶精度。因此,
至三阶精度。因此,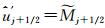 的重构方案对方程扩散项的离散在均匀或者非均匀网格上,都可以逼近精确解至三阶精度。
4 结 论
的重构方案对方程扩散项的离散在均匀或者非均匀网格上,都可以逼近精确解至三阶精度。
4 结 论
本文研究了有限体积方法框架下,在非均匀网格上采用三次样条重构方法离散方程对流项和扩散项所产生的截断误差的分析方法。通过具体推导过程的比较分析,提出了非均匀网格上截断误差分析的基本准则,即保证不显式或隐含地改变数值方法对应的模板点。若不满足该准则,将得到不自洽的误差分析结果。本文在该准则的基础上得出了对扩散项离散的截断误差,提出了提高扩散项离散精度的方法,发展了在非均匀网格上扩散项三阶精度离散的计算方法。从而使三次样条重构在非均匀网格上对方程对流项和扩散项的离散达到一致三阶精度。
| [1] | SCHOENBERG I J. Cardinal spline interpolation. In: CBMS-NSF region conference series in applied mathematics 12. Philadelphia, PA: Society for industrial and applied mathematics, 1973. |
| [2] | AHLBERG J, NILSON E, WALSH J. The theory of splines and their applications, academic press. New York: 1967. |
| [3] | RUBIN S G, GRAVES R A. Cubic spline approximation for problems in fluid mechanics. NASA TR R-436, 1975. |
| [4] | RUBIN S G, KHOSLA P K. Higher-order numerical solutions using cubic splines. AIAA Journal, 1976, 14(7): |
| [5] | MCCARTIN B J, JAMESON A. Numerical solution of nonlinear hyperbolic conservation laws using exponential splines. Computational Mechanics, 1990, 6; 77-91. |
| [6] | MCCARTIN B J. Theory, computation, and application of exponential splines. DOE/ER/03077-171(1981). |
| [7] | MCCARTIN B J. Applications of exponential splines in computational fluid dynamics. AIAA J., 1983, 21: 1059-1065. |
| [8] | MCCARTIN B J. Theory of exponential splines. J. Approx. Theory, 1991, 66(1): 1-23. |
| [9] | MCCARTIN B J. Computation of exponential splines. SIAM J. Sci. Stat. Comp., 1990, 11(2): 242-262. |
| [10] | 王建立, 任玉新, 沈孟育. 基于样条逼近有限体积法的通量分裂算法. 计算物理, 2000, 17(4): 421-425. |
| [11] | LELE S K. Compact finite-difference schemes with spectral-like resolution. Journal of Computational Physics, 1992, 103(1): 16-42. |
| [12] | ZHONG X, TATINENI M. High-order non-uniform grid schemes for numerical simulation of hypersonic boundary-layer stability and transition. J. Comput. Phys., 2003, 190: 419-458. |
| [13] | MAHESH K. A family of high order finite difference schemes with good spectral resolution. J. Comput. Phys., 1998, 145: 332-358. |
| [14] | CHU P C, FAN C. A three-point combined compact difference scheme. J. Comput. Phys., 1998, 140: 370. |
| [15] | CHU P C, FAN C. A three-point sixth-order nonuniform combined compact difference . J. Comput. Phys., 1999, 148: 663. |
| [16] | WANG Q J, REN Y X, An accurate and robust finite volume scheme based on the spline interpolation for solving the Euler and Navier-Stokes equations on non-uniform curvilinear grids. Journal of Computational Physics, (submitted). |