2. 河海大学, 江苏南京 210098
2. Hehai University, Nanjing 210098, China
流动稳定性问题中, 小扰动波的传播速度是一个重要的问题。尤其是三维问题, 例如在三维边界层转捩问题中, 一个局部扰动的传播途径, 决定了下游转捩发生的位置。
对于保守系统, 例如水波问题, 色散关系中的波数α和频率ω都是实数, 扰动波的传播速度是群速度, 而且也等于能流的速度[1]。但对于非保守系统, 情况就不同了, 这时α、ω一般不能同时都为实数, dω/dα一般也不是实数。因而, 波的传播速度是什么, 是否还等于能流速度, 都没有明确的答案。
在流动稳定性的研究中涉及的都是非保守系统。因此, 为了能正确地预报扰动波向下游传播的情况, 特别是能预报三维波向下游传播的途径, 就有必要研究非保守系统中, 波的传播速度, 并澄清波的能流速度与波的传播速度之间的关系。这是一个十分重要的理论问题。
M. Gaster[2]曾通过研究二维局部扰动传播问题对这一问题进行了研究。他将局部扰动表述为如下的积分:
| $ \int_{ - \infty }^\infty A (\alpha ){e^{i(\alpha x - \omega t)}}{\rm{d}}\alpha $ |
然后用最速下降法研究了x/t取给定值, 当t充分大时, 该积分的渐近表达式。所得结论为, 所观察到的波的波数和频率α*, ω*, 应使得(dω/dα) |α*=x/t, 这时α*, ω*均可为复数, 而x/t为实数, 因此(dω/dα) |α*也应为实数。但对于一个实际问题, 这一条件往往无法满足。例如, 在转捩实验中, 通过人工方法引入扰动的空间模式里, ω一定是实数, 而α及dω/dα则一般不是实数。在平面槽道流和平板边界层流中, 给定ω或α的实部时, 由特征关系式, 甚至有时找不到能使dω/dα为实数的参数。因此, Gaster的工作并未完全解决这一问题。
Cabeci & Stawartson[3]在研究三维边界层转捩问题中, 在给定α或β时, 曾用dα/dβ为实数的条件来确定另一参数, 以便得到局部扰动的传播方向。这里α是流向波数, β是横向波数。而在求dα/dβ时, 波的频率ω为给定实数, 且雷诺数也给定。这一条件的推导与Gaster一样, 是用最速下降法求渐近表达式而得到的。但这一定义同样有有时无法实现的问题。例如, Radeztsky, Reibert & Saric[4]所做的后掠翼横流涡演化实验中, ω及β都是给定的实数。这时dα/dβ一般就不是实数。
吴岩曾就水槽中的造波实验做过数值模拟。通过在一端造波, 经一段的时间后计算规则波的传播距离来求波的传播速度, 结果又一次证实了水波的传播速度是群速度dω/dα (私人通讯)。有鉴于此, 本文将用数值模拟的办法, 在平面槽道流的某一剖面处引入给定频率的Tollmien-Schlichting波(T-S波), 模拟实验中T-S波的空间演化。在一定时间后通过量得规则波的前进距离来研究波的传播速度。
1 计算模型与数值方法考虑平面槽道流, 设平板法向为y, 波的传播方向为x, 用平均流的最大速度U0与半槽宽度h对N-S方程及连续方程无量纲化, 可得
| $ \frac{{\partial u}}{{\partial t}} + (u \cdot \nabla )u = - \nabla P + \frac{1}{R}{\nabla ^2}u $ | (1, a) |
| $ \nabla \cdot u = 0 $ | (1, b) |
其中u= (u, v, w)为流体的速度, P为压力, 雷诺数R=U0h/γ, γ为运动粘性系数, ∇为梯度算子, ∇2=∇·∇, 在y=±1处, 边界条件为u=0。
在流动稳定性的线性理论中, 设速度、压力的扰动部分有行进波形式的解, 即设
| $ \begin{array}{*{20}{l}} {u = \bar u + \mathit{\boldsymbol{\hat u}} = \bar u + \left( {\tilde u(y){e^{i(ax + \beta z - \omega t)}} + 共轭项} \right)}\\ {P = \bar P + \hat p = \bar P + \left( {\tilde p(y){e^{i(\alpha x + \beta z - \omega t)}} + 共轭项} \right)} \end{array} $ | (2) |
其中, u= (u, 0, w), P为平均流速及压力, 满足定常的N-S方程,
| $ \begin{array}{l} - i\omega \tilde u + (i\alpha \bar u + i\beta\bar w)\tilde u + \bar u'\tilde v = - i\alpha \tilde p + \frac{1}{R}\left( {{D^2} - {\alpha ^2} - {\beta ^2}} \right)\tilde u\\ - i\omega \tilde v + (i\alpha \bar u + i\beta \bar w)\tilde v = - D\tilde p + \frac{1}{R}\left( {{D^2} - {\alpha ^2} - {\beta ^2}} \right)\tilde v\\ - i\omega \tilde w + (i\alpha \bar u + i\beta \bar w)\tilde w + \bar w'\tilde v = - i\beta \tilde p + \frac{1}{R}\left( {{D^2} - {\alpha ^2} - {\beta ^2}} \right)\tilde w\\ i\alpha \tilde u + i\beta \tilde w + D\tilde v = 0 \end{array} $ | (3) |
其中D≡d/dy。由(3)式消去
| $ \left. {\frac{1}{R}{{\left( {{D^2} - {\alpha ^2} - {\beta ^2}} \right)}^2} - i(\alpha \bar u + \beta \bar w - \omega )\left( {{D^2} - {\alpha ^2} - {\beta^2}} \right) + i\alpha {{\bar u}^{\prime \prime }} + i\beta{{\bar w}^{\prime \prime }}} \right]\tilde v = 0 $ | (4) |
在y=±1处的边界条件为
方程(4)与边界条件构成一特征值问题, 可得关于ω、α、β、R的特征关系式。对于给定的R、ω、β, 可以求出特征值α和特征函数
| $ {\mathit{ \Phi } _0} = \int\limits_{ - 1}^1 {\left[ {\left( {\tilde u{{\tilde p}^*} + {{\tilde u}^*}\tilde p} \right) + \bar u\left( {\tilde u{{\tilde u}^*} + \tilde v{{\tilde v}^*} + \tilde w{{\tilde w}^*}} \right)} \right]{\rm{d}}y} $ |
x方向上单位长度中波的能量为:
由此可得波的能流速度为: Ue=Φ0/Φ1
其中上标星号表示共轭项。另一方面, dω/dα可以通过数值计算的方法由特征关系求出。
数值模拟时, 考虑扰动的线性方程。设速度, 压力可分解为
| $ \frac{{\partial \mathit{\boldsymbol{\hat u}}}}{{\partial t}} + (\mathit{\boldsymbol{\bar u}} \cdot \nabla )\mathit{\boldsymbol{\hat u}} + (\mathit{\boldsymbol{\hat u}} \cdot \nabla )\mathit{\boldsymbol{\bar u}} = - \nabla \hat p + \frac{1}{R}{\nabla ^2}\mathit{\boldsymbol{\hat u}} $ | (5,a) |
| $ \nabla \cdot \mathit{\boldsymbol{\hat u}} = 0 $ | (5,b) |
边界条件是y=±1时,
积分(5)式时用时间分裂法。时间导数采用显—隐分裂格式[5]
| $ \frac{{\mathit{\boldsymbol{u'}} - \sum\limits_{q = 0}^2 {{\alpha _q}} {{\mathit{\boldsymbol{\hat u}}}^{\mathit{\boldsymbol{n}} - \mathit{\boldsymbol{q}}}}}}{{\Delta t}} = - \sum\limits_{q = 0}^2 {{\beta_q}} \left( {{{\mathit{\boldsymbol{\bar u}}}^{n - q}} \cdot \nabla {{\mathit{\boldsymbol{\hat u}}}^{n - q}} + {{\mathit{\boldsymbol{\hat u}}}^{n - q}} \cdot \nabla {{\mathit{\boldsymbol{\bar u}}}^{n - q}}} \right) $ | (6) |
| $ \frac{{\mathit{\boldsymbol{u''}} - \mathit{\boldsymbol{u'}}}}{{\Delta t}} = - \nabla {\hat p^{n + 1}} $ | (7) |
| $ \frac{{{\gamma _0}{{\mathit{\boldsymbol{\hat u}}}^{n + 1}} - \mathit{\boldsymbol{u''}}}}{{\Delta t}} = \frac{1}{R}{\nabla ^2}{\mathit{\boldsymbol{\hat u}}^{n + 1}} $ | (8) |
其中u′, u″为中间速度场, 要求u″满足连续性方程。由(7)可得压力满足的方程
| $ {\nabla ^2}{\hat p^{n + 1}} = - \nabla \cdot u'/\Delta t $ | (9) |
上式中取γ0=11/6, α0=3, α1=3/2, α2=1/3, β0=3, β1=-3, β2=1。(6)式中非线性项的空间导数采用五阶迎风紧致格式, (7)式、(9)式中求梯度、散度时采用六阶对称紧致格式, (8)式、(9)式中拉普拉斯算子采用九点隐式四阶紧致格式[6]。(8)式中由于雷诺数较大, 求解拉普拉斯算子采用方向交替法, 方程(9)中用高斯消去法直接求解。在计算三维扰动时, z方向用傅里叶级数展开。
计算时的物理模型为在无扰动的流场入口处传入一个定常幅值的T-S波, 考察该波沿x方向传播的速度。对于二维波, x方向与流向一致, 在x向上取一个有限区域, 0≤x≤xn。在x=0处引入已知扰动, 即x=0的边界条件为
输入的二维波分四种不同情况: (1)与中性曲线端点临界雷诺数对应的中性波, (2)雷诺数取为临界雷诺数但衰减率较大的波, (3)一般的不稳定波, (4)一般的衰减波。
图 1给出了扰动波向下游传播的数值模拟结果, 给出的是y=0.84处扰动速度u沿x方向的分布。数值模拟得到的波的传播速度Ub的确定方法为, 计算到一定时刻t时, 确定波的规则部分端部的位置x, 如图 1中所示的·点, (虽然不能绝对准确地确定这一位置的地方, 但还是可以有一个大体确定的值)。这样波的传播速度Ub就等于x/t。
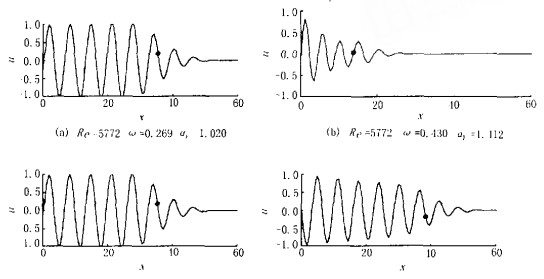
|
图 1 二维扰动波传播的数值模拟结果 Fig.1 Results of the numerical simulation for the propagation speed of 2-D disturbance waves |
表 1给出了稳定性分析及数值模拟的结果, Ue为能流速度, Ug为dω/dα的实部。
| 表 1 二维波的传播情况 Table 1 Propagation speed of 2-D waves |
|
|
从表 1可以看出, 能流速度Ue与Ug (dω/dα的实部)的差别是很大的, 即使是在中性曲线的端部, 即R为临界雷诺数5772, α, ω, dω/dα均为实数的情况, 能流速度Ue与Ug也有很大差别。而波的传播速度Ub与Ug是基本一致的, 这说明dω/dα的实部基本上能代表波的传播速度, 对于衰减率较大的波结论也是这样。
2.2 三维波的计算结果为了研究波沿不同方向的传播速度, 本文通过改变加入扰动波的方式针对三种特定的情况, 研究了三维波沿不同方向的传播速度。图 2给出了这三种特定情况计算域选取的示意图(示意图是在平行于平板的xoz平面中给出的)。
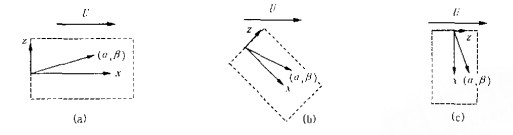
|
图 2 三维扰动波传播计算域选取的示意图 Fig.2 Sketch of domain of calculation for 3-D disturbance waves |
情况(1)研究的是三维波沿流向的传播速度, 坐标及计算域的选取如图 2 (a)。这时只在x方向有平均流, z方向平均流速为零, 而波数矢量不仅有流向(x方向)的分量, 而且有横向(z方向)的分量。由于研究的是扰动波沿流向的传播情况, 这就要求加入的扰动波的幅值沿横向均匀, 而沿流向是可以变化的。因此扰动波在横向上的波数β为实数, 在流向上的波数α可以为复数。在具体计算中, 初始平均流场为, u= (1-y2) ‚w=0, 扰动流场为零。然后在x=0处加入一个幅值沿横向均匀的T-S波, 这样就可以考察三维波沿流向的传播情况。
情况(2)研究的是三维波在沿与流向夹角为45°方向上的传播情况, 计算域与计算坐标的选取如图 2 (b)所示。计算时的初始平均流场为
情况(3)研究的是波沿横向的传播情况, 计算域与计算坐标的选取如图 2 (c)所示。初始平均流场为u=0‚w= (1-y2), 初始扰动场为零, 在x=0处加入沿流向(z方向)等幅值的T-S波, 就可以模拟波沿横向传播的情况。这时该T-S波在流向(z方向)波数β应为实数, 在横向(x方向)波数α可以为复数。
图 3给出了y=0.84处扰动波沿传播方向速度u的变化情况。

|
图 3 三维扰动波传播的数值模拟结果 Fig.3 Results of the numerical simulation for the propagation speed of 3-D disturbance waves |
表 2给出了计算的结果。其中Ug为∂ω/∂α的实部。从表 2可以看出对于三维扰动, Ue与Ug之间也有很大差别。从三维波的计算结果可以看出, 不管平均流方向与扰动波波数矢量的夹角如何, 波沿某一方向上的传播速度与波的频率ω沿该方向对波数的导数的实部是基本一致的, 也就是说如果α是x方向上的波数, 则∂ω/∂α的实部能代表波沿x方向的传播速度。
| 表 2 三维波的传播速度 (R=5772) Table 2 Propagation speed three-dimensional disturbance waves (R=5772) |
|
|
从二维波和三维波的计算中, 我们都可以看出, 波的能流速度Ue与波的传播速度是不一致的, 二者有较大的差别, 这表明流场中某一区域中能量的变化并不仅取决于上游传入该域的能量, 而和扰动波与平均流之间相互作用而导致的能量交换有关。这体现了非保守系统的特点。特别值得注意的是, 由稳定性分析, 对于中性曲线端点临界雷诺数, αi=0, dω/dα为实数, 看起来和保守系统相似。但实际上平均流与波之间仍有能量交换, 故Ue与Ug仍不相等。
3 结论从数值模拟结果看, 和水波中的群速度相当, 二维情况, dω/dα的实部, 三维情况, ∂ω/∂α及∂ω/∂β的实部, 可以近似地代表波的传播速度。在附录中我们给出了一个简单的物理模型以解释这一现象, 同时还给出了误差的估值。
附录:
设有两个波, 其频率相差一个小量Δω(为实数), 波数则相差Δα(可以是复数), 也是小量。在x=0处幅值相等, 这两个波之和可以表示为
| $ \begin{array}{l} \cos \left[ {\left( {{{{{ α} }}_r} + \Delta {{{{ α} }}_r}} \right)x - \left( {{{{{ ω} }}_r} + \Delta {{{{ ω} }}_r}} \right)t} \right]{e^{ - \left( {{{{{ α} }}_i} + \Delta {{{{ α} }}_i}} \right)x}} + \cos \left[ {{{{{ α} }}_r}x - {{{{ ω} }}_r}t} \right]{e^{ - {{{{ α} }}_i}x}}\\ \;\;\;\; = \left\{ {\cos \left[ {\left( {{{{{ α} }}_r} + \Delta {{{{ α} }}_r}} \right)x - \left( {{{{{ ω} }}_r} + \Delta {{{{ ω} }}_r}} \right)t} \right] + \cos \left[ {{{{{ α} }}_r}x - {{{{ ω} }}_r}t} \right]} \right\}{e^{ - {\alpha _i}x}}\\ \;\;\;\; + \cos \left[ {\left( {{{{{ α} }}_r} + \Delta {{{{ α} }}_r}} \right)x - \left( {{{{{ ω} }}_r} + \Delta {{{{ ω} }}_r}} \right)t} \right]\left[ {{e^{ - ({{{{ α} }}_r} + \Delta {{{{ α} }}_r})x}} - {e^{ - {\alpha _i}x}}} \right] \end{array} $ |
上式的第一项形成波包, 即“拍”, 可表示为
| $ 2\cos \left( {\left( {\Delta {{{{ α} }}_r}/2} \right)x - \left( {\Delta {{{{ ω} }}_r}/2} \right)t} \right)\cos \left[ {\left( {{{{{ α} }}_r} + \Delta {{{{ α} }}_r}/2} \right)x - \left( {{{{{ ω} }}_r} + \Delta {{{{ ω} }}_r}/2} \right)t} \right]{e^{ - {\alpha _i}x}} $ |
所形成的波包虽然沿x向会衰减或增长, 但有确定的传播速度Δωr/Δαr。而后一部分表示波从波包中漏出来的部分。波包的波长为2π/Δαr。一个波长内漏出去的波能量为
| $ \begin{array}{l} \Delta E = \frac{1}{2}\int_{\frac{{{{ π} }}}{{\Delta {{{{ α} }}_r}}}}^{\frac{{{{ π} }}}{{\Delta {{{{ α} }}_r}}}} {{{\left\{ {\cos \left[ {\left( {{{{{ α} }}_r} + \Delta {{{{ α} }}_r}} \right)x - \left( {{{{{ ω} }}_r} + \Delta {{{{ ω} }}_r}} \right)t} \right]\left[ {{e^{ - \left( {{{{{ α} }}_i} + \Delta {{{{ α} }}_i}} \right)x}} - {e^{ - {{{{ α} }}_i}x}}} \right]} \right\}}^2}} {\rm{d}}x\\ \;\;\;\;\;\; \approx \frac{1}{4}\int_{ - \frac{{{{ π} }}}{{\Delta {{{{ α} }}_r}}}}^{\frac{{{{ π} }}}{{\Delta {{{{ α} }}_r}}}} {{{\left[ {{e^{ - \left( {{{{{ α} }}_i} + \Delta {{{{ α} }}_i}} \right)x}} - {e^{ - {{{{ α} }}_i}x}}} \right]}^2}} {\rm{d}}x\\ \;\;\;\;\;\; = \frac{1}{4}\left[ {\frac{{ sh \left[ {2{{{ π} }}\left( {{{{{ α} }}_i} + \Delta {{{{ α} }}_i}} \right)/\Delta {\alpha _r}} \right.}}{{\left( {{{{{ α} }}_i} + \Delta {{{{ α} }}_i}} \right)}} - 2\frac{{ sh \left[ {2{{{ π} }}\left( {{{{{ α} }}_i} + \Delta {{{{ α} }}_i}/2} \right)/\Delta {{{{ α} }}_r}} \right.}}{{\left( {{{{{ α} }}_i} + \Delta {{{{ α} }}_i}/2} \right)}} + \frac{{ sh \left[ {2{{{ π} }}{{{{ α} }}_i}/\Delta {{{{ α} }}_r}} \right]}}{{{{{{ α} }}_i}}}} \right] \end{array} $ |
而波包内的波能量为
| $ \begin{array}{l} E = \frac{1}{2}\int_{\frac{{{{ π} }}}{{\Delta {{{{ α} }}_r}}}}^{\frac{{{{ π} }}}{{\Delta {{{{ α} }}_r}}}} {{{\left\{ {2\cos \left[ {\left( {\Delta {{{{ α} }}_r}/2} \right)x - \left( {\Delta {{{{ ω} }}_r}/2} \right)t} \right]\cos \left[ {\left( {{{{{ α} }}_r} + \Delta {{{{ α} }}_r}/2} \right)x - \left( {{{{{ ω} }}_r} + \Delta {{{{ ω} }}_r}/2} \right)t} \right]{e^{ - {\alpha _i}x}}} \right\}}^2}} {\rm{d}}x\\ \;\;\;\; \approx \frac{1}{2}\int_{\frac{{{{ π} }}}{{\Delta {{{{ α} }}_r}}}}^{\frac{{{{ π} }}}{{\Delta {{{{ α} }}_r}}}} {{e^{ - 2{\alpha _i}x}}} dx = \frac{1}{2} sh\left[ {2{{{ π} }}{\alpha _i}/\Delta {\alpha _r}} \right]/{\alpha _i} \end{array} $ |
如果αi≠0, 取两个很靠近的波, 设Δαi≪αi, 则从波包中漏出去的波能量与总的波能量之比
| $ \begin{array}{l} \frac{{\Delta E}}{E} = \frac{1}{2}\left[ {\frac{{ sh\left[ {2{{{ π} }}\left( {{{{{ α} }}_i} + \Delta {{{{ α} }}_i}} \right)\Delta {{{{ α} }}_r}} \right]}}{{\left( {1 + \Delta {{{{ α} }}_i}/{{{{ α} }}_i}} \right)sh\left[ {2{{{ π} }}{{{{ α} }}_i}/\Delta {{{{ α} }}_r}} \right]}} - 2\frac{{ sh\left[ {2{{{ π} }}\left( {{{{{ α} }}_i} + \Delta {{{{ α} }}_i}} \right)\Delta {{{{ α} }}_r}} \right]}}{{\left( {1 + \Delta {{{{ α} }}_i}/{{{{ α} }}_i}} \right)sh\left[ {2{{{ π} }}{{{{ α} }}_i}/\Delta {{{{ α} }}_r}} \right]}} + 1} \right]\\ \;\;\;\;\;\; \approx \frac{1}{2}\left[ {1/\left( {1 + \frac{{\Delta {{{{ α} }}_i}}}{{{{{{ α} }}_i}}}} \right) - 2/\left( {1 + \frac{1}{2}\frac{{\Delta {{{{ α} }}_i}}}{{{{{{ α} }}_i}}}} \right) + 1} \right] \approx \frac{1}{4}{\left( {\frac{{\Delta {{{{ α} }}_i}}}{{{{{{ α} }}_i}}}} \right)^2} \end{array} $ |
是一个小量。
如果αi=0, 则从波包中漏出去的波能量、总的波能量分别为
| $ \Delta E \approx \frac{1}{2}\left[ {\frac{{ sh\left[ {2{{{ π} }}\Delta {\alpha _i} + /\Delta {\alpha _r}} \right]}}{{2\Delta {\alpha _i}}} - 2\frac{{ sh\left[ {{{{ π} }}\Delta {\alpha _i}/\Delta {\alpha _r}} \right]}}{{\Delta {\alpha _i}}} + \frac{{{{ π} }}}{{\Delta {\alpha _r}}}} \right],\;\;\;\;E \approx \frac{{{{ π} }}}{{\Delta {\alpha _r}}} $ |
两者之比为
| $ \frac{{\Delta E}}{E} \approx \frac{1}{2}\left[ {\frac{{ sh\left[ {2{{{ π} }}\Delta {\alpha _i} + /\Delta {\alpha _r}} \right]}}{{2{{{ π} }}\Delta {\alpha _i}/\Delta {\alpha _r}}} - 2\frac{{ sh\left[ {{{{ π} }}\Delta {\alpha _i}/\Delta {\alpha _r}} \right]}}{{{{{ π} }}\Delta {\alpha _i}/\Delta {\alpha _r}}} + 1} \right] \approx \frac{1}{6}{\left( {\frac{{{{{ π} }}\Delta {\alpha _i}}}{{\Delta {\alpha _r}}}} \right)^2}。$ |
如果Δαi/Δαr≤0.1, 就有ΔE/E=0.016, 漏出去的波能与总的波能量之比也是一个小量。漏出去的波能与总的波能量之比可以看成是用dω/dα的实部确定波包传播速度的误差。上边的分析可以说明, 波包的传播速度和dω/dα的实部差别很小。而如果Δαi=0, 则Δω/Δα=Δωr/Δαr为实数, 误差等于零, 与Gaster研究的情况相当。图 4给出了某一时刻在保守系统、非保守系统但Δαi=0的情况及一般的非保守系统中, 两个波叠加得到的波包的波形。
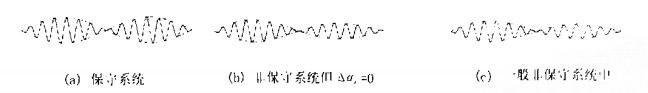
|
图 4 某一时刻波包的波形 Fig.4 Wave form of wave packets at a certain time |
| [1] |
Lighthill J. Waves in flow[M]. Cambridge, 1978.
|
| [2] |
Gaster M. Propagation of linear wave packets in laminar boundary Layers[J]. AIAA Journal, 1981(4): 419-423. |
| [3] |
Cebeci T, Stewartson K. On stability and transition in three dimensional flows[J]. AIAA Journal, 18: 398-405. DOI:10.2514/3.50772 |
| [4] |
Radeztsty R H, Reibert M S & Saric W S. Development of stationary cross-flow vortices on a swept wing [R]. AIAA 94-2373, 1994.
|
| [5] |
Karniadakis GE, Israeli M, Orzag SA. High-order splitting methods for the incompressible. Navier-Stokes equations[J]. J. Compu. Phys, 1991, 97: 414-443. DOI:10.1016/0021-9991(91)90007-8 |
| [6] |
Zhongmin Xiong, Guocan Ling. Compact finite difference-fourier spectral method for three-dimensional incompressible Navier-Stokes equations[J]. Acta Mechanica Sinica (English series), 1996, 12(4): 1-11. |
 2002, Vol. 20
2002, Vol. 20
