| 基于组合权-模糊数学的多金属矿区资源开发利用效率评价 |
矿产资源作为提升国民经济水平的物质保障,存在开采不可再生和初始赋存量有限的特点。尽管我国在矿产资源的采选技术方面有了长足的进步,但仍无法完全避免多金属矿区共伴生有用组分的浪费现象。国家一直提倡节约资源,提高资源利用效率和效益。所以,针对多金属矿区开展资源开发效率评价研究,找出资源开发过程中存在的问题显得尤为必要[1]。
多金属矿区资源开发利用效率评价作为一项复杂的系统工程,其评价指标体系的科学性、评价方法的合理性是评价的关键之处。裴志涛等[2]选用BP神经网络法以各行业用水效率为评价指标,进行量化处理后对水资源的综合利用情况进行了评价。丁其光等[3]以“三率”水平、“三废”回收率等构建了评价体系,对指标量化计算进行解释,并以某多金属矿为评价对象进行了实践。赵军伟等[4]从资源自身利用情况、社会效应和开发利用限制考虑,建立了评价体系。常用的评价方法主要有BP神经网络、AHP法、DEA法和灰色关联度评价等。本文从矿石利用情况、环境影响、开发投入和经济效益四方面入手,构建了评价体系,以组合权—模糊数学为原理,提出了一套适用于多金属矿区的资源利用效率评价方法。
1 评价指标体系的构建及各指标权值的确定 1.1 评价指标体系的建立矿区资源的开发利用效率就是矿山企业采选后所得产品和它所引起的多种经济效应、社会和环境影响与所动用的资源储量之比,即消耗单位矿产资源带来的经济产出,能够从本质上反应出单位资源所产生的功效和影响[5]。所以,评价矿产资源的开发利用效率,应当从其自身所产生的多方面功效来入手,即矿山企业动用单位储量的资源所带来的人力和材料消耗、经济价值、社会影响和环境影响等。
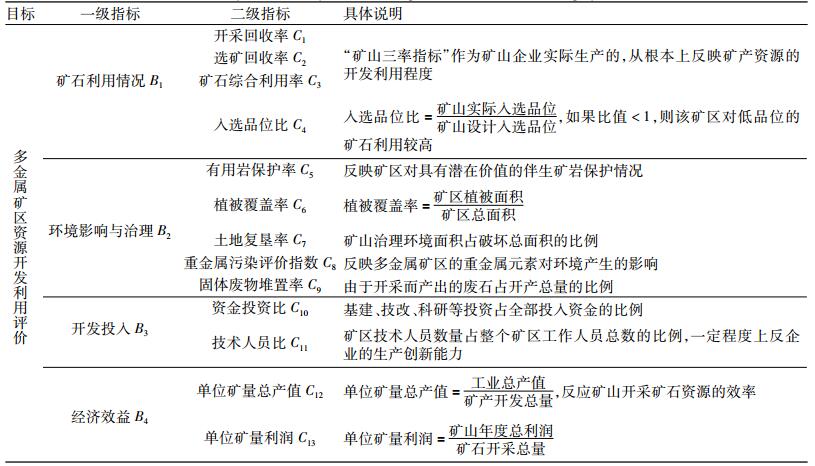
影响多金属矿区资源开采利用的因素众多。往常的矿产资源开发利用效率评价只考虑资源的“三率”情况,忽略了矿产资源开发所必须的投入和环境影响与治理。从国家推进建设生态文明社会和加强资源综合利用的角度出发,评价指标的选取应当遵循完整、科学及可操作的原则。因此从资源开发的矿石利用情况、矿山环境影响和技术资金投入等方面着手,构建了适用于多金属矿区矿石开发利用效率的评价体系[5],见表 1。
| 表 1 多金属矿区资源开发利用效率评价体系 Table 1 The efficiency evaluation system of the exploitation and utilization of polymetallic ore district |
 |
1.2 计算各指标权重
在多金属矿区资源的开发利用效率评价中,指标权值的合理与否对最终的评价结果可靠性起着关键作用。专家法确定权重,充分采纳了专家观点,但是其主观性强的特点不可避免;客观赋权法根据数学理论进行计算,但未能结合专家经验。因此,选择将专家评分法得到的权重we与熵值法计算的权重wc进行加权平均,得到既包含专家意见又能体现数据规律的组合权重。
(1) 熵值法确定权值wc
熵值法从各指标数值自身规律角度入手,由计算得到的信息熵确定指标对映权值[6]。
比如有M个被评估矿山各自对映的n个指标值构成了集合S
S={x1, x2, …, xM}, xi∈Rn
则计算方法如下:
第一步:处理原始数据。因为计算模型中所使用的指标都是正向指标,故选择公式(1)来计算:
| $ {y_{ij}} = \frac{{{x_{ij}}}}{{\max {x_j}}} $ | (1) |
其中,xij为第j个指标的第i个评价对象的值;maxxj是第j个指标的最大值;yij为极差化处理后所得。
第二步:比重法求解评价值pij。
| $ {p_{ij}} = \frac{{{y_{ij}}}}{{\sum\limits_{i = 1}^m {{y_{ij}}} }}, \left( {i = 1, 2, \cdots, m;j = 1, 2, \cdots, n} \right) $ | (2) |
第三步:求解j所对映的差异性系数G和输出熵E。
| $ {E_j} =-k\sum\limits_{i = 1}^m {{p_{ij}}\ln {p_{ij}}} $ | (3) |
| $ {G_j} = 1-{E_j}, j = 1, 2, \cdots, n $ | (4) |
第四步:计算各个指标的权重
wc=(w1, w2, …, wn)T
其中第j个指标的权重
| $ {w_j} = \frac{{{G_j}}}{{\sum\limits_{j = 1}^n {{G_j}} }}, j = 1, 2, \cdots, n $ | (5) |
(2) 确定组合权值w
熵值法所得客观权重仅体现了各评价指标在竞争上的强烈情况,无法代表各指标在现实中的重要程度。当被评价单元的某项指标在数值上偏差越大,熵值越小,则其提供的有效信息量较大,权重也会越大;而某项指标在数值上偏差越小,熵值越大,其提供的信息量较小,权重也就越小。而专家们则结合实际问题从自身经验角度来给各项评价指标进行排序,尽管与熵值法所确定的权重有一定差异,却减小了与实际状况相违背的程度。所以,将二者相结合得到的权重排序将更加合理。
采用专家打分得到具有专家经验的权值we再结合熵值法求得客观权值wc,经过线性组合得到最终的权值公式如下:
| $ w = \alpha {w^e} + \left( {1-\alpha } \right){w^c} $ | (6) |
其中, α为主观偏好系数。在此选取α=0.5,得组合权计算公式为:
| $ w = 0.5{w^e} + 0.5{w^c} $ | (7) |
模糊综合评价法运用模糊数学原理,对各评价指标进行模糊合成,将本身难定量表示的指标进行量化处理,然后选择合适的隶属度函数求得各指标的隶属度情况来得到评价结果[7]。基本步骤如下:
(1) 建立评价因素集。
U={C1, C2, C3, …, Cn}
(2) 建立评价结果集。根据被评价对象的实际情况将评语划分为个等级,分别记为v1,v2,…,vm,这m个等级构成一个评语的有限集合
V={v1, v2, …, vm}
(3) 确定模糊判断矩阵。模糊集V实质上是V→[0, 1]的函数。选择的隶属度函数公式如下:
| $ {r_1} = \left\{ {\begin{array}{*{20}{c}} 1&{{x_i} \le {v_1}}\\ {\frac{{{v_2}-{x_i}}}{{{v_2}-{v_1}}}}&{{v_1} \le {x_i} \le {v_2}}\\ 0&{{x_i} \ge {v_2}} \end{array}} \right. $ | (8) |
| $ {r_2} = \left\{ {\begin{array}{*{20}{c}} {1-{r_1}}&{{v_1} \le {x_i} \le {v_2}}\\ {\frac{{{v_3}-{x_i}}}{{{v_3}-{v_2}}}}&{{v_2} \le {x_i} \le {v_3}}\\ 0&{{x_i} \le {v_1}, {x_i} \ge {v_3}} \end{array}} \right. $ | (9) |
| $ {r_j} = \left\{ {\begin{array}{*{20}{c}} {\frac{{{x_i}-{v_{j-1}}}}{{{v_j}-{v_{j - 1}}}}}&{{v_{j - 1}} \le {x_i} \le {v_j}}\\ {\frac{{{v_{j + 1}} - {x_i}}}{{{v_{j + 1}} - {v_j}}}}&{{v_j} \le {x_i} \le {v_{j + 1}}}\\ 0&{{x_i} \le {v_{j - 1}}, {x_i} \ge {v_{j + 1}}} \end{array}} \right. $ | (10) |
式中:xi—指标的实际值;i为评价体系中的每个评价指标;vj—评价指标的第j个分级阈值;rj—第j级评价指标的隶属度,且对任一因素都有
(4) 结合确定的权重向量进行模糊合成。根据每个指标的权重和评分等级标准,计算各区评价指数结果。
3 某多金属矿区矿产资源开发利用效率评价 3.1 某多金属矿区概况某多金属矿区位于内蒙古地区,该矿区采用露天开采方式回采矿石。主采矿山有三座,并且形成了以铁矿石为主、稀土等伴生组分综合回收的采选原则,但仍有部分有经济价值的元素未回收利用。本次评估对象为该区主采的三座矿山,在此依次编为KS1、KS2、KS3。
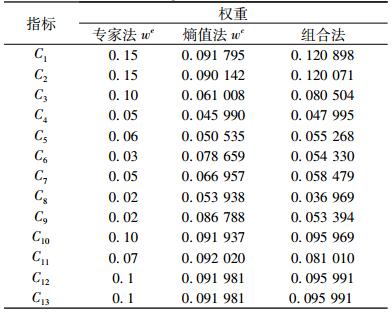
3.2 某多金属矿区组合权的确定本文中评价单元有三个,各项指标数值均有差异能够突出各自的竞争强度,所以熵值法所得权重可以使用。we为专家打分得到具有专家经验的权值,wc为熵值法所得客观权值,由式(7)计算得到了最终的权重,具体结果见表 2。
| 表 2 评价指标权重 Table 2 Weight of evaluation index |
 |
3.3 评价对象的指标数据获取
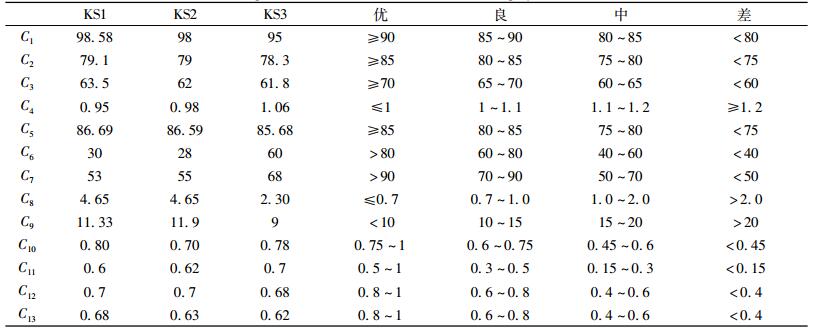
根据现有行业标准及工业指标等,建立了多金属矿区资源开发利用效率评价的评分标准。由于一些指标目前尚无确切的行业标准,所以在此将这些指标值做归一化处理。评价对象的各指标具体数值见表 3。
| 表 3 某多金属矿区资源各指标量化数据及评分标准 Table 3 The quantitative data and score criterion of the polymetallic ore district |
 |
3.4 进行模糊综合评价
(1) 因素集的建立
因素集为
U={C1, C2, C3, …, C13}
(2) 评价集的建立
根据表 3中的评分标准,将评价结果定为4种。评价集为
V={v1, v2, v3, v4}={优,良,中,差}
(3) 隶属度函数的计算
使用公式(8)、(9)、(10)计算评价指标对于评价等级的隶属度,依次生成某多金属矿区3座矿山的隶属函数矩阵R1、R2、R3。如下:
| $ {R_1} = {\left[{\begin{array}{*{20}{c}} {1}&{0}&{0}&{1}&{1}&{0}&{0}&{0}&{0.734}&{0.04}&{0.2}&{0.5}&{0.4}\\ {0}&{0.18}&{0.3}&{0}&{0}&{0}&{0.15}&{0}&{0.266}&{0.96}&{0.8}&{0.5}&{0.6}\\ {0}&{0.82}&{0.7}&{0}&{0}&{0}&{0.85}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{1}&{0}&{1}&{0}&{0}&{0}&{0}&{0} \end{array}} \right]^T} $ |
| $ {R_2} = {\left[{\begin{array}{*{20}{c}} {1}&{0}&{0}&{1}&{1}&{0}&{0}&{0}&{0.62}&{0.08}&{0.2}&{0.5}&{0.15}\\ {0}&{0.18}&{0.3}&{0}&{0}&{0}&{0.25}&{0}&{0.38}&{0.92}&{0.8}&{0.5}&{0.85}\\ {0}&{0.82}&{0.7}&{0}&{0}&{0}&{0.75}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{1}&{0}&{1}&{0}&{0}&{0}&{0}&{0} \end{array}} \right]^T} $ |
| $ {R_3} = {\left[{\begin{array}{*{20}{c}} {1}&{0}&{0}&{0.6}&{1}&{0}&{0}&{0}&{0.52}&{0.12}&{0.2}&{0.4}&{0.4}\\ {0}&{0.26}&{0.16}&{0.4}&{0}&{0}&{0.10}&{0}&{0.48}&{0.88}&{0.8}&{0.6}&{0.6}\\ {0}&{0.74}&{0.84}&{0}&{0}&{0}&{0.9}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{1}&{0}&{1}&{0}&{0}&{0}&{0}&{0} \end{array}} \right]^T} $ |
(4) 评价结果计算
该多金属矿区矿石资源开发利用效率评价集V的隶属度矩阵为
| $ B = w{R_i}, i = 1, 2, 3 $ | (11) |
把表 2的计算结果代入式(11)中,得到的隶属度矩阵分别为
B1={0.369 80.331 30.204 50.091 3}
B2={0.343 50.363 40.198 70.091 3}
B3={0.337 20.359 20.209 10.091 3}
3.5 评价结果及分析根据计算结果可得,某多金属矿区,KS1优的隶属度最高,KS2、KS3良的隶属度最高,所以评价结果为KS1优,KS2、KS3良。此外,根据组合权值的大小得出在资源开发利用中开采回收率、选矿回收率及资金投资比对矿山资源利用效率影响较大,企业经济效益以及对社会经济的影响也是不可忽略的因素。矿产资源的“三率”是资源开发利用效率的核心组成部分。所以,加大资源开发的科研投入和人才储备,从长远角度科学规划多金属矿区资源的开发方案,实现多金属矿区资源集约化开发利用是未来的发展方向。
KS1的评价结果最佳,资源整体开发利用效率较高,对具有潜在经济价值的矿岩保护良好。矿山由于生产服务年限已经较长,目前已进入深凹开采,矿方合理投资采用了汽车—破碎站—胶带联合运输方式,降低了运输成本,提高了企业经济效益。
KS2的总体评价结果介于其它二者之间。矿石综合利用率较低,主要原因是深部矿体厚度逐渐变小,开采难度加大;伴生组分含量增加,但无法大规模利用。该区地面废岩堆置率最高,矿区环境不容乐观。建议矿区加大勘探投入,查明该区深部资源赋存状况,研究伴生组分大规模开发的经济性。
KS3资源利用情况较低。区内矿石平均品位偏低增加了选矿成本,加之外部市场的影响,减少了单位矿量利润;矿坑内降尘措施有效,地面剥离岩石堆置合理,矿区环境治理有序。增加选矿技术投入,降低氧化矿入选品位,是该区提高资源利用效率的关键。
4 结论针对多金属矿区构建的资源开发利用效率评价指标体系涵盖了资源利用状况、环境影响、开发投入以及经济效益四个方面,能够客观地反映多金属矿区的资源开发实际状况。指标体系易于量化,组合权法得到的权值更加可靠,模糊评价法便于操作,适用于伴生组分无法大量利用的多金属矿区进行资源开发利用效率的综合评价。但仍有部分难以量化的外部影响未考虑在内,这将是日后完善评价方法的研究重点。
针对我国多金属矿区现状,应当加大资源的勘查力度和开发投入,完善暂时无法使用的伴生资源保护措施,在科学管理的基础上,以最低的储量、物料消耗,实现共伴生资源的集约化大规模综合利用,使资源利用功效最大化,同时降低环境的破坏和避免伴生资源的浪费,达到资源可持续利用的目的。
| [1] |
鹿爱莉, 孙志伟, 马静. 国内外矿产资源开发利用技术经济评价[J]. 中国矿业, 2008, 17(3): 11-18. |
| [2] |
裴志涛, 何俊仕. 基于BP神经网络的水资源利用效率评价方法研究[J]. 中国农村水利水电, 2013(5): 30-32. |
| [3] |
丁其光, 徐明. 矿产开发利用效率评价指标及方法初探[J]. 矿产综合利用, 2012(1): 53-55. |
| [4] |
赵军伟, 郭敏, 赵恒勤. 矿产资源开发利用效率评价构想[J]. 中国矿业, 2012, 21(8): 60-63. |
| [5] |
冯安生, 许大纯, 吕振福. 矿产开发利用效率指标研究[J]. 矿产保护与利用, 2013(6): 1-7. |
| [6] |
冯安生, 许大纯. 矿产资源新"三率"指标研究[J]. 矿产保护与利用, 2012(4): 4-7. |
| [7] |
郭显光. 改进的熵值法及其在经济效益评价中的应用[J]. 系统工程理论与实践, 1998, 18(12): 98-102. |
| [8] |
杜栋, 庞庆华, 吴炎. 现代综合评价方法与案例精选[M]. 北京: 清华大学出版社, 2008.
|
| [9] |
吴和平, 吴玲, 何艳梅. 矿产资源优化利用与矿业可持续发展研究[J]. 矿产保护与利用, 2007(2): 1-6. |
 2017
2017 
