| 钛渣喷动床沸腾氯化气固两相流数值模拟 |
国内沸腾氯化制备TiCl4的工艺使用含TiO2的原料,因氯化工艺的不同要求,原料中TiO2含量78%~92%不等[1],攀西地区钒钛磁铁矿的品位较低(TiO2≈10%)而钙镁含量较高(CaO+MgO≈5%~7%), 不能满足沸腾氯化工艺对原料品位的要求。经电炉熔炼得到的钛渣中TiO2的品位达到80%以上,因此在品位上满足沸腾氯化工艺的要求,但是电炉熔分的钛渣钙镁含量高达7%~11%,沸腾氯化过程中易造成床层黏结失流,流态化过程顺行困难[2-4]。为实现沸腾氯化处理攀西地区高钙镁的钛资源, 前人已经做了大量研究,结果表明:无筛板沸腾氯化炉处理高钙镁含量的钛渣避免了黏结失流造成筛板孔眼易堵塞的问题,处理高钙镁钛渣的能力明显优于筛板沸腾氯化炉[5]。喷动床作为一种典型的无筛板气固流态化反应器,床层底部高压来流提供能量,在床层内部形成喷射区、喷泉区和环稀区的循环气固两相流[6]。因此喷动流化床作为钛渣沸腾氯化反应器制备TiCl4是目前主流工艺之一。但实际生产中,喷动床床层内部固相和气相表现出典型的复杂性和非线性,这容易造成床层内部结焦等问题,严重影响了大型喷动流化床的顺行。为了解决大型床层内部结焦等问题, 实现喷动床沸腾氯化的顺行,进一步研究床层内部气固两相流的流动特性是必要的。采用实验室手段去研究床层内部气固两相流问题是必不可少的,但是由于喷动床沸腾氯化设备的大型化和复杂化,并且氯化气体为氯气,使得实验室研究存在投资高、耗时长、危险系数高等问题,随着计算机技术的飞速发展,国内外数值模拟研究气固两相流逐渐成为主流方法之一。因此本文结合攀枝花钛渣的物性参数,采用计算数值模拟仿真技术对喷动床沸腾氯化床层内部气固两相流进行数值模拟,了解床层内部气固两相流特征,为解决实际生产中的问题提供指导。
本文采用数值模拟技术研究喷动床沸腾氯化工艺中气固两相流的流动特征,以最小喷吹速度的经验公式、气固两相流的基本方程以及气固相间的耦合机制为基础,建立了钛渣喷动床沸腾氯化床层内部钛渣和氯气两相流的数学模型。数学模型结合攀西地区钛渣的物性通过Fluent商业软件对钛渣气固两相流进行了数值模拟计算。数值模拟确定钛渣喷动床沸腾氯化适宜的实际操作气速;钛渣和氯气两相的云图和速度矢量分析明确了床层气固两相流流动特征,找到了床层中密相区和稀相区的分布,为实际设计反应器避免出现密相区提供了方向。数值模拟结果确定钛渣喷动床沸腾氯化床层内部的最大喷吹高度。因此本文数值模拟结果对喷动床钛渣沸腾氯化操作气速工艺参数控制、黏结失流控制和反应器设计等方面有明确的意义。
1 钛渣喷动床沸腾氯化气固两相流数学模型钛渣喷动床沸腾氯化气固两相流的数学模型是以气固两相流的欧拉双方程、传统最小喷吹速度的经验以及气固相间的耦合机制等多方面来确定的。
1.1 欧拉双流体模型欧拉双流体模型是将颗粒作为拟流体,认为固相和流体相共同存在且互相渗透的连续介质模型[7]。钛渣喷动床沸腾氯化气固两相主要考虑为氯气(气相)和钛渣(固相),描述气—固两相流的流体连续和动量控制方程如下:
连续方程:
气相:
| $ \frac{{\partial \left( {{\varepsilon _g}{\rho _g}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\varepsilon _g}{\rho _g}\overrightarrow {{u_g}} } \right) = 0 $ | (1) |
固相:
| $ \begin{array}{c} \frac{{\partial \left( {\left( {1 - \varepsilon g} \right)\rho p} \right)}}{{\partial t}} + \\ {\rm{ }}\nabla \cdot \left( {\left( {1 - \varepsilon g} \right)\rho g\overrightarrow {ug} } \right) = 0 \end{array} $ | (2) |
动量方程:
气相:
| $ \begin{array}{c} \frac{{\partial \left( {{\varepsilon _g}{\rho _g}{u_g}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\varepsilon _g}{\rho _g}\overrightarrow {{u_g}} \overrightarrow {{u_g}} } \right) = {\rm{ }}\\ \nabla \cdot \left( {{\varepsilon _g}{\tau _g}} \right) + {\varepsilon _g}{\rho _g}g - {\varepsilon _g}\nabla P - \beta (\overrightarrow {{u_g}} - \overrightarrow {{u_p}} ) \end{array} $ | (3) |
固相:
| $ \begin{array}{c} \frac{{\partial \left( {\left( {1 - {\varepsilon _g}} \right){\rho _g}{u_g}} \right)}}{{\partial t}} + \nabla \cdot \left( {\left( {1 - {\varepsilon _g}} \right){\rho _g}\overrightarrow {{u_p}} \overrightarrow {{u_p}} } \right) = \\ {\rm{ }}\nabla \cdot \left( {1 - {\varepsilon _g}} \right){\tau _p} + \left( {1 - {\varepsilon _g}} \right){\rho _p}g - \\ \left( {1 - {\varepsilon _g}} \right)\nabla P + \beta \left( {\overrightarrow {{u_g}} - \overrightarrow {{u_p}} } \right) + \nabla {P_p} \end{array} $ | (4) |
合理的曳力模型被用于封闭动量方程(3)和(4)中的气固相间阻力系数。在众多的气固两相流的模型中,气固两相之间的耦合关系和固体颗粒的曳力计算对模拟结果有明显影响,曳力计算主要是方便做气固相作用的定量计算[8]。根据曳力模型由来和不同的推导方式,曳力模型主要归纳为以下三种:(1)表观气速和床层膨胀相关参数的R-Z方程形式的关联式,如Felice模型[9];(2)根据试验数据关联得到的经验或半经验模型,如Wen-Yu模型[10],该方程适合气体体积分数大于0.8的情况、而体积分数小于0.8则采用Ergun模型[11];(3)基于一定的气固作用机理,通过格子Boltzmann方法推导得到的模型,如Koch-Hill[12]以及R. Beetstra[13]模型。本文涉及到气固两相流密集相的流动特征的数值模拟,床层流动特征与反应器以及颗粒物性有极大的相关性,为了成功模拟喷动床各个分区的特征,需要解决高体积分数和低体积分数的情况,因此本文采用Wen -Yu模型和Ergun方程的联合的Gidaspow模型作为耦合气固相的曳力模型。该模型能够在计算颗粒体积分数较小的密集相的气固两相流流动情况,定量预测床内气固两相流流动都取得了比较好的结果[14],同时,林亮成[15]采用fluent软件结合Gidaspow模型成功的模拟出了玻璃珠气固两相的流体动力学特征。因此,选择该曳力模型进行模拟研究。Gidaspow曳力模型如下:
气固相间曳力相互作用耦合相关系数β为一个函数表达式:
| $ \begin{array}{c} \beta = 150\frac{{{{\left( {1 - {\varepsilon _g}} \right)}^2}{\mu _g}}}{{{\varepsilon _g}{{\left( {{\varphi _p}{d_p}} \right)}^2}}} + \\ 1.75\frac{{\left( {1 - {\varepsilon _g}} \right){\rho _g}\left| {\overrightarrow {{u_g}} - \overrightarrow {{u_p}} } \right|}}{{{\varphi _p}{d_d}}}\\ \left( {{\varepsilon _g} < 0.8} \right) \end{array} $ | (5) |
| $ \begin{array}{c} \beta = \frac{3}{4}{C_D}\frac{{{\varepsilon _g}\left( {1 - {\varepsilon _g}} \right){\rho _g}\left| {\overrightarrow {{u_g}} - \overrightarrow {{u_p}} } \right|}}{{{\varphi _p}{d_d}}}\varepsilon {g^{ - 2.65}}\\ \left( {{\varepsilon _g} > 0.8} \right) \end{array} $ | (6) |
曳力系数CD表示为:
| $ {C_D} = \left\{ {\begin{array}{*{20}{c}} {\frac{{24}}{{R{e_p}}}\left[ {1 + 0.15{{\left( {{\varepsilon _g}R{e_p}} \right)}^{0.687}}} \right]}&{\left( {R{e_p} > 1000} \right)}\\ {0.44}&{\left( {R{e_p} < 1000} \right)} \end{array}} \right. $ | (7) |
式中(1-7)符号说明:
ε:床层空隙率;ρ:密度,kg/m3;u:速度,m/s;τ:时间,s;P:压力,Pa;β:气固相间曳力,N;φ:钛渣球形度;μ:黏性系数;d:颗粒粒径,m;Re:雷诺准数;CD:曳力系数。
下标:p:固相,g:气相。
1.2 钛渣喷动流态化几何模型根据本次试验的要求,现对试验所用喷动床模型的设计作如下设计与处理:
(1) 为更好的观察气相、固相的运动规律,采用准二维喷动床模型求解。
(2) 喷动床高600 mm,宽200 mm,厚为20 mm,锥体底部倒角为60°,气体入口直径取20 mm。喷动床几何模型如图 1所示。
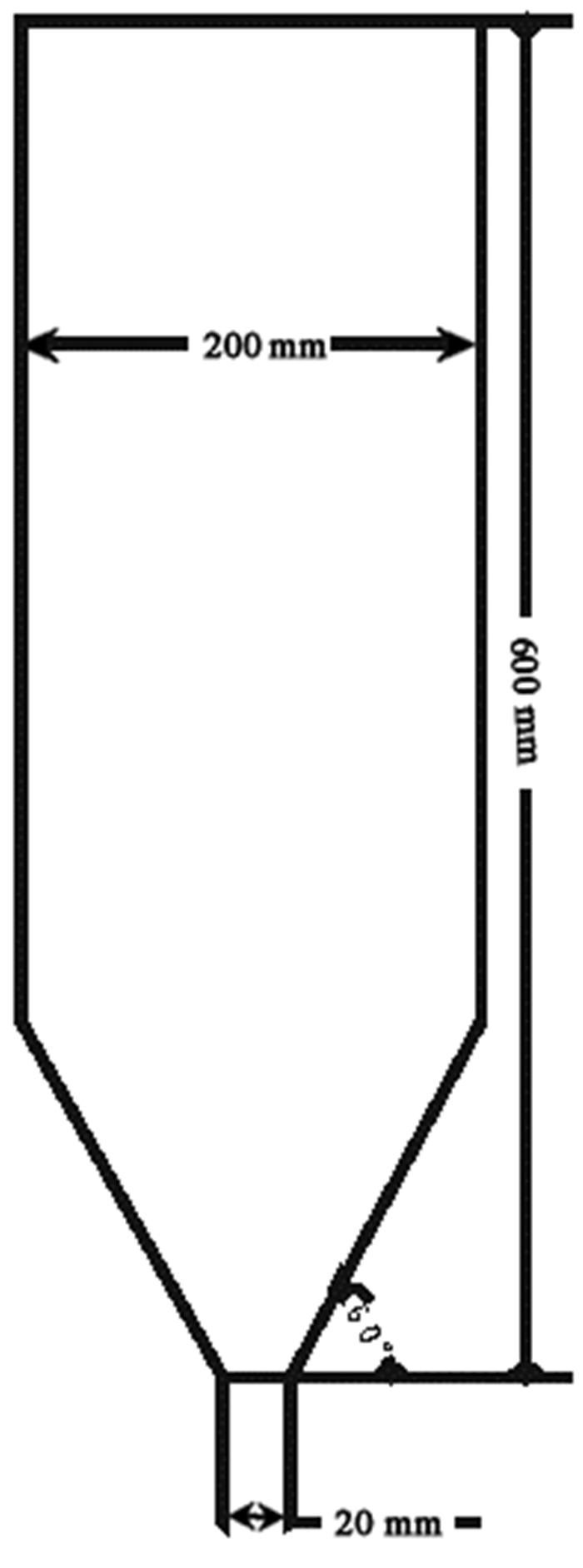 |
| 图 1 喷动床二维几何模型 Fig.1 2D model of spouted fluidized-bed |
1.3 模型计算边界条件 1.3.1 双流体模型计算边界条件
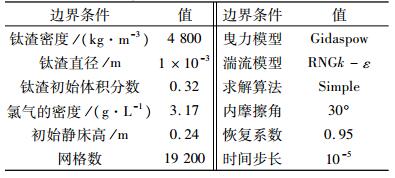
采用Fluent 6.3.26软件对钛渣喷动床沸腾氯化气固两相流进行数值模拟,需要结合钛渣物性和相关边界条件。本文以攀西地区钛渣的物性参数作为研究基础,相关物性参数和边界条件如表 1。
| 表 1 模拟计算的边界条件 Table 1 Boundary conditions for simulation calculation |
 |
1.3.2 最小喷吹速度理论计算
传统的最小喷吹速度和最大喷吹高度的经验计算公式和计算所得的最小喷吹速度、最大喷吹高度分别见表 2、表 3。
| 表 2 最小喷吹速度 Table 2 Minimum spouting velocity |
 |
| 表 3 最大喷动高度 Table 3 Maximum spoutable bed height |
 |
表 2和表 3中公式符号说明:Ums:最小喷吹速度;H:静床高;dp:颗粒直径;Dc:喷动床内径,Di:喷嘴直径;ρp:颗粒密度;ρf:气体密度;umf:最小流化速度;ut:最大速度;C1和C2:常数;μR:气体黏度;Hm:最大喷吹高度;Ar:阿基米德常数。
2 钛渣喷动床沸腾氯化数值模拟与结果分析 2.1 基于Fluent软件的数值模拟方法数值模拟采用Fluent 6.3.26计算流体力学软件包,数学模型是以双流体数学模型、曳力模型(Gidaspow模型)为基础结合钛渣相关物性参数和边界条件进行数值计算。模型的离散使用有限容积差分法, 动量差分格式为二阶迎风格式。计算方式为压力基隐式非稳态求解,具体应用Simple算法,黏性模型选择RNGk-ε。在壁面处,气—固两相流使用无滑移边界条件,体积分数差分格式采用QUICK格式。计算时连续性方程X和Y两个方向的动量方程残差精度为10-4,湍动能和湍动能耗散率残差精度为10-3,其他参数取值见表 1~表 3。
2.2 最小喷动速度数值模拟分析与讨论 2.2.1 最小喷动速度下的云图分析图 2是喷动床气固两相流典型的流动特征,通常将内部流场分为三个区:喷射区、环隙区和喷泉区。流体经由位于圆锥形底部中心处的喷嘴垂直向上射入,形成一个随流体流速的增高而逐渐向上延伸的射流区。当流体喷射速率足够高时,该射流区将穿透床层而在颗粒床层内产生一个迅速穿过床层中心向上运动的稀相气固流栓(喷射区)。当这些被流体射流夹带而高速向上运动的粒子穿过环绕其四周缓慢向下移动的颗粒床层(环隙区)而升至高过床层表面的某一高度时,由于流体速度的骤然减小,颗粒会像喷泉一样因重力而回落到环隙区表面而形成喷泉区。回落的颗粒沿环隙区缓慢向下移动至床层下部,然后又渗入喷射区被重新夹带上来而形成颗粒的极有规律的内循环。
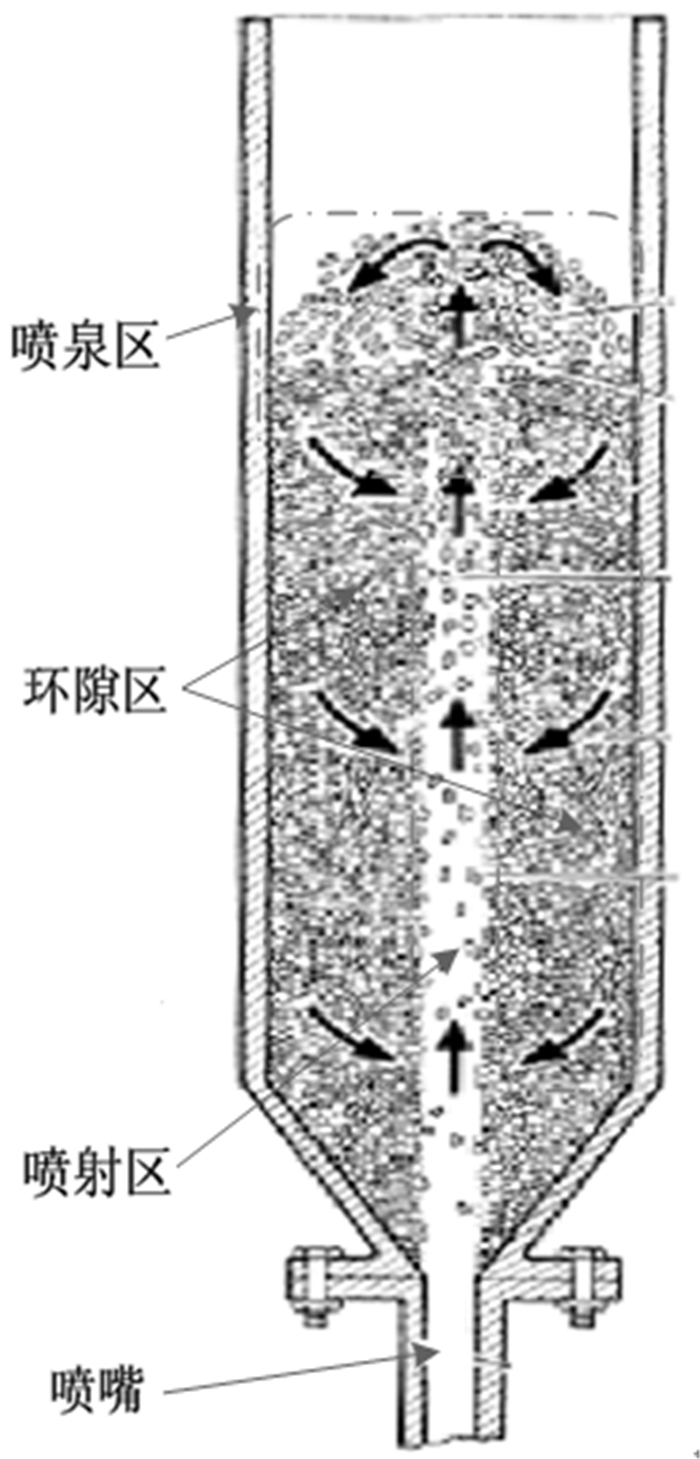 |
| 图 2 典型喷动床气固两相流 Fig.2 Typical gas-solid two-phase flow of spouted bed |
根据最小喷吹速度经验计算公式计算得到钛渣的最小喷吹速度分别为0.42、2.14、7.86和8.89 m/s,结合提出的数学模型以Fluent商业软件分别计算了在喷吹速度为1、2.14、7.86和8.89 m/s,床层反应时间为0.5 s时的钛渣喷动床床层内部气固两相流的流动特征,计算结果如图 3。
 |
| 图 3 不同最小喷吹速度下0.5 s时运动体积分数 Fig.3 Spouted fluidized bed of titanium slag Solids volume at Different minimum spouted velocity under 0.5 s |
根据图 3数值模拟结果可知,当表观气速在1 m/s和2.14 m/s时,此时气体是以渗流的方式通过固体床层,并未形成典型的喷动床流态化;当表观操作气速为7.86 m/s和8.89 m/s时,床层下部出现了一个明显的喷射区,然而也没有形成典型的喷动床流态化。但是表观气速8.89 m/s喷射区云图更加明显,因此数值模拟结果表明Gisher && Mathur[16]经验预测式更适合于本研究所选的钛渣颗粒。相关研究者在研究喷动床最小喷动速度时发现实际喷吹速度ums与理论计算的最小喷吹速度umf存在如式(8)的关系[16, 22]:
| $ {\frac{{{u_{ms}}}}{{{u_{mf}}}} = b = 0.9\sim1.5} $ | (8) |
以Gisher && Mathur[16]经验公式预测得到的最小喷吹速度结合式(8),选取b>1.1结合Gisher && Mathur[16]经验预测的最小流化速度分别选取喷吹速度为ums=10、11.5、13 m/s进行数值模拟。图 4是在三种喷吹速度下以0.2 s为一个时间间隔,反应时间段为0~0.5 s气固两相流的云图。
 |
| 图 4 不同表观气速下的喷动床固体颗粒体积分数 Fig.4 Spouted fluidized bed of titanium slag Solids volume at different superficial velocity a:表观气速为:10 m/s;b:表观气速为:11.5 m/s;c:表观气速为:13 m/s |
结合图 3和图 4(a)分析可知,在第0.3 s时,表观气速为8.89 m/s时床层内部还未出现明显的分区现象,当表观气速大于10 m/s时,三组图像均可以看出明显的喷动床三区分布(喷射区、喷泉区、环隙区),此时喷动床已经完全进入喷动床阶段,数值模拟结果表明,传统的最小流化速度计算公式并不能准确的预测最小喷吹速度,实际生产中如需准确控制最小喷吹速度需进一步结合式(8)并且使钛渣喷动床沸腾氯化b>1.1。
图 4中,三个不同的表观气速下喷动床内部颗粒已经进入稳定流化阶段,此时床内出现较为规律的三个分区。当表观气速为13 m/s时,床层钛渣颗粒在0.3 s左右到达顶部,吹透物料层后,喷泉区开始形成,达到最大喷吹高度。结合钛渣床层内部固体颗粒体积分数分析,随着表观气速增加,床层区域中稀相区占主体,并且倒锥形位置钛渣颗粒堆积程度明显少于其他表观气速,因此在实际操作过程中,为了适应高钙镁钛渣喷动床沸腾氯化工艺,减少床层颗粒黏结失流,应当尽量控制床层内部出现密相区,因此从图 4中可以看出表观操作气速越大越好,此时床层内部稀相区占主体,同时倒锥形位置钛渣堆积较少,黏结失流现象明显好于低速喷吹的情况。结合Gisher && Mathur[16]经验预测值和公式(8),要达到攀西地区钛渣喷动床沸腾氯化b≈1.4~1.5。
2.2.2 不同喷动速度下固体速度矢量图图 5给出了表观气速为13 m/s时床层内钛渣的速度矢量图。为了进一步比较不同表观气速下床层内部运行的稳定性,图 6分析了不同表观速度下床层内部不同区域的平均速度。
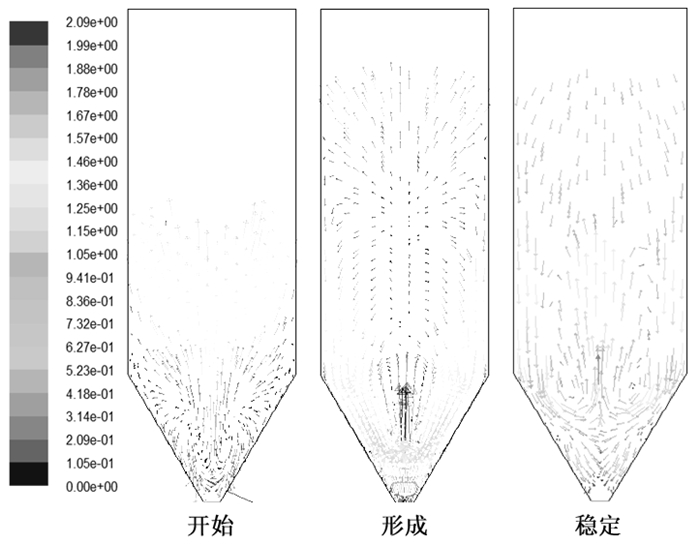 |
| 图 5 表观气速13 m/s时喷动床内钛渣速度矢量图 Fig.5 Spouted fluidized bed of titanium slag velocity vector at 13 m/s |
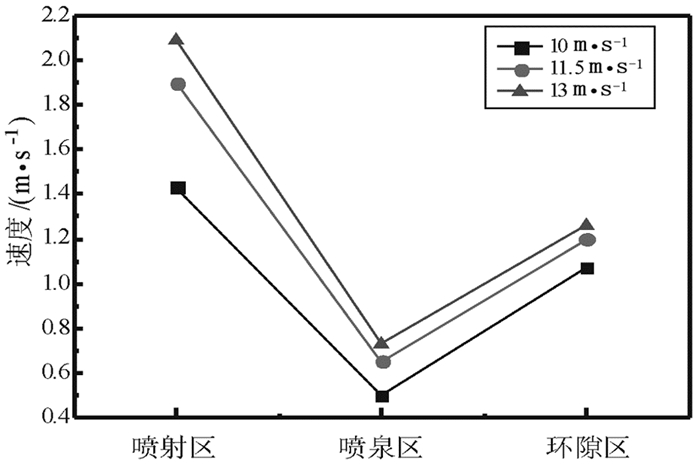 |
| 图 6 分区速度图 Fig.6 Speed curve of different regions |
从图 5喷动床床内气固两相流固相矢量图分析可知:床层的流动过程表现为三个阶段:开始、形成以及稳定阶段,当床层进入稳定阶段时床内三个分区较为明显。当表观气速为ums=13 m/s,数值模拟结果表明此时的喷动床分区较为明显,钛渣颗粒在喷动床内的运动轨迹已无太大变化,呈现出固有的流化规律,从喷动床开始到稳定阶段速度变化较大的是喷射区的钛渣颗粒速度,稳定时约为2.09 m/s,当床层达到稳定时内部速度分布较均匀,在环隙区形成高速区。
图 6结果表明:不同区域颗粒速度差异明显,最大速度均出现在喷射区,且喷射区的颗粒运动速度远大于环隙区和喷泉区,速度在轴向和径向上都有不同的分布规律。不同喷吹速度下相同区域的颗粒平均速度、最大运动速度也均有不同,呈现出随喷吹速度增加而增加的规律。
从图 7分析可知,喷嘴处的单个固体颗粒来看,钛渣颗粒沿中轴线垂直向上运动,先经过一个加速过程,达到最大速度,之后速度开始下降至零,此时颗粒达到最大高度,即喷动床的最大喷吹高度。颗粒达到最大高度后开始向四周运动进入环隙区,环隙区的颗粒主要靠近壁面运动,速度方向变为向下,速度小于喷射区的速度。速度较小时(ums=10 m/s),喷动床下部固体颗粒的运动并不非常规律,并没有呈现较为明显的对称分布,底部倒灌区域也不明显。但当速度大于11.5 m/s时,颗粒的运动就表现的十分规律,底部倒灌区域也变得明显,以喷动床中心为对称轴,在两侧呈对称分布。相关研究者[23, 24]采用数值模拟和实验研究二维喷动床床层内部气固两相流的流体动力学特征也得到了一致的颗粒运动特征轨迹。
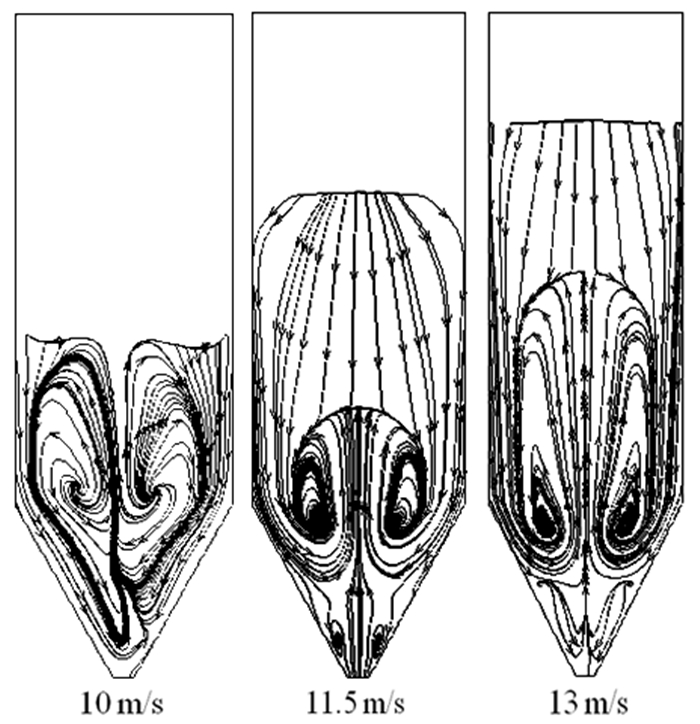 |
| 图 7 不同表观速度下的固体颗粒运动流线图 Fig.7 Spouted fluidized bed of titanium slag Solids Solid particle velocity streamline at different superficial velocity |
2.3 喷动床不同分区固体颗粒轨迹图分析
喷射区位于喷动床中轴线附近,是气体喷吹进行作用的主要区域,在这一区域速度梯度变化最大,固体颗粒在这个区域的运动最为剧烈,喷泉区是位于喷动床上部气固相呈喷泉状向四周分散的区域,环隙区位于靠近喷动床壁面的区域,固体颗粒在这一区域速度垂直向下,且速度变化不大,整体趋于稳定,图 8表示了不同表观气速下喷动床内固体颗粒进入稳定阶段时在不同分区的运动流线图。
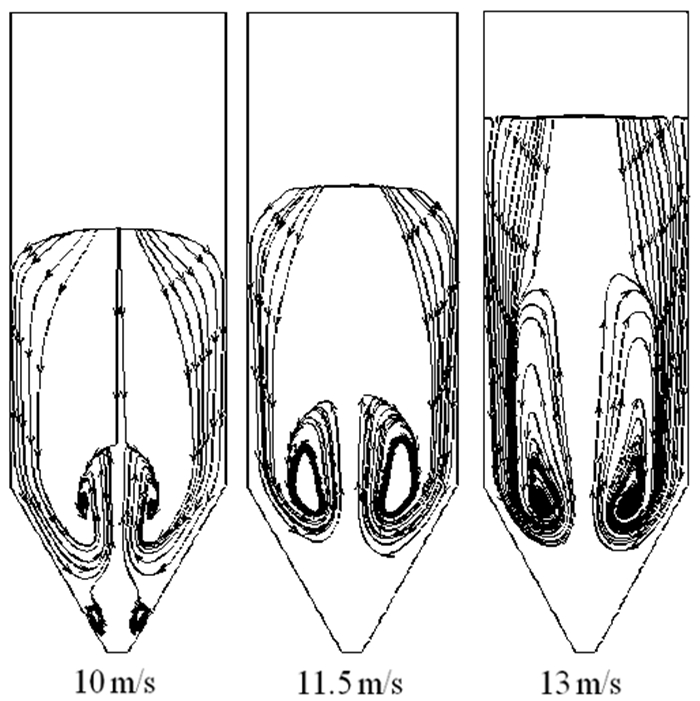 |
| 图 8 喷动床内固体颗粒分区运动图 Fig.8 Spouted bed of solid particles motion vector at different part |
喷射区的颗粒运动图可以在纵向上表现为底部喷嘴到顶部垂直速度为零这一区域,在横向上则根据不同的喷吹速度和倒锥角度的变化出现不同的宽度,倒锥型喷动床喷射区直径沿着轴向的变化如图 9所示,喷动床的直径、入口直径、颗粒尺寸等的不同,喷射区也会相应变化,通常有(a)、(b)、(c)、(d)四种类型,其中(a)型最普遍。结合图 7和图 8分析在本次数值模拟的三组图像中,ums=10 m/s时喷动床内固体颗粒运动不规则,没有出现明显的喷射区形状,但ums=11.5 m/s和13 m/s时均有明显的喷射区形状。其中ums=11.5 m/s时呈(b)型,ums=13 m/s时呈(a)型,说明在完全流化后,试验模拟所得喷射区的形状和理论形状较为吻合。
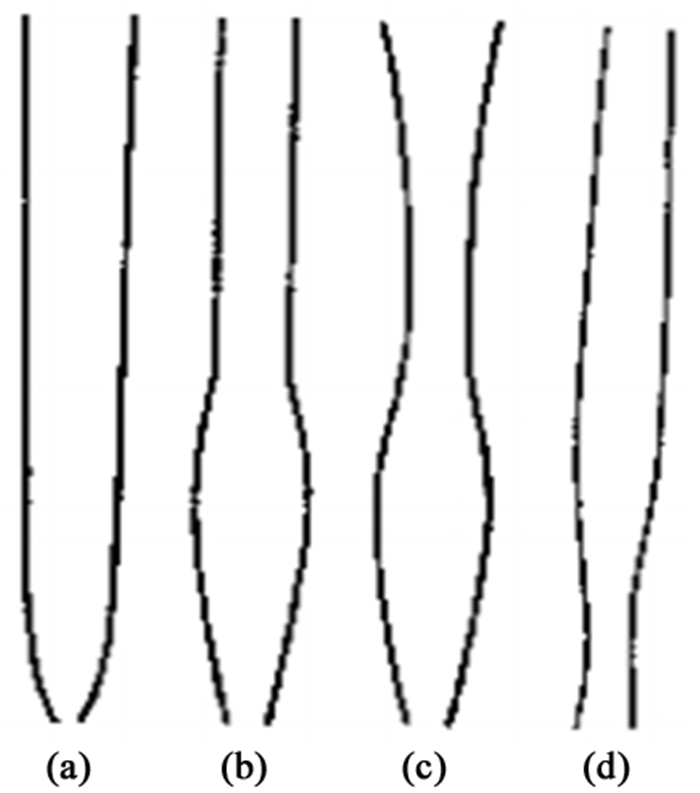 |
| 图 9 喷射区直径沿床层高度变化的4种形式[21] Fig.9 Spout diameter changes along the bed height |
钛渣喷动床沸腾氯化床层内的环隙区颗粒流线图如图 7所示。在环隙区内流体沿着竖直方向上表现为类似于移动填充床一样的弥散活塞流,而喷射区中流体流动在本质上是向上的活塞流。相关研究得到的环隙区流线如图 10所示。如果把图 8表示的环隙区内流体流线倒转,就基本上代表了环隙区内颗粒向下及向内的流线,结合图 8和图 10可以看出,表观气速为11.5 m/s和13 m/s时,环隙区内固体颗粒运动情况与文献结果相吻合[25]。
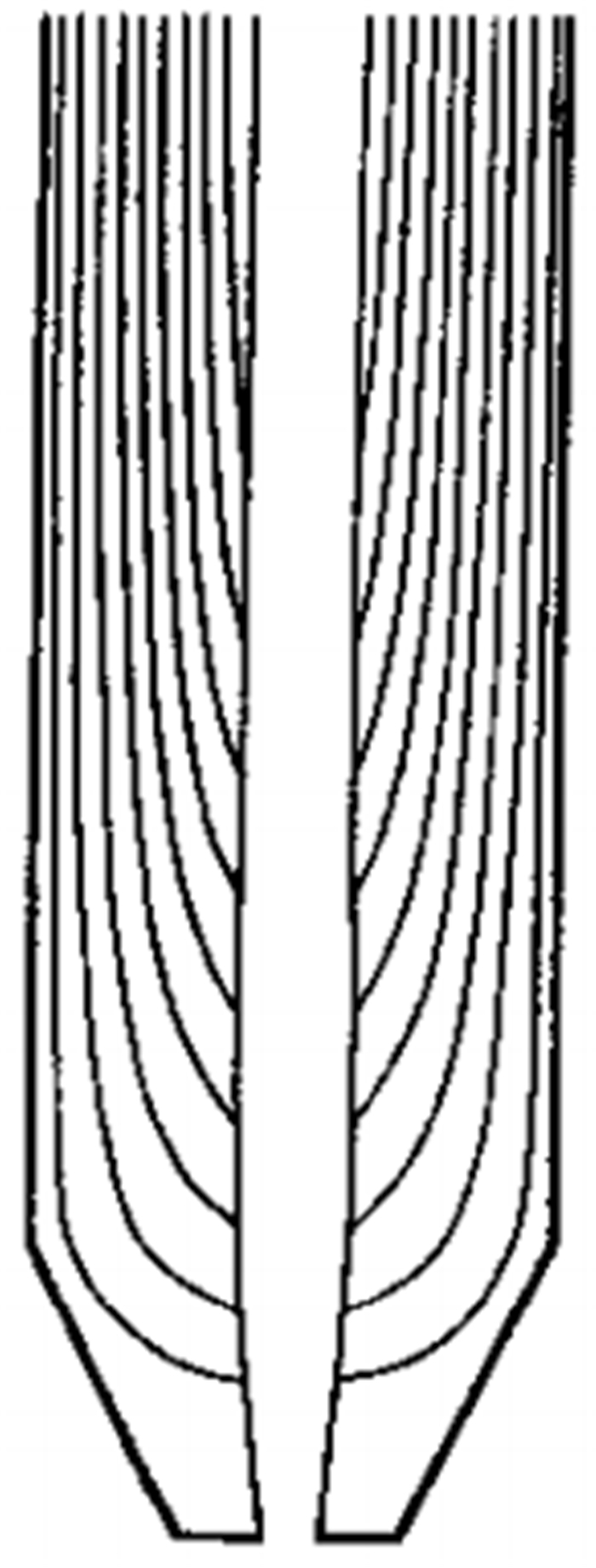 |
| 图 10 环隙区流线图[20] Fig.10 Streamlines of annulus |
图 8中可以明确看出,钛渣在不同表观气速下,喷泉区固体颗粒轨迹图在三个不同表观气速下钛渣达到最大喷吹高度时,固体颗粒分布稀疏,同时向壁面两边散开回落进入环稀区。Shuyan等[26]采用数值模拟结合试验研究气体和固体颗粒在床层内部的气固两相流特征,数值模拟和试验结果均清晰表明喷动床流态化过程存在三个分区,并且每个区的气固两相流的流动特征与本文数值模拟结果一致。
2.4 最大喷动高度数值模拟结果与讨论本研究数值模拟得到不同预测值在喷吹达到稳定阶段的最大喷吹高度结果如图 11所示。
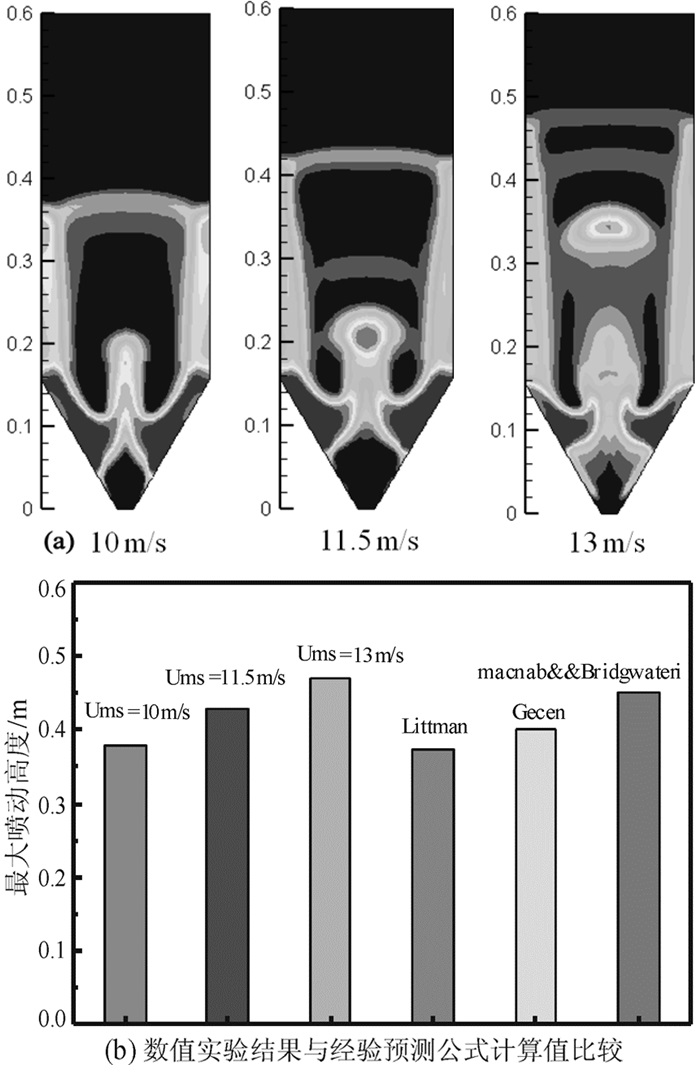 |
| 图 11 最大喷动床高图 Fig.11 maximum spoutable bed height |
图 11(a)为不同喷吹速度对应数值模拟得到床层的不同喷吹高度。结果表明:对应的最大喷吹高度约为0.38 m,ums=11.5 m/s对应的最大喷吹高度约为0.43 m,ums=13 m/s对应的最大喷吹高度约为0.47 m。不同喷吹速度下数值模拟得到的最大喷吹高度也不同,且最大喷吹高度与喷吹速度呈正相关,这与喷动床的流化特性是吻合的。
数值试验得到的最大喷吹高度与理论计算值对比结果如图 11(b)所示,在低操作气速(ums=10 m/s)时,数值模拟所得最大喷吹高度值(Hm=0.38 m)与Littman等[16]公式预测的最大喷动床高(Hm=0.373 m)较为吻合;在适宜攀枝花钛渣喷动床沸腾氯化的合理操作气速下(ums=13 m/s),数值模拟所得最大喷吹高度(Hm=0.47 m)均大于Cecen公式[21]预测的最大喷动床高(Hm=0.4 m)与McNab和Bridgwaterti[19]公式预测的最大喷吹高度(Hm=0.45 m),两者误差分别为:14.89%和4.26%;因此McNab和Bridgwaterti[19]公式更适合预测攀枝花钛渣喷动床沸腾氯化床层的最大喷吹高度。同时利用该公式计算的最大喷吹高度更能为实际生产过程中反应器设计方面提供指导。
3 结论(1) 本文建立了一个钛渣喷动床沸腾氯化气固两相流的预测模型。模型方程包括了:双流体模型、钛渣最小喷吹速度经验公式以及气固相间耦合机制。
(2) 模型求解结合攀枝花钛渣物性,以压力基隐式非稳态方式求解,模型方程采用Simple算法离散、黏性模型选择。在壁面处,气-固两相流使用无滑移边界条件,体积分数差分格式采用QUICK格式的,该数学模型能够准确的模拟钛渣喷动床沸腾氯化气固两相流流动特征。
(3) 数值模拟结果表明:Gisher && Mathur公式结合修正公式(8)且式中b≈1.4~1.5适合攀西地区钛渣喷动床沸腾氯化最小喷吹速度的预测。
(4) 最小喷吹速度13m/s能够准确的预测攀西地区钛渣喷动床沸腾氯化床层内部三个分区的流动特征,且模拟结果与相关研究研究具有一致性。更重要的是最小喷吹速度为13m/s时,床层中固体料层速度和床层内部钛渣分布较为均匀,倒锥位置固体料层堆积较少,能够避免实际操作过程中因钙镁含量过高导致床层黏结失流。
(5) 在适宜攀枝花钛渣喷动床沸腾氯化的最小喷吹速度ums=13 m/s下进行数值模拟得到的最大喷吹高度与McNab和Bridgwaterti公式预测值误差为4.26%。因此McNab和Bridgwaterti公式更适合于预测攀枝花钛渣喷动床沸腾氯化的最大喷吹高度。
| [1] |
刘禹明, 王伟, 钱鑫. 大型无筛板沸腾氯化技术及装备的研发与应用[J]. 钛工业进展, 2014(1): 35-37. |
| [2] |
杨平, 陈德明. 攀枝花钛渣组合式流化床氯化制备TiCl4的研究[J]. 钢铁钒钛, 2007, 28(2): 48-52. DOI:10.7513/j.issn.1004-7638.2007.02.010 |
| [3] |
马崇振. 攀枝花某铁尾矿提钛降杂试验研究[J]. 矿产保护与利用, 2016(5): 74-78. |
| [4] |
成文江. 人造金红石加入量对沸腾氯化工艺的影响[J]. 中国有色金属, 2006(12): 68-69. |
| [5] |
牛丽萍, 张延安, 吕国志, 等. 天然金红石粉体沸腾氯化工艺条件优化研究[J]. 过程工程学报, 2011, 11(6): 1002-1009. |
| [6] |
金涌. 流态化工程原理[M]. 北京: 清华大学出版社, 2002.
|
| [7] |
Rüdisüli M, Schildhauer T J, Biollaz S M A, et al. Bubble characterization in a fluidized bed by means of optical probes[J]. International Journal of Multiphase Flow, 2012, 41(2): 56-67. |
| [8] |
Yuan P T, Gidaspow D. Computation of flow patterns in circulating fluidized beds[J]. Aiche Journal, 1990, 36(6): 885-896. DOI:10.1002/(ISSN)1547-5905 |
| [9] |
Felice R D. The voidage function for fluid-particle interaction systems[J]. International Journal of Multiphase Flow, 1994, 20(1): 153-159. DOI:10.1016/0301-9322(94)90011-6 |
| [10] |
Wen C Y, Yu Y H. Mechanics of fluidization[J]. Chem. Engng Prog. Symp. Ser, 1966, 62: 100-111. |
| [11] |
Ergun S. Fluid flow through packed columns[J]. Chem. Eng. Prog, 1952, 48(2): 89-94. |
| [12] |
And D L K, Hill R J. Inertial effects in suspension and porous-media flows[J]. Annual Review of Fluid Mechanics, 2003, 33(1): 619-647. |
| [13] |
Beetstra R, Vander Hoef M, Kuipers J. Numerical study of segregation using a new drag force correlation for polydisperse systems derived from lattice-Boltzmann simulations[J]. Chemical Engineering Science, 2007, 62(1): 246-255. |
| [14] |
Gidaspow D. Multiphase Flow and Fluidization[J]. Multiphase Flow & Fluidization, 1994(95): 1-29. |
| [15] |
Zheng Z, Lin L, Chen Z. A dual-scale lattice gas automata model for gas-solid two-phase flow in bubbling fluidized beds[J]. Computers & Mathematics with Applications, 2011, 61(12): 3593-3605. |
| [16] |
Li T, Gopalakrishnana P, Garg R, et al. CFD-DEM study of effect of bed thickness for bubbling fluidized beds[J]. Particuology, 2012, 10(5): 532-541. DOI:10.1016/j.partic.2012.02.006 |
| [17] |
Goldschmidt M J V, Kuipers J A M, Swaaij W P M V. Hydrodynamic modelling of dense gas-fluidised beds using the kinetic theory of granular flow: effect of coefficient of restitution on bed dynamics[J]. Chemical Engineering Science, 2001, 56(2): 571-578. DOI:10.1016/S0009-2509(00)00262-1 |
| [18] |
Fane A G, Mitchell R A. Minimum spouting velocity of scaled-up beds[J]. Canadian Journal of Chemical Engineering, 2010, 62(3): 437-439. |
| [19] |
Mcnab G S, Bridgwater J. A theory for effective solid stresses in the annulus of a spouted bed[J]. Canadian Journal of Chemical Engineering, 1979, 57(3): 274-279. |
| [20] |
Iii M H M, Littman H. Predicting the maximum spoutable height in spouted beds of irregularly shaped particles[J]. Industrial & Engineering Chemistry Fundamentals, 1982, 21(1): 23-26. |
| [21] |
Çeçen A. The maximum spoutable bed heights of fine particles spouted with air[J]. Canadian Journal of Chemical Engineering, 2010, 72(5): 792-797. |
| [22] |
Ye B, Lim C J , Grace J R . Hydrodynamics of spouted and spout-fluidized beds at high temperature[J]. Canadian Journal of Chemical Engineering, 1992, 70(5): 840-847. DOI:10.1002/cjce.v70:5 |
| [23] |
Hosseini S H, Fattahi M, Ahmadi G. Hydrodynamics studies of a pseudo 2D rectangular spouted bed by CFD[J]. Powder Technology, 2015, 27(9): 301-309. |
| [24] |
Hosseini S H , Ahmadi G, Olazar M. CFD study of particle velocity profiles inside a draft tube in a cylindrical spouted bed with conical base[J]. Taiwan Inst. Chem.Eng, 2014, 45: 2140-2149. DOI:10.1016/j.jtice.2014.05.027 |
| [25] |
Mathur K B, Epstein N. Developments in spouted bed technology[J]. Canadian Journal of Chemical Engineering, 1974, 52(2): 129-144. DOI:10.1002/cjce.v52:2 |
| [26] |
Shuyan Wang, Baoli Shao, Rui Liu, et al. Comparison of numerical simulations and experiments in conical gas-solid spouted bed[J]. Chinese Journal of Chemical Engineering, 2015, 23(10): 1579-1586. DOI:10.1016/j.cjche.2015.07.006 |
 2017
2017 
