| 基于CFD-DPM模型的浮选机内固相颗粒行动行为研究 |
2. 广西大学 资源环境与材料学院,广西 南宁 530004
2. School of Resources, Environment and Materials, Guangxi University, Nanning 530004, China
不同矿石颗粒表面的物理、化学性质有所不同,浮选就是通过这种差异将有用矿物从脉石矿物中分离开来[1-4]。浮选机作为浮选的核心设备,其流场设计和所选型号的合理性会很大程度地影响浮选指标和浮选效率。影响浮选机指标的关键因素又集中体现在浮选机内所形成的气-液-固三相流场的特性[5-7]。合理的流场分布有利于分选效率、精矿品位等的提高,大大地减少能耗,并提高选矿厂的经济效益[8],所以浮选机内的流场一直都是业内研究热点。
浮选过程中,气泡和矿物颗粒需要在槽内均匀弥散,从而固体颗粒不至于在槽内沉积,保证颗粒与气泡的碰撞矿化正常进行。因此,为满足气泡和固体颗粒的运动及分布,浮选机要提供与之相适应的流场,进而提高浮选指标[9-10]。由于转子与定子相对运动及相互作用,槽内流场呈现出复杂的周期性三维非稳态湍流特性[11],其过程常常涉及到多相体系,分散相的引入进一步加剧其流动的复杂性[12, 13]。因而对浮选机内流体动力学特性的认识对设计、放大、优化和调控来说具有重大意义[14-16]。在国外,澳大利亚联邦科学院Peter Kohn等[17]对浮选机流场方面做了大量的研究工作,主要采用欧拉-欧拉模型,并将气相当做拟流体来研究浮选机的内部气-液两相流场。而我国北京矿冶科技集团有限公司的沈政昌等[18, 19]对浮选机的流体动力学参数进行深入研究,从流场流态、循环能力大小两方面来优化其浮选机的关键构造。通过对浮选机多相流体动力学特性的研究将浮选机的实际工作参数、动力学参数和浮选性能之间合理地联系起来,并综合了工业试验和理论研究的优点,大大减少了其研发的成本[20-22]。本文以KYF-0.2浮选机为研究对象,采用CFD-DPM离散模型对浮选机内的固相颗粒行动行为进行了CFD模拟研究[23-25],有利于揭示固体颗粒在槽体内分散及运动轨迹。
1 浮选机模型及数值模拟 1.1 浮选结构由北京矿冶科技集团制作的KYF-0.2充气机械搅拌式浮选机结构示意图如图 1所示,其槽体规格是Φ720 mm×640 mm,单槽容积0.2 m3。叶轮后倾,特殊的空气分配器结构,配合流动阻力低的定子形成了浮选机的搅拌系统,如图 2所示。叶轮和定子的直径分别为240 mm和390 mm。
 |
| 图 1 KYF-0.2充气式机械搅拌式浮选机 Fig.1 KYF-0.2 type inflatable mechanical flotation machine |
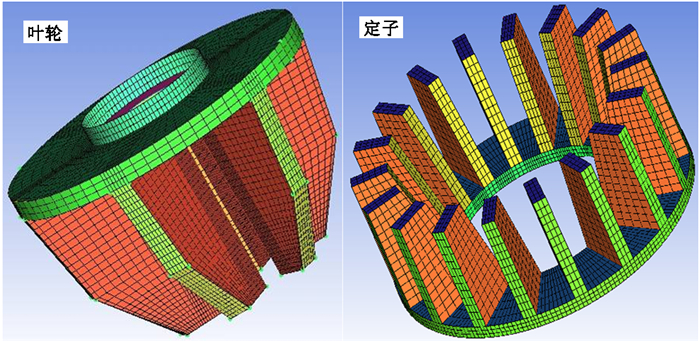 |
| 图 2 浮选机叶轮和定子 Fig.2 Impeller and stator in flotation machine |
1.2 浮选机网格化处理
在PRO-E软件中对KYF-0.2充气机械搅拌式浮选机几何模型进行建模。网格化工具采用ICEM-CFD软件,可以实现很好的结构化网格处理。为实现浮选机叶轮搅拌气液两相流的模拟,叶轮的旋转建立在运动坐标系下,而定子和槽体等静止部件则在建立在静止坐标系下,即采用多重参考坐标系方法解决浮选机叶轮的旋转问题。
图 3~图 5为叶轮旋转域和定子槽体区域。综合考虑结构网格给计算带来的优势,采用六面体结构化网格对整个浮选机进行网格化处理。
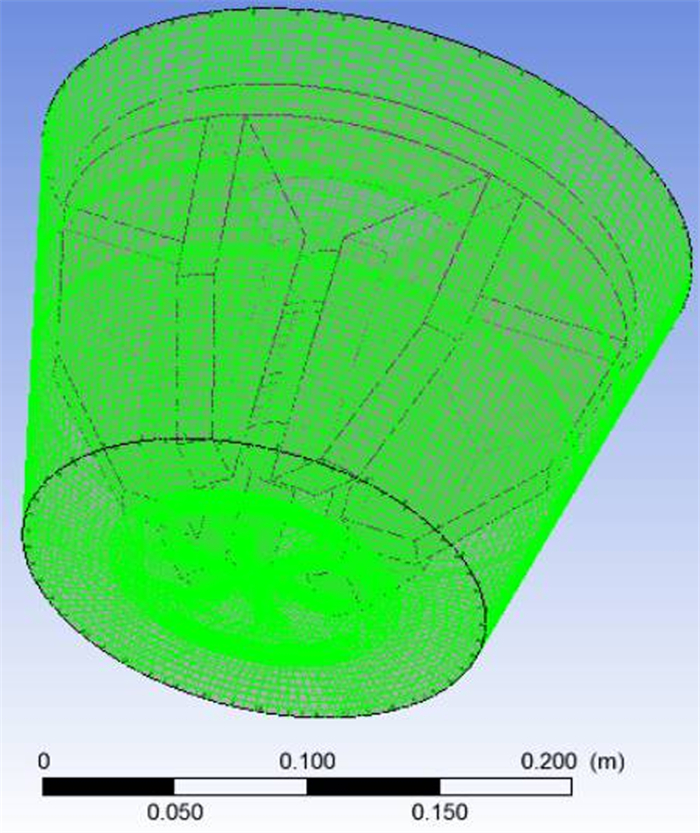 |
| 图 3 旋转区域 Fig.3 Rotating region |
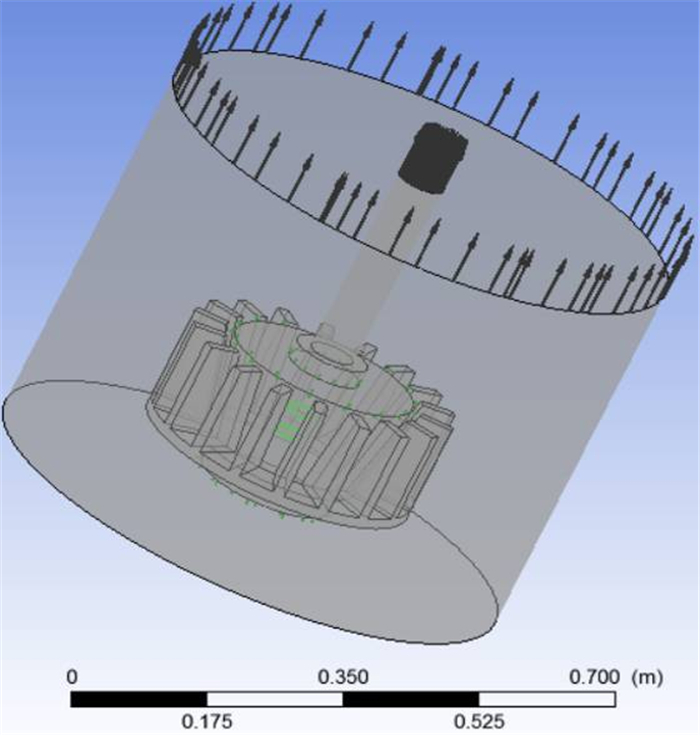 |
| 图 4 定子槽体区域 Fig.4 The tank area of stator |
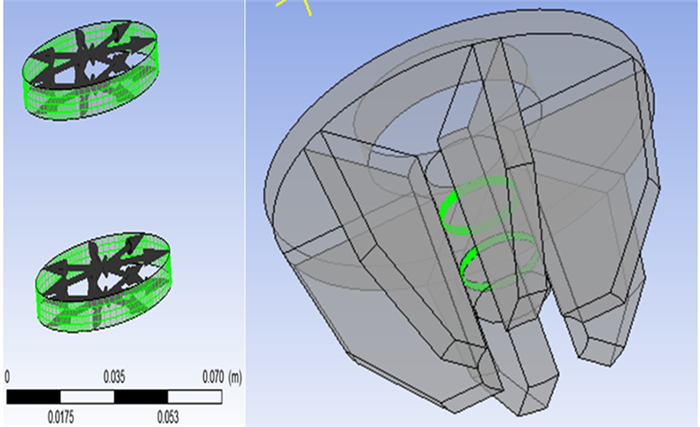 |
| 图 5 环形空气分配器 Fig.5 Annular air distributor |
网格数量对计算精度的影响是数值仿真研究的重要方面。网格数量少,可以提高计算速度,但精度低。网格数量过多的话,计算时间过长,而计算精度的提高也十分有限。为此通过网格敏感性分析来综合考虑计算结果的准确性和经济性,确定最终仿真所使用网格得数量,分析结果如表 1所示。
| 表 1 浮选机各区域网格数量 Table 1 Grid number of flotation machine |
 |
1.3 计算参数
本文选用标准k-ε湍流模型,选用欧拉-拉格朗日方法处理多相流。浮选机的叶轮定子结构采用稳态的多重参考坐标系法(MRF)和瞬态的滑移网格法(SG)。固液两相流模拟中,固体颗粒设置为石英颗粒,摩尔质量为60 g/mol,密度为2.2 g/cm3,ω(石英)=29%,比热容为966 J/(kg·K),为简化模拟过程,我们假设固体颗粒粒径统一为0.074 mm。转子区域转速为315 r/min。固液两相相间作用力考虑曳力、升力、湍流扩散力、湍流传输力的影响。湍流分散力模型采用默认的Lopez de Bertodano模型,分散系数设置为0.1。湍流传输力模型则考虑采用Sato Enhanced Eddy Vicosity模型。其他相间力如虚拟质量力等,由于其作用大多微小,这里暂时不予考虑。同时开启浮力作用,参考密度设为水的密度,浮力参考坐标设为浮选槽的顶面。先进行稳态计算,再进行瞬态模拟。
2 结果讨论与分析在欧拉-拉格朗日多相流模型下有两种方法,完全耦合和单向耦合。完全耦合可以揭示颗粒和流场之间耦合作用;单向耦合应用最广,但仅能反映流场对颗粒的影响。固体颗粒数在单向耦合和双向耦合中分别设置为5 000和200。双向耦合耗费资源较大,计算时间长,需要的数值运算更为复杂,所以,双向耦合的设置颗粒数量少一些。相间作用力设置方面,曳力模型选取Schiller Naumann,最大跟踪时间定为180 s。
2.1 单向耦合颗粒图 6给出了欧拉-拉格朗日模型下,单向耦合作用时固体颗粒的颗粒运动轨迹图。
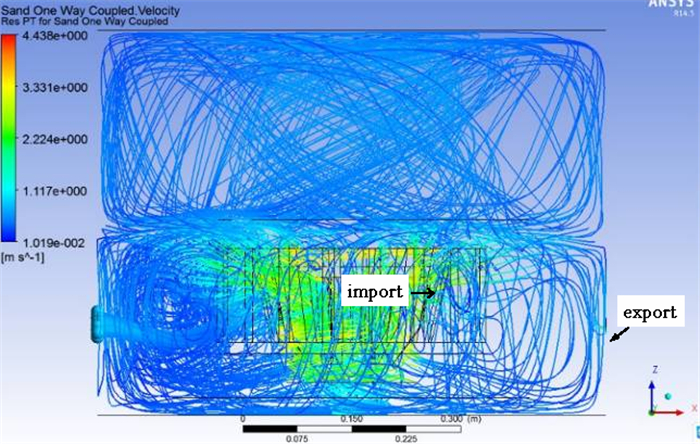 |
| 图 6 固体颗粒的运动轨迹(单向耦合条件下) Fig.6 The trajectory of solid particles under one way coupling condition |
图 7是通过CFD的后处理,随机挑选50个颗粒的运动轨迹图,固体颗粒速度的大小用轨迹线的颜色表示(如图中左边标尺所示)。
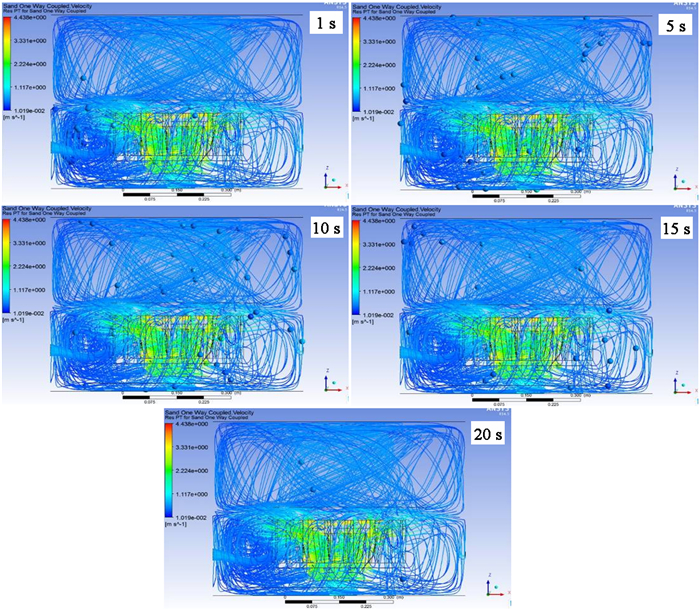 |
| 图 7 不同时刻下固体颗粒的运动轨迹 Fig.7 The trajectory of the solid particles at different time |
固体颗粒刚进入如图所示的左边进口,此时颗粒跟踪时间为0。进一步截取了5个不同时刻,揭示固体颗粒在浮选槽内的位置。从图 7可以看出,在第1 s时,固体颗粒在浮选机的入口进入,由于叶轮的搅拌混合作用,从5~15 s的时间内,排出的颗粒一部分被循环到下部流场区域,另一部分在则向上流动到上部流场区。大约20 s的时间里,固体颗粒已很少在浮选机槽体内,大部分颗粒已经从出口流出浮选机。不难发现,仅选取50个固体颗粒来说明矿物在浮选机的停留时间分布特性是不完善。因此,图 8则揭示了不同颗粒数条件下,单向耦合分析中颗粒的跟踪时间。
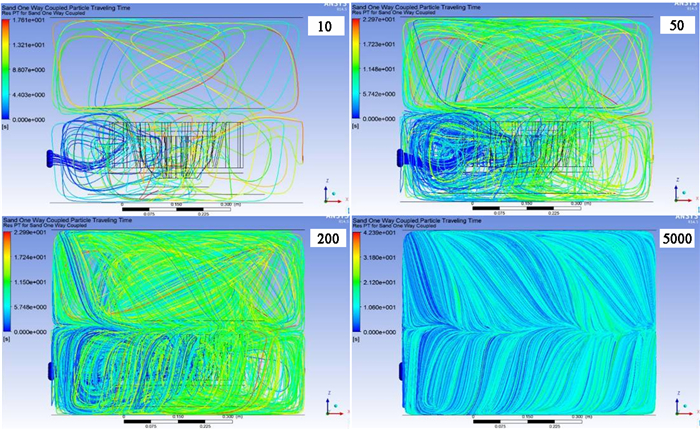 |
| 图 8 不同固体颗粒数时的跟踪时间 Fig.8 The tracking time with different number of solid particles |
如图 8中所示,跟踪时间的大小如图中左边后处理软件自动生成的标尺所示。云图中的曲线表示的是颗粒的运动路径。在后处理中,跟踪时间与颗粒的数量相关。可以看到,颗粒数为10时,最大跟踪时间仅为18 s。若颗粒数提高到50时,最大跟踪时间变为23 s。若5 000颗粒均进行处理时,最大跟踪时间达到了42 s。浮选过程中的矿物颗粒的粒子数是非常多,本例所模拟的5 000个固体颗粒还不足以完全反应浮选机的实际运行情况。所以,揭示的最大粒子跟踪时间与理想的浮选设备内矿物颗粒的实际停留时间是有差异的。
2.2 完全耦合颗粒欧拉-拉格朗日模型下,选取50个固体颗粒进行追踪,双向耦合作用时固体颗粒的颗粒运动轨迹图如图 9所示。
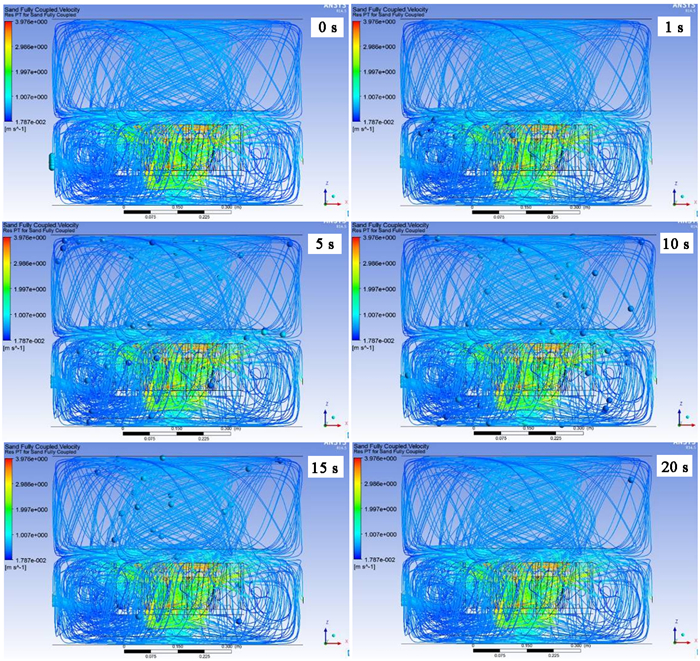 |
| 图 9 不同时刻下固体颗粒的位置 Fig.9 The location of the solid particles at different time |
通过与单向耦合条件下的颗粒运动轨迹线进行比较,完全耦合条件下没有出现显著的差异性。从颗粒的速度看,单向耦合条件时,运动速度稍大。
图 10反映的是200个固体颗粒在完全耦合作用下的跟踪时间分布云图。可以得到,200个颗粒在完全耦合条件下的跟踪时间达到26 s,略大于单向耦合作用下23 s的最大的跟踪时间。流线的颜色表征速度的大小,分析图 10可知,完全耦合条件下,固体颗粒的运动速度较单相耦合条件下的要小,流场结构影响了固体颗粒的运动,同时也说明了固体颗粒在浮选槽内的停留时间在完全耦合作用下要大一些。
 |
| 图 10 200个颗粒跟踪时间 Fig.10 The tracking time of 200 solid particles |
3 结论
研究浮选机性能主要是研究浮选机矿物颗粒的流动特性。针对一些流场特性与颗粒的运动轨迹的研究,并不能靠传统的试验技术获取。本文采用欧拉-拉格朗日方法针对浮选机内颗粒的运行特性进行单向耦合和双向耦合的研究。数值模拟结果很好的揭示了矿物颗粒在浮选机内的流动轨迹,为优化浮选设备流体动力学性能做进一步的研究奠定了基础。
| [1] |
王淀佐, 邱冠周, 胡岳华. 资源加工学[M]. 北京: 科学出版社, 2005.
|
| [2] |
印万忠, 孙传尧. 硅酸盐矿物浮选原理研究现状[J]. 矿产保护与利用, 2001(3): 17-22. |
| [3] |
朱建光. 浮选药剂的进展[J]. 国外金属矿选矿, 1998(3): 14-22. |
| [4] |
沈政昌. 浮选机理论与技术[M]. 北京: 冶金工业出版社, 2012.
|
| [5] |
沈政昌. 柱浮选技术[M]. 北京: 冶金工业出版社, 2015.
|
| [6] |
沈政昌, 樊学赛, 杨丽君, 等. 单槽容积600 m3充气机械搅拌式浮选机流场研究[J]. 有色金属(选矿部分), 2013(S1): 195-198. |
| [7] |
王昌安. 国外充气机械搅拌式浮选机研究与进展[J]. 矿业快报, 2005, 17(3): 9-13. |
| [8] |
沈政昌, 陈建华. 浮选机流场模拟及其应用[M]. 北京: 科学出版社, 2012.
|
| [9] |
沈政昌, 刘惠林, 刘承帅. 国内外大型浮选机的应用与进展[J]. 金属矿山, 2010(8). |
| [10] |
赵昱东. 浮选机的应用与发展[J]. 矿山机械, 2007, 35(7): 65-68. |
| [11] |
白丽梅, 刘忠义, 韩跃新, 等. 浮选动力学模型的应用与发展[J]. 矿产保护与利用, 2016(4): 56-63. |
| [12] |
张晋霞, 牛福生, 王学涛. KYF型浮选机单-液相流体特性模拟研究[J]. 矿产保护与利用, 2017(2): 62-68. |
| [13] |
杨应江, 陈建华, 沈政昌, 等. 充气搅拌式浮选机流场特性模拟研究[J]. 矿产保护与利用, 2015(2): 22-26. |
| [14] |
唐堃. 大型机械搅拌充气式浮选机内部流场的数值模拟[D]. 兰州: 兰州理工大学, 2009.
|
| [15] |
韩伟. 浮选机内多相流动特性及浮选动力学性能的数值研究[D]. 兰州: 兰州理工大学, 2009.
|
| [16] |
胡明振, 陈锦全, 吴伯增, 等. 大型贫锡硫化矿浮选机内流场特性的数值模拟[J]. 矿业研究与开发, 2014(7): 71-74. |
| [17] |
Koh P T L, Schwarz M P. CFD model of a self-aerating flotation cell[J]. International Journal of Mineral Processing, 2007, 85(1-3): 6-24. |
| [18] |
沈政昌, 卢世杰, 史帅星, 等. KYF型浮选机三相流仿真研究初探-KYF浮选机流场测试与仿真研究(六)[J]. 有色金属(选矿部分), 2013(6): 67-72. |
| [19] |
沈政昌, 卢世杰, 史帅星, 等. 基于CFD的KYF浮选机气-液两相流分析与探讨-KYF浮选机流场测试与仿真研究(四)[J]. 有色金属(选矿部分), 2013(4): 59-63. |
| [20] |
王学涛. 矿物浮选过程中的三相流体特征研究[D]. 北京: 华北理工大学, 2016.
|
| [21] |
韩伟, 李仁年, 杨瑞, 等. 基于内流场分析的机械搅拌式浮选机改型设计[J]. 机械工程学报, 2009(12): 84-88. |
| [22] |
徐振法, 韩伟. 机械搅拌式浮选机的流体动力学分析[J]. 煤矿机电, 2009(3): 51-52. |
| [23] |
肖志锋, 乐建波, 吴南星. 基于CFD-DPM的陶瓷料浆喷雾干燥过程数值模拟[J]. 硅酸盐通报, 2014, 33(9): 2186-2190. |
| [24] |
李良超, 徐斌, 向科峰. 双层桨搅拌槽内气液分散特性的CFD-DPM模拟[J]. 排灌机械工程学报, 2013, 31(2): 151-156. |
| [25] |
曹亮, 陈东, 张文明, 等. 一种粗颗粒机械搅拌式浮选机的研究[J]. 有色金属(选矿部分), 2007(4): 26-28. |
 2018
2018 


