| 菱锌矿晶体各向异性与表面性质研究 |
2. 东北大学 资源与土木工程学院, 辽宁 沈阳 110819
2. School of Resources and Civil Engineering, Northeastern University, Shenyang 110819, China
同一矿物不同晶面的活性质点分布、断裂键和表面能存在差异,也就是晶体表面的各向异性。晶体各向异性决定了矿物碎磨时一般平行于面网密度最大、电性中和面网、同号离子组成的相邻面网以及较强化学键连接的面网方向有规律解理[1]。为定性描述矿物解理规律,研究者提出了米勒指数、断裂键密度和表面能等定量参数[2, 3],其中,断裂键密度和表面能有良好的对应关系,前者与晶体化学的配位关系、键型和晶胞参数等相关,更为直观,后者主要依赖于计算机模拟。两者相结合不仅可相互验证计算结果合理性,而且可深入分析矿物晶体化学性质、表面元素种类及其化学活性。
计算机模拟为分子层次认识浮选药剂作用机理提供了条件,分子模拟结果可靠性不仅与计算过程相关,也取决于模型选取的合理性。例如,油酸钠与白钨矿和方解石不同晶面作用的强弱顺序为白钨矿(001)面 < 方解石(104)面<方解石(018)面<白钨矿(112)面[4],说明不同矿物与药剂作用能力强弱顺序与表面结构模型选取密切相关,否则得出与实践矛盾的结论。此外,有研究得出磷灰石(001)面存在三种不同断面的表面结构模型,三种模型表面原子种类和空间排布方式存在明显差异[5],必然导致药剂吸附机制差异。
菱锌矿是一种典型的氧化锌矿物,是锌的重要来源之一。矿石中的菱锌矿主要应用浮选法实现回收,包括硫化—黄药浮选法、硫化—胺浮选法、脂肪酸浮选法、螯合剂浮选法和絮凝浮选法等,其中前两种是最常用的方法[6]。药剂是实现菱锌矿浮选的前提,为更好了解菱锌矿表面与药剂作用机制,研究者应用密度泛函理论(DFT)从分子层次上分析了菱锌矿的晶体化学特征、表面结构[7],以及硫化钠组分、捕收剂与菱锌矿作用机制。归纳发现,不同研究者在选取菱锌矿表面结构模型存在差异,例如,Liu、王瑜以菱锌矿(001)面研究硫化钠组分的作用机制[8, 9],Chen、Liu、Cui、Zhao和Han等以菱锌矿(101)面研究菱锌矿浮选机制[10-14]。矿物晶体各向异性决定了不同结晶方向表面的原子空间位置、断裂键性质和活性等存在差异,进而影响分子模拟与试验结果的吻合程度,因此有必要分析菱锌矿解理规律,从理论上确定菱锌矿常见解理面,为后续分子模拟和预测浮选特性提供依据。
1 计算模型及方法菱锌矿(ZnCO3)属于岛状碳酸盐矿物,三方晶系,方解石型结构,空间群为:菱面体晶胞参数a=5.84 Å,α=47°46’,六方晶胞参数a=b=4.73 Å,c=15.49 Å,α=β=90°, γ=120°。计算模拟采用Materials Studio 2017软件中的Castep模块进行,采用的方法是密度泛函理论框架下的第一性原理。根据文献报道,计算采用广义梯度近似(GGA)下的WC和PBE交换相关泛函[8, 14],采用BFGS算法,自恰迭代收敛精度SCF设为2×10-6 eV/atom,k点取样密度为3×3×2,截断能取300 eV。为更全面分析断裂键密度与表面能关系,采用GCA/WC优化菱锌矿晶胞,几何优化的收敛参数设置为:原子间相互作用力不大于0.05 eV/atom,晶体内应力不大于0.1 GPa,原子最大位移不大于2×10-4 nm,迭代次数不超过100次。作为对比,采用GCA/PBE计算未经优化的菱锌矿晶格能和表面能。菱锌矿切割层数为3,真空层厚度为1.5 nm,该条件下表面能随切割层厚度的增加变化不大,且有效消除上下两底面间相互干扰。
晶面的表面能(Esurf)和断裂键密度的计算公式分别如式(1)和(2)所示:
| $ {E_{{\rm{surf}}}} = \frac{{{E_{{\rm{slab}}}} - \left( {{N_{{\rm{slab}}}}/{N_{{\rm{bulk}}}}} \right){E_{{\rm{bulk}}}}}}{{2A}} $ | (1) |
| $ {D_b} = \frac{{{N_b}}}{A} $ | (2) |
Eslab和Ebulk分别为解理面结构模型和原胞的能量, J;Nslab和Nbulk分别为解理面结构模型和原胞的所包含的原子数目;Db为晶面上单位面积的断裂键数目;Nb为晶面范围内断裂键数目;A为计算表面的面积,m2或nm2;
2 结果与讨论 2.1 菱锌矿晶体结构与化学键分析如图 1所示,Zn与周围的6个CO32-中的O成6配位,C与O结合成3配位,O与周围的2个Zn和1个C结合成3配位。图 2为菱锌矿的X射线粉晶衍射图,衍射峰与晶面指数的对应关系如图 2所示,由此可推测,菱锌矿可能沿平行于(012)、(104)、(110)、(113)、(101)、(214)、(300)等晶面发生解理。
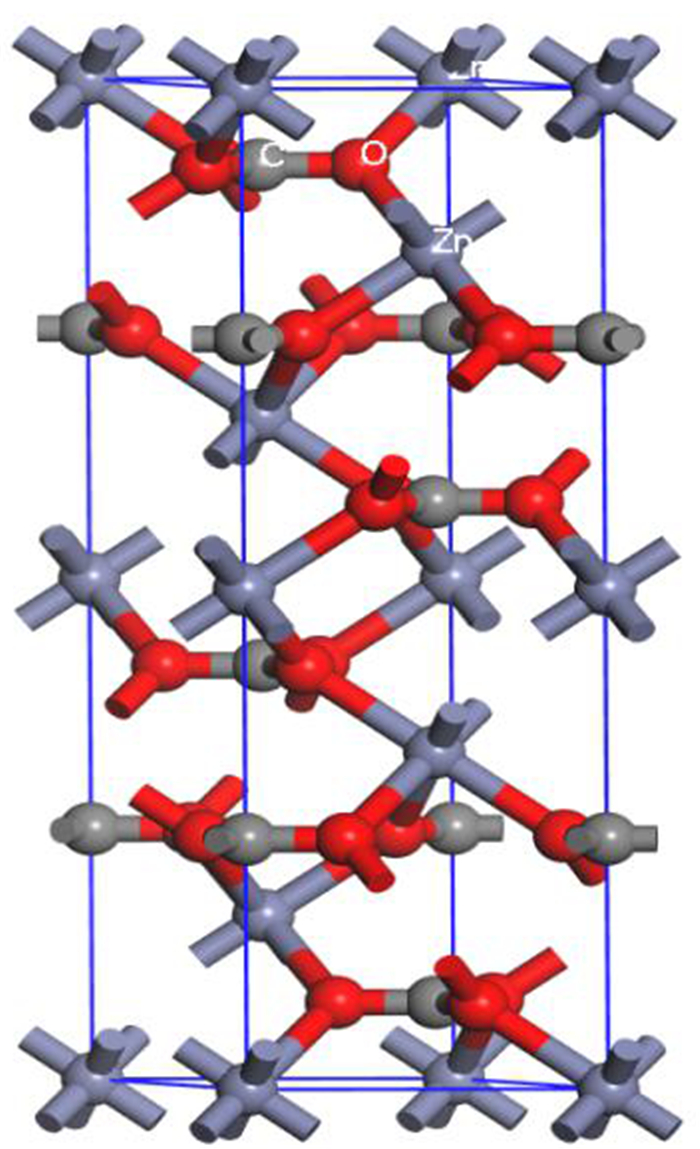 |
| 图 1 菱锌矿晶体结构 Fig.1 Crystal structure of smithsonite |
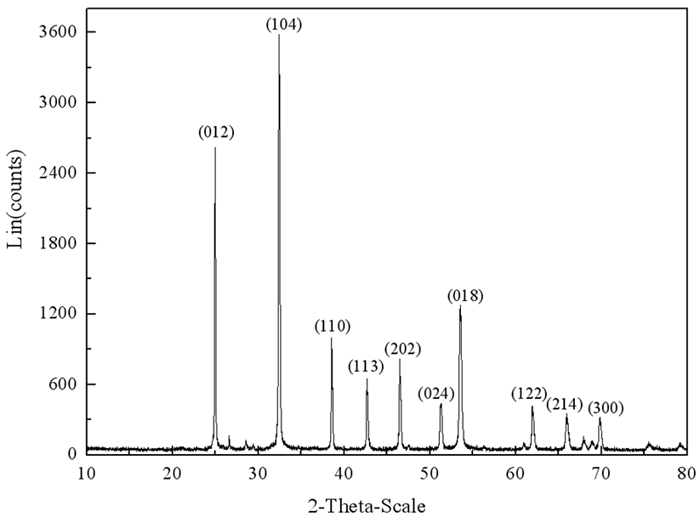 |
| 图 2 菱锌矿X射线粉晶衍射图 Fig.2 XRD pattern of smithsonite |
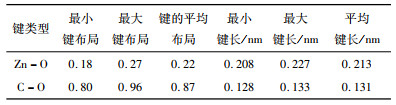
表 1为菱锌矿Mulliken键布局计算结果。键的Mulliken布局数分析显示相邻原子之间电子云重叠度,其值越大则化学键的共价性越强,反之,键的离子性越强。共价键键合强度高于离子键,因此,Mulliken布局数大的化学键,其强度一般较大。表 1中C-O键Mulliken布局数大于Zn-O键,因此前者化学键强度更高。此外,根据表 1所示键长也可得出Zn-O键的强度低于C-O键。
| 表 1 菱锌矿中Mulliken键布局分析 Table 1 Mulliken bond population of smithsonit |
|
2.2 菱锌矿各晶面断裂键密度与表面能 2.2.1 菱锌矿化学键断裂类型对表面能影响
菱锌矿晶体内部存在Zn-O键和C-O键两种类型化学键。根据文献报道[8-13],结合图 2最高衍射峰对应的晶面,确定了(104)、(101)和(001)三个晶面为研究对象,各晶面原子分布规律如图 3所示。
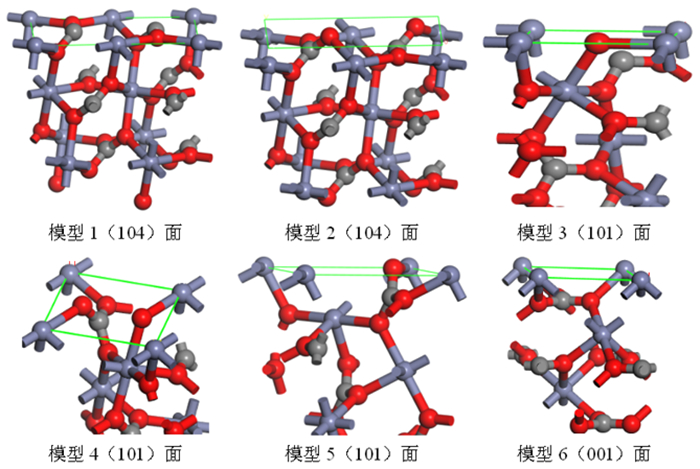 |
| 图 3 菱锌矿不同晶面原子分布(红色—O,黑色—C,蓝色—Zn;绿线所示区域为表面) Fig.3 Atomic distribution on different crystal planes of smithsonite (Red- O, Black- C, Blue- Zn; The green line range are surfaces) |
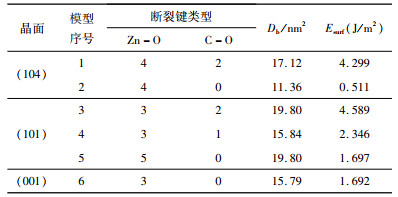
图 3模型1和2为(104)面结构模型,模型1表面O配位数为3,达到饱和。表面每个C与周围2个O结合成2配位,解理时1个C-O键断裂。Zn为4配位,说明解理时每个Zn发生2个Zn-O键断裂。图 2表面C配位数已达到饱和,每个O与周围的1个C和1个Zn配位,由于菱锌矿晶体体相中O与2个Zn和1个C成3配位,因此模型2表面O包含1个O-Zn断裂,同理分析可知表面每个Zn包含1个Zn-O不饱和键。
模型3~5为(101)面三个结构模型,模型3中表面的O与周围的2个Zn配位,根据图 1中O的配位特点可知,该模型表面O所含的不饱和键为O-C键而不是O-Zn键;C和Zn均与O配位,很容易判断出每个Zn包含3个Zn-O不饱和键,每个C包含1个C-O不饱和键。模型4中表面C配位达到饱和,每个Zn发生2个Zn-O断裂;该模型中O虽然都是2配位,但连接的原子存在差异,其中,与2个Zn联结的O在矿物解理时发生断裂的为O-C键,而与1个C和1个Zn配位的O发生断裂的为O-Zn键。同理,模型5中Zn包含4个断裂键,O发生的断裂键为O-Zn键。
模型6为(001)结晶方向解理面模型,图中O、C均已达到饱和,表面Zn配位数为3,因此,解理时仅发生Zn-O键断裂。
根据上述分析和公式(1)、(2),可得各晶面断裂键密度、表面能,计算结果如表 2所示。
| 表 2 菱锌矿不同晶面的断裂键种类、断裂键密度和表面能 Table 2 Broken bond types, density and surface energy of different crystal planes of smithsonite |
|
表 2中断裂键密度大小顺序为(104)模型2 < (001)模型6 < (101)模型4 < (104)模型1 < (101)模型3=(101)模型5, 而表面能大小顺序为(104)模型2 < (001)模型6 < (101)模型5 < (101)模型4 < (104)模型1 < (101)模型3,显然,断裂键密度与表面能无对应关系。仔细分析发现,(104)模型2、(101)模型5和(101)模型6结构模型中全部为Zn-O键断裂,其表面能最小。(101)模型4、(104)模型1和(101)模型3结构模型结构中Zn-O键与C-O键断裂的数量比为3:1、4:2和3:2,由于Zn-O键离子性、键长均大于与C-O(如表 1所示),Zn-O键强度低于C-O键,因此含C-O键的表面结构模型中,C-O键所占的比例越高其表面能也就越高。Zn-O键和C-O键强度不同,断裂后产生的能量必然存在较大差异,因此,两者断裂键密度的加和与表面能也就不存在正比例关系。
晶面的表面能越小,越容易在该结晶方向断裂形成解理面。表 2断裂键密度、类型与表面能的关系表明,菱锌矿解理时晶面只发生Zn-O键断裂,若晶面C-O键断裂将极大增加表面能,不利于该结晶方向解理。由此可见,菱锌矿解理面只有Zn、O位点存在不饱和键,C配位达到饱和,O的配位特性决定了表面O位点必与C配位,或不能同时与2个Zn结合配位(否则发生O-C键断裂)。
2.2.2 菱锌矿晶面表面能与Zn-O断裂键密度的关系根据图 2常出现的几种晶面,借助MS软件,在各结晶方向选取合适的结构模型,使其仅发生Zn-O或O-Zn键断裂,同时C配位数达到饱和。基于密度泛函理论,结合公式(1)和(2)计算各晶面的表面能和断裂键密度,得出Zn-O断裂键密度与表面能的关系,结果如图 4所示。
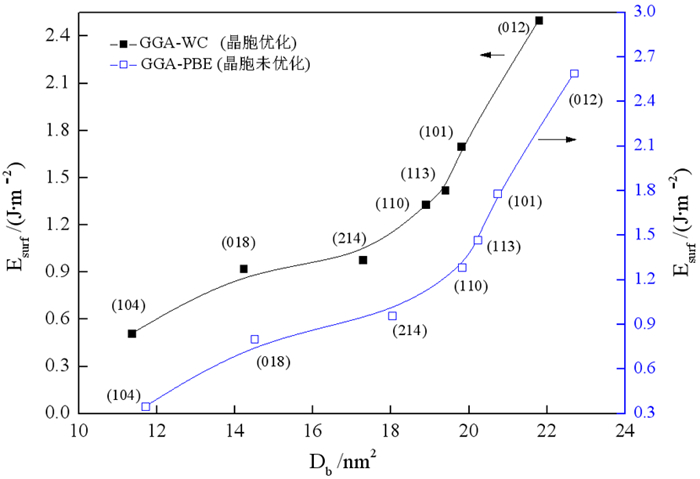 |
| 图 4 菱锌矿晶面断裂键密度与表面能关系 Fig.4 Relationship between broken bond density and surface energy of smithsonite |
由图 4可知,表面能随断裂键密度增加而增加,(104)面断裂键密度和表面能最低,对应于XRD图最高衍射峰(图 2),因此,(104)面是最常见的解理面。从断裂键密度和表面能的角度分析,(018)面和(214)面是仅次于(104)的常见解理面。虽然(012)晶面对应于XRD的次高峰,但该晶面的断裂键密度、表面能最大,且该结晶方向产生的两个表面全部为Zn或O原子,具有强烈的静电引力,不利于产生解理。
2.3 菱锌矿浮选的晶体化学分析与预测矿物表面结构决定浮选行为。基于矿物解理规律分析得出菱锌矿最常见的解理面结构模型,如图 5所示。
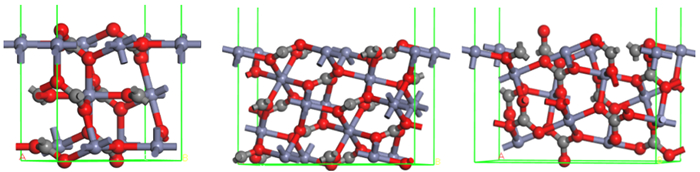 |
| 图 5 菱锌矿常见解理面晶胞模型(红色—C,黑色—C,蓝色—Zn;自左向右分别为(104)、(018)、(214)) Fig.5 Slab model of smithsonite commoncleavage surface(Red- C, Black- C, Blue- Zn; From left to right are (104) (018) (214)) |
图 5中(104)面和(018)面的Zn配位数分别为5和4,表面不饱和的Zn处于同一水平面上。由于(018)面Zn的不饱和度大于(104)面,因此,药剂与(018)面Zn位点的作用强于(104)面。
(214) 面Zn配位数分别为4和5,4配位数的Zn位于最外表面。两种不同配位的Zn在图 5右图中按由左向右的方向上下交错分布。(214)面4配位Zn的最小间距为0.568 nm,而4配位和5配位Zn的最小间距为0.367 nm。羧酸类、羟肟酸类、膦酸类捕收剂、黄药等药剂的两个键合原子间距在0.23~0.31 nm之间,可与矿物表面的1个活性位点成单配位或双配位,以及与2个位点成桥环配位,一般来说,桥环配位方式吸附强度最大。因此,从空间匹配关系角度分析,捕收剂更倾向于与(214)面4配位和5配位的Zn成桥环配位。
基于上述分析,从矿物表面活性位点断裂键特性的角度可预测药剂与(214)面的作用强度低于(018)面,但高于(104)面,即药剂与菱锌矿表面作用存在各向异性。虽然药剂与矿物表面的作用构型需更详细的分子模拟进一步分析确定,但菱锌矿三种表面位点断裂键特性与空间分布规律,为预判药剂作用各向异性、分析分子模拟结果提供了理论参考。
方解石(CaCO3)、白云石[CaMg(CO3)2]是菱锌矿常见脉石矿物,三者同属方解石型晶体结构,已有研究证明(104)面是方解石和白云石最常见解理面[14, 15],结合本文研究可得三种矿物常见解理面和金属位点性质,如图 6和表 3所示。
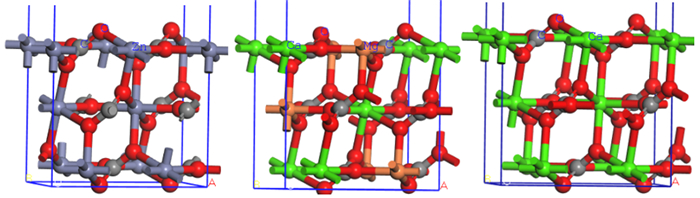 |
| 图 6 菱锌矿(左)、白云石(中)方解石(右)的(104)面位点分布规律示意图 Fig.6 Atomic distribution on (104) plane for smithsonite(left), dolomite(middle) and calcite(right) |
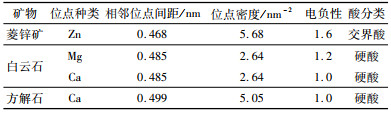
| 表 3 菱锌矿、白云石和方解石(104)面金属位点性质 Table 3 Character of metal sites on the (104) plane of smithsonite, dolomite and calcite |
|
药剂—矿物相互作用能力与矿物表面位点空间分布和活性相关,例如,Zhao研究指出,菱锌矿(101)面存在两种空间位置的Zn位点,位于底部的Zn位点与HS-作用强于顶部的Zn位点[12]。图 6和表 3表明三种矿物常见表面金属位点配位数相同,单位面积内位点数目、相邻位点间距相差较小,且金属位点位于同一水平面,说明位点空间分布特性对三种矿物浮选行为差异的影响较小。通过表 3还可得出,菱锌矿与钙镁碳酸盐矿物的金属位点电负性和酸硬度存在明显差异,是实现浮选分离、筛选高效药剂的重要依据。
根据软硬酸碱理论,Zn2+属于交界酸,Mg2+、Ca2+属于硬酸,药剂的碱硬度越低,越有利于提高菱锌矿与方解石、白云石的分选效果,例如,苯甲羟肟酸的HOMO能级高于油酸钠,前者碱硬度更低,因此油酸钠+苯甲羟肟酸对菱锌矿和白云石分选效果优于单一油酸钠[16];S2-或HS-、黄药属于软碱或交界碱,更容易与交界酸Zn形成共价程度较高的化学键,而难以与硬酸的Mg2+、Ca2+发生化学反应,因此,硫化—黄药浮选法对菱锌矿和钙镁碳酸盐矿物具有高选择性,与浮选实践相符。
3 结论(1) 菱锌矿不同晶面的表面能与Zn-O键断裂键密度成正相关,当C-O键发生断裂时,晶面的断裂键密度与表面能不存在对应关系。菱锌矿解理后只有Zn和O含有不饱和键,且O与C联结,或不能同时与2个Zn结合配位。Zn-O键断裂键密度、表面能均证明(104)面是菱锌矿最常见的解理面,(018)面和(214)面次之。
(2) 菱锌矿各晶面Zn断裂键存在各向异性,根据断裂键性质和空间匹配关系推测药剂与不同晶面Zn的作用强度顺序为:(018)面>(214)面>(104)面。
(3) 菱锌矿与钙镁碳酸盐脉石矿物(方解石、白云石)的解理规律和常见解理面结构模型相似,表面金属位点的化学性质差异(如电负性、酸硬度)是实现矿物分选、筛选高效药剂的重要依据。
| [1] |
李胜荣. 结晶学与矿物学[M]. 北京: 地质出版社, 2010.
|
| [2] |
GOUVEIA A F, FERRER M M, et al. Modeling the atomicscale structure, stability and morphological transformations in the tetragonal phase of LaVO4[J]. Chemical Physics Letters, 2016, 660: 87-92. DOI:10.1016/j.cplett.2016.08.013 |
| [3] |
GAO ZY, SUN W, HU YH. Mineral cleavage nature and surface energy: Anisotropic surface broken bonds consideration[J]. Trans. Nonferrous Met. Soc. China, 2014, 24: 2930-2937. DOI:10.1016/S1003-6326(14)63428-2 |
| [4] |
高志勇. 三种含钙矿物晶体各向异性与浮选行为关系的基础研究[D]. 长沙: 中南大学, 2013.
|
| [5] |
朱一民, 张洋洋, 南楠, 等. 磷灰石晶体及表面基因的第一性原理计算[J]. 金属矿山, 2020(6): 87-93. |
| [6] |
沈智豪, 张谦, 方健, 等. 菱锌矿表面硫化研究进展[J]. 有色金属(选矿部分), 2021(1): 37-46, 59. |
| [7] |
HAN C, LI TT, ZHANG W, et al. Density functional theory study on the surface properties and floatability of hemimorphite and smithsonite[J]. Minerals, 2018, 8(12): 1-13. |
| [8] |
LIU J, ZENG Y, EJTEMAEI M., et al. DFT simulation of S-species interaction with smithsonite (001) surface: Effect of water moleculeadsorption position[J]. Results in Physics, 2019, 15: 102575. DOI:10.1016/j.rinp.2019.102575 |
| [9] |
王瑜, 刘建, 曾勇, 等. 不同硫组分在菱锌矿表面吸附的计算研究[J]. 有色金属工程, 2019, 9(6): 69-75, 83. |
| [10] |
CUI WY, CHEN JH, LI YQ, et al. Interactions of xanthate molecule with different mineral surfaces: A comparative study of Fe, Pband Zn sulfide and oxide minerals with coordination chemistry[J]. Minerals Engineering, 2020, 159: 106565. DOI:10.1016/j.mineng.2020.106565 |
| [11] |
ZHAO WC, LIU DW, FENG QC, et al. DFT insights into the electronic properties and adsorption mechanism of HS on smithsonite (101) surface[J]. Minerals Engineering, 2019, 141: 105846. DOI:10.1016/j.mineng.2019.105846 |
| [12] |
LIU WP, WANG ZX, WANG XM, et al. Smithsonite flotation with lauryl phosphate[J]. Minerals Engineering, 2020, 147: 106155. DOI:10.1016/j.mineng.2019.106155 |
| [13] |
LIU M, CHEN JH, CHEN Y, et al. Interaction between smithsonite and carboxyl collectors with different molecular structure in the presence of water: A theoretical and experimental study[J]. Applied Surface Science, 2020, 510: 145410. DOI:10.1016/j.apsusc.2020.145410 |
| [14] |
高志勇, 孙伟, 刘晓文, 等. 白钨矿和方解石晶面的断裂键差异及其对矿物解理性质和表面性质的影响[J]. 矿物学报, 2010, 30(4): 470-475. |
| [15] |
BAI JZ, WANG JZ, YIN WZ, et al. Influence of sodium phosphate salts with different chain length on the flotation behavior of magnesite and dolomite[J]. Minerals, 2020, 10(11): 1031. DOI:10.3390/min10111031 |
| [16] |
WANG L, HU GY, SUN W, et al. Selective flotation of smithsonite from dolomite by using novel mixed collector system[J]. Transactions of Nonferrous Metals Society of China, 2019, 29(5): 1082-1089. DOI:10.1016/S1003-6326(19)65016-8 |
 2021
2021


