| 可比销售法中参照矿业权优选方法优化 |
可比销售法是市场途径评估方法中较为常用的一种矿业权评估方法,根据《矿业权评估准则》中对其原理的定义[1]:可比销售法是基于替代原则,将评估对象与在近期相似交易环境中成交,满足各项可比条件的矿业权的地、采、选等各项技术、经济参数进行对照比较,分析其差异,对相似参照物的成交价格进行调整估算评估对象价值的方法。
自国土资源部于2006年8月7日以公开摇号方式选择矿业权评估机构后,许多省市县国土资源管理部门也纷纷以公开方式选择矿业权评估机构。这种方式有利于公平竞争和矿业权评估市场体系的完善,使评估机构可以公平、公正地进行矿业权评估。各级国土资源管理部门公示的矿业权评估报告和公开招拍挂出让矿业权的做法,为可比销售法找到相似的具有可比量化的参照物,提供了更多的可能性。故可比销售法逐步推广的时机已日臻成熟[2]。
2017年,根据《中共中央办公厅国务院办公厅关于印发矿业权出让制度改革方案的通知》《国务院关于印发矿产资源权益金制度改革方案的通知》以及《财政部国土资源部关于印发 <矿业权出让收益征收管理暂行办法>的通知》的有关要求,建立矿业权市场基准价制度,征收矿业权出让收益。可比销售法的应用前提是建立参照矿业权数据库,而矿业权市场基准价制度与参照矿业权数据库是密切相关的。一方面各矿种的参照矿业权数据库有利于矿业权市场基准价制度的建立;另一方面各矿种的矿业权市场基准价可以指导参照矿业权的选取,进而影响矿业权出让收益的征收。
可比销售法与矿业权市场的建立、发展以及活跃程度密切相关,从市场的角度对矿业权的出让收益进行客观的评价,最容易被矿业权的交易双方所接受,也最公正、客观。可比销售法可用于评估任何勘查程度的探矿权出让收益,且评估过程较为简单易行。基于以上优点可以预见,在未来的矿业权评估工作中,可比销售法应当成为评估矿业权出让收益的主流方法,其他方法可以作为验证可比销售法、丰富地质资料数据库的辅助方法[3]。
然而在评估矿业权出让收益时,往往需要面对以下两大问题:(1)对地质资料数据库中的数据进行筛选,选取与待评估矿床相似的资料作为参照矿业权。该过程较为困难且工作量巨大,如何在地质资料数据库中快速优选参照矿业权?(2)《矿业权评估准则》中要求选取“近期相似交易环境”中的矿业权信息作为参照矿业权,却未对近期相似交易环境进行定量描述。那么在数据库中如何对“近期相似交易环境”进行筛选?
1 因素分析 1.1 增加市场活跃度因素的讨论《矿业权评估准则》中对于应用可比销售法的条件是“近期相似交易环境成交的,与被评估对象主矿种相同、勘查程度相同或相近、具有可比条件的矿业权交易案例”。在地质资料数据库中,应当将不同矿种、不同勘查程度的矿业权交易案例进行分类存储,根据待评估矿业权的矿种及勘查程度情况代入不同数据库中。
对于“近期相似交易环境”,主要是指参照矿业权要与待评估矿业权的交易时间、交易市场类型、交易背景等因素相似。而以上这些因素不论如何变化,影响两矿业权对比的内在因素永远是矿产品的供求关系以及矿业权市场的活跃程度。例如参照矿业权要与待评估矿业权的交易时间相近,是由于相近的交易时间下各种矿产品的供求关系及矿业权市场的活跃程度变化很小,不会对交易动机产生影响。这也是在发生金融危机前后的矿业权虽然时间相近但无法满足可比销售法条件的原因。
对于参照矿业权的选取,实际上只要满足矿产品的供求关系以及市场活跃度情况相似,就可以与待评估矿业权进行可比销售。因此,倡议在地质资料数据库中添加矿产品及矿业权市场条件指标,通过对比该指标确定是否为“近期相似交易环境”。
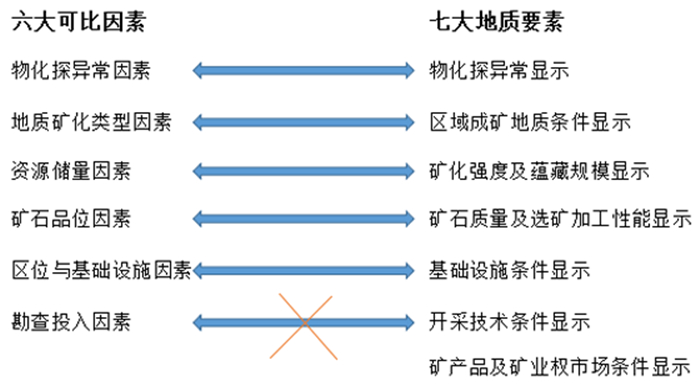
1.2 探矿权评估中替换可比因素的讨论利用可比销售法评估探矿权出让收益的过程中,主要应考虑以下六大可比因素:勘查投入、资源储量、矿石品位、物化探异常、地质矿化类型及基础设施条件。通过对六大可比因素的研究,发现这六大因素与地质要素评序法中专家评判的七大地质要素有较大的联系[4](见图 1)。
 |
| 图 1 各因素对应逻辑图 Fig.1 Logical diagram of correspondence of each factor |
由图 1可知,物化探异常因素与物化探异常显示相对应,地质矿化类型因素与区域成矿地质条件显示相对应,资源储量因素与矿化强度及蕴藏规模显示相对应,矿石品位因素与矿石质量及选矿加工性能显示相对应,且该显示要素比矿石品位更能反映矿石品质及选矿加工成本的高低,区位与基础设施因素与基础设施条件显示相对应。
尽管勘查投入因素与开采技术条件显示无法对应,但我们应当认识到,勘查投入因素实质上无法反映矿床的开采价值,有的矿床勘查投入少但矿床价值大。因为勘探前期地质资料较少,所以利用勘探投入因素[5]。如果将该因素替换为开采技术条件因素,能更好地对比两矿床的价值;此外,地质要素评序法中还有矿产品及矿业权市场条件因素,该因素是由专家根据矿业权评估基准日的矿产品供求关系及矿业权市场的市场流动性等因素确定的,具有较强的权威性与可信性,可以作为“近期相似交易环境”的量化标准。
1.3 在可比销售法中借鉴地质要素参数的优越性与传统评估探矿权的可比销售法相比,收集地质要素评序法的地质参数较为方便、简洁。具体原因如下:
(1) 地质要素评序法是探矿权评估中较为常用的方法,各个种类矿床的地质数据较多,拥有坚实的数据基础。
(2) 地质要素评序法的数据较为直观,可直接用于建立数据库,避免了繁重的矿产资料比对工作。
(3) 众多利用地质要素评序法的探矿权报告虽然不相关,但都按照《矿业权评估准则》中的具体标准进行评估的,具备较强的可比性。
(4) 地质要素评序法中的参数考虑了矿业权市场活跃程度的指标,有利于判断是否为“近期相似交易环境”。
由以上分析可知,地质要素评序法与可比销售法是相通的,完全可以利用地质要素评序法的因素通过可比销售的方法对待评估矿床的探矿权价值进行评估。
2 方法设计 2.1 模糊决策方法概述模糊决策方法[6]是基于模糊数学理论的一种常用的优化方法。它以模糊模式识别、模糊综合评价、模糊聚类分析以及模糊优选等方法为基础,对各种方案按从优到劣的顺序排列,选出最优方案,或判断每一个方案最大可能的所属类别。
2.2 利用模糊决策方法的基本思路收集足够量参照探矿权的地质要素,建立地质要素数据库,再利用模糊聚类分析的方法将地质要素数据根据具体地质情况的相似度进行分组,对每一组参照探矿权地质要素建立模糊数学模型[7],用专家评议法对待评估矿床的地质情况进行估值,通过比对待评估矿床与各个模型的贴近度或隶属度,确定与待评估矿床相近的参照探矿权资料,进而完成对参照探矿权的优选。
2.2.1 建立模糊数学模型收集地质要素资料,以地质要素评序法的各项参数为标准,对已知探矿权信息进行分组整理。由于地质资料数据库数据较多,一一比对地质资料确定参照探矿权是一件费力的事情。故将地质资料按照相似度进行分组,建立模糊数学模型,求每个模型的隶属函数,通过比较待评估矿床与每个模型的贴近度,进行模糊决策缩小决策范围。若数据资料仍然较多时,可迭代此算法,直至缩小范围符合可比销售法标准为止。
利用可比销售法进行探矿权评估,仅仅只有参照探矿权的资料是不够的,还应该有待评估矿床的地质资料,本方法也不例外[8]。通过对待评估矿床各地质勘探资料进行分析,确定待评估矿床的地质情况。可将地质资料交于专家或常年地质工作者,使其根据地质要素评序法的标准给出一个估值范围,建立待评估矿床模糊数学模型,根据该数学模型与其他模型的贴近度,进行模糊决策。
2.2.2 计算综合隶属度当参照探矿权数据资料满足最大贴近度标准时,将参照探矿权的每组数据代入待评估矿床评分模型当中,计算每组数据与待评估矿床地质情况的隶属度,并将每个可比要素的隶属度与其权重相乘[9],计算综合隶属度H:
| $ H=\sum\limits_{i=1}^{n}{{{\mu }_{i}}}\times {{\varphi }_{i}} $ | (1) |
其中μ为各可比要素的隶属度,φ为各可比要素所占权重,n为可比要素个数。
3 实证分析基于以上分析,以山东半岛某金矿(主矿种为银金矿)的探矿权出让收益评估为例,利用模糊决策方法对参照探矿权进行优选。该金矿在2009年通过地质要素评序法进行过探矿权评估,以便验证该方法的可行性。
3.1 数据选取及方法概述收集全国24座同矿种(金矿)、相近勘查程度的矿山的探矿权评估报告,对报告中各矿山利用专家评议法得到的七类地质要素数据进行了整理,建立了地质要素数据库。为便于研究,对24座矿山以字母A~X表示。通过对比待评估矿床与地质要素数据库中的七类地质要素,进而筛选与待评估矿床最相近的参照探矿权信息。
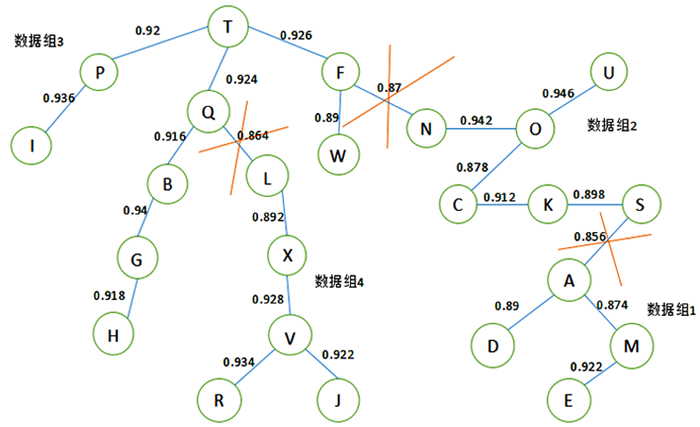
3.2 利用模糊聚类方法对地质资料进行分组建立模糊相似矩阵[10],利用最大树法对各参照探矿权的相似程度进行聚类分组,结果见图 2。
 |
| 图 2 各矿山相似性最大树形图 Fig.2 Tree diagram of Maximum similarity of each mine |
图 2是根据模糊相似矩阵中,各组数据之间的相似性构造的最大树形图。其作图规则[11]为按照模糊相似矩阵中rij从大到小的顺序将各元素依次连接而不产生回路,直到连接完所有元素为止,故最大树形图可以较好地描述各组数据间的相似性。
当阈值λ=0.87时,将地质数据按照地质环境的相似性分为四组。由图 2可知,A、D、E、M为数据组1,其各类可比因素评价较好;C、K、N、O、S、U为数据组2;B、F、G、H、I、P、Q、T、W为数据组3,各类可比因素评价一般;J、L、R、V、X为数据组4,其可比因素评价较差。
3.3 建立模糊数学模型通过对四组数据的研究可知,1、4数据组分别满足偏大、偏小型的正态分布;2、3数据组满足中间型的正态分布[12]。利用各数据组中每一类地质要素的最大、小平均值及方差等数据确定其隶属函数[13],并根据七大可比要素的隶属函数建立四类模糊数学模型。
组1隶属函数模型:
| $ ~{{A}_{1j}}\left( x \right)=\left\{ \begin{align} & \ \ \ \ \ \ \ \ \ \ \ 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\overline{x}}_{j}}\le x\le \text{max} \\ & ~1-\frac{1}{2\sigma _{j}^{2}}{{\left( x-{{\overline{x}}_{_{j}}} \right)}^{2}}\ \ \ {{\overline{x}}_{_{j}}}-\sqrt{2}{{\sigma }_{j}}\le x\le {{\overline{x}}_{_{j}}}~ \\ & \ \ \ \ \ \ \ \ \ \ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0<{{\overline{x}}_{j}}-\sqrt{2}{{\sigma }_{j}}~ \\ \end{align} \right. $ | (2) |
组2隶属函数模型:
| $ {{A}_{2j}}\left( x \right)=\left\{ \begin{align} &1-{{\frac{\left( x-{{a}_{j}} \right)}{2\sigma _{j}^{2}}}^{2}}\ \ \ \ \ {{a}_{j}}-\sqrt{2}{{\sigma }_{j}}<x<{{a}_{j}} \\ &\ \ \ \ \ \ \ \ \ 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{a}_{j}}\le x\le {{b}_{j}} \\ &1-{{\frac{\left( x-{{b}_{j}} \right)}{2\sigma _{j}^{2}}}^{2}}\ \ \ \ \ {{b}_{j}}<x<\ {{b}_{j}}+\sqrt{2}{{\sigma }_{j}} \\ &\ \ \ \ \ \ \ \ \ 0\ \ \ \ \ \ \ \ \ \ \ x<{{a}_{j}}-\sqrt{2}{{\sigma }_{j}}或x>{{b}_{j}}+\sqrt{2}{{\sigma }_{j}} \\ \end{align} \right.\text{ }~ $ | (3) |
组3隶属函数模型:
| $ {{\rm{A}}_{3{\rm{j}}}}\left( {\rm{x}} \right) = \left\{ \begin{array}{l} 1 - {\frac{{\left( {{\rm{x}} - {{\rm{a}}_{\rm{j}}}} \right)}}{{2{\rm{ \mathsf{ σ} }}_{\rm{j}}^{\rm{2}}}}^2}\;\;\;\;\;{{\rm{a}}_{\rm{j}}} - \sqrt 2 {{\rm{ \mathsf{ σ} }}_{\rm{j}}} \le {\rm{x}} < {{\rm{a}}_{\rm{j}}}\\ {\rm{ }}\;\;\;\;\;\;\;\;1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\rm{a}}_{\rm{j}}} \le {\rm{x}} \le {{\rm{b}}_{\rm{j}}}\\ 1 - {\frac{{\left( {{\rm{x}} - {{\rm{b}}_{\rm{j}}}} \right)}}{{2{\rm{ \mathsf{ σ} }}_{\rm{j}}^{\rm{2}}}}^2}\;\;\;\;\;{{\rm{b}}_{\rm{j}}} < {\rm{x}} < \;{{\rm{b}}_{\rm{j}}} + \sqrt 2 {{\rm{ \mathsf{ σ} }}_{\rm{j}}}\\ \;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;0 < {{\rm{a}}_{\rm{j}}} - \sqrt 2 {{\rm{ \mathsf{ σ} }}_{\rm{j}}}或{\rm{x}} > {{\rm{b}}_{\rm{j}}} + \sqrt 2 {{\rm{ \mathsf{ σ} }}_{\rm{j}}} \end{array} \right. $ | (4) |
组4隶属函数模型:
| $ {{A}_{4j}}\left( x \right)=\left\{ \begin{align} &\ \ \ \ \ \ \ \ \ \ \ 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{min}\le x\le {{\overline{x}}_{j}} \\ &1-\frac{{{\left( x-{{\overline{x}}_{j}} \right)}^{2}}}{2\sigma _{j}^{2}}\ \ \ \ \ \ \ \ \ \ \ {{\overline{x}}_{j}}<x\le {{\overline{x}}_{j}}+\sqrt{2}{{\sigma }_{j}} \\ &\ \ \ \ \ \ \ \ \ \ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x>{{\overline{x}}_{j}}+\sqrt{2}{{\sigma }_{j}}~ \\ \end{align} \right. $ | (5) |
表 1到表 4分别为各数据组隶属函数的所需参数。其中,表头各项分别代表七大可比要素;x为各数据组中每种可比要素的平均值;a、b为各数据组中每种可比要素舍弃最大、最小值后所求的最大、最小平均值;σ为各数据组中每种可比要素的标准差;σ2为各数据组中每种可比要素的方差。
| 表 1 组1参数 Table 1 Parameters of group 1 |
 |
| 表 2 组2参数 Table 2 Parameters of group 2 |
 |
| 表 3 组3参数 Table 3 Parameters of group 3 |
 |
| 表 4 组4参数 Table 4 Parameters of group 4 |
 |
3.4 对待评估矿床建立评价模型
根据未知金矿的具体地质信息,以《矿业权评估准则》为标准,对七种可比要素进行专家评议,去除误差较大的数据,确定估值范围,建立待评估矿床模糊模型,具体结果见表 5。
| 表 5 待评估矿床参数 Table 5 Deposits parameters to be evaluated |
 |
待评估矿床隶属函数模型:
| $ {{B}_{j}}=\left\{ \begin{align} &1-\frac{{{\left( x-{{\overline{x}}_{j}} \right)}^{2}}}{2\sigma _{j}^{2}}\ \ \ \ \ \ {{\overline{x}}_{j}}-\sqrt{2}{{\sigma }_{j}} < {{x}}\le {{\overline{x}}_{j}}+\sqrt{2}{{\sigma }_{j}} \\ &\ \ \ \ \ \ \ \ \ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0<{{\overline{x}}_{j}}-\sqrt{2}{{\sigma }_{j}}或x>{{\overline{x}}_{j}}+\sqrt{2}{{\sigma }_{j}} \\ \end{align} \right. $ | (6) |
利用格贴近度法计算待评估矿床与四类数据集的贴近度:
设A、B为U上的两个模糊集,则
| $ N\left( A, B \right)=\left( A\cdot B \right)\mathit{\Lambda }\left( A\odot B \right) $ | (7) |
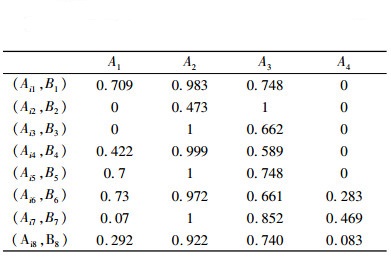
由格贴近度法计算的贴近度如表 6所示。
| 表 6 待评估矿床模型与其他模型贴近度 Table 6 Proximity of the deposit model to be evaluated with other models |
 |
3.6 优选参照探矿权
根据上表所示,数据组2与待评估矿床的贴近度最高,故采用C、K、N、O、S、U六矿的数据与待评估矿床进行对比,将六矿可比数据代入待评估矿床模糊模型,计算六座矿在待评估矿床模型中的隶属度,取隶属度最大的三座矿即为最优参照探矿权。
根据对各矿床综合隶属度的计算可知,O、C、K矿床与待评估矿床最为相似,故O、C、K矿床为最优参照探矿权。
3.7 结果分析综合对参照探矿权优选的结果,可以得到以下结论:
(1) 虽然在地质资料数据库中,O、C、K矿床与待评估矿床最为相似,但仍不满足可比销售法的使用条件。由表中的数据可知,各矿床对于待评估矿床的隶属度都不是很高,甚至还出现隶属度为0的状况,说明选取的参照探矿权与待评估矿床的相似程度较低,不符合《矿业权评估准则》中适用于可比销售法的条件。当各可比因素的隶属度都高于0.85时,说明参照探矿权基本符合可比销售法的条件,可用于进行评价。
(2) 可比因素6是矿产品及矿业权市场条件因素,该因素将矿产品的供求情况及矿业权市场的活跃程度进行了量化,利用该量化参数表示参照探矿权与评估对象交易时间、交易形式、交易信息、交易背景资料相类似的程度。从表 7的隶属度分析中,N矿与待评估矿床最为相似,隶属度为0.993,根据N矿的评估报告,N矿为一级市场中某普查探矿权的出让收益评估,评估基准日为2009年6月,与待评估矿床极为相似。C矿虽然与待评估矿床的地质情况较为相似,但其评估时间、交易背景以及交易形式与待评估矿床有较大差异,故该探矿权信息不符合可比销售法条件。
| 表 7 各矿床在待评估矿床模型中的隶属度 Table 7 The degree of membership of each deposit in the deposit model to be evaluated |
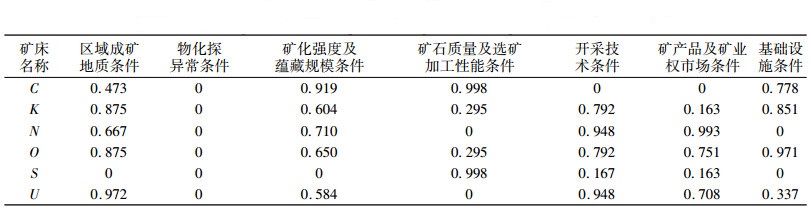 |
(3) 可比因素2在数据组2中隶属度一直为0,但其在数据组3中却具有较高的隶属度。出现这类现象的主要原因是由于收集数据较少,不能将各数据组类别进行细分(建立模糊数学模型需要大量数据为一类),导致数据组2只能满足绝大部分可比因素的相似性,却满足不了全部可比因素。如果收集大量数据,将数据细分为多类,则可满足全部可比因素需要。
4 可行性检验由于以上地质资料数据库中未能找到与待评估矿床相匹配的参照探矿权,故很难说明该方法究竟是否真正可行。为此,笔者将待评估矿床自身的地质要素数据代入待评估矿床模糊数学模型,求其隶属度。由于是同一份地质资料,故地质要素数据应当高度隶属于模糊数学模型,以此来验证当有高度相似的地质资料时,该方法可以将其筛选出来。
由2009年待评估矿床的探矿权评估报告可知,待评估矿床的七大可比要素数据为:1.03、1、2.10、1.03、1.05、1.04、1.02,将数据代入模糊数学模型,求其隶属度,见表 8。
| 表 8 待评估矿床的隶属度 Table 8 The degree of membership of the deposit to be evaluated |
 |
由表 8可知,待评估矿床地质因素在模糊数学模型中具有较高的隶属度,其隶属度普遍在0.99以上,综合隶属度为0.989 5,与模糊数学模型高度匹配,故应用此方法可以筛选地质情况高度相似的参照探矿权。
误差分析:同一份地质资料,建立的模糊数学模型与专家评议得分不能完全匹配,或者说其综合隶属度达不到1,主要原因如下:
(1) 模糊数学模型是根据专家评议的估值范围建立的模型,该模型符合正态分布,隶属度为1的评分范围是根据评分出现的频率所决定的,与评分的数学期望及方差有关,故与传统专家评议法产生误差。
(2) 评分数值的精确度具有差异。为了更精确的表示待评估矿床地质情况的评分覆盖范围,模糊数学模型中的估值范围精确度大致为小数点后三到四位;传统地质要素评序法中,专家对评分精确到点,不需要很大的精确度,大致为小数点后两位,由此产生误差。
5 结语(1) 我国应建立完整的矿业权资料数据库,在评估矿业权出让收益时,可先将待评估矿床资料进行模糊决策,符合条件采用可比销售法,不符合条件再利用其他方法。
(2) 建议添加矿产品及矿业权市场可比因素,用以筛选地质资料数据库中“近期相似交易环境”条件。
(3) 地质要素评序法中各类评价因素具有较多优点,可用于可比销售法。
(4) 对于传统的可比销售法,也可用模糊决策的方法筛选最优参照矿业权。
| [1] |
中国矿业权评估师协会. 中国矿业权评估准则[M]. 北京: 中国大地出版社, 2008.
|
| [2] |
柳海华, 郑宗来, 秦元萍. 可比销售法中参照物选取应注意的问题探讨[J]. 中国矿业, 2010(S1): 64-66. |
| [3] |
张维宸, 鹿爱莉. 国外矿业权转让规制对我国矿业权转让管理的启示[J]. 矿产保护与利用, 2017(4): 1-6. |
| [4] |
苏宏建.矿业权评估中地质要素评序法与可比销售法的对比研究[D].北京: 中国地质大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-11415-1011078624.htm
|
| [5] |
刘勋涛, 靳剑辉. 论矿业权价值评估中存在的几个问题[J]. 中国矿业, 2011(2): 49-52. DOI:10.3969/j.issn.1004-4051.2011.02.013 |
| [6] |
李希灿. 模糊数学方法及应用[M]. 北京: 化学化工出版社, 2016: 50-82.
|
| [7] |
袁怀雨, 苏讯, 刘保顺. 矿业权评估-理论、方法、参数概论[M]. 北京: 中国大地出版社, 2004.
|
| [8] |
许书平, 车如风. 完善部、省矿业权审批权限划分研究[J]. 矿产保护与利用, 2016(3): 8-11. |
| [9] |
陈振华, 余永权, 张瑞. 模糊模式识别的几种基本模型研究[J]. 计算机技术与发展, 2010(9): 32-35. DOI:10.3969/j.issn.1673-629X.2010.09.008 |
| [10] |
高先务. 模糊群决策结果的可信性评估[J]. 数学的实践与认识, 2017(20): 8-14. |
| [11] |
唐淼, 程娴. 最大树聚类法在土壤分析中的应用[J]. 佳木斯大学学报:自然科学版, 2016(6): 968-970. |
| [12] |
李安贵, 张志宏. 模糊数学及其应用[M]. 北京: 冶金工业出版社, 2005: 135-142.
|
| [13] |
王文才, 梁博帅. 基于组合权-模糊数学的多金属矿区资源开发利用效率评价[J]. 矿产保护与利用, 2017(5): 14-23. |
 2019
2019



