| 烧结矿竖罐式冷却过程数值模拟 |
烧结矿余热回收和利用是钢铁余能回收的重要一环。目前我国钢厂主要通过带式冷却机或鼓风式环冷机进行余热回收, 其存在着热回收不完全、冷却空气品质较低、漏风严重等无法完全解决的问题。
基于此, 有学者借鉴了干熄焦冷却回收技术, 提出了烧结矿余热竖罐式回收技术。Chiu和Jang[1]以固定床模型为基础, 将烧结矿料层简化为理想四排球形颗粒, 建立了烧结矿冷却过程的非稳态换热模型, 模拟了烧结矿料层的换热过程。赵斌等[2]通过试验确定了烧结矿中气固传热的平均传热系数, 确定了烧结矿内气固传热形式为层流强制对流换热, 并用Mathematica软件拟合出了气固层流强制对流传热关系式。董辉等[3]建立了竖罐式冷却回收工艺的具体流程, 分析了竖罐式回收工艺的优点与节能作用, 并提出了一些值得研究的问题。田付有等[4]通过试验测量了双粒度混合烧结矿颗粒填充床的压降, 对填充床参数的阻力因子进行分析, 得出了粒度对竖罐式冷却过程压降的影响。
本文在前人的理论研究基础上, 通过仿真模拟软件COMSOL Multiphysics对烧结矿余热竖罐式回收系统进行模拟。结合模拟结果, 对竖罐式回收系统内气体与烧结矿之间的流动和传热过程进行分析, 并引入火用与火用效率的概念, 计算出不同参数下竖罐式冷却过程的冷却效率, 总结出最优的工况参数, 为烧结矿余热高效回收和利用提供一定的参考。
1 竖罐式余热回收工艺流程烧结矿竖罐式余热回收工艺系统主要由冷却装置、除尘装置、余热锅炉、循环风机四部分组成。来自于烧结台车上的高温烧结矿经粉碎之后被引入罐式冷却装置内进行冷却, 待烧结矿完全冷却之后便从罐式冷却装置下部排出进入下一流程。罐体上部排出的高温气体经过一次除尘之后进入冷却锅炉之中进行热回收, 回收完后的低温气体经过二次除尘之后进入循环风机内作为冷却气体再次循环使用。
在整个余热回收系统中, 竖罐式冷却装置是最为核心的部分, 图 1所示为竖罐的简易结构示意图。
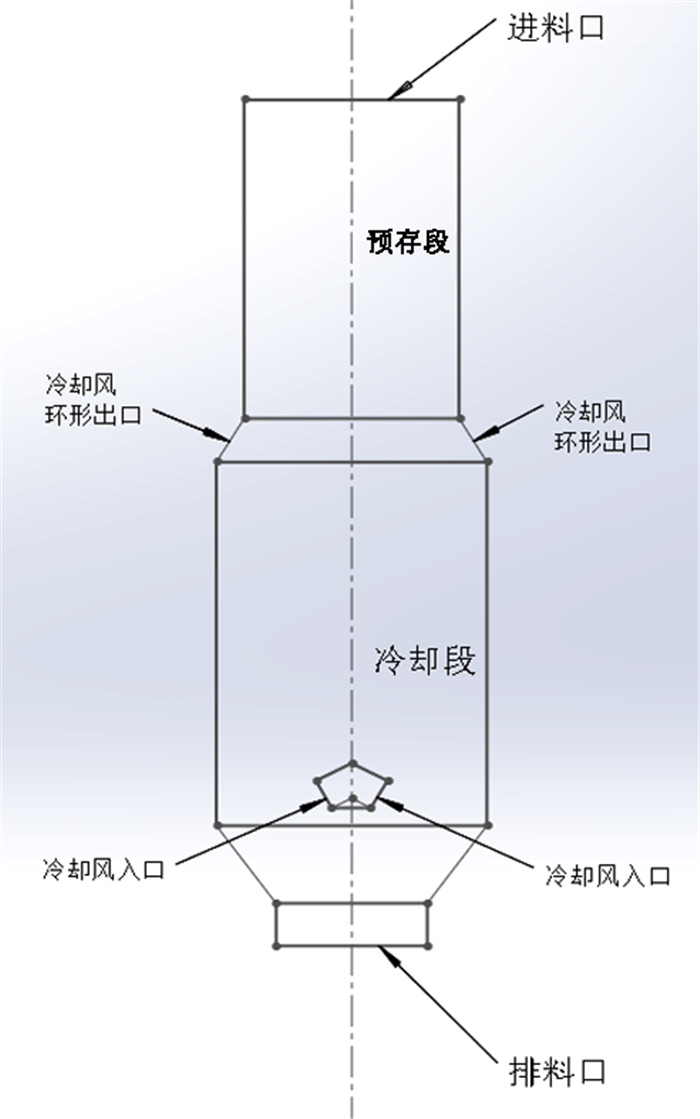 |
| 图 1 竖罐结构示意图 Fig.1 Sketch of the vertical tank |
如图 1所示, 整个竖罐从上至下依次为进料口、预存段、冷却风出口、冷却段、冷却风入口、排料口。高温烧结矿在冷却段与冷却段下部鼓入的冷却空气进行热交换, 冷却完成的烧结矿从底部排料口排出, 随着冷却完成的烧结矿排出, 冷却段内烧结矿料层逐渐向下移动, 上部预存段的高温烧结矿进入冷却段进行冷却。正是这种结构使冷却空气经过的料层高度基本不变, 保证了竖罐内气固接触的稳定性。
2 数学模型烧结矿与冷却气体之间的换热本质上是冷却气体在多孔介质移动床中的强制对流换热过程[5]。冷却气体在多孔介质中的流动和对流换热是非常复杂的问题, 为了方便研究, 本文将其进行一定程度的简化, 并作出以下几点假设:
(1) 竖罐式冷却内的烧结矿是各项同性的多孔介质, 粒度分布均匀, 并且不考虑高温下的形变;
(2) 冷却气体和烧结矿是稳态和达西流运动, 并且忽略壁面效应[6];
(3) 不考虑冷却气体和烧结矿之间的化学反应;
(4) 冷却气体和烧结矿的温度沿径向均匀分布;
(5) 气体为理想气体。
基于以上假设, 根据多孔介质理论和两相局部非热平衡模型[7], 可以得到竖罐内气体换热的数学模型[8]。
(1) 对于冷却气体
| $ \begin{array}{*{20}{l}} {\frac{\partial }{{\partial x}}\left( {{\rho _f}{h_f}{u_f}\varepsilon } \right) + {\rm{ }}\frac{\partial }{{\partial r}}\left( {{\rho _f}{h_f}{v_f}\varepsilon } \right) = }\\ {\frac{\partial }{{\partial r}}\left( {\frac{{\varepsilon {\lambda _f} + {\lambda _d}}}{{{C_{p, f}}}}} \right) + {a_v}\left( {{T_s}-{T_f}} \right)} \end{array} $ | (1) |
(2) 对于烧结矿
| $ \begin{array}{l} \frac{\partial }{{\partial x}}\left[{{\lambda _s}\left( {1-\varepsilon } \right)\frac{{\partial {T_s}}}{{\partial x}}} \right] + \frac{{\partial }}{{\partial r}}\left[{{\lambda _s}\left( {1-\varepsilon } \right)\frac{{\partial {T_s}}}{{\partial x}}} \right] = \\ {a_v}({T_f} -{T_s}) \end{array} $ | (2) |
式中, vf, uf分别表示气体的径向速度和轴向速度, m/s; Ts, Tf分别表示烧结矿和冷却气体的界面平均温度, K; λs, λf分别表示烧结矿和冷却气体的平均导热系数, W/(m·K); λd表示热弥散导热系数, W/(m·K); hf表示流体的焓值, J/kg; ε表示烧结矿孔隙率; Cp, f表示冷却气体比热容, J/(kg·K); av冷却气体与烧结矿颗粒间的体积对流换热系数, W/(m3·K); 可以使用以下经验公式[9]计算av, 表达式为:
| $ \frac{1}{{{a_v}}} = \frac{{{d_p}^{0.75}}}{{M\cdot K\cdot{u_0}^{0.9}{T_f}^{0.3}}} + \frac{{{d_p}^2}}{{75\left( {1-\varepsilon } \right){\lambda _s}}}({\rm{W}}/{{\rm{m}}^3}\cdot{\rm{K}}) $ | (3) |
式中dp为烧结矿当量直径, m; u0为未装入烧结矿时的气体流速, m/s; M为烧结矿粉状系数; K为修正系数。
本文采用数值模拟软件COMSOL Multiphysics对竖罐内气固换热过程进行模拟。考虑到气固换热方程及一些参数需要自行添加, 因此, 本文借助COMSOL Multiphysics软件的自定义方程(PDE)导入气固换热方程及气固两相物性参数随温度变化的方程。
3 模型验证及分析为了确保模拟的结果是可信的, 本文采用宝钢的三期干熄炉为例来进行验证。干熄炉在结构和原理上与竖罐式冷却机十分接近, 仅仅是在内部冷却材料的性质上有区别, 所以, 我们可以通过干熄炉模拟来确定模型是否可信。表 1为宝钢三期干熄炉的主要设计参数[10]。
| 表 1 干熄炉操作参数 Table 1 Operating parameters of CDQ |
 |
表 2是模拟软件计算出的焦炭出口温度和气体出口温度与实测结果的比较。从表 2的结果可以看出, 模拟出的焦炭入口温度与实测值相差24 K, 相对误差为5.1%;气体出口温度的模拟值与实测值相差76 K, 相对误差为6.4%。虽然本模型在模拟过程中忽略了辐射换热、设备漏风率、监测位置不同等因素, 但是模拟结果与实际生产情况基本吻合, 误差基本在可以接受的范围, 因此可以判定该模型的模拟结果是可信的。
| 表 2 模拟结果与实测结果 Table 2 Simulation results and measured results |
 |
4 冷却过程数值模拟与分析 4.1 参数设定
通过前述验证模型验证可知该模拟方法可以用于模拟烧结矿在竖罐内的冷却过程。本文以国内某环冷机实际生产数据为基础进行模拟, 根据模拟结果分析各个因素对冷却效果的影响。环冷机的参数如表 3所示, 模型物性参数设定值如表 4所示。
| 表 3 环冷机参数 Table 3 Ring cooler's parameter |
 |
| 表 4 模型物性参数 Table 4 Model's physical parameters |
 |
| 表 5 空气与烧结矿比热容 Table 5 Specific heat capacity of air and sinter |
 |
4.2 气料比对烧结矿冷却的影响
本节采用宝钢三期干熄焦炉的结构参数进行建模, 同时根据烧结厂实际生产数据, 将气料比设定在1 280 m3/t至2 240 m3/t之间。结果如图 2和图 3所示。
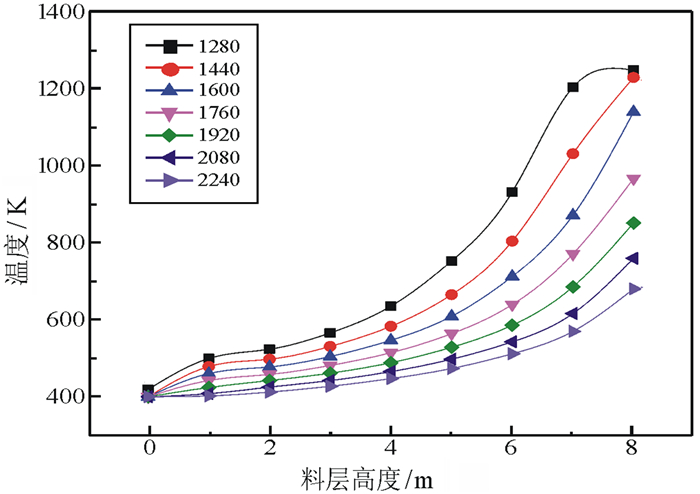 |
| 图 2 不同气料比下烧结矿温度随高度的变化曲线 Fig.2 Sinter temperature varies with the bed height in different air-material ratio |
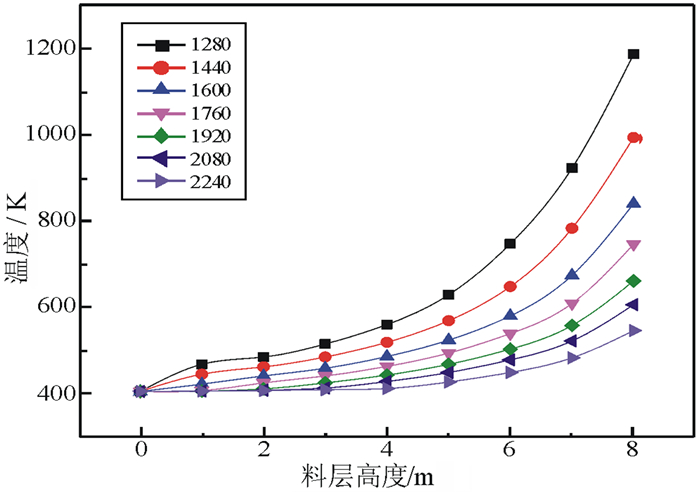 |
| 图 3 不同气料比下气体温度随高度的变化曲线 Fig.3 Gas temperature varies with the bed height in different air-material ratio |
从图 2和图 3的曲线可以看出, 对于烧结矿而言, 随着气料比的增加, 单位时间内通过烧结矿表面的气体量增加, 使得各个料层高度下的烧结矿温度变低; 对于气体而言, 因为气料比的增加, 气体在罐体内部的流速也随之增加, 气体与烧结矿的换热时间减少, 同时烧结矿的温度也随着气料比的增加而降低, 从而使同一高度下的气体温度也随之降低。
图 4和图 5是不同气料比下竖罐冷却段中烧结矿的温度分布图。图中选取了竖罐冷却段的截面并用颜色来反映竖罐中烧结矿的温度, 颜色越接近白色表示温度越高, 颜色越接近红色则表示温度越低。通过图 4和图 5可以看出, 由于竖罐式冷却装置的冷却风出口处于竖罐侧边, 使得冷却气体在向上运动时也在向两侧运动, 竖罐上部靠近中心的部分气体流动性较差, 导致中心部分的烧结矿温度高于两侧的温度。随着气料比的增加, 进入罐内的冷却气体增加, 竖罐中烧结矿的低温区域也随之增加。这种温度分布使得冷却气体与烧结矿的换热主要集中在罐体上部靠近冷却风出口的位置, 罐体下部的换热过程进行的十分缓慢。同时由于罐体内特殊的气体流动方式和烧结矿的多孔特性, 使靠近中心部分的烧结矿冷却速度十分缓慢, 随着气料比的增加, 中心部分烧结矿的冷却速度也没有显著的加快。
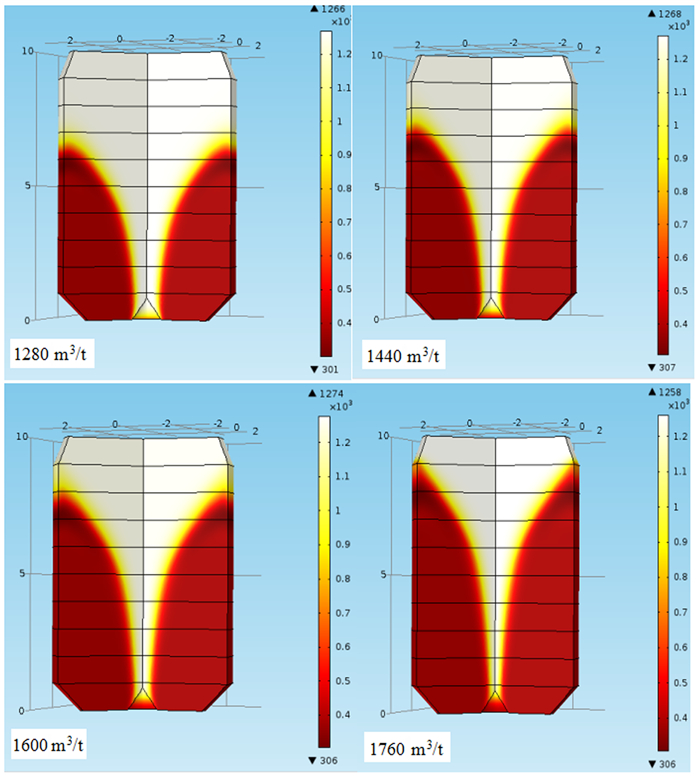 |
| 图 4 1 280 m3/t~1 760 m3/t气料比下烧结矿温度分布 Fig.4 Sinter's temperature distribution between 1 280 m3/t to 1 760 m3/t ratio of gas to material |
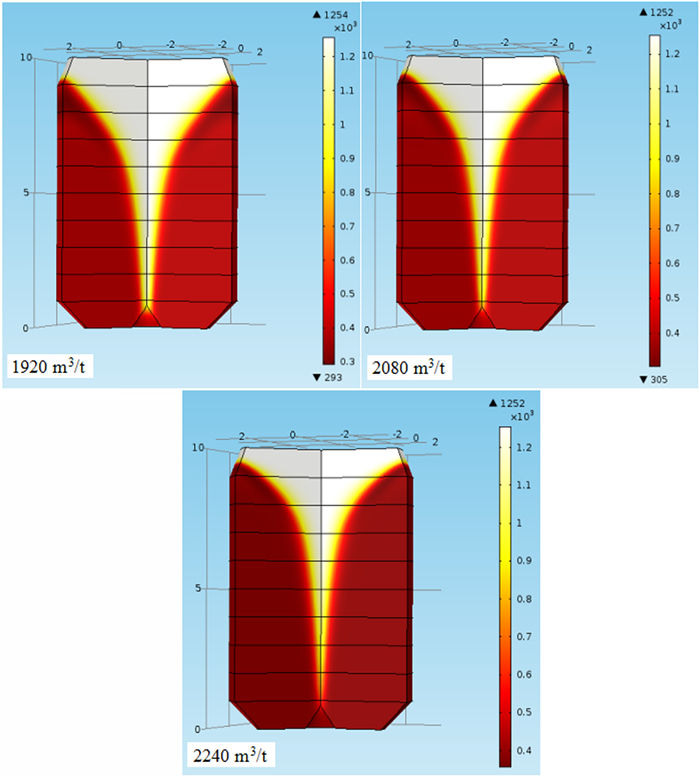 |
| 图 5 1 920 m3/t~2 240 m3/t气料比下烧结矿温度分布 Fig.5 Sinter's temperature distribution between 1 280 m3/t to 1 760 m3/t ratio of gas to material |
图 6是不同气料比下气体的火㶲值[12], 从表中可以看出, 在气料比处于1 280 m3/t~1 600 m3/t之间时, 气体的㶲值较高, 在气料比为1 440 m3/t时, 㶲值为最大值。根据图 6的结果可以看出, 在当前工况下, 最佳的气料比应处于1 280 m3/t ~ 1 600 m3/t之间。
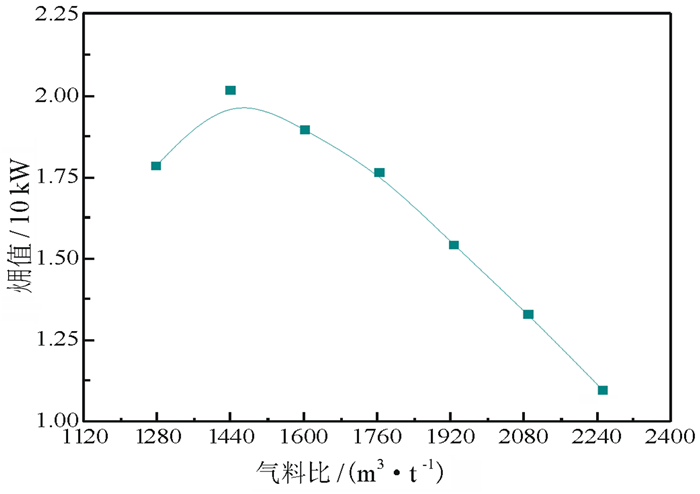 |
| 图 6 不同气料比下气体㶲值 Fig.6 The value of the gas exergy in different ratio of gas to sinter |
4.3 孔隙率对烧结矿冷却的影响
本节同样采用与宝钢三期干熄焦炉相同的结构模型进行建模, 并将内部烧结矿的孔隙率分别设置为0.45、0.47、0.49、0.51、0.53、0.55六个值, 在罐内温度达到稳定之后, 分别测出各个料层高度的平均温度。结果如图 7和图 8所示。
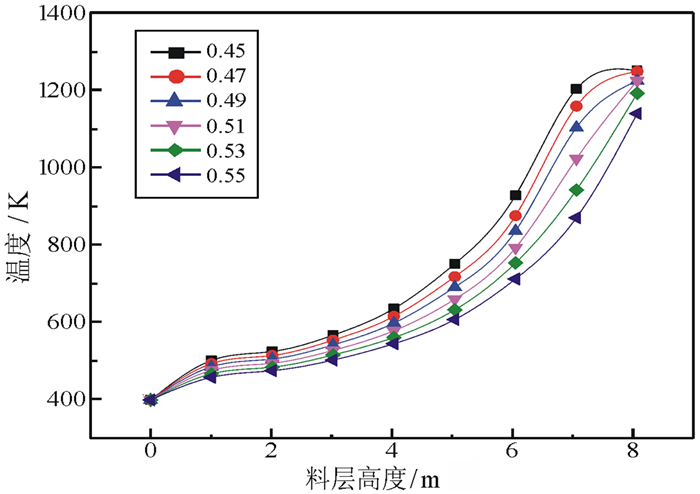 |
| 图 7 不同孔隙率下烧结矿温度随高度的变化曲线 Fig.7 Sinter temperature varies with the bed height in different porosity |
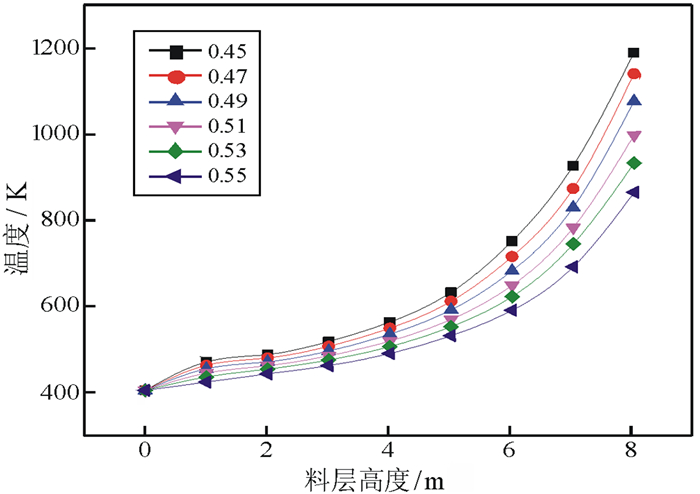 |
| 图 8 不同孔隙率下气体温度随高度的变化曲线 Fig.8 Gas temperature varies with the bed height in different porosity |
虽然罐内各个高度的烧结矿温度是随着孔隙率的增加而降低, 但是烧结矿的密度也随着孔隙率的增加而降低, 烧结矿温度的变化并不能直接反映冷却效率的变化, 所以我们利用火用效率[13]来表示冷却效率。
在不同孔隙率情况下, 烧结矿的排矿温度差距不大, 并且排矿温度较低, 所以我们忽略其对火用效率的影响。烧结矿的输入㶲值可以由式(4)得出:
| $ {E_1} = \int_{{T_{{s_0}}}}^{{T_s}} {{m_1}} {C_{{p_1}}}{\rm{d}}{T_1}-{T_{{s_0}}}\int_{{T_{{s_0}}}}^{{T_s}} {{m_1}\frac{{{C_{{p_1}}}}}{{{T_1}}}{\rm{d}}{T_1}} $ | (4) |
式中:E1为烧结矿的输入值, Ts为烧结矿的初始温度, Ts0为烧结矿排出竖罐时的温度, T1为烧结矿的温度, Cp1为烧结矿的比热容, m1为单位时间排出的烧结矿质量。由于竖罐式冷却装置单位时间内排出烧结矿的体积是不变的, 而孔隙率的变化会改变烧结矿的堆密度, 所以排出烧结矿的体积与孔隙率的关系如式(5)所示:
| $ {m_1} = {\rho _1}V(1-\varepsilon ) $ | (5) |
式中:ρ1为烧结矿的真密度, V为单位时间内排出烧结矿的体积, ε为烧结矿的孔隙率。从式(4)、(5)可以得出烧结矿的输入值为:
| $ {E_1} = {\rho _1}V(\int_{{T_s}_0}^{{T_s}} {{C_{p1}}} {\rm{d}}T-{\smallint ^{{T_s}}}{T_s}_0\frac{{{C_{{p_1}}}}}{{{T_1}}}{\rm{d}}T)\left( {1-\varepsilon } \right) $ | (6) |
式(6)中, ρ1、V、Cp1均为烧结矿的物性参数, ρ1和V数值不变, Cp1会随着温度的变化而变化。Ts0、Ts分别为烧结矿排出竖罐时的温度和烧结矿的初始温度, 烧结矿的初始温度已知为1 250 K, 根据图 7可知烧结矿排出竖罐时的温度为404 K。由于Ts和Ts0在各个孔隙率下均为相同的值, 式(6)中两个定积分的值在不同的孔隙率下也均为相同的值, 那么烧结矿的输入值只会随着孔隙率的变化而变化, 我们可以将式(6)简化为:
| $ {E_1} = G(1-\varepsilon ) $ | (7) |
式中G为一个定值常数。
空气的输出值可以由下式表示:
| $ {E_2} = {\smallint_{{T_{g0}}} ^{{T_s}}}{m_2}{C_{p2}}{\rm{d}}{T_2}-{T_{g0}}{\smallint ^{{T_g}}}{T_{g0}}{m_2}\frac{{{C_{{p_2}}}}}{{{T_2}}}{\rm{d}}{t_2} $ | (8) |
式中:Tg为出口空气温度, Tg0为进口空气温度, m2为单位时间内排出空气的质量, Cp2为空气的比热容, T2为空气的温度。由表 5可知空气的比热容是随温度的变化而变化的, 利用Origin软件对表 5的数据进行拟合, 可以得到空气比热容随温度的变化。
| $ {C_{p2}} = 0.136{\rm{ }}3{T_2} + 969.614{\rm{ }}3 $ | (9) |
由式(8)、(9)可以得到空气的输出㶲值为:
| $ \begin{array}{l} {E_2} = {m_2}[0.068{\rm{ }}15\left( {{T_g}^2-{T_{g0}}^2} \right) + \\ 969.478\left( {{T_g}-{T_{g0}}} \right)-969.614{\rm{ }}3{\rm{ln}}\frac{{{T_g}}}{{{T_{g0}}}}] \end{array} $ | (10) |
效率可以由下式表示:
| $ \eta = \frac{{{E_2}}}{{{E_1}}} = \frac{{{m_2}}}{G} \cdot \frac{{0.068{\rm{ }}15({T_g}^2-{T_{g0}}^2) + 969.478({T_g}-{T_{g0}})-969.614{\rm{ }}3{\rm{ln}}\frac{{{T_g}}}{{{T_{g0}}}}}}{{1 - \varepsilon }} $ | (11) |
通过式(11)计算可得, 孔隙率为0.45、0.47、0.49、0.51、0.53、0.55时, 效率分别为
在烧结矿冷却过程中, 对流换热效率是影响冷却效果最主要的因素。竖罐装置的气料比与烧结矿自身的孔隙率是影响竖罐内对流换热效率的两大因素。随着竖罐装置的气料比增加, 进入烧结矿的冷却气体量增加, 流经烧结矿的冷却气体速度也会随着冷却气体量的增加而增加, 竖罐内的对流换热系数也会增加, 所以烧结矿各个高度的温度会随着气料比的增加而降低。
在烧结矿气料比不变的情况下, 随着烧结矿孔隙率增加, 烧结矿内部孔隙增多, 烧结矿的料层阻力随之减小, 使得烧结矿内冷却气体流速增加, 对流换热系数增大, 所以各个高度的温度随着孔隙率的增加而降低。
5 结论(1) 采用宝钢三期干熄焦炉的数据对模型进行了验证, 确定了该模型的可行性, 可以作为烧结矿余热竖罐式回收过程的模型。
(2) 影响余热竖罐式回收过程的主要因素有气料比和烧结矿孔隙率。在保持其他工况不变的情况下, 随着气料比的增加, 烧结矿和冷却气体的温度随之降低, 气体的㶲值则出现先增加后减少的趋势; 随着烧结矿孔隙率的增加, 烧结矿和冷却气体的温度随之降低, 烧结矿的火用效率也随着孔隙率的增加而降低。
(3) 在保证生产需求的范围内, 竖罐内气料比应控制在1 280~1 600 m3/t之间, 烧结矿的孔隙率应调整至0.45左右。
| [1] |
Jang J Y, Chiu Y W. 3-D transient conjugated heat transfer and fluid flow analysis for the cooling process of sintered bed[J]. Applied Thermal Engineering, 2009, 29(14-15): 2895-2903. DOI:10.1016/j.applthermaleng.2009.02.012 |
| [2] |
赵斌, 赵利杰, 屈婷婷, 等. 环冷机内烧结矿通道气固传热实验关联式[J]. 热科学与技术, 2013, 12(4): 302-306. |
| [3] |
高建业, 刘一伟, 冯军胜, 等. 烧结矿余热回收中试竖罐结构和操作参数解析[J]. 钢铁研究学报, 2017, 29(1): 13-18. |
| [4] |
田付有, 黄连锋, 范利武, 等. 双粒度混合烧结矿颗粒填充床压降实验[J]. 浙江大学学报(工学版), 2016, 50(11): 2077-2086. DOI:10.3785/j.issn.1008-973X.2016.11.006 |
| [5] |
Jik-changLeong, Kai-wunJin, Jia-shyanShiau, 等. Effect of sinter layer porosity distribution on flow and temperature fields in a sinter cooler[J]. 矿物冶金与材料学报, 2009, 16(3): 265-272. |
| [6] |
李俊明, 王补宣, 彭晓峰. 气体在微圆管内层流换热的壁面效应的研究[J]. 工程热物理学报, 1998, 19(5): 596-600. |
| [7] |
郑坤灿, 温治, 王占胜, 等. 前沿领域综述—多孔介质强制对流换热研究进展[J]. 物理学报, 2012, 61(1): 14401-014401. |
| [8] |
力杰. 烧结余热竖罐式回收过程传热数值计算[D]. 沈阳: 东北大学, 2011.
|
| [9] |
许明超, 冯妍卉, 张欣欣, 等. 考虑燃烧反应的干熄炉内一维传热模拟[J]. 冶金能源, 2006, 25(4): 16-19. DOI:10.3969/j.issn.1001-1617.2006.04.006 |
| [10] |
冯军胜, 董辉, 高建业, 等. 烧结矿余热回收竖罐内气固传热过程数值分析[J]. 中南大学学报(自然科学版), 2017, 48(11): 3101-3108. |
| [11] |
罗远秋. 烧结矿冷却过程实验与数值模拟研究[D]. 沈阳: 东北大学, 2009.
|
| [12] |
高建业, 冯军胜, 董辉. 烧结矿余热竖罐式回收利用工艺热力学分析[J]. 冶金能源, 2017, 36(2): 8-13. DOI:10.3969/j.issn.1001-1617.2017.02.002 |
| [13] |
陈刚. 环冷机余热回收系统火用分析与数值模拟[D]. 北京: 中国舰船研究院, 2014.
|
 2018
2018 
