| 钽铌粗精矿高梯度磁选数值法分析 |
钽(Ta)、铌(Nb)都属于高熔点、高沸点稀有金属,在电子工业、化学工业、特种合金以及真空技术等应用领域都具有非常重要的地位。钽铌矿选矿一般采用重选先丢弃大部分脉石矿物,获得低品位混合粗精矿,然后采用多种选矿方法如重选、浮选、电磁选或选冶联合工艺进行精选,从而达到多种有用矿物的分离[1-2]。近年来,许多学者在钽铌浮选药剂的选择、研制方面做了大量工作,发现了许多选择性好的捕收剂。但由于药剂价格及环境影响问题,目前只有国外少数铌矿山采用浮选方法。
具有工业价值的钽铌矿物主要有钽铁矿、铌铁矿、细晶石等,其中以对铌钽铁矿的研究居多。由于铌铁矿等为弱磁性矿物,孙仲元[3]、张成强等[4]先后对栗木锡矿尾矿、非洲某钽铌粗精矿进行高梯度磁选钽铌的试验研究,试验结果表明:通过采用不同磁场强度进行分阶段选别能有效实现铌铁矿的分离,可以得到较高品位和回收率的铌铁矿精矿。随着越来越多的难选钽铌资源的开发,磁选方法将在钽铌矿粗精矿的分选中发挥重要的作用。
目前高梯度磁选的理论研究多围绕单丝介质捕集理论展开,或采用实物模拟方法对其捕集效果进行研究,这些研究对高梯度磁选实践的指导能力还需提高。本文以某富铪锆矿粗精矿为研究对象,结合高梯度磁选试验研究,用数值解析法分析高梯度设备内的磁场特性以及磁性颗粒在磁场中的受力情况,估算出不同条件下矿粒的产率和回收率等,计算结果与高梯度磁选试验结果一致。
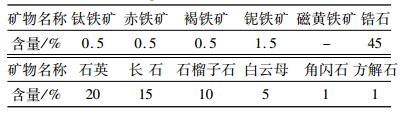
1 某钽铌粗精矿高梯度磁选试验 1.1 原矿性质及特征本试验矿石的原矿为来自某富铪锆矿经重选粗选后获得的粗精矿,锆品位为45.62%,铌含量为3.13%。原矿粒度为-0.2 mm含量占95%,泥化现象较少,矿物的单体解离度都很高,在精选前无需再进行磨矿。矿石中铌钽呈铌铁矿、细晶石两种矿物出现,主要以铌铁矿赋存,少量钽分布于铌铁矿中,铌铁矿占总铌量的80%。脉石主要为石英和长石。矿物中磁性部分还有石榴石、细晶石、褐铁矿和锈蚀铁屑等。矿物组成及其相对含量、XRF多元素分析结果、主要磁性矿物的物性参数见表 1~表 3。
| 表 1 矿石的矿物组成及其相对含量 Table 1 Mineral composition and relative amount of raw ore |
 |
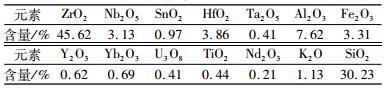
| 表 2 粗精矿多元素分析 Table 2 Multi-element analysis results of run-of-mine ore |
 |
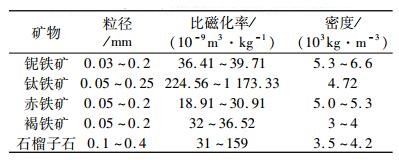
| 表 3 磁性矿物的物性参数 Table 3 Physical parameters of magnetic minerals |
 |
1.2 试验设备及方法
试验采用Slon-100实验型周期式脉动高梯度磁选机,每次试验前将200 g待分选物料加水配制成固体浓度为25%的矿浆,并置于揽拌槽内搅拌10 min作为样品(即高梯度磁选给矿)。磁介质为直径2 mm空隙3 mm交叉排列的不锈钢棒条(SUS 430),当介质盒置于分选器内后注水并开启脉动机构,调节液面至淹没介质盒并保持液面稳定。通电后调整激磁电流使背景磁感应强度达到预定值后,边搅动待分选矿浆边匀速将其倒入分选器内,磁选水流量为0.372 m3/h,脉冲180次/min。给矿结束后停止向分选器补水,切断激磁电流,清洗介质盒。
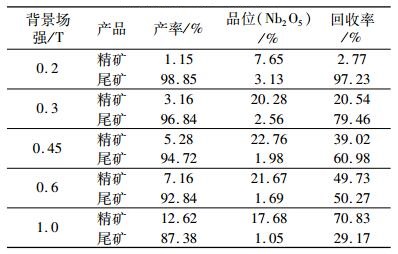
1.3 试验结果所有分选试验均为1次选别,所得精矿和尾矿分别称重、化验铌品位、计算产率和铌回收率。最终试验结果见表 4。
| 表 4 粗精矿高梯度磁选试验结果 Table 4 Results of high gradient magnetic separation on the run-of-mine ore |
 |
2 高梯度磁场特性解析 2.1 磁场力分布
磁场力分布是影响磁选效率的主要因素,但是一直难以求解。保角变换能处理边界形状比较复杂的问题,是求解Laplace的一种有效方法。在高梯度磁场分析过程中,它可以将用复杂多边形表示的简化二维磁场模型变换到一个能用解析法描述的简单区域(矩形或圆形)进行求解,从而简化边界条件。Laplace方程不变性原理使得保角变换前后磁势保持不变,通过对简单区域求解结果的逆运算可获得原多边形简化模型内的气隙磁场分布情况。
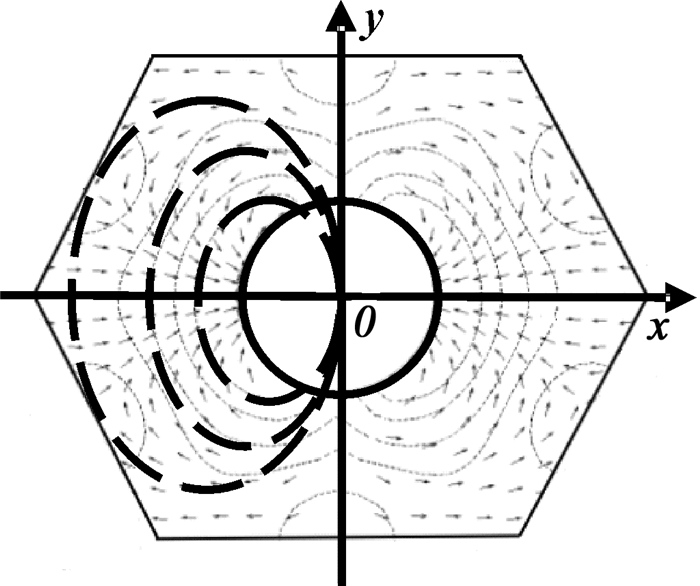
图 1为在Matlab中通过一系列保角变换(包括分式线性变化、椭圆函数变换、许瓦兹-克里斯托夫变换等)求解获得的高梯度磁场内单根棒介质周围磁场力分布的示意图,高梯度磁场内单根棒介质周围磁场分布具有一致性。图中小箭头为磁场力方向,长箭头为磁场方向。实际的磁场力计算过程比较复杂,具体参考相关文献资料[5-8]。
 |
| 图 1 HGMS内磁场力分布示意图 Fig.1 Sketch mao of magnetic traction force in HGMS |
2.2 磁场力近似计算方法
由图 1知,多丝介质磁场与单丝介质磁场具有一定的相似性,但磁场力数值差异较大,单丝介质公式不适用于多丝介质磁场。其最大值为:
| $ \begin{array}{l} {F_{{\rm{max}}}} = |H\frac{{\partial H}}{{\partial r}}{|_{{\rm{max}}}} = \\ \frac{{H_0^2}}{{{R^3}}}\cdot\left( {1 - \frac{1}{{{R^2}}}} \right) - \frac{{H_0^2}}{{{m^3}}}\cdot\left( {1 - \frac{1}{{{m^2}}}} \right) \end{array} $ | (1) |
最小值为:
| $ \begin{array}{l} {F_{{\rm{min}}}} = |H\frac{{\partial H}}{{\partial r}}{|_{{\rm{min}}}} = \\ \frac{{H_0^2}}{{8{{\left( {R + L} \right)}^3}}}\cdot\left( {1 - \frac{1}{{4{{\left( {R + L} \right)}^2}}}} \right) \end{array} $ | (2) |
在以相邻棒介质中心点连线构成的直角坐标系中,最大值与最小值分别位于棒介质与磁场方向坐标轴的交点以及坐标轴原点上。将单介质周围分选空间划分为由相邻棒介质中心线组成的六边形单元区域来进行分析。由磁场力等值线特点及磁场力箭头指向,有效捕集区域内的磁场力等值线用两组通过棒介质圆心点的偏心椭圆簇来近似表示。相邻棒介质中心线均为其中一椭圆(椭圆C)的切线(中心点为切点),该椭圆内部区域可视为磁性颗粒最大捕集区域。
图 2为单元区域内单侧磁场力拟合示意图,由偏心椭圆簇的切点及相交点坐标,在文中给定条件下,椭圆簇的偏心率为:e=0.734 89。
 |
| 图 2 磁场力等值线拟合椭圆 Fig.2 Ellipses fit about the magnetic traction force |
当拟合椭圆长轴2a≤R时,其磁场力表达式为:
| $ \begin{array}{l} F\left( x \right) = |H\frac{{\partial H}}{{\partial r}}| = \\ \frac{{H_0^2}}{{{x^3}}}\cdot\left( {1 - \frac{1}{{{x^2}}}} \right) - \frac{{H_0^2}}{{{m^3}}}\cdot\left( {1 - \frac{1}{{{m^2}}}} \right) \end{array} $ | (3) |
式中:R为棒介质半径,L为平行于磁场方向上的介质间距,m与x分别为六边形及拟合椭圆簇与x轴的交点的绝对值。
联合公式(1)~(3)以及近似椭圆,能获得有效捕集区域内磁场力的近似分布。
3 钽铌粗精矿高梯度磁选数值法分析 3.1 磁性颗粒受力分析在二维空间中对磁性颗粒在复合力场中受力的情况进行分析,在颗粒流体系统的许多研究中,颗粒群的运动采用简化的颗粒动力学进行处理。磁性颗粒将其假设为完全单体解离的强磁性颗粒并视作是形状均一、半径一致的球体。
本试验矿石为除石榴石外,颗粒粒径较小且粒度分布范围窄,可视为均匀的理想颗粒(取平均粒径为0.1 mm),石榴石粒径设为0.2 mm。忽略颗粒存在对流体的影响,考察已知流场中单颗粒的运动,单体颗粒在流体中运动会受到磁力、重力、流体阻力及其它不同力的影响。
其中,磁力计算公式为[9]:
| $ {F_m} = m\cdot{f_m} = \frac{4}{3}\pi \rho d_p^3{\mu _0}{x_0}{H_0}grad{H_0} $ | (4) |
在高梯度磁选中, 设矿粒为匀速运动,根据流体绕流理论[10]来计算聚磁介质周围矿浆的流度。本文试验条件下, 颗粒平均粒径为0.1 mm, 雷诺数Rep∈(1.3, 20), 颗粒所受流体拖曳力大小采用过度区阿连阻力公式计算[11]:
| $ {F_d} = 1.25\pi \sqrt {\eta d_p^3{v^3}{\rho _f}} $ | (5) |
式中:m、ρ、dp、x0分别为矿粒质量、密度、直径、比磁化系数;μ0为载体的磁导率;H0为背景场强;η为矿浆黏度,ρf为载体密度;fm为磁场力;v为颗粒相对流体的运动速度。
颗粒相对流体的运动主要受磁场作用力的影响,计算区域内其初速度为0,由于磁场力的计算采用网格方法,相同磁感应线上任意点的磁速度可以用网格上的数值来计算。设Δfm和Δs为节点上的磁场力及位移变化,则磁速度变化Δv为:
| $ \Delta v = \sqrt {2\Delta {f_m}\cdot\Delta s} $ | (6) |
颗粒在实际运动过程中还受到重力和布朗力等其他力的作用,其与磁场力和流体曳力存在量级差。
3.2 单元磁场颗粒捕集区域分析在高梯度磁选过程中, 磁性矿粒与非磁性矿粒分离的主要条件是磁力大于竞争力。磁性颗粒的捕获主要取决于磁场力及流体阻力差值及二者合力的方向。当二者的差值小于颗粒重力或合力方向偏离棒介质,则颗粒不能被捕集。由于分选磁场为静态,而矿浆为流态,使计算过程变得十分复杂。下文将采用“瞬时快照法”来对磁选过程进行分析,即设定矿浆运动为静态。设分选区矿浆流速为Vd,磁速度为Vf,则式(5)中:
| $ v = {V_d} - {V_f} $ | (7) |
由于不可压缩流体的流函数和势函数同样满足Laplace方程,矿浆流线和磁场强度等势线也呈一致,颗粒所受流体拖曳力主要由磁速度变化引起。通过计算和比较X轴上颗粒在不同条件下受到的磁场作用力及流体拖曳力(此时Vd的方向平行于Y轴,而Vf与X轴平行),能够确定捕集椭圆在X轴上的坐标(即捕集临界值)。
当背景场强为1 T时,单元磁场中X轴上单颗粒铌铁矿受力计算比较结果见图 3。此时,棒介质材料已达到磁饱合,需对磁场力进行修正。
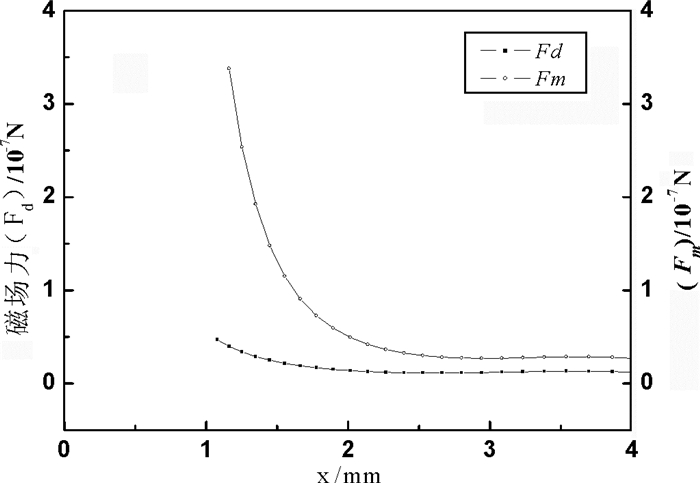 |
| 图 3 X轴上单颗粒铌铁矿受力比较(B=1 T) Fig.3 Comparison of force acted on single particles of Niobite along X-axis |
在图 3中,当x≤2 mm时,颗粒所受磁场力明显大于流体拖曳力,其量级为10-7 N,而颗粒所受重力最大为3.14×10-9 N,因此椭圆(a=1 mm)内的铌铁矿能完全捕集。最终铌铁矿捕集区域的临界值为x=2.66 mm,即其捕集范围为短轴b=x/2的椭圆组合与圆棒交叉的区域。其它磁性矿粒的捕集区域均采用同样的计算方法来确定。不同背景情况下颗粒的捕集区域在X轴上的临界值如图 4所示。
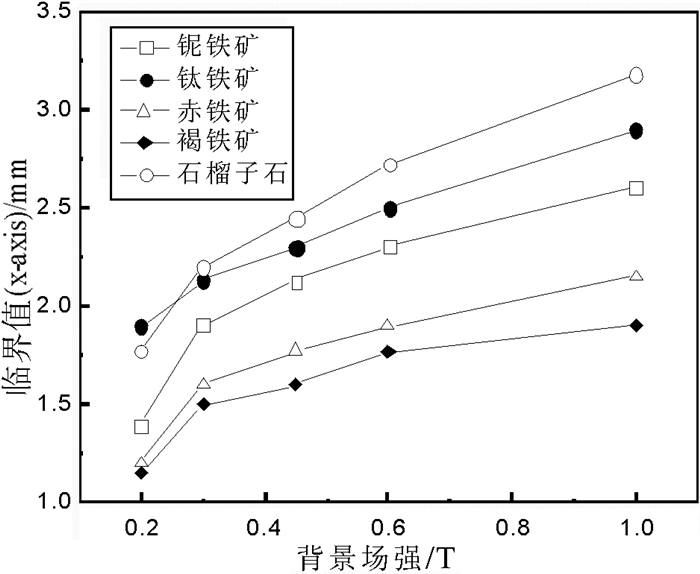 |
| 图 4 捕集区域的临界值(X轴) Fig.4 Critical values of the capture area(X-axis) |
图 4中,不同磁性颗粒的捕集范围均随着背景场强的提高而逐渐扩大,捕集区域大小依次为:褐铁矿 < 赤铁矿 < 铌铁矿 < 钛铁矿 < 石榴石。
当背景场强为1 T时,石榴石和钛铁矿的临界值已经超出六边形区域(x>2.778),这意味着区域内的非磁性颗粒夹杂机率将大大增加,而铌铁矿的临界值也接近区域边缘,因此继续提高背景场强对铌铁矿回收率的影响有限,反而会降低精矿品位。
3.3 颗粒捕集效率计算方法由原粗精矿中Nb2O5品位、矿物组成及不同矿物捕集区域的计算结果等参数,能计算确定铌铁矿的产率、回收率和品位。以B0=0.6 T时的数值计算结果为例,相关计算过程如下。
精矿中Nb2O5回收率计算公式为:
| $ \varepsilon = k = \frac{{2\pi \times 1.15 \times 1.688 - \pi }}{{25 - \pi }} = 41.43\% $ | (8) |
精矿产率计算公式为:
| $ W = \sum\limits_1^n {{\alpha _i}{k_i}} = 7.34\% $ | (9) |
精矿中Nb2O5品位的计算公式为:
| $ \beta = \frac{{\alpha \times \varepsilon }}{{\sum\limits_1^n {{\alpha _i}{k_i}} }} = 17.77\% $ | (10) |
式中:α为原矿中Nb2O5品位,k为铌铁矿有效捕集区域与六边形区域面积的比值,ai为不同捕获磁性矿物在原矿中的比例,ki为不同捕获磁性矿物有效捕集区域与六边形区域面积的比值(面积计算均不包含圆棒区域)。
4 结果与讨论经计算,背景场强在0.2~1 T范围内铌铁矿精矿的回收率、品位(Nb2O5)及产率的实测值(P)与计算值(C)的比较如图 5~图 6所示。精矿的回收率、品位(Nb2O5)及产率理论计算值与实测值的标准误差σ分别为:3.711、1.832、0.984。
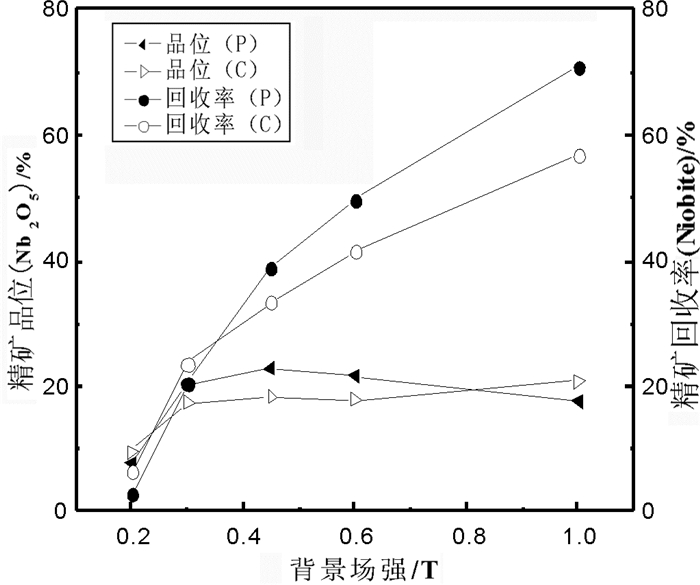 |
| 图 5 精矿回收率和品位的比较 Fig.5 Comparisons on the recovery and grade of oncentrate |
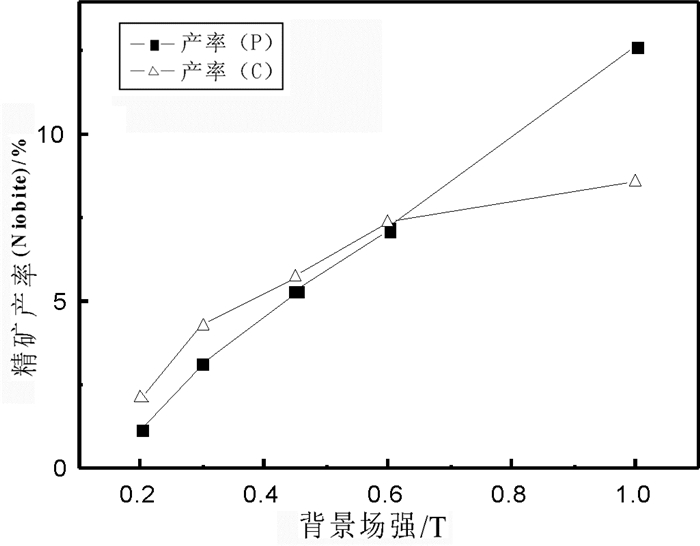 |
| 图 6 精矿的产率比较 Fig.6 A comparison on the yield of concentrate |
(1) 当背景场强较小时(0.2~0.3 T),精矿的实际产率和回收率偏低,原因在于磁场力较弱、与流体阻力相差较小,弱磁性颗粒受重力及其它因素的干扰较大, 而实际计算时对此忽略。此外,由于捕集区域偏小,部分铌铁矿在进入捕集区域前随着矿浆运动而离开磁场,使得实测值较低。
(2) 当背景场强B0在0.45~0.6 T时,精矿的产率、回收率、品位等理论值与实测值误差较少。
(3) 当背景场强B0较大时(0.6~1.0 T),精矿的实际回收率偏高,颗粒夹杂随背景场强的提高、捕集范围的增加而影响显著;当背景场强为1 T时,由于夹杂显著提高致使品位偏低。
(4) 适当增加平行于磁场方向的棒介质间距,将有利于钽铌矿分选效率的提高。
(5) “瞬时快照法”忽略矿浆流动对颗粒分选过程的影响,而颗粒所受流体拖曳力是采用阿连阻力公式计算,对磁选效率预测的精确性存在一定影响。采用复解析保角变换或其它方法对流场的影响进行深入分析,将有助于提高磁性颗粒所受流体阻力的计算精度,增强预测的准确性。
最终的试验方案是:先弱磁选(< 0.1 T)预处理去除钛铁矿,强磁选(1.0 T)富集钽铌矿,然后对矿物进行筛分去除石榴石,后降低磁场强度(0.6 T)回收钽铌精矿,最后采用摇床去除褐铁矿和赤铁矿。
5 结论通过理论计算与钽铌矿粗精矿分选实践的对比,证明采用“瞬时快照法”对磁选过程进行分析,用偏心椭圆簇对高梯度磁场中磁性颗粒捕集区域进行拟合,然后计算精矿的回收率、产率以及品位,能够对高梯度磁选效率进行预评估,从而确立合适的分选方案,并大大减少模拟试验次数。该研究方法及结果对其它弱磁性矿物的高梯度磁选实践也具有一定的指导意义和参考价值。
| [1] |
高玉德, 邹霓, 董天颂. 钽铌矿资源概况及选矿技术现状和进展[J]. 广东有色金属学报, 2004(2): 87-92. |
| [2] |
蒋海勇, 戴惠新, 杨伟林, 等. 钽铌矿精选的研究现状[J]. 矿产综合利用, 2015(5): 13-16. |
| [3] |
孙仲元, 肖金华, 陈玉, 等. 从选厂尾矿中高梯度磁选钽铌的研究[J]. 稀有金属, 1984(5): 1-6. |
| [4] |
张成强, 张红新, 李洪潮, 等. 非洲某钽铌粗精矿精选试验研究[J]. 中国矿业, 2016(3): 1211-126. |
| [5] |
徐建民. 由复势函数求场强梯度的公式[J]. 科学通报, 1982(15): 958-959. |
| [6] |
Saff E.B., Snider A.D.. Fundamentals of complex analysis with applications to engineering and science[M]. 3rd edition. New Jersey: Prentice Hall, 2003.
|
| [7] |
徐建民, 周二星, 杨守业. 齿板型聚磁介质磁场的计算[J]. 有色金属工程, 1983(3): 30-36. |
| [8] |
徐建民, 徐建成. 圆柱形多极磁选机磁场分布和场强梯度的解析计算[J]. 有色金属工程, 2001(4): 66-69. |
| [9] |
孙仲元. 磁选理论及应用[M]. 长沙: 中南大学出版社, 2009.
|
| [10] |
王亚玲, 刘应中, 缪国平. 圆柱绕流的三维数值模拟[J]. 上海交通大学学报, 2001(10): 1464-1469. DOI:10.3321/j.issn:1006-2467.2001.10.008 |
| [11] |
骆振福. 流态化分选理论[M]. 北京: 中国矿业大学出版社, 2002.
|
 2018
2018 
