2. 广西相对论天体物理重点实验室, 广西 南宁 530004;
3. 云南省中马HF-VHF先进射电天文技术国际联合实验室, 云南 昆明 650216
2. Guangxi Key Laboratory for the Relativistic Astrophysics, Nanning 530004, China;
3. Yunnan Province China-Malaysia HF-VHF Advanced Radio Astronomy Technology International Joint Laboratory, Kunming 650216, China
活动星系(Active Galactic)是一类特殊的星系,它存在猛烈的活动现象或剧烈的物理过程。活动星系的核心为活动星系核(Active Galactic Nuclei, AGN),活动星系上的现象和过程主要来自活动星系核[1]。耀变体(Blazar)是活动星系核的子类,它们的相对论带电粒子喷流几乎沿着观察者的视线(≤10°)[2]。耀变体通常分为两个子类:蝎虎座BL型天体(BL Lacertae, BL Lac)和平谱射电类星体(Flat Spectrum Radio Quasar, FSRQ)。蝎虎天体的谱线为无特征的连续谱线或非常微弱的发射谱线[3],平谱射电类星体在光学和紫外波段表现出明显的发射谱线[4]。耀变体是最多变的系外天体之一,具有大幅快速的光变和从射电到光学波段的比较高的辐射偏振[5],并且辐射主要是非热辐射[6]。准周期振荡在X射线双星中经常被检测到[7],偶尔存在于各种各样的耀变体、窄线Seyfert1(NLS1)星系,以及时间尺度在几分钟到几年不等的其他活动星系核子类中[8]。
凌日系外行星巡天卫星是美国国家航空航天局(National Aeronautics and Space Administration, NASA)于2018年发射升空的太空望远镜,主要目标是寻找围绕最亮矮星运行的系外行星[9]。凌日系外行星巡天卫星拥有4个宽视场光学电荷耦合器件(Charge-Coupled Device, CCD)相机,每个相机的视场(Field-of-View, FOV)为24°× 24°,4个相机连在一起,形成了24°× 96°的视场[9]。凌日系外行星巡天卫星将天球分为26个条状区域,称为“扇区”(Sector),南北天球各13个扇区,4个CCD相机形成的视场即为一个扇区的观测范围。凌日系外行星巡天卫星完成一个扇区的观测大约需要27天,以此类推,完成全天球的巡天大约需要两年[10]。由于凌日系外行星巡天卫星的视场为矩形,因此天球中有一些特定的区域位于多个扇区(特别是靠近两极的区域),天球赤道附近的区域会有空隙[11]。凌日系外行星巡天卫星拥有自己的数据目录,包含对目标天体光学波段的观测。凌日系外行星巡天卫星收集的数据可以从MAST(The Mikulski Archive for Space Telescopes)数据库中获得[12]。
在凌日系外行星巡天卫星数据库中,我们用时间序列分析法进行准周期信号搜索。搜索结果表明,蝎虎天体PKS 0422+004可能存在准周期振荡,因此,我们对PKS 0422+004进行进一步的分析。蝎虎天体PKS 0422+004的红移z=0.268[13],在U波段和B波段的星等分别为16.65 mag(AB)和15.94 mag(AB)[14]。
1 数据分析我们使用MAST数据库(https://archive.stsci.edu)的搜索引擎MAST Portal(https://mast.stsci.edu/portal/Mashup/Clients/Mast/Portal.html)下载耀变体PKS 0422+004的光变曲线数据,该目标源在第32扇区观测到。BTJD(TESS Barycentric Julian Day)是在数据产品中记录时间的格式,以儒略日减去2457000,并根据到达太阳系重心的时间进行校正,得到凌日系外行星巡天卫星数据的观测时间, 从而使得BTJD不受闰秒影响[10]。凌日系外行星巡天卫星第32扇区观测数据在BTJD 2173-2200之间,即27天左右,这意味着光变周期小于14天的源都可能检出。为防止以“天”为单位导致的周期数值过小,本文将横坐标BTJD乘24,转化为“小时”,使周期数值更明显。凌日系外行星巡天卫星有两种类型流量数据:简单孔径测光流量(Simple Aperture Photometry Flux, SAP_FLUX)和预研究调节简单孔径测光流量(Presearch Data-Conditioned Simple Aperture Photometry Flux, PDCSAP_FLUX)。SAP流量数据作为原始数据包含多种仪器效应,PDCSAP流量在一定程度上修正了仪器效应带来的周期信号的影响[15]。本文主要研究短时标的周期性,因此在分析该耀变体周期时使用了PDCSAP流量数据。
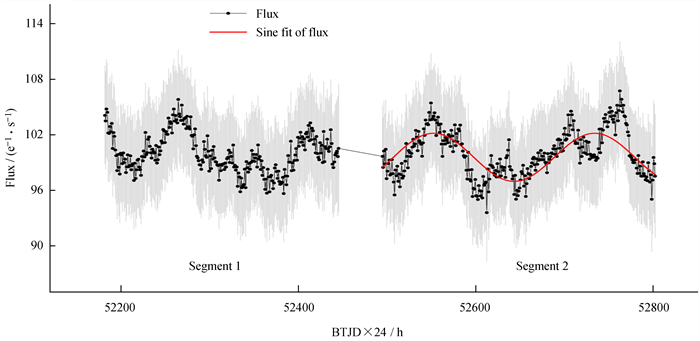
最终生成的光变曲线有一段时间的空缺,这是由于凌日系外行星巡天卫星要把观测到的数据传回地球,因此,卫星在这段时间不观测,反映在数值上为NaN(Not a Number)值。这个空缺对光变曲线造成了不均匀采样,所以我们一个扇区的整条光变曲线分成两部分(Segment),之后的分析将从第1部分开始。凌日系外行星巡天卫星每两分钟测量一次目标天体的流量[9],为更好地显示数据的分布和趋势,我们将数据分在间隔为1 h的区间内,并对区间内的时间和流量取平均值,以便之后的分析。上述处理之后的光变曲线如图 1,横坐标为时间,纵坐标为流量。为了初步判断该源是否存在准周期,我们使用origin软件的非线性拟合工具对光变曲线的中的第2部分进行正弦拟合,其拟合优度R2=0.47。
|
| 图 1 以1 h为单位分区间后的PKS 0422+004光变曲线(灰色部分为误差),红实线为第2部分流量的正弦拟合 Fig. 1 PKS 0422+004 light curve after binning in units of 1 hour (The gray part represents the error), the solid red line is the sine fitting of the flux of segment 2 |
LSP(Lomb-Scargle Periodogram)是一种用于检测时间序列数据中周期性(即使是不规则采样)的方法[16]。LSP对每个频率的数据拟合为正弦模型,若频率对应的功率较大,说明该频率极有可能存在。设σ2为方差,则LSP的公式为
| $ P(\omega)=\frac{1}{2 \sigma^2}(\text { cosine term }+ \text { sine term }), $ | (1) |
其中,余弦项(cosine term)和正弦项(sine term)分别为
| $ \text { cosine term }=\frac{\left[\sum\limits_j\left(X_j-\bar{X}\right) \cos \omega\left(t_j-\tau\right)\right]^2}{\sum\limits_j \cos ^2 \omega\left(t_j-\tau\right)}, $ | (2) |
| $ \text { sine term }=\frac{\left[\sum\limits_j\left(X_j-\bar{X}\right) \sin \omega\left(t_j-\tau\right)\right]^2}{\sum\limits_j \sin ^2 \omega\left(t_j-\tau\right)} \text {, } $ | (3) |
其中,tj为测量时间;Xj为对应的流量值;X为Xj的平均值;ω为频率;τ为对应时间t的相位修正,可以表示为
| $ \tan (2 \omega \tau)=\frac{\sum\limits_{i=1}^{N_0} \sin \left(2 \omega t_i\right)}{\sum\limits_{i=1}^{N_0} \cos \left(2 \omega t_i\right)} $ | (4) |
地面观测光学光变曲线的时间间隔通常不均匀,因此很难根据准周期振荡获得其真实频谱的准确估计,也很难估计功率谱中峰值高度的置信水平[17]。而本文使用的凌日系外行星巡天卫星光学数据的采样非常均匀,因此,不存在因为周期性采样间隔造成的虚假准周期振荡。在用蒙特卡洛方法模拟红噪声光变曲线时,设红噪声的幂律指数β=-1[18]。
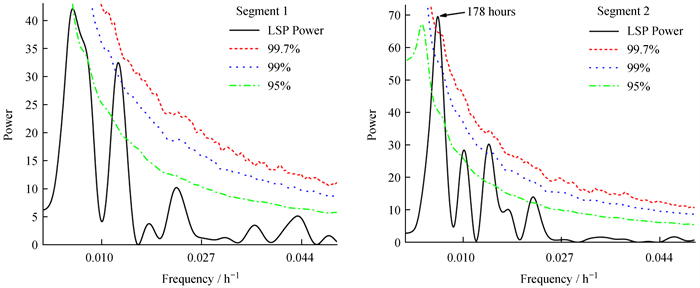
图 2为PKS 0422+004在第1和第2部分准周期振荡的蒙特卡洛置信度分析结果,其中黑线表示功率谱图,它的峰值即为准周期频率,红虚线、蓝点线和绿点划线分别为蒙特卡洛模拟的3σ(99.7%),2.6σ(99%)和2σ(95%)置信度曲线。
|
| 图 2 PKS 0422+004的光变曲线的LSP功率谱。红线、蓝线和绿线表示准周期振荡的置信度曲线 Fig. 2 LSP power spectrum of the light curve of PKS 0422+004. The red, blue, and green lines represent the confidence curves of QPO |
第1部分(Segment 1)中,PKS 0422+004没有置信度大于3σ的准周期,只有一个超过了2.6σ的峰,对应的周期为3.2天,因此,我们认为这一部分的准周期较弱。第2部分(Segment 2)中有一个178小时(约7.4天)的峰,超过了3σ置信度的准周期,因此,我们认为这一部分的准周期约为7.4天。此外,还有一个峰超过2.6σ,该峰对应的周期约为3.0天,与第1部分中3.2天的周期相近。
3 加权小波Z变换周期分析傅里叶变换为检测周期或准周期振荡提供了一种理想的工具,但是它要求振荡具有恒定的振幅和相位,而天文数据一般不具有恒定性[11]。因此,当信号表现出短的特征振荡间隔时,傅里叶变换可能不是最佳的。小波分析(Wavelet Analysis)由傅里叶变换演化而来,它可以检查描述周期信号和准周期信号的参数(周期、振幅和相位)的时间演化[19]。经过伸缩a和平移b变换将小波母函数变换为小波函数[20]:
| $ \varPsi_{a, b}(t)=\frac{1}{\sqrt{a}} \varPsi\left(\frac{t-b}{a}\right), $ | (5) |
文[21]定义了加权小波变换(WWT):
| $ W W T=\frac{\left(N_{\text {eff }}-1\right) V_y}{2 V_x}, $ | (6) |
其中,Neff为有效数据点个数;Vx为数据的加权偏差;Vy为模型函数的加权偏差。该原理在较低频率处的有效数据Neff大于在较高频率处的有效数据,所以加权小波变换的值更倾向于较高的频率处,因此,文[21]应用了Z统计量,我们称为加权小波Z变换[22]:
| $ Z=\frac{\left(N_{\text {eff }}-3\right) V_y}{2\left(V_x-V_y\right)} . $ | (7) |
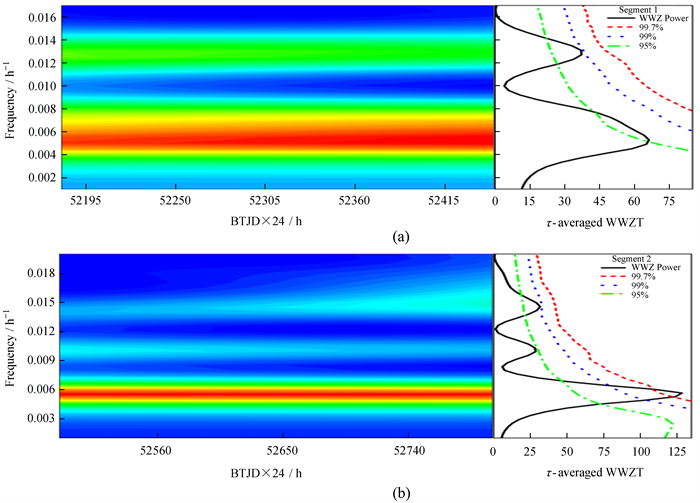
我们根据加权小波变换的原理处理PKS 0422+004的数据。图 3中黑色曲线代表周期的函数图,红虚线、蓝点线和绿点划线分别代表基于红噪声的3σ,2.6σ和2σ的置信度曲线。
|
| 图 3 PKS 0422+004的光变曲线的加权小波Z变换方法的分析结果 Fig. 3 Analysis results of weighted wavelet Z-transform method for the light curve of PKS 0422+004 |
图 3中,图(a)为PKS 0422+004的光变曲线的第1部分利用加权小波Z变换方法得到的结果。由图(a)可知,第1部分中没有置信度大于3σ的峰值,只有一个接近2.6σ的峰,对应的周期为3.2天,我们认为这一部分的准周期比较弱。图(b)为第2部分利用加权小波Z变换方法得到的结果。图(b)表明,PKS 0422+004的光变曲线第2部分的峰值178 h(约7.4天)超过3σ,我们认为这是比较可信的准周期。此外,还有一个对应周期约为3.0天的接近2.6σ的峰,与第1部分中3.2天的周期相近。
4 讨论与结论本文使用LSP方法和加权小波Z变换方法对耀变体PKS 0422+004进行分析,发现它存在一个置信度大于3σ的7.4天的准周期振荡,另外,我们在两个部分都发现了3.2天左右的准周期振荡(置信度约为2.6σ)。虽然两部分的光变曲线之间有很大数据空缺,但是我们仍对整体的光变曲线进行了周期分析,发现其中有个约6.4天的准周期振荡,刚好是3.2天的两倍。我们以7.4天为该源的主周期,而3.2天及6.4天的准周期振荡是弱的周期。
为了对耀变体天量级的准周期振荡进行解释,我们分析了此类准周期振荡的各种物理起源。此类准周期振荡可能有3种起源机制:(1)起源于吸积盘的周期性脉动[23-24];(2)起源于喷射不稳定性或螺旋运动[25];(3)起源于吸积盘与喷流的相互作用[26-27]。吸积盘中的物理过程可能导致光学和X射线中产生一些变化。与吸积盘的有限循环相关的振荡不会与开普勒或冷泽-提尔苓(Lense Thirring)调制的振荡相互作用,但与射流不稳定性或喷流中的螺旋运动相关的振荡可能受到冷泽-提尔苓进动的调制[28]。本文中7.4天的主周期,可能源于第1种物理机制,在此基础上,我们可以进一步估算该耀变体的中心黑洞质量。
活动星系核的中心黑洞质量是最为重要的一个物理量。主流的黑洞质量估计方法有恒星和气体运动学(Stellar and Gas Kinematics)法和反响映射(Reverberation Mapping)法[29],这些估算黑洞质量的方法都需要测量光谱线或热光度。由于该源没有光谱线,我们在分析时也没有它的热光度,于是我们采用文[30]提出的表达式
| $ \frac{M}{M_{\odot}}=\frac{3.23 \times 10^4 P}{\left(r^{3 / 2}+a\right)(1+z)} $ | (8) |
进行黑洞质量估计。假定周期与吸积盘内部区域附近的一些斑点或耀斑的轨道时标有关[31],其中,M⊙为太阳质量;P是以秒为单位的周期;z为红移;a为角动量参数;r为径向距离,设为最内层稳定圆轨道(Innermost Stable Circular Orbit, ISCO)。施瓦西黑洞模型中,r=6, a=0;极端克尔黑洞模型中,r=1.2, a=0.998 2[32]。因此,我们估算PKS 0422+004的黑洞质量为1.11 × 109M⊙(施瓦西黑洞)和7.07 × 109M⊙(极端克尔黑洞)。
| [1] |
黄克谅. 类星体与活动星系核[M]. 北京: 中国科学技术出版社, 2005. HUANG K L. Quasar and active galactic nuclei[M]. Beijing: China Science and Technology Press, 2005. |
| [2] | URRY C M, PADOVANI P. Unified schemes for radio-loud active galactic nuclei[J]. Publications of the Astronomical Society of the Pacific, 1995, 107(715): 803–845. |
| [3] | STOCKE J T, MORRIS S L, GIOIA I M, et al. The Einstein observatory extended medium-sensitivity survey. Ⅱ-the optical identifications[J]. The Astrophysical Journal Supplement Series, 1991, 76: 813–874. DOI: 10.1086/191582 |
| [4] | BLANDFORD R D, REES M J. Extended and compact extragalactic radio sources: interpretation and theory[J]. Physica Scripta, 1978, 17(3): 265–274. DOI: 10.1088/0031-8949/17/3/020 |
| [5] |
文一, 肖宇婷, 李孝攀, 等. 费米耀变体的射电波段周期性光变研究[J]. 天文研究与技术, 2023, 20(2): 95–102 WEN Y, XIAO Y T, LI X P, et al. Quasi-periodic variations in the radio light curves of Fermi blazars[J]. Astronomical Research & Technology, 2023, 20(2): 95–102. |
| [6] | GUPTA A C, GAUR H, WIITA P J, et al. Characterizing optical variability of OJ 287 in 2016-2017[J]. The Astronomical Journal, 2019, 157(3): 95. DOI: 10.3847/1538-3881/aafe7d |
| [7] | REMILLARD R A, MCCLINTOCK J E. X-ray properties of black-hole binaries[J]. Annual Review of Astronomy and Astrophysics, 2006, 44(1): 49–92. DOI: 10.1146/annurev.astro.44.051905.092532 |
| [8] | SANDRINELLI A, COVINO S, DOTTI M, et al. Quasi-periodicities at year-like timescales in blazars[J]. The Astronomical Journal, 2016, 151(3): 54. DOI: 10.3847/0004-6256/151/3/54 |
| [9] | RICKER G R, WINN J N, VANDERSPEK R, et al. The transiting exoplanet survey satellite[C]//Proceedings of SPIE. 2016: 767-784. |
| [10] |
唐延柯, 盖宁, 李志凯, 等. TESS空间卫星单扇区变星的周期性研究[J]. 天文学报, 2021, 62(4): 70–85 TANG Y K, GAI N, LI Z K, et al. Research on periodicity of single sector variable star of TESS space satellite[J]. Acta Astronomica Sinica, 2021, 62(4): 70–85. DOI: 10.15940/j.cnki.0001-5245.2021.04.006 |
| [11] | KISHORE S, GUPTA A C, WIITA P J. Detection of quasi-periodic oscillations in the blazar S4 0954+658 with TESS[J]. The Astrophysical Journal, 2023, 943(1): 53. DOI: 10.3847/1538-4357/aca809 |
| [12] | GINSBURG A, SIPÖCZ B M, BRASSEUR C E, et al. Astroquery: an astronomical web-querying package in Python[J]. The Astronomical Journal, 2019, 157(3): 98. DOI: 10.3847/1538-3881/aafc33 |
| [13] | SHAW M S, ROMANI R W, COTTER G, et al. Spectroscopy of the largest ever γ-ray-selected BL Lac sample[J]. The Astrophysical Journal, 2013, 764(2): 135. DOI: 10.1088/0004-637X/764/2/135 |
| [14] | MALLERY R P, RICH R M, SALIM S, et al. Keck deimos spectroscopy of a GALEX UV-selected sample from the Medium Imaging Survey[J]. The Astrophysical Journal Supplement Series, 2007, 173(2): 471–481. DOI: 10.1086/516638 |
| [15] | JENKINS J M, TWICKEN J D, MCCAULIFF S, et al. The TESS science processing operations center[C]//Proceedings of SPIE. 2016: 1232-1251. |
| [16] | LOMB N R. Least-squares frequency analysis of unequally spaced data[J]. Astrophysics and Space Science, 1976, 39(2): 447–462. DOI: 10.1007/BF00648343 |
| [17] | HORNE J H, BALIUNAS S L. A prescription for period analysis of unevenly sampled time series[J]. The Astrophysical Journal, 1986, 302: 757–763. DOI: 10.1086/164037 |
| [18] | TIMMER J, KOENIG M. On generating power law noise[J]. Astronomy and Astrophysics, 1995, 300: 707–710. |
| [19] |
陈军平, 马力, 龚云露, 等. 耀变体CGRaBS J0929+5013和J2146-1525光变相关性及准周期分析[J]. 天文研究与技术, 2022, 19(3): 189–197 CHEN J P, MA L, GONG Y L, et al. Correlation and quasi-periodic oscillation analysis of light variation in blazar CGRaBS J0929+5013 and J2146-1525[J]. Astronomical Research & Technology, 2022, 19(3): 189–197. |
| [20] | GROSSMANN A, MORLET J. Decomposition of hardy functions into square integrable wavelets of constant shape[J]. Siam Journal on Mathematical Analysis, 1984, 15(4): 723–736. DOI: 10.1137/0515056 |
| [21] | FOSTER G. Wavelets for period analysis of unevenly sampled time series[J]. The Astronomical Journal, 1996, 112(4): 1709–1729. |
| [22] | FOSTER G. Time series analysis by projection. Ⅰ. statistical properties of Fourier analysis[J]. The Astronomical Journal, 1996, 111(1): 541–554. |
| [23] | EDELSON R, NANDRA K. A cutoff in the x-ray fluctuation power density spectrum of the Seyfert 1 galaxy NGC 3516[J]. The Astrophysical Journal, 1999, 514(2): 682–690. DOI: 10.1086/306980 |
| [24] | CANNIZZO J K. Accretion disks in active galactic nuclei-vertically explicit models[J]. The Astrophysical Journal, 1992, 385: 94–107. DOI: 10.1086/170918 |
| [25] | GIOMMI P, PERRI M, CAPALBI M, et al. X-ray spectra, light curves and SEDs of blazars frequently observed by Swift[J]. Monthly Notices of the Royal Astronomical Society, 2021, 507(4): 5690–5702. DOI: 10.1093/mnras/stab2425 |
| [26] | BLANDFORD R, MEIER D, READHEAD A. Relativistic jets from active galactic nuclei[J]. Annual Review of Astronomy and Astrophysics, 2019, 57: 467–509. DOI: 10.1146/annurev-astro-081817-051948 |
| [27] | SHAKURA N I, SUNYAEV R A. Black holes in binary systems. Observational appearance[J]. Astronomy and Astrophysics, 1973, 24: 337–355. |
| [28] | THIRRING H, LENSE J. Über den Einfluss der Eigenrotation der Zentralkörperauf die Bewegung der Planeten und Monde nach der Einsteinschen Gravitationstheorie[J]. Physikalische Zeitschrift, 1918, 19(8): 156–163. |
| [29] | MCLURE R J, DUNLOP J S. On the black hole-bulge mass relation in active and inactive galaxies[J]. Monthly Notices of the Royal Astronomical Society, 2002, 331(3): 795–804. DOI: 10.1046/j.1365-8711.2002.05236.x |
| [30] | GUPTA A C, SRIVASTAVA A K, WIITA P J. Periodic oscillations in the intra-day optical light curves of the blazar S5 0716+714[J]. The Astrophysical Journal, 2009, 690(1): 216–223. DOI: 10.1088/0004-637X/690/1/216 |
| [31] | ZHANG X H, BAO G. The rotation of accretion disks and the power spectra of X-ray "flickering"[J]. Astronomy and Astrophysics, 1991, 246: 21–31. |
| [32] | ESPAILLAT C, BREGMAN J, HUGHES P, et al. Wavelet analysis of AGN X-ray time series: A QPO in 3C 273?[J]. The Astrophysical Journal, 2008, 679(1): 182–193. DOI: 10.1086/587023 |



