活动星系核(Active Galactic Nuclei, AGN)是宇宙中最高能、最致密的天体之一,它们的辐射能量来源于中央超大质量黑洞的气体/尘埃吸积过程。赛弗特星系(Seyfert Galaxy)是一种活动星系核,可以分为两个标准次型:赛弗特1型和2型星系。前者的光谱中存在宽的允许线,后者的允许线宽度和禁线宽度相差不大。在活动星系核统一模型中,两者的中心引擎结构类似,观测性质的差异来源于不同的观测视角[1]。另外,赛弗特星系还包含一个性质尤为独特的子类——窄线赛弗特1型星系(Narrow Line Seyfert 1 Galaxies, NLS1s)。它们的光谱具有相对窄的Hβ发射线线宽(半峰全宽小于2 000 km·s-1)和较弱的禁线([OIII]λ5007/Hβ < 3),强铁发射线,陡峭的X射线谱和快速大幅X射线光变[2-3]。绝大部分窄线赛弗特1型星系表现为射电宁静,仅有约7%表现为射电噪,这些源中显著的射电辐射一般认为来自相对论性喷流[4]。相对于类似光度的宽发射线赛弗特1型星系,它们具有较低的黑洞质量和较高的吸积率(接近爱丁顿极限)[5]。
费米空间望远镜(Fermi-LAT)的长时、高精度、全域巡天探测到20多个窄线赛弗特1型星系的伽马射线辐射(下文简称为GNLS1s),表明部分赛弗特星系中存在相对论性喷流结构[6-7]。它们是除耀变体(Blazar)和射电星系(Radio Galaxy)外,被发现的第3种具有伽马射线辐射的活动星系核。有观测表明,赛弗特星系的寄主星系一般为低质量旋涡星系,在这类星系中发现相对论性喷流可能挑战现有的喷流产生机制。因为主流观点认为,相对论性喷流一般起源于星系合并形成的大质量椭圆星系(例如在耀变体、射电星系中)[8-9]。相对于众多的、具有伽马射线辐射、寄主星系为椭圆星系的耀变体,GNLS1s数量稀少。观测表明,这两类源的寄主星系不同,却具有较多类似的物理性质,例如单向探测喷流、射电平谱、双峰能谱结构、高偏振、快速日内光变、喷流成分的视超光速运动等性质[6, 8]。
光变分析是探索活动星系核内部物理过程的一种重要手段。在前期工作中,我们收集整理了25个已知的GNLS1s或高置信度候选体[9]。我们利用广域红外巡天探测器的测光数据,系统搜寻了这些源的中红外波段日内光变,发现其中13个源至少在一个观测窗口表现出显著(大于3σ)的日内光变。这25个GNLS1s红移均小于1。最近,文[10]报道了一个新的伽马噪窄线赛弗特1型星系TXS 1206+549(赤经RA=12h08m54.2564s,赤纬Dec=+54d41m58.162s),光谱红移z=1.344,这是迄今为止发现的红移最大的GNLS1星系。这个源具有平的射电谱,大于100的射电噪度(即表现为射电甚噪),典型的双峰能谱结构,存在多波段光变。他们利用文[11]的σm参数(误差修正的内禀光变幅度)粗略研究了这个源的中红外波段日内光变,在共14组天量级光变曲线中,计算了TXS 1206+549的3.4 μm和4.6 μm波段光变幅度σm,采用σm > 0的标准,计算了3.4 μm和4.6 μm波段的日内光变占空系数,结果分别为91%和79%,表明这个源在天量级时标上活动性极强。
本文聚焦研究TXS 1206+549的中红外波段日内光变,主要考虑如下几点:
(1) WISE最近释放了新的观测数据,测光数据延伸到2022年12月13日,本文将最新的WISE观测数据加入日内光变分析中。文[10]是基于14组天量级光变曲线展开研究,本文则包括21组天量级光变曲线。特别地,我们注意到TXS 1206+549在MJD≈59698(2022年4月29日)处于所有WISE观测窗口中的最亮阶段,3.4 μm和4.6 μm波段星等分别达到12.7 mag和11.6 mag。在这个观测窗口,TXS 1206+549表现出显著的日内光变,这是首次报道TXS 1206+549中确认的中红外波段日内光变现象。
(2) 由于红移大、距离远,在大部分WISE观测窗口,TXS 1206+549处于较“暗”水平。对于这种“暗”源,观测星等的误差较大。因此,类似于前期工作[9],我们采用3种统计方法相结合的方式仔细搜寻TXS 1206+549每条天量级光变曲线中大于3σ的日内光变。相对于文[10]仅基于光变幅度σm>0的标准,我们选择的光变标准更严格,可信度更高。
(3) 作为前期工作的补充[3, 9], 本文还系统研究了TXS 1206+549的短时标和长时标颜色变化,探讨了不同时标上光变机制的差异。
1 WISE光变曲线广域红外巡天探测器是美国航空航天局在2009年12月发射的空间望远镜,任务为在红外波段绘制整个天空的图像[12]。WISE搭载了一台40 cm口径的红外望远镜,工作在3.4 μm, 4.6 μm, 12 μm和22 μm波段(分别称为W1, W2, W3和W4波段),空间分辨率为6.1″, 6.4″, 6.5″和12″。WISE每6个月完成一次全天区巡天任务。在大约1天时间内,探测器绕其轨道运行15次,因而可以得到目标源包含多个测光数据点(典型值12个)的天量级光变曲线[13]。相比红外天文卫星(Infrared Astronomical Satellite, IRAS),WISE的灵敏度提高了100倍左右,给天文学家提供了前所未有的机遇来研究活动星系核的红外性质[14]。
利用美国航空航天局红外科学数据库(NASA/IPAC Infrared Science Archive)和3″搜索半径,我们获取了TXS 1206+549(它的WISE对应体的名称为WISE J120854.25+544158.2)在2010年5月至2022年12月的W1和W2波段所有原始测光数据。首先,我们对数据进行了必要的筛选,剔除不良数据,采用的标准为nb=1, na=0, moon_masked=‘00’, cc_flags=‘00’, w1sat=0, w2sat=0, w1snr≥7, w2snr≥5, w1rchi2 < 10, w2rchi2 < 10, qual_frame > 0, qi_fact > 0, saa_sep > 0, sso_flag=0。另外,还剔除了W1或W2星等仅为上限的数据点。测光数据质量的详情可参考官方文档。最后得到了TXS 1206+549的W1和W2波段同时性光变曲线,共21个观测窗口(Epoch),309组W1和W2测光数据(见图 1和表 1展示的部分数据)。每个观测窗口平均包含15组测光数据,平均观测时长约1.28天(见表 2的第2、第3列)。
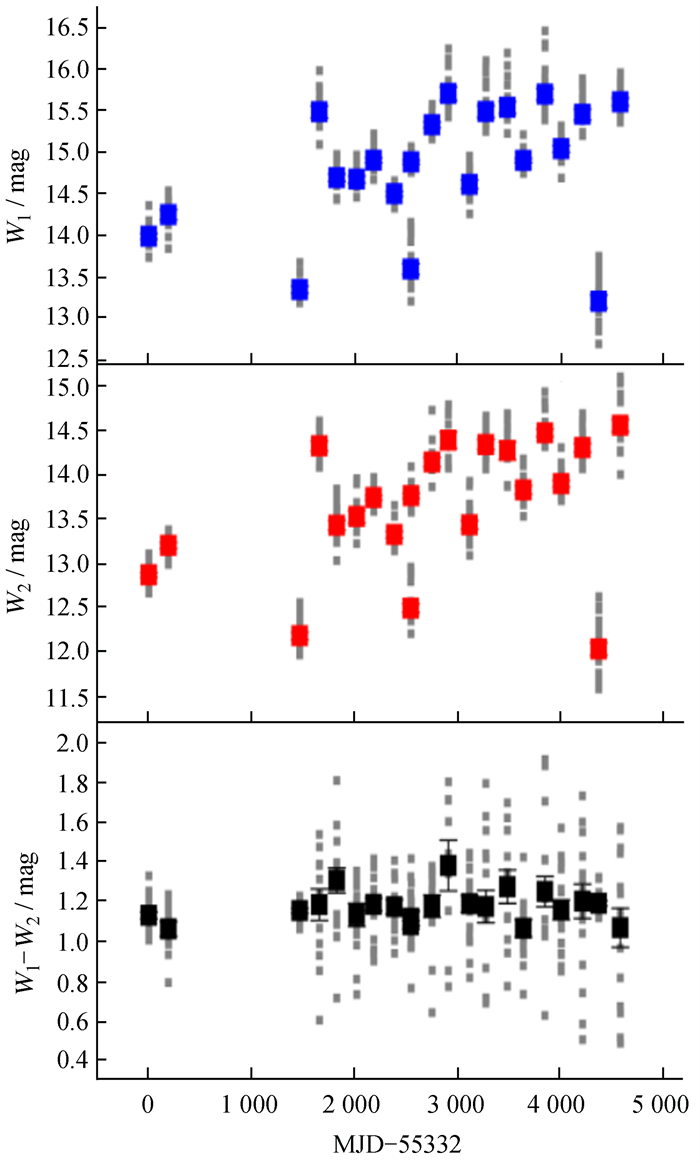
|
| 图 1 W1和W2波段光变曲线以及颜色W1-W2的长期变化。灰色小方形表示每个观测窗口的数据;蓝色、红色、黑色大方形分别表示每个观测窗口的平均W1星等、平均W2星等、平均颜色W1-W2 Fig. 1 The light curves on W1 and W2 bands, and the long-term variality of color index W1-W2. The grey small squares represent the data of every observational epoch; the blue, red and black big squares are the average W1 magnitudes, W2 magnitudes, and color indices W1-W2 during individual observational epoch, respectively |
| Epoch (1) |
MJD (2) |
W1/mag (3) |
e_W1/mag (4) |
SNR1 (5) |
w1rchi2 (6) |
W2/mag (7) |
e_W2/mag (8) |
SNR2 (9) |
w2rchi2 (10) |
| 1 | 55332.741073 | 14.094 | 0.057 | 19.1 | 1.04E+00 | 12.904 | 0.059 | 18.4 | 1.45E+00 |
| 55332.873377 | 14.364 | 0.062 | 17.6 | 1.49E+00 | 13.111 | 0.060 | 18.1 | 1.27E+00 | |
| 55333.005681 | 14.049 | 0.063 | 17.3 | 4.55E-01 | 12.894 | 0.058 | 18.7 | 1.25E+00 | |
| 55333.137858 | 13.913 | 0.049 | 22.1 | 1.28E+00 | 12.788 | 0.049 | 22.0 | 6.88E-01 | |
| 55333.137985 | 13.998 | 0.051 | 21.4 | 1.86E+00 | 12.891 | 0.058 | 18.7 | 2.51E+00 | |
| 55333.204073 | 14.071 | 0.050 | 21.9 | 1.14E+00 | 12.925 | 0.056 | 19.5 | 1.19E+00 | |
| 55333.270162 | 14.122 | 0.057 | 19.0 | 1.07E+00 | 12.924 | 0.054 | 20.3 | 1.15E+00 | |
| 55333.270289 | 13.965 | 0.051 | 21.4 | 1.33E+00 | 12.936 | 0.058 | 18.8 | 1.59E+00 | |
| 55333.336377 | 14.107 | 0.051 | 21.2 | 1.45E+00 | 12.961 | 0.062 | 17.5 | 6.86E-01 | |
| 55333.402593 | 14.068 | 0.058 | 18.7 | 9.60E-01 | 13.034 | 0.062 | 17.4 | 8.65E-01 | |
| 55333.468681 | 14.180 | 0.061 | 17.9 | 9.43E-01 | 12.851 | 0.054 | 20.1 | 1.44E+00 | |
| 55333.534770 | 13.940 | 0.054 | 20.2 | 1.30E+00 | 12.842 | 0.051 | 21.2 | 1.43E+00 | |
| 55333.534897 | 14.078 | 0.058 | 18.7 | 2.49E+00 | 12.955 | 0.058 | 18.7 | 1.61E+00 | |
| 55333.600985 | 13.994 | 0.047 | 22.9 | 1.89E+00 | 12.807 | 0.056 | 19.5 | 1.40E+00 | |
| 55333.667074 | 13.875 | 0.051 | 21.3 | 6.87E-01 | 12.785 | 0.051 | 21.4 | 9.10E-01 | |
| 55333.667201 | 13.988 | 0.054 | 20.1 | 1.42E+00 | 12.915 | 0.054 | 20.2 | 1.00E+00 | |
| 55333.733289 | 13.746 | 0.042 | 25.9 | 1.13E+00 | 12.691 | 0.053 | 20.7 | 1.16E+00 | |
| 55333.865593 | 13.976 | 0.052 | 20.9 | 1.26E+00 | 12.734 | 0.056 | 19.4 | 4.09E-01 | |
| 55333.997897 | 14.071 | 0.052 | 21.0 | 1.35E+00 | 13.065 | 0.065 | 16.7 | 9.94E-01 | |
| 55334.130201 | 13.737 | 0.042 | 25.7 | 1.64E+00 | 12.663 | 0.049 | 22.3 | 6.84E-01 | |
| 注:表 1只列出了首个观测窗口的测光数据,完整表 1存储在国家天文科学数据中心(NADC),可点击http://paperdata.china-vo.org/MLS/TXS1206.csv直接下载。 | |||||||||
| Epoch (1) |
ΔT (2) |
N (3) |
W1/mag (4) |
W2/mag (5) |
W1-W2/mag (6) |
| 1 | 1.39 | 20 | 13.991±0.033 | 12.870±0.026 | 1.130±0.018 |
| 2 | 1.26 | 14 | 14.251±0.061 | 13.203±0.036 | 1.062±0.037 |
| 3 | 1.38 | 16 | 13.352±0.043 | 12.181±0.043 | 1.154±0.012 |
| 4 | 1.12 | 12 | 15.488±0.072 | 14.330±0.058 | 1.184±0.079 |
| 5 | 1.38 | 16 | 14.697±0.045 | 13.432±0.056 | 1.306±0.063 |
| 6 | 1.11 | 11 | 14.677±0.041 | 13.531±0.070 | 1.132±0.058 |
| 7 | 1.38 | 18 | 14.905±0.031 | 13.745±0.025 | 1.185±0.033 |
| 8 | 1.24 | 13 | 14.504±0.029 | 13.328±0.039 | 1.174±0.036 |
| 9 | 1.24 | 16 | 13.598±0.066 | 12.494±0.048 | 1.083±0.021 |
| 10 | 1.24 | 15 | 14.885±0.023 | 13.767±0.029 | 1.115±0.036 |
| 11 | 1.11 | 11 | 15.331±0.033 | 14.148±0.053 | 1.177±0.056 |
| 12 | 1.37 | 9 | 15.707±0.081 | 14.395±0.090 | 1.381±0.127 |
| 13 | 1.24 | 17 | 14.616±0.054 | 13.437±0.049 | 1.188±0.042 |
| 14 | 1.37 | 14 | 15.492±0.071 | 14.345±0.058 | 1.175±0.082 |
| 15 | 1.24 | 11 | 15.540±0.072 | 14.278±0.102 | 1.274±0.084 |
| 16 | 1.24 | 15 | 14.903±0.025 | 13.832±0.048 | 1.065±0.044 |
| 17 | 1.37 | 14 | 15.699±0.069 | 14.478±0.042 | 1.250±0.076 |
| 18 | 1.37 | 18 | 15.045±0.040 | 13.902±0.038 | 1.158±0.050 |
| 19 | 1.24 | 15 | 15.457±0.066 | 14.310±0.049 | 1.201±0.087 |
| 20 | 1.37 | 18 | 13.210±0.078 | 12.033±0.072 | 1.191±0.013 |
| 21 | 1.24 | 16 | 15.608±0.044 | 14.563±0.070 | 1.068±0.098 |
表 1给出了详细的W1和W2波段测光数据。第1列为观测窗口序号;第2列为简化儒略日期MJD;第3列为W1星等;第4列为W1星等误差;第5列为W1波段的仪器轮廓拟合测光信噪比SNR1;第6列为W1波段的仪器轮廓拟合测光简化卡方值;第7至第10列类似第3至第6列,描述的是W2波段。表 2给出了每个观测窗口的时长(第2列,单位为天)、测光点个数(第3列)、平均W1星等(第4列)、平均W2星等(第5列)和平均色指数W1-W2(第6列)。
2 日内光变分析对于每条天量级W1和W2波段光变曲线,联合3种统计方法判断是否表现出日内光变。
2.1 参数V文[15]定义了衡量光变概率的参数V,广泛用于各种光变研究中。参数V由光变曲线的卡方值导出:
| $ \chi^2=\sum\limits_{i=1}^{N_{\mathrm{ob}}} \frac{\left(m_i-\bar{m}\right)^2}{\sigma_{\mathrm{err}, i}^2} $ | (1) |
其中,mi为星等;σerr, i为星等误差;m为平均星等;Nob为数据点个数。
| $ V=-\log \left[1-\Gamma\left(\frac{N_{\mathrm{ob}}-1}{2}, \frac{\chi^2}{2}\right)\right], $ | (2) |
其中,Γ为不完全伽马函数。V值越大,光变的概率越高。文献中常采用的标准为V > 1.3,即光变概率高于95%。所有参数V的计算结果展示在表 3的第2和第3列中。
| Epoch (1) |
V[3.4] (2) |
V[4.6] (3) |
Δ[3.4] (4) |
Δ[4.6] (5) |
| 1 | 21.4 | 9.3 | >0 | >0 |
| 2 | 30.7 | 4.6 | >0 | >0 |
| 3 | >100 | >100 | >0 | >0 |
| 4 | 2.5 | 0.3 | >0 | < 0 |
| 5 | 8.7 | 8.5 | >0 | >0 |
| 6 | 3.2 | 5.1 | >0 | >0 |
| 7 | 2.0 | 0.1 | >0 | < 0 |
| 8 | 2.0 | 2.2 | >0 | >0 |
| 9 | >100 | 36.2 | >0 | >0 |
| 10 | 0.2 | 0.2 | < 0 | < 0 |
| 11 | 0.2 | 0.3 | < 0 | < 0 |
| 12 | 1.2 | 0.6 | >0 | < 0 |
| 13 | 19.1 | 7.5 | >0 | >0 |
| 14 | 3.6 | 0.4 | >0 | < 0 |
| 15 | 1.9 | 1.9 | >0 | >0 |
| 16 | 0.4 | 1.7 | < 0 | >0 |
| 17 | 1.8 | 0 | >0 | < 0 |
| 18 | 3.1 | 0.5 | >0 | < 0 |
| 19 | 3.7 | 0.2 | >0 | < 0 |
| 20 | >100 | >100 | >0 | >0 |
| 21 | 0.4 | 0.5 | < 0 | < 0 |
标准额外方差σNXV2常用来衡量光变幅度,“额外”表示从总方差中去除观测误差带来的方差[16]。具体定义为
| $ \sigma_{\mathrm{NXV}}^2=\frac{1}{N_{\mathrm{ob}} \bar{y}^2} \sum\limits_{i=1}^{N_{\mathrm{ob}}}\left[\left(y_i-\bar{y}\right)^2-\sigma_{\mathrm{err}, i}^2\right], $ | (3) |
σNXV2的误差为
| $ \operatorname{err}\left(\sigma_{\mathrm{NXV}}^2\right)=\frac{S_{\mathrm{D}}}{\bar{y}^2 N_{\mathrm{ob}}^{1 / 2}}, $ | (4) |
| $ S_{\mathrm{D}}^2=\frac{1}{N_{\mathrm{ob}}} \sum\limits_{i=1}^{N_{\mathrm{ob}}}\left\{\left[\left(y_i-\bar{y}\right)^2-\sigma_{\mathrm{err}, i}^2\right]-\sigma_{\mathrm{NXV}}^2 \bar{y}^2\right\}^2, $ | (5) |
误差较大时,err(σNXV2)可能大于σNXV2。参考文[16],定义Δ=σNXV2-err(σNXV2)。如果Δ > 0,表明误差修正的内禀光变幅度大于0。所有参数Δ的计算结果展示在表 3的第4和第5列中。
2.3 光变显著性在[X]波段(X=3.4,4.6分别表示W1波段,W2波段)的第i条天量级光变曲线,按
| $ \varPhi[X]^i=\sqrt{\frac{1}{N_{\mathrm{ob}}-1} \sum\limits_{j=1}^{N_{\mathrm{ob}}}\left(m[X]_j^i-\overline{m[X]^i}\right)^2} $ | (6) |
计算标准偏差,其中,
WISE的巡天视场为47′ × 47′。我们利用一个更大的搜索范围60′ × 60′,获取TXS 1206+549附近所有的源,限定与第i条天量级光变曲线有类似的观测时段(即MJD范围)和测光点个数后,计算所有剩余源的平均[X]波段星等,最后挑出200个最接近TXS 1206+549在此时的平均[X]波段星等的源。对于挑出的200个源的同时段光变曲线,按照(6)式同样计算光变标准偏差。它们的平均值记作Φ′[X]i,标准偏差记作ε′[X]。类似文[17],按
| $ \sigma[X]=\frac{\varPhi[X]^i-\varPhi^{\prime}[X]^i}{\varepsilon^{\prime}[X]} $ | (7) |
估算第i条[X]波段天量级光变曲线的光变置信度,σ[X]>3表示置信度达到3σ的日内光变。表 4展示了光变置信度估计的结果。
| Epoch (1) |
Φ [3.4]i (2) |
Φ′[3.4]±ε′[3.4] (3) |
σ [3.4] (4) |
Φ [4.6] (5) |
Φ′[4.6]±ε′[4.6] (6) |
σ [4.6] (7) |
Epoch (1) |
Φ [3.4]i (2) |
Φ′[3.4]±ε′[3.4] (3) |
σ [3.4] (4) |
Φ [4.6] (5) |
Φ′[4.6]±ε′[4.6] (6) |
σ [4.6] (7) |
|
| 1 | 0.14 | 0.07±0.02 | >3 | 0.12 | 0.08±0.02 | < 3 | 12 | 0.30 | 0.33±0.11 | < 3 | 0.28 | 0.38±0.10 | < 3 | |
| 2 | 0.21 | 0.08±0.02 | >3 | 0.13 | 0.11±0.03 | < 3 | 13 | 0.23 | 0.11±0.03 | >3 | 0.22 | 0.14±0.05 | < 3 | |
| 3 | 0.18 | 0.05±0.01 | >3 | 0.18 | 0.05±0.02 | >3 | 14 | 0.33 | 0.25±0.05 | < 3 | 0.22 | 0.28±0.08 | < 3 | |
| 4 | 0.27 | 0.22±0.07 | < 3 | 0.21 | 0.25±0.07 | < 3 | 15 | 0.33 | 0.28±0.11 | < 3 | 0.33 | 0.28±0.09 | < 3 | |
| 5 | 0.18 | 0.12±0.04 | < 3 | 0.23 | 0.13±0.04 | < 3 | 16 | 0.12 | 0.14±0.03 | < 3 | 0.19 | 0.18±0.06 | < 3 | |
| 6 | 0.15 | 0.11±0.04 | < 3 | 0.26 | 0.15±0.06 | < 3 | 17 | 0.35 | 0.26±0.07 | < 3 | 0.20 | 0.30±0.07 | < 3 | |
| 7 | 0.14 | 0.13±0.03 | < 3 | 0.12 | 0.17±0.05 | < 3 | 18 | 0.16 | 0.15±0.04 | < 3 | 0.18 | 0.19±0.05 | < 3 | |
| 8 | 0.10 | 0.10±0.03 | < 3 | 0.15 | 0.12±0.04 | < 3 | 19 | 0.27 | 0.21±0.06 | < 3 | 0.21 | 0.26±0.07 | < 3 | |
| 9 | 0.31 | 0.06±0.02 | >3 | 0.25 | 0.08±0.03 | >3 | 20 | 0.33 | 0.04±0.01 | >3 | 0.32 | 0.05±0.02 | >3 | |
| 10 | 0.10 | 0.13±0.03 | < 3 | 0.13 | 0.18±0.06 | < 3 | 21 | 0.19 | 0.24±0.06 | < 3 | 0.34 | 0.30±0.07 | < 3 | |
| 11 | 0.13 | 0.19±0.06 | < 3 | 0.23 | 0.23±0.08 | < 3 |
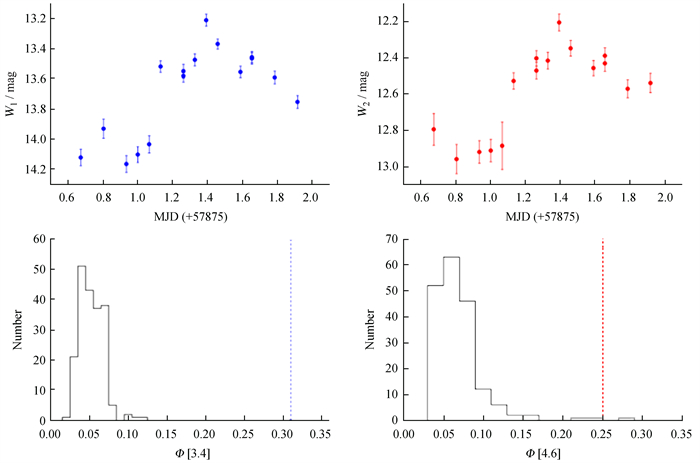
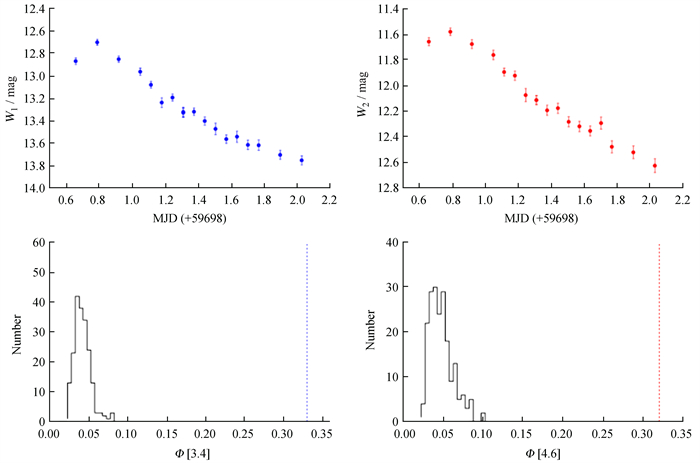
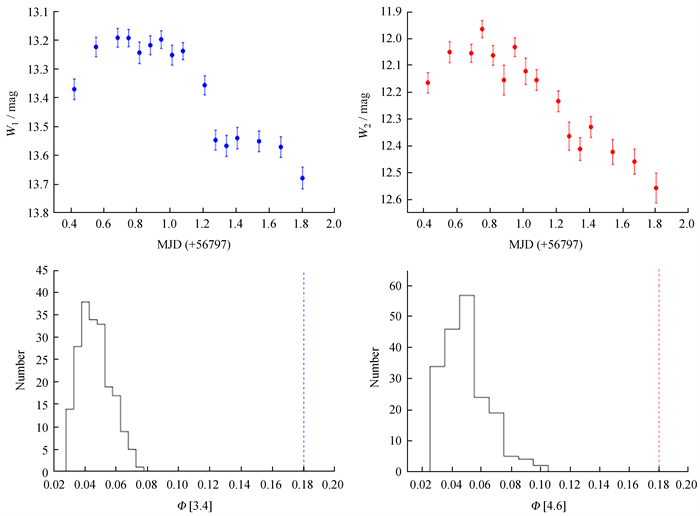
与前期工作相同,我们联合上述3个统计量判定是否表现出日内光变:V[X]>1.3 & Δ[X]>0 & σ[X]>3,即同时满足上述关系时,认为在[X]波段表现出大于3σ的显著日内光变。在TXS 1206+549的21个WISE观测窗口中,有3个窗口W1波段和W2波段均表现出显著的日内光变:窗口3(MJD 56797.42153~56798.8034,见图 2)、窗口9(MJD 57875.67271~57876.91668,见图 3)和窗口20(MJD 59698.65573~59700.0264,见图 4)。
|
| 图 2 观测窗口3(Epoch 3)的W1和W2波段日内光变(上部两子图)。200个类似亮度WISE源的W1和W2波段光变标准偏差分布(下部两子图),其中蓝色和红色竖直虚线表示TXS 1206+549的W1和W2波段光变标准偏差 Fig. 2 IDVs of W1 and W2 bands during Epoch 3 (upper two panels). The bottom two panels show the histograms of Φ[3.4] and Φ[4.6] of the 200 field sources with the most similar brightness. The vertical dashed lines indicate the Φ[3.4] (blue) and Φ[4.6] (red) for TXS 1206+549 |
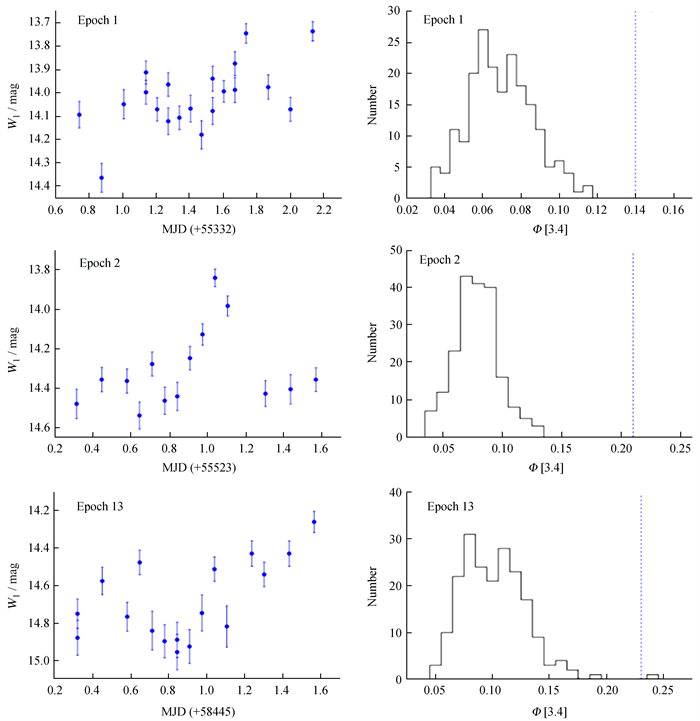
特别地,TXS 1206+549在观测窗口20,即2022年4月29日,达到所有观测窗口的最亮水平,表现出非常特殊的光变过程:在约1.24天内,W1和W2波段分别持续变暗约1.1 mag和1.0 mag。线性拟合光变曲线表明:在W1和W2波段的变暗率分别为0.91 mag·day-1和0.88 mag·day-1。两个波段的光变曲线高度类似,W1与W2星等之间的斯皮尔曼相关系数Rs=0.97。据文献调研,这是首次报道关于TXS 1206+549高置信度的中红外波段日内光变。另外,TXS 1206+549在3个观测窗口仅在W1波段表现出大于3σ的显著光变(见图 5):窗口1(MJD 55332.74107~55334.1302)、窗口2(MJD 55523.31162~55524.56819)和窗口13(MJD 58445.31964~58446.56296)。文[18]给出计算光变占空系数的方法为
| $ D C=100 \times \frac{\sum\limits_{i=1}^M A_i\left(1 / \Delta T_i\right)}{\sum\limits_{i=1}^M\left(1 / \Delta T_i\right)} \%, $ | (8) |
其中,ΔTi=ΔTi, ob/(1 + z);ΔTi, ob为光变曲线时长;z为红移。当第i条天量级光变曲线表现出显著度大于3σ的日内光变时,Ai取1,否则Ai取0。(8)式给出TXS 1206+549在W1和W2波段的占空系数分别为27.8%和13.7%,明显小于文[10]报道的占空系数(91%和79%)。这显然是由于我们采用了更为保守、更为严格的光变标准(大于3σ),而文[10]仅要求σm > 0,这个标准类似Δ > 0。
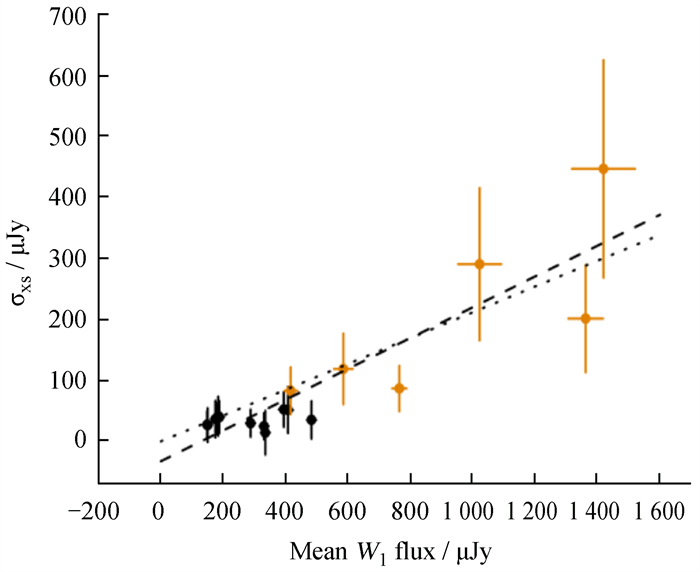
另外,联合所有观测窗口,我们研究了流量方均根-流量(rms-flux)关系。首先,将W1星等转换为流量,单位为μJy。然后,计算每个观测窗口的W1波段平均流量及误差,方法见文[3]的公式(1)和(2)。剩余均方根(excess rms),记作σXS,常用来衡量光变曲线中剔除误差影响后的内禀光变。根据文[19],
| $ \sigma_{\mathrm{XS}}=\sqrt{S^2-\bar{\sigma}_{\mathrm{err}}^2}, $ | (9) |
其中,S2为样本方差;
| $ \begin{aligned} \sigma_{\mathrm{XS}}= & (0.25 \pm 0.03) \bar{f}+ \\ & (-32.53 \pm 20.30) \end{aligned} $ | (10) |
|
| 图 6 光变均方根-流量(rms-flux)关系。橘色点对应表现出3σ光变的6个观测窗口。黑色虚线和点线分别为不固定和固定截距的最佳线性拟合线 Fig. 6 The rms-flux correlation. Orange points indicate six epochs showing 3σ variabilities. The dashed line is the best-fitting straight line for these points, and the dotted line is the best-fitting straight line when forcing intercept of 0 |
黑色点线表示截距固定为0时的线性拟合结果,
| $ \sigma_{\mathrm{XS}}=(0.21 \pm 0.02) \bar{f} $ | (11) |
利用WISE研究红外颜色变化的优势体现在W1和W2两个波段的观测是同时性的。为进一步了解TXS 1206+549的颜色变化,我们构建了长期和短期颜色-星等图,W1星等作为横坐标,颜色W1-W2作为纵坐标,采用斯皮尔曼相关系数Rs描述两者之间的相关性。同时,采用加权最小二乘法,拟合了颜色-星等散点图:(W1-W2)=AW1+B,A为斜率,B为截距,拟合时考虑颜色和星等的误差。类似文[3],表征颜色变化趋势为A > 0, Rs > 0.5, p < 0.05时,源表现出变亮变蓝的趋势;A < 0, Rs < -0.5, p < 0.05时,源表现出变亮变红的趋势。
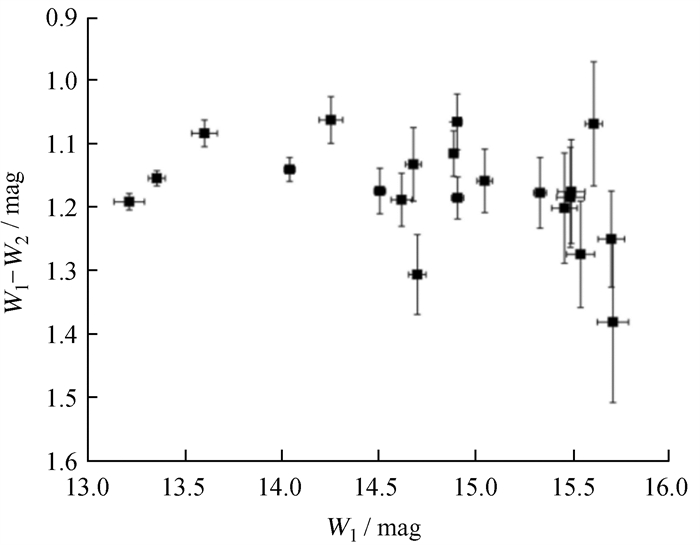
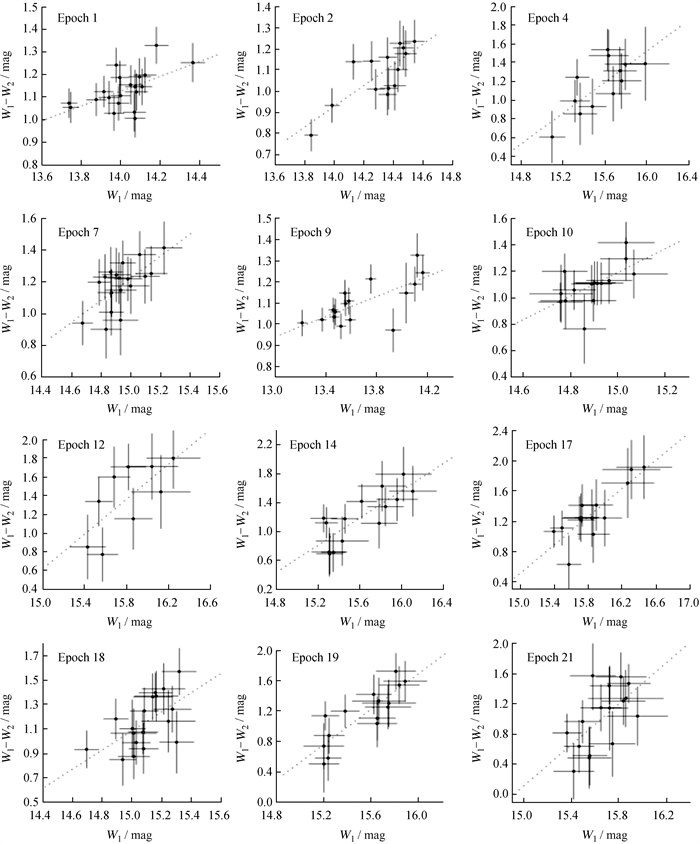
图 7给出了窗口平均后的长期颜色-星等图。对于21个观测窗口,Rs=0.39,p=0.04。这说明在长时标上,TXS 1206+549未表现出显著的颜色变化趋势,即表现为准消色差(Quasi-achromatic)。表 5给出了每个观测窗口的颜色-星等图分析结果。21个观测窗口中,有12个表现出变亮变蓝的趋势,剩余窗口未表现出明显的颜色变化趋势。图 8给出了12个表现出变亮变蓝的趋势的颜色-星等图和线性拟合结果。对于6个表现出3σ光变的窗口来说,3个表现出变亮变蓝的趋势。
|
| 图 7 观测窗口平均后的(W1-W2)~W1关系 Fig. 7 The correlaiton between the epoch-averaged W1-W2 and W1 |
| Epoch (1) |
N (2) |
Slope (3) |
Rs (4) |
Prob. (5) |
Note (6) |
| 1 | 20 | 0.31±0.12 | 0.56 | 5.4E-03 | BWB |
| 2 | 14 | 0.51±0.12 | 0.76 | 7.2E-04 | BWB |
| 3 | 16 | -0.01±0.08 | -0.15 | 2.9E-01 | — |
| 4 | 12 | 0.80±0.34 | 0.60 | 2.1E-02 | BWB |
| 5 | 16 | 0.72±0.21 | 0.40 | 6.9E-02 | — |
| 6 | 11 | 0.01±0.30 | -0.19 | 3.0E-01 | — |
| 7 | 18 | 0.70±0.28 | 0.56 | 8.9E-03 | BWB |
| 8 | 13 | 0.34±0.32 | 0.25 | 2.2E-01 | — |
| 9 | 16 | 0.25±0.07 | 0.63 | 4.5E-03 | BWB |
| 10 | 15 | 0.83±0.43 | 0.69 | 2.2E-03 | BWB |
| 11 | 11 | 0.41±0.61 | 0.52 | 5.7E-02 | — |
| 12 | 9 | 0.96±0.41 | 0.70 | 2.0E-02 | BWB |
| 13 | 17 | 0.39±0.14 | 0.46 | 3.5E-02 | — |
| 14 | 14 | 0.78±0.26 | 0.72 | 1.6E-03 | BWB |
| 15 | 11 | 0.20±0.34 | 0.48 | 7.4E-02 | — |
| 16 | 15 | 0.23±0.45 | 0.17 | 2.9E-01 | — |
| 17 | 14 | 0.80±0.30 | 0.78 | 3.8E-04 | BWB |
| 18 | 18 | 0.80±0.28 | 0.63 | 2.7E-03 | BWB |
| 19 | 15 | 1.03±0.27 | 0.84 | 1.7E-05 | BWB |
| 20 | 18 | 0.05±0.04 | 0.16 | 2.7E-01 | — |
| 21 | 16 | 1.38±0.45 | 0.60 | 7.9E-03 | BWB |
|
| 图 8 12个观测窗口的源变亮颜色变蓝现象 Fig. 8 Bluer-when-brighter during 12 epochs |
利用WISE巡天数据,系统研究了目前已知的最遥远的伽马噪窄线赛弗特1型星系TXS 1206+549的中红外波段光变性质,主要结论如下:
(1) TXS 1206+549在2022年4月29日达到所有观测窗口的最亮水平,在约1.24天内W1和W2波段分别持续变暗约1.1 mag和1.0 mag。这是首次报道TXS 1206+549高置信度的中红外波段日内光变。
(2) 联合3种统计方法研究了TXS 1206+549的日内光变,得出W1和W2波段的光变占空系数分别为27.8%和13.7%。
(3) TXS 1206+549的中红外波段光变存在显著的均方根-流量线性关系。
(4) 长期来看,TXS 1206+549未表现出显著的红外颜色变化,在天量级时标上却普遍表现出变亮变蓝的趋势。
快速光变可用来限定辐射区域的尺寸。假设辐射区域为半径R的球状体,利用因果关系可以估
计R的大小:R≤cτ(1+z)-1,c为光速;τ保守取1天;z=1.344。对于TXS 1206+549而言,R≤3.4 × 10-4 pc。如果考虑多普勒效应且多普勒因子δ取典型值10,则R≤3.4 × 10-3 pc。活动星系核的红外辐射可能有多种起源[22],可能是喷流中的同步辐射、尘埃环热辐射、恒星形成过程辐射的混合模式。在TXS 1206+549中发现显著的中红外日内光变可以排除(至少在这些观测窗口)辐射由尘埃环辐射主导的可能性,因为一般认为尘埃环距离中心0.01~0.1 pc。文[13]最早利用WISE数据发现两个GNLS1s的红外日内光变(PMN J0948+0022, SBS 0846+513),他们认为红外波段日内光变揭示红外辐射由喷流中相对论性电子的同步辐射主导。
文[10]利用σm参数研究了TXS 1206+549的中红外波段日内光变。采用σm > 0的标准,计算了W1和W2波段的占空系数,结果分别为91%和79%。本文联合3种统计方法,我们得出TXS 1206+549在W1和W2波段的占空系数分别为27.8%和13.7%,显著低于文[10]的相应值。3种方法中的Δ > 0类似于σm > 0。如果仅选择Δ > 0作为日内光变标准,W1和W2波段的占空系数分别为79.9%和52.3%,接近但仍低于文[10]的占空系数。显然,我们联合3种统计方法给出的占空系数值显著低的原因是由于仅挑选置信度大于3σ的日内光变,这个标准更为严格,但给出的日内光变可靠度也更高。
从图 1可看出长时标上TXS 1206+549的W1和W2波段亮度变化幅度大:在所有观测窗口里(2010年5月至2022年12月),W1波段星等变化了约3.76 mag,W2波段星等变化了约3.53 mag。另一方面,红外颜色(W1-W2)却未发生显著的变化(见图 1和图 7)。联合这两个观测事实,我们认为TXS 1206+549的长期红外光变可用观测视角变化导致多普勒因子变化的简单机制来解释[23]。文[9]系统研究了GNLS1s在天量级时标上的红外颜色变化,发现变亮变蓝的趋势普遍存在。本文发现TXS 1206+549同样在大部分观测窗口表现出变亮变蓝的趋势。GNLS1s的日内光变能用喷流中的激波传播来解释,同时激波能引起依赖频率的短时标光变,从而导致变亮变蓝的趋势[9, 24-25]。联合所有观测窗口,我们发现TXS 1206+549的中红外波段光变存在显著的均方根-流量线性相关。这表明在各种流量水平状态下(低态与高态)的光变是有关联性的[26-27],当源处于高态时光变更剧烈。
致谢: 本文利用了广域红外巡天探测器提供的巡天数据。该项目由加州理工学院喷气推进实验室和亚利桑那大学联合执行,美国航空航天局(NASA)提供资金支持。
| [1] | URRY C M, PADOVANI P. Unified schemes for radio-loud active galactic nuclei[J]. Publications of the Astronomical Society of the Pacific, 1995, 107(715): 803–845. |
| [2] | OSTERBROCK D E, POGGE R W. The spectra of narrow-line Seyfert 1 galaxies[J]. The Astrophysical Journal, 1985, 297(1): 166–176. |
| [3] |
毛李胜. 伽马噪窄线赛弗特1型星系的长期红外光变和颜色变化[J]. 天文研究与技术, 2021, 18(2): 162–172 MAO L S. The long-term infrared brightness and color variabilities of γ-ray-loud narrow-line Seyfert 1 galaxies[J]. Astronomical Research & Technology, 2021, 18(2): 162–172. |
| [4] | YUAN W, ZHOU H Y, KOMOSSA S, et al. A population of radio-loud narrow-line Seyfert 1 galaxies with blazar-like properties?[J]. The Astrophysical Journal, 2008, 685(2): 801–827. DOI: 10.1086/591046 |
| [5] | COLLIN S, KAWAGUCHI T. Super-eddington accretion rates in narrow line Seyfert 1 galaxies[J]. Astronomy and Astrophysics, 2004, 426: 797–808. DOI: 10.1051/0004-6361:20040528 |
| [6] | PALIYA V S. Gamma-ray emitting narrow-line Seyfert 1 galaxies: past, present, and future[J]. Journal of Astrophysics and Astronomy, 2019, 40(5): 39. DOI: 10.1007/s12036-019-9604-3 |
| [7] | AJELLO M, ANGIONI R, AXELSSON M, et al. The fourth catalog of active galactic nuclei detected by the Fermi large area telescope[J]. The Astrophysical Journal, 2020, 892(2): 105. DOI: 10.3847/1538-4357/ab791e |
| [8] | D'AMMANDO F. Relativistic jets in gamma-ray-emitting narrow-line Seyfert 1 galaxies[J]. Galaxies, 2019, 7(4): 87. DOI: 10.3390/galaxies7040087 |
| [9] | MAO L S, YI T F. A search for rapid mid-infrared variability in gamma-ray-emitting narrow-line Seyfert 1 galaxies[J]. The Astrophysical Journal Supplement Series, 2021, 255(1): 10. DOI: 10.3847/1538-4365/abfd3b |
| [10] | RAKSHIT S, SCHRAMM M, STALIN C S, et al. TXS 1206+549:a new γ-ray-detected narrow-line Seyfert 1 galaxy at redshift 1.34?[J]. Monthly Notices of the Royal Astronomical Society, 2021, 501(1): 22–27. |
| [11] | SESAR B, IVEZIC Z, LUPTON R H, et al. Exploring the variable sky with the sloan digital sky survey[J]. The Astronomical Journal, 2007, 134(6): 2236–2251. DOI: 10.1086/521819 |
| [12] | WRIGHT E L, EISENHARDT P R M, MAINZER A K, et al. The Wide-field Infrared Survey Explorer (WISE): mission description and initial on-orbit performance[J]. The Astronomical Journal, 2010, 140(6): 1868–1881. DOI: 10.1088/0004-6256/140/6/1868 |
| [13] | JIANG N, ZHOU H, HO L C, et al. Rapid infrared variability of three radio-loud narrow-line Seyfert 1 galaxies: a view from the wide-field infrared survey explorer[J]. The Astrophysical Journal Letters, 2012, 759(2): 31. DOI: 10.1088/2041-8205/759/2/L31 |
| [14] | ASSEF R J, STERN D, NOIROT G, et al. The WISE AGN catalog[J]. The Astrophysical Journal Supplement, 2018, 234: 23. DOI: 10.3847/1538-4365/aaa00a |
| [15] | MCLAUGHLIN M A, MATTOX J R, CORDES J M, et al. Variability of CGRO/EGRET gamma-ray sources[J]. The Astrophysical Journal, 1996, 473: 763–772. DOI: 10.1086/178188 |
| [16] | SANCHEZ P, LIRA P, CARTIER R, et al. Near-infrared variability of obscured and unobscured X-ray-selected AGNs in the COSMOS field[J]. The Astrophysical Journal, 2017, 849(2): 110. DOI: 10.3847/1538-4357/aa9188 |
| [17] | KOZLOWSKI S, KOCHANEK C S, STERN D, et al. Mid-infrared variability from the spitzer deep wide-field survey[J]. The Astrophysical Journal, 2010, 716(1): 530–543. DOI: 10.1088/0004-637X/716/1/530 |
| [18] | ROMETO G E, CELLONE S A, COMBI J A. Optical microvariability of southern AGNs[J]. Astronomy and Astrophysics Supplement, 1999, 135: 477–486. DOI: 10.1051/aas:1999184 |
| [19] | VAUGHAN S, EDELSON R, WARWICK R S, et al. On characterizing the variability properties of X-ray light curves from active galaxies[J]. Monthly Notices of the Royal Astronomical Society, 2003, 345(4): 1271–1284. DOI: 10.1046/j.1365-2966.2003.07042.x |
| [20] | BHATTACHARYYA S, GHOSH R, CHATTERJEE R, et al. Blazar variability: a study of non-stationarity and the flux-rms relation[J]. The Astrophysical Journal, 2020, 897(1): 25. DOI: 10.3847/1538-4357/ab91a8 |
| [21] | BACHEV R, TRIPATHI T, GUPTA A C, et al. Intra-night optical flux and polarization variability of BL Lacertae during its 2020-2021 high state[J]. Monthly Notices of the Royal Astronomical Society, 2023, 522(2): 3018–3035. DOI: 10.1093/mnras/stad1063 |
| [22] | CACCIANIGA A, ANTON S, BALLO L, et al. WISE colours and star formation in the host galaxies of radio-loud narrow-line Seyfert 1[J]. Monthly Notices of the Royal Astronomical Society, 2015, 451(2): 1795–1805. DOI: 10.1093/mnras/stv939 |
| [23] | RAITERI C M, VILLATA M, ACOSTA-PULIDO J A, et al. Blazar spectral variability as explained by a twisted inhomogeneous jet[J]. Nature, 2017, 552(7685): 374–377. DOI: 10.1038/nature24623 |
| [24] | MARSCHER A P, GEAR W K. Models for high-frequency radio outbursts in extragalactic sources, with application to the early 1983 millimeter-to-infrared flare of 3C 273[J]. The Astrophysical Journal, 1985, 298: 114–127. DOI: 10.1086/163592 |
| [25] | RANI B, GUPTA A C, STRIGACHEV A, et al. Short-term flux and colour variations in low-energy peaked blazars[J]. Monthly Notices of the Royal Astronomical Society, 2010, 404(4): 1992–2017. |
| [26] | BHATTA G. Characterizing long-term optical variability properties of γ-ray-bright blazars[J]. The Astrophysical Journal, 2021, 923(1): 7. DOI: 10.3847/1538-4357/ac2819 |
| [27] | UTTLEY P, MCHARDY I M, VAUGHAN S, et al. Non-linear X-ray variability in X-ray binaries and active galaxies[J]. Monthly Notices of the Royal Astronomical Society, 2005, 359(1): 345–362. DOI: 10.1111/j.1365-2966.2005.08886.x |