2. 中国科学院射电天文重点实验室, 江苏 南京 210033;
3. 新疆射电天体物理重点实验室, 新疆 乌鲁木齐 830011;
4. 新疆大学物理科学与技术学院, 新疆 乌鲁木齐 830046;
5. 中国科学院大学, 北京 100049;
6. 西华师范大学物理与天文学院, 四川 南充 637002
2. Key Laboratory of Radio Astronomy, Chinese Academy of Sciences, Nanjing 210033, China;
3. Xinjiang Key Laboratory of Radio Astrophysics, Urumqi 830011, China;
4. School of Physics and Technology, Xinjiang University, Urumqi 830046, China;
5. University of Chinese Academy of Sciences, Beijing 100049, China;
6. School of Physics and Astronomy, China West Normal University, Nanchong 637002, China
射电望远镜口径越大、观测频段越高,对指向精度的要求也越高[1-2]。天线工作于野外山地,指向精度不可避免地受到台址风扰影响[3-4]。对于大口径、高指向精度射电望远镜而言,风扰影响天线指向精度的问题已不可忽视[5]。天线罩、控制补偿等传统调控手段已无法满足当前大型射电望远镜抗风需求[6]。在不同领域的抗风工程中,风障的应用十分广泛[7-8]。在物料堆场,常利用防风网进行防风抑尘[9];大风区的道路桥梁,常通过在路基两侧搭建挡风墙等设施来保障车辆的行驶安全[10];沙漠地区常利用沙障抵挡风沙的侵蚀[11]。风障是一种具有一定开孔率或者完全不透风的障碍物,对风可以产生一定的阻碍作用,从而改变风向并消耗风能,使得障后的风速衰减。利用风障调控风场一定程度上可以改善台址的风环境。
目前,针对风障调控风场的研究主要集中在风障孔隙率、高度、面形等参量对挡风效率的影响方面[12-14]。由于布设风障领域的地形通常相对比较平坦,研究中对地形的关注度比较小。而大口径、高精度射电望远镜台址大多位于山谷或盆地内[15-17],地形相对复杂,风的流场结构也与其他领域的情况有所不同。文[18]研究了不同山丘地形的风场绕流分布,结果表明高宽比较大的山丘背风面绕流稳定性比较差,易发生流动分离;山丘越高,顶部加速比越大,下游的尾流恢复距离越长。文[19]利用风洞试验和数值模拟方法研究了某山地地形的风场特性,指出山地风速、风向变化剧烈,山脊位置的风速比在1.6~2.8之间,山谷位置的风速比在0.12~1.6之间。文[20]基于缩比模型开展了山地环境的风洞实验,研究山地背风面的尾流分布特征,研究结果表明,山体下游的流场结构与背风坡面角度有关。
为研究山地环境中地形对大口径射电望远镜台址风场调控的影响,本文以奇台射电望远镜台址地形为研究对象,利用数值模拟方法开展不同地形对风场调控影响的研究。以天线位置为中心划分核心区域,核心区域的两端分别设置风障,在核心区域的南北方向分别设置3组不同地形的边界。为了比较台址斜坡地形对风场调控的影响,构建台址水平地形对照组,通过开展不同地形工况的风场仿真研究掌握地形对风场调控的影响关系,为风障优化布局提供参考。
1 数值模拟数学模型 1.1 湍流控制方程本文采用雷诺平均(Reynolds Average Navier-Stokes, RANS) 数值模拟方法进行仿真。对于野外小区域风场仿真,可以将空气假设为低速、不可压的粘性牛顿流体。风的流动遵循质量守恒和动量守恒定律,控制方程为
| $ \frac{\partial \rho}{\partial t}+\frac{\partial}{\partial x_i}\left(\rho u_i\right)=0, $ | (1) |
| $ \frac{\partial\left(\rho u_i\right)}{\partial t}+\frac{\partial}{\partial x_i}\left(\rho u_i u_j\right)=-\frac{\partial p}{\partial x_i}+\frac{\partial}{\partial x_i}\left[\mu\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}-\frac{2}{3} \delta_{i j} \frac{\partial u_i}{\partial x_j}\right)\right]+\frac{\partial}{\partial x_i}\left(-\rho \overline{u_i^{\prime} u_j^{\prime}}\right)+S_i, $ | (2) |
其中,ρ为空气密度;t为时间;xi为沿i方向的坐标;ui为i方向的速度;p为压力;μ为流体粘度;δij为Kronecker函数;
雷诺方程本身并不封闭,需要引入湍流模型进行求解,研究采用与实际流动物理过程更加符合、求解精度更高的可实现k-ε模型,其湍动能k和耗散率ε的输运方程为
| $ \rho \frac{\partial k}{\partial t}=\frac{\partial}{\partial x_i}\left[\left(\mu+\frac{\mu_t}{\sigma_k}\right) \frac{\partial k}{\partial x_i}\right]+G_{\mathrm{k}}+G_{\mathrm{b}}-\rho \varepsilon-Y_{\mathrm{M}}, $ | (3) |
| $ \rho \frac{\partial \varepsilon}{\partial t}=\frac{\partial}{\partial x_i}\left[\left(\mu+\frac{\mu_t}{\sigma_{\varepsilon}}\right) \frac{\partial \varepsilon}{\partial x_i}\right]+\rho C_1 S \varepsilon-\rho C_2 \frac{\varepsilon^2}{k+\sqrt{v \varepsilon}}+C_{1 \varepsilon} \frac{\varepsilon}{k} C_{3 \varepsilon} G_{\mathrm{b}}, $ | (4) |
其中,σk为湍动能k的湍流普朗特数;
本文的风障具有一定的孔隙,可以看作多孔介质,仿真建模可以采用多孔跳跃模型。模型构建原理是在动量方程中增加动量源项。该源项由黏性损失项和惯性损失项两部分组成,方程为
| $ S_i=-\left(\frac{\mu}{\alpha} u_i+C_2 \frac{1}{2} \rho|u| u_i\right), $ | (5) |
其中,α为渗透率;C2为惯性阻力系数;u为流体速度。仿真中改变渗透率α对仿真结果的影响极小,该参量可以设置为常数。惯性阻力系数C2可以采用经验公式
| $ C_2=\frac{K}{\Delta n}, $ | (6) |
| $ K=\frac{1-\beta}{\beta} $ | (7) |
计算[21-22],其中,K为压力损失系数;β为风障的孔隙率;Δn为风障的厚度。本文中风障孔隙率设置为33%,风障厚度设置为0.001 6 m。
1.3 大气边界层边界条件大气边界层内,风速随高度变化的规律可以采用对数律或指数律数学公式描述。计算域入口风速采用更适用于工程计算的指数律公式表达:
| $ V(z)=V_0\left(\frac{z}{z_0}\right)^a, $ | (8) |
台址地貌类型属于B类粗糙度,a指数取0.15;z为海拔高度;z0取10 m;V0取15 m/s。
计算域入口湍流强度采用日本建筑规范中Ⅱ类地貌的湍流强度经验公式
| $ I_{(z)}=\left\{\begin{array}{c} 0.23, z \leqslant 5 \\ 0.1\left(\frac{z}{z_g}\right)^{-0.2}, 5<z<z_g \end{array}, \right. $ | (9) |
zg取350 m。计算域入口处湍动能k和湍流耗散率ε按照
| $ k=\frac{3}{2}\left[V_{(z)} I_{(z)}\right]^2, $ | (10) |
| $ \varepsilon=0.09^{\frac{3}{4}} \frac{k^{\frac{3}{2}}}{L} $ | (11) |
设置,其中,L为湍流积分尺度,取0.07倍的计算域顶高。
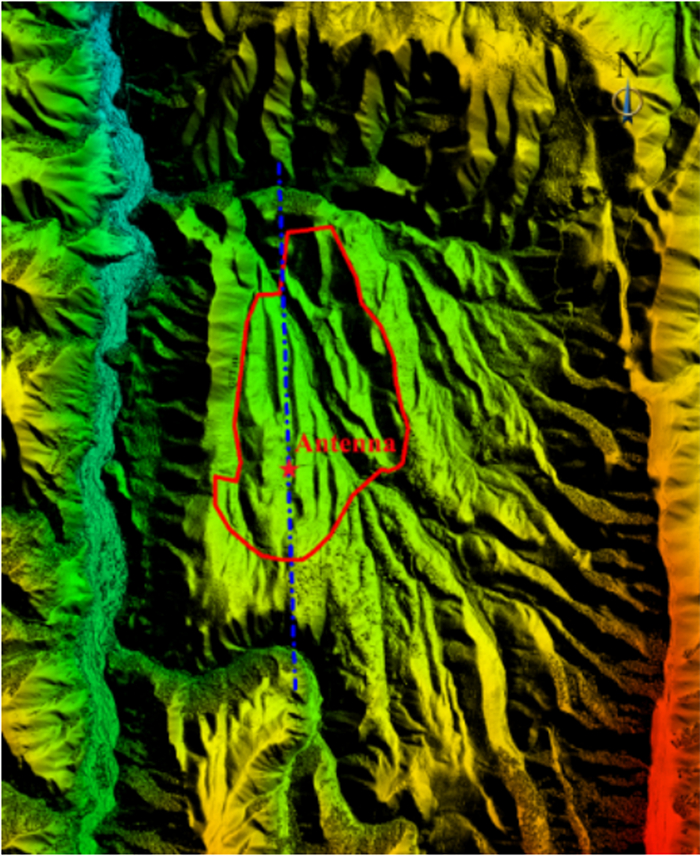
2 风场仿真与结果分析 2.1 奇台射电望远镜台址计算域模型构建奇台射电望远镜台址位于一处四面环山的矩形盆地内,地理坐标为43 °36′4.03″N,89 °40′56.99″E,海拔约为1 760 m,台址地形如图 1。台址园区内的来风主要在南北方向,东西方向来风较少[23]。因此,本文主要围绕南北方向的地形对台址风场调控产生的影响开展仿真研究。
|
| 图 1 奇台射电望远镜台址地形 Fig. 1 The terrain of the QTT site |
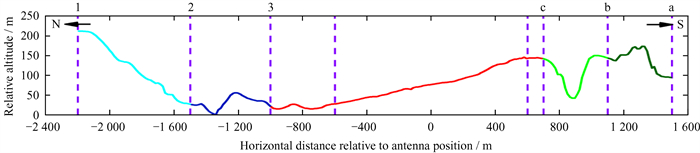
风场调控数值模拟可以采用二维或三维仿真,针对单一变量的研究采用二维仿真优势更为明显[7-9, 11, 13, 24]。本文采用二维仿真,沿天线所在点的南北方向提取台址地形高程数据,如图 2。以天线位置为中心,将水平方向-600~600 m的区域划分为核心区域,以核心区域为中心分别向北向南延伸。向北延伸的端点编号为1, 2, 3;向南延伸的端点编号为a, b, c。将2组边界端点分别进行组合,共产生9组地形模型(1a, 1b, 1c, …, 3a, 3b, 3c)。以地形模型为基础构建台址风场仿真计算域模型,计算域模型如图 3。在有风障的工况中,分别在水平方向-600 m和600 m的位置设置风障,风障高度设置为120 m。计算域模型顶高设置为3 000 m。为了保障所有仿真计算域入口风速相同,台址实际地形以外做了水平缓冲和地形缓冲。水平缓冲相对天线位置的高度和长度在所有仿真计算域模型中相同。来风条件设置为南方向来风和北方向来风。
|
| 图 2 台址地形高程数据 Fig. 2 Terrain elevation data of the site |
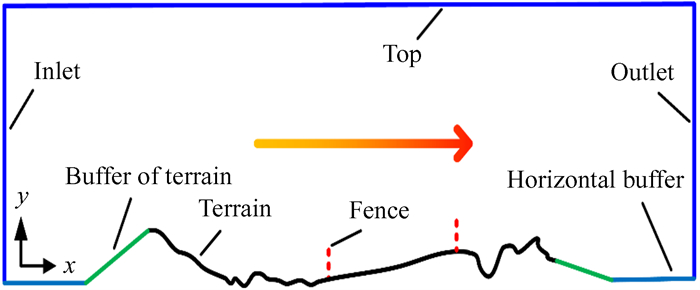
|
| 图 3 仿真计算域 Fig. 3 Computational domain of simulation |
各工况仿真结果提取相同位置的风速数据。竖直方向上,提取相对地面yr=60 m (0.5倍的风障高度)、96 m (0.8倍的风障高度) 高度的数据;水平方向上,从-600~600 m,每隔50 m提取一个数据点。风障的风速折减系数采用
| $ \lambda=\left(1-\left|\frac{V_{\mathrm{n}}}{V_{\mathrm{e}}}\right|\right) \times 100 \% $ | (12) |
计算,其中,λ为风速折减系数;Ve为无风障工况风速;Vn为有风障工况风速。
台址实际斜坡地形顺风向的风速折减系数分布如图 4。由图 4可以看出,北方向来风,顺风向风速折减系数从-600 m位置的风障后先增大,然后减小,在600 m位置的风障前再次增大;南方向来风,顺风向风速折减系数从600 m位置的风障后近似持续增加。上游边界同起点的3组地形工况,风速折减系数曲线变化更为接近,如图 4 (a)中上游起点为“1”的3组数据。由于下游边界不同,曲线之间略有差值。由此说明上游边界地形对风速折减系数的影响大于下游边界地形的影响。天线位置(水平0点) 的气流相比于风障位置更加稳定,提取天线位置相对地面yr=96 m高度处在有风障工况和无风障工况的风速以及各工况的风速折减系数如表 1。为了精确比较不同上下游边界地形对风场调控的影响,制作地形工况1c, 2c, 3c, 3b, 3a在有风障工况和无风障工况的顺风向风场流线图,如图 5和图 6。

|
| 图 4 台址斜坡地形顺风向风速折减系数分布 Fig. 4 Distribution of reducing wind speed coefficients downwind on the slope terrain of the site |
| Wind from north | Wind form south | |||||||
| Terrain number | Wind speed without wind barrier/(m/s) | Wind speed with wind barrier/(m/s) | Reducing wind speed coefficient/(%) | Terrain number | Wind speed without wind barrier/(m/s) | Wind speed with wind barrier/(m/s) | Reducing wind speed coefficient/(%) | |
| 3c | 24.02 | 11.75 | 51.08 | 1c | 23.65 | 1.67 | 92.94 | |
| 3b | 23.80 | 11.89 | 50.03 | 3c | 23.98 | 1.72 | 92.82 | |
| 3a | 23.61 | 11.88 | 49.68 | 2c | 23.90 | 1.77 | 92.61 | |
| 2c | 23.84 | 12.19 | 48.85 | 1b | 23.27 | 2.93 | 87.42 | |
| 2b | 23.60 | 12.32 | 47.76 | 3b | 23.67 | 3.09 | 86.95 | |
| 2a | 23.40 | 12.33 | 47.31 | 2b | 23.54 | 3.11 | 86.79 | |
| 1c | 23.63 | 13.62 | 42.37 | 1a | 22.24 | 3.51 | 84.22 | |
| 1b | 23.38 | 13.75 | 41.18 | 3a | 22.66 | 3.70 | 83.65 | |
| 1a | 23.17 | 13.75 | 40.65 | 2a | 22.59 | 3.74 | 83.46 | |

|
| 图 5 北方向来风台址实际斜坡地形顺风向风场流线 Fig. 5 Downwind wind flow streamline on the slope terrain of the site with northward wind |

|
| 图 6 南方向来风台址实际斜坡地形顺风向风场流线 Fig. 6 Downwind wind flow streamline on the slope terrain of the site with southward wind |
结合图 4、图 5以及表 1分析北方向来风边界地形对风场调控的影响。上游边界不同、下游边界相同地形的比较(地形1c, 2c和3c),在无风障工况中上游边界内最高点的海拔高度越高,到达天线位置的风速越小。1c地形上游最高海拔212 m,天线位置的风速为23.63 m/s;3c地形上游最高海拔28 m,天线位置的风速为24.02 m/s。在有风障工况中上游边界内最高点的海拔高度越高,经风障调控到达天线位置的风速反而越大,1c地形天线位置的风速为13.62 m/s,3c地形天线位置的风速为11.75 m/s。结合风场流线图分析认为,无风障工况中,上游山体越高,对风的遮挡能力越强;而有风障工况中,风障在天线位置削弱风速的大小与进入核心区域的风攻角呈正相关(无风障时-600 m位置的风攻角),1c, 2c和3c进入核心区域的风攻角分别为2.28 °,2.73 °和3.09 °。下游边界不同、上游边界相同地形的比较(地形3c, 3b和3a),无风障工况中,天线位置的风速同样与下游边界内最高点的海拔高度呈负相关。有风障工况中,3c地形下游边界的地形遮挡最小,但由于风出口处发生了流动分离,产生回流,对风的流动形成阻碍(如图 5 “3c-N-F”),使得天线位置的风速最小。3b地形在风出口处未发生流动分离,且地形阻碍比3a小,在天线位置的风速最大。
结合图 4、图 6以及表 1分析南方向来风边界地形对风场调控的影响。无风障工况中,天线位置的风速均与上下游边界内最高点的海拔高度呈负相关。有风障工况上游边界不同、下游边界相同地形的比较(地形3c, 3b和3a),3组地形在600 m位置的入流风攻角相近,但由于斜坡地形和风障的共同作用,天线位置发生了流动分离,被回流旋涡覆盖。从风场流线图中明显可以看出,上游风速越大,旋涡的范围越大,而天线位置的风速与入流风速成正比。图 4 (c)中上游起点为“c”的3组数据在0点下游风速折减系数开始下降,而图 4 (d)中风速折减系数则继续增强,从风场流线图中可以看出(图 6中,有风障工况3c, 2c, 1c地形),旋涡中心更接近地面96 m高度的位置,风速相对更小。而地面60 m高度距离旋涡中心更远,风速相对较大,且从0点开始,下游回流速度明显增强,因此风速折减系数降低。有风障工况中,上游边界相同、下游边界不同地形的比较(地形3c, 2c和1c),3组地形仿真结果天线位置的风速差值很小,但同样受回流旋涡位置的影响。回流旋涡形成的位置和范围受风障自身参量、斜坡地形、下游边界地形耦合作用影响。
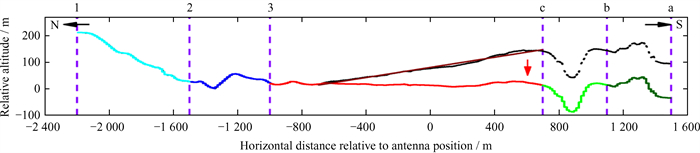
2.3 台址水平地形构建及仿真结果分析核心区域属于斜坡地形,处于迎风坡与背风坡时的风场结构明显不同,风障调控风场的效果差异也很大。由于斜坡地形的影响,图 4中,北方向来风,南边边界属于风场下游,3组下游边界地形最高点海拔落差相对较小,但对风速折减系数影响的差异明显。而南方向来风,北边边界3组地形最高点的海拔落差相对较大,但对风速折减系数影响的差异反而相对不明显。为了比较斜坡地形对风场流动的主导影响以及明确不同边界地形对核心区域风场调控的影响关系,将原有斜坡地形构建为相对水平的地形进行风场仿真研究,如图 7。仿真计算域模型构建与2.1节相同。
|
| 图 7 台址水平地形构建 Fig. 7 Constructing horizontal terrain of the site |
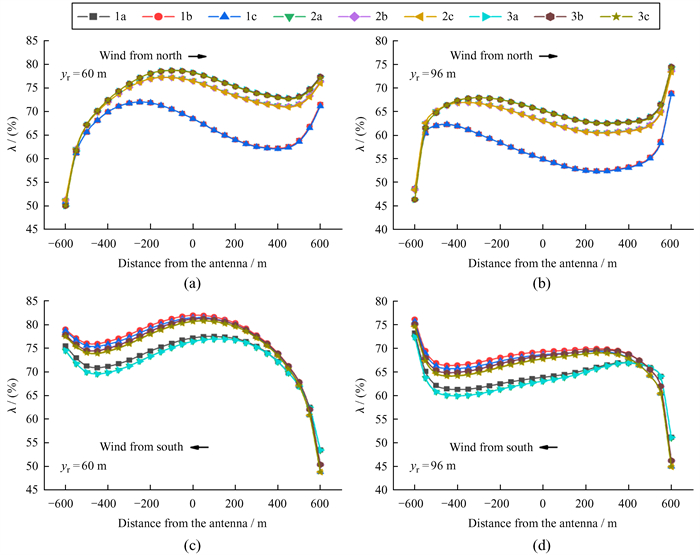
台址水平地形顺风向的风速折减系数分布如图 8。由图 8可以看出,台址斜坡地形“变”水平后,北方向来风和南方向来风的风速折减系数变化趋势相同,均为先增大再减小,然后增大。提取天线位置相对地面yr=96 m高度处在有风障工况和无风障工况的风速以及各工况的风速折减系数如表 2。制作地形工况1c, 2c, 3c, 3b和3a在有风障工况和无风障工况的顺风向风场流线图,如图 9和图 10。
|
| 图 8 台址水平地形顺风向风速折减系数分布 Fig. 8 Distribution of reducing wind speed coefficients downwind on the horizontal terrain of the site |
| Wind from north | Wind form south | |||||||
| Terrain number | Wind speed without wind barrier/(m/s) | Wind speed with wind barrier/(m/s) | Reducing wind speed coefficient/(%) | Terrain number | Wind speed without wind barrier/(m/s) | Wind speed with wind barrier/(m/s) | Reducing wind speed coefficient/(%) | |
| 3a | 22.40 | 7.78 | 65.26 | 1b | 21.99 | 6.75 | 69.31 | |
| 3b | 22.46 | 7.81 | 65.21 | 1c | 22.04 | 6.90 | 68.68 | |
| 3c | 22.46 | 7.82 | 65.19 | 2b | 22.23 | 7.01 | 68.45 | |
| 2a | 22.25 | 8.21 | 63.09 | 3b | 22.31 | 7.05 | 68.39 | |
| 2b | 22.31 | 8.24 | 63.05 | 2c | 22.26 | 7.17 | 67.80 | |
| 2c | 22.31 | 8.25 | 63.03 | 3c | 22.33 | 7.20 | 67.73 | |
| 1a | 22.09 | 9.96 | 54.93 | 1a | 21.18 | 7.65 | 63.88 | |
| 1b | 22.16 | 9.99 | 54.92 | 2a | 21.45 | 7.92 | 63.07 | |
| 1c | 22.16 | 9.99 | 54.90 | 3a | 21.54 | 7.96 | 63.05 | |
|
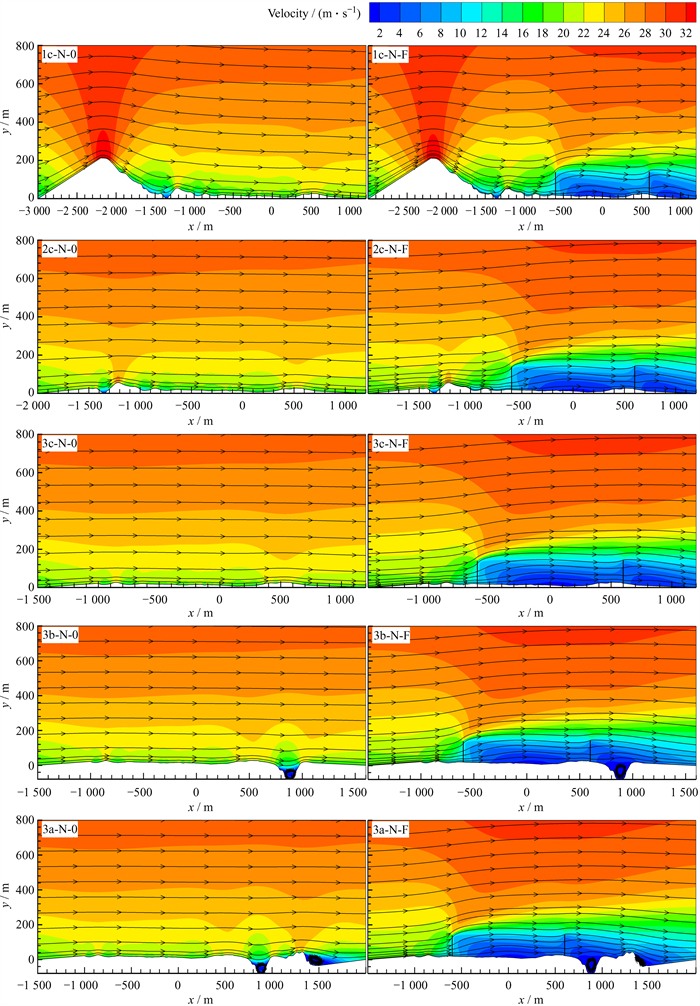
| 图 9 北方向来风台址水平地形顺风向风场流线 Fig. 9 Downwind wind flow streamline on the horizontal terrain of the site with northward wind |

|
| 图 10 南方向来风台址水平地形顺风向风场流线 Fig. 10 Downwind wind flow streamline on the horizontal terrain of the site with southward wind |
根据图 8和表 2,无风障工况中,天线位置的风速均与上下游边界地形最高点的海拔有关,上下游边界地形最高点海拔越高,天线位置的风速越小。结合图 8、图 9以及表 2分析北方向来风边界地形对风场调控的影响。有风障工况上游边界不同、下游边界相同地形的比较(地形1c, 2c和3c),风障在天线位置削弱风速的大小同样与进入核心区域的风攻角呈正相关。上游边界相同、下游边界不同的3组地形(地形3c, 3b和3a),下游边界最高点高程差很小,对天线位置削弱风速的影响差异也很小,调控后天线位置的风速分别为7.82 m/s,7.81 m/s和7.78 m/s。
结合图 8、图 10以及表 2分析南方向来风边界地形对风场调控的影响。有风障工况上游边界不同、下游边界相同地形的比较(地形3c, 3b和3a),由于没有斜坡地形的影响,风场调控后天线位置处的风速表现出与入流风攻角的相关性。3c, 3b和3a地形的入流风攻角分别为1.62 °,2.18 °和1.43 °,天线位置的风速分别为7.20 m/s, 7.05 m/s和7.96 m/s,风攻角越大,调控后的风速越小。有风障工况上游边界相同、下游边界不同地形的比较(地形1c, 2c和3c),由于下游没有回流旋涡,下游边界地形对天线位置风场调控的影响主要表现在地形对流速的阻碍上,下游边界最高点海拔越高,风场调控后天线位置的风速越小。
2.4 讨论对于目标区域相对水平的地形工况,风障遮蔽区降低风速的大小主要受上游入流风攻角的影响,入流风攻角越大,风障遮蔽区降低的风速值越大。另外,下游地形海拔越高,对风流的阻碍越大,风障遮蔽区降低风速的值也越大。如果下游地形高度比风障高度低,则下游地形对风速折减系数的影响不明显,如图 8。
台址的斜坡地形增加了流场的复杂程度,斜坡南高北低,增强了南边边界地形对风速折减系数的影响,同时削弱了北边边界地形对风速折减系数的影响,如图 4和图 8。上游边界地形的海拔越高,对下游区域的挡风能力越强,但下游树立的风障,其减风能力一定程度上有所削弱,且风速折减系数与地形高度非线性相关。因此,在进行风障风场仿真时,尤其是相对复杂的地形工况,上游边界要尽量延伸到相对较高山体的外围,以保障风场仿真的可靠性。表 1中北方向来风,1a地形在天线位置的风速折减系数为40.65 %,2a地形在天线位置的风速折减系数为47.31%,差值大于6%。
分析图 4可知,台址实际斜坡地形,双风障在北方向来风的挡风效率要远弱于南方向来风的挡风效率。因此,风障的实际布置,北边布置的风障高度要高于南边风障的高度。比较图 6和图 10,相同孔隙率的风障,斜坡地形天线位置的回流旋涡明显,而水平地形天线位置没有回流。触发流动分离现象产生的条件,除了地形因素,还与风障的高度、孔隙率等参量有关。在确定的地形工况条件下,可以通过改变风障高度、孔隙率来调节风障下游的流场。
3 结论本文以奇台射电望远镜台址地形为研究对象,利用数值模拟方法研究了不同边界地形对台址风场调控的影响。为了比较台址斜坡地形对风场流动的主导影响以及明确边界地形对风场调控的影响关系,我们构建了台址水平地形对照组。对不同地形仿真结果的分析表明,在无风障工况中,无论台址是斜坡地形还是构建的水平地形,天线位置的风速大小主要与上下游边界地形的最高海拔有关,海拔越高天线位置的风速越小。在有风障工况中,目标区域为水平地形时,风障遮蔽区降低风速的大小主要与上游入流风攻角有关,入流风攻角越大(无风障工况下),风障遮蔽区降低的风速值越大。而风障下游,地形海拔越高,风障遮蔽区降低风速的值也越大。台址的斜坡地形增加了流场的复杂程度,在进行风障风场仿真时,上游边界要尽量延伸到相对较高山体的外围,以保障风场仿真的可靠性。当风障布设的位置确定时,可以通过改变风障高度、孔隙率等参量来调节风障下游的流场。
| [1] |
程景全. 天文望远镜原理和设计[M]. 南京: 南京大学出版社, 2020. CHENG J Q. Principles of astronomical telesecope design[M]. Nanjing: Nanjing University Press, 2020. |
| [2] |
魏善祥, 王启明, 孔德庆, 等. 大型双反射面天线指向误差评估算法[J]. 天文研究与技术, 2020, 17(4): 513–521 WEI S X, WANG Q M, KONG D Q, et al. Algorithm for estimating pointing error of large dual-reflector antenna[J]. Astronomical Research & Technology, 2020, 17(4): 513–521. DOI: 10.14005/j.cnki.issn1672-7673.2020.04.002 |
| [3] |
姚蕊, 李庆伟, 孙京海, 等. FAST望远镜馈源舱精度分析研究[J]. 机械工程学报, 2017, 53(17): 36–42 YAO R, LI Q W, SUN J H, et al. Accuracy analysis on focus cabin of FAST[J]. Journal of Mechanical Engineering, 2017, 53(17): 36–42. |
| [4] |
王新华, 陈东, 罗林, 等. 基于ARM架构的嵌入式系统在自动气象监测系统的应用: 以NVST气象站为例[J]. 天文研究与技术, 2021, 18(1): 108–114 WANG X H, CHEN D, LUO L, et al. The application of ARM-based embedded system in automatic weather monitoring system: NVST weather station as an example[J]. Astronomical Research & Technology, 2021, 18(1): 108–114. |
| [5] | HE F L, XU Q, WANG N, et al. Research on wind tower position optimization method of radio telescope site based on numerical simulation[J]. Chinese Astronomy and Astrophysics, 2021, 45(1): 118–130. DOI: 10.1016/j.chinastron.2021.02.008 |
| [6] |
王从思, 王雪晴, 许谦, 等. 基于等效风场试验的QTT台址风场分布调控技术方案初探[J]. 中国科学: 物理学力学天文学, 2019, 49(9): 130–136 WANG C S, WANG X Q, XU Q, et al. Preliminary study of regulation technology of wind field distribution on QTT site based on test of equivalent wind field[J]. Scientia Sinica: Physica Mechanica & Astronomica, 2019, 49(9): 130–136. |
| [7] | BASNET K, CONSTANTINESCU G, MUSTE M, et al. Method to assess efficiency and improve design of snow fences[J]. Journal of Engineering Mechanics, 2015, 141(3): 04014136. DOI: 10.1061/(ASCE)EM.1943-7889.0000871 |
| [8] | BENDJEBBAS H, EL-HADJ A A, ABBAS M. Numerical simulation of the effect of wind barrier openings on high-speed wind flow around a heliostat field[J]. Applied Mathematical Modelling, 2018, 61: 443–456. DOI: 10.1016/j.apm.2018.04.009 |
| [9] |
许栋, 张博曦, 及春宁, 等. 防风网扬尘庇护区湍流流场模拟数值边界条件[J]. 环境工程学报, 2018, 12(10): 2825–2832 XU D, ZHANG B X, JI C N, et al. Numerical boundary conditions for simulation of turbulent flow field in the shielding zone behind windbreaks[J]. Chinese Journal of Environmental Engineering, 2018, 12(10): 2825–2832. DOI: 10.12030/j.cjee.201806060 |
| [10] |
王争鸣. 兰新高铁穿越大风区线路选线及防风措施设计[J]. 铁道工程学报, 2015, 32(1): 1–6 WANG Z M. Design of route selection and windproof measures for strong wind-hit section of second double line of Lanzhou-Urumqi railway[J]. Journal of Railway Engineering Society, 2015, 32(1): 1–6. DOI: 10.3969/j.issn.1006-2106.2015.01.001 |
| [11] | FANG H, WU X X, ZOU X, et al. An integrated simulation-assessment study for optimizing wind barrier design[J]. Agricultural and Forest Meteorology, 2018, 263: 198–206. DOI: 10.1016/j.agrformet.2018.08.018 |
| [12] | LEE S J, KIM H B. Laboratory measurements of velocity and turbulence field behind porous fences[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 80(3): 311–326. DOI: 10.1016/S0167-6105(98)00193-7 |
| [13] |
许恩乐, 周驰, 李韶璞, 等. 平面型防风网阻力系数的研究[J]. 化学工程, 2017, 45(7): 49–55 XU E L, ZHOU C, LI S P, et al. Research on drag coefficient of planar porous fence[J]. Chemical Engineering, 2017, 45(7): 49–55. |
| [14] | SAN B, WANG Y, QIU Y. Numerical simulation and optimization study of the wind flow through a porous fence[J]. Environmental Fluid Mechanics, 2018, 18(5): 1057–1075. DOI: 10.1007/s10652-018-9580-1 |
| [15] | LOCKMAN F J. The Green Bank Telescope: an overview[C] // Proceedings of SPIE. 1998, 3357: 656-665. |
| [16] | BACH U, KRAUS A. Effelsberg Radio Observatory 2019-2020 report[R]. Bonn: Max-Planck-Institut für Radioastronomie, 2020. |
| [17] |
王娜. 新疆奇台110米射电望远镜[J]. 中国科学: 物理学力学天文学, 2014, 44(8): 783–794 WANG N. Xinjiang Qitai 110 m radio telescope[J]. Scientia Sinica: Physica Mechanica & Astronomica, 2014, 44(8): 783–794. |
| [18] |
闫姝, 曾崇济, 王晓东, 等. 多山地形风场流动数值模拟[J]. 热力发电, 2020, 49(6): 77–83 YAN S, ZENG C J, WANG X D, et al. Numerical simulation of wind farm flow on multi-hill terrain[J]. Thermal Power Generation, 2020, 49(6): 77–83. |
| [19] |
杨立国, 严亚林, 李宏海. 某滑雪场复杂山地地形风场的风洞试验与数值模拟研究[J]. 建筑结构, 2020, 50(11): 135–140 YANG L G, YAN Y L, LI H H. Wind tunnel test and numerical simulation of complex mountainous terrain wind field in a ski resort[J]. Building Structure, 2020, 50(11): 135–140. |
| [20] |
段静, 潘建荣, 徐昕. 基于山地环境的尾流分布特征的风洞试验[J]. 科学技术与工程, 2021, 21(8): 3231–3236 DUAN J, PAN J R, XU X. Wind tunnel test based on wake distribution characteristics of mountainous environment[J]. Science Technology and Engineering, 2021, 21(8): 3231–3236. |
| [21] |
徐洪涛, 何勇, 廖海黎, 等. 防风网气动特性参数的试验研究[J]. 安全与环境学报, 2010, 10(1): 70–74 XU H T, HE Y, LIAO H L, et al. Experimental study on the aerodynamic characteristic parameter of windbreak[J]. Journal of Safety and Environment, 2010, 10(1): 70–74. |
| [22] | GUO L, MAGHIRANG R G. Numerical simulation of airflow and particle collection by vegetative barriers[J]. Engineering Applications of Computational Fluid Mechanics, 2012, 6(1): 110–122. |
| [23] | HE F L, XU Q, WANG N, et al. A method to obtain the wind field characteristics of super-large aperture radio telescope site based on single-point wind tower and numerical simulation[J]. Research in Astronomy and Astrophysics, 2020, 20(12): 82–90. |
| [24] | 朱德庆. 防风网减风效果的雷诺数效应研究[D]. 大连: 大连理工大学, 2020. ZHU D Q. Study on Reynolds number effect of windproof net wind reduction[D]. Dalian: Dalian University of Technology, 2020. |



