2. 中国科学院高能物理研究所, 北京 100049
2. Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China
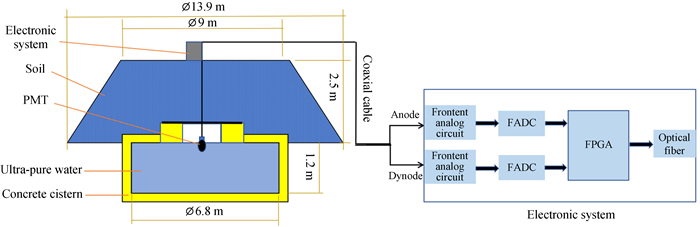
高海拔宇宙线观测站通过探测器探测初级宇宙线粒子经过广延大气簇射(Extensive Air Shower, EAS)后产生的次级粒子,通过重建、分析给出原初宇宙线的相关信息。地面簇射阵列(KM2A)作为高海拔宇宙线观测站的主体阵列,由电磁粒子探测器(Electron Detector, ED)阵列和缪子探测器阵列组成,用来探测广延大气簇射中的次级电磁粒子和缪子,从而开展超高能宇宙线起源和宇宙线物理的研究。其中,缪子探测器的布置总面积达40 000 m2,共计1 188个探测单元,采用反射式水切伦科夫探测技术对广延大气簇射中的缪子成分进行探测。缪子探测器的大面积铺设极大提高了对原初伽马射线的鉴别能力,实现了对超高能伽马射线的高灵敏度探测,直接瞄准解决超高能宇宙线起源这一目标。广延大气簇射次级缪子含量测量有助于我们进行原初宇宙线成分区分和高能强相互作用模型的鉴别,使得LHAASO可以精确测量“膝”区成分能谱,进而破解“膝”区成因这一难题[1-3]。缪子探测器单体设计如图 1,罐体上面覆盖2.5 m厚的土层,吸收缪子探测器中的电磁成份,提高探测器探测到缪子的纯度。在圆柱形水泥罐中放置一个密封性能良好且有高反射率内层的水袋,水袋中灌入超纯水。缪子穿过水袋时在水体中产生切伦科夫光,这些光子在水中传播时被内袋反射,最终有一部分光子由安装在袋子上表面中央的光电倍增管(Photo Multiplier Tube, PMT)接收[4-5]。光电倍增管输出阳极和打拿极信号,通过同轴电缆接入电子学,经过前端模拟电路整形后送入flash ADC进行采样,采样数据送入现场可编程门阵列(Field Programmable Gate Array, FPGA)中进行实时处理,最终通过光纤输出[6]。
|
| 图 1 缪子单元探测器结构示意图(LHAASO MD) Fig. 1 Schematic diagram of MD unit detector (LHAASO MD) |
缪子探测器要求达到的动态范围是1~10 000个粒子,为实现大动态范围测量,采用阳极和第七打拿极共同读出的方式,阳极为1~166个粒子,打拿极为58~10 000个粒子[4]。由于采用阳极加打拿极共同读出的方式,需要建立较为准确的阳极和打拿极连接关系。同时,阳极信号饱和后将强制转换为打拿极信号,此时打拿极信号较小,存在电子学非线性较大、测量误差较大的问题。为了减小测量误差,本文提出了一个缪子探测器电荷测量优化方案,并利用数值模拟和全波形数据分析其可行性,验证其有效性。
1 缪子探测器电荷测量优化方法 1.1 电子学输入信号特征目前观测到的宇宙线能量跨10多个数量级,流量强度跨30个数量级,它的能谱总体上服从简单的幂率分布,高能宇宙线经过广延大气簇射形成的缪子流量强度也基本呈幂率分布[7]。
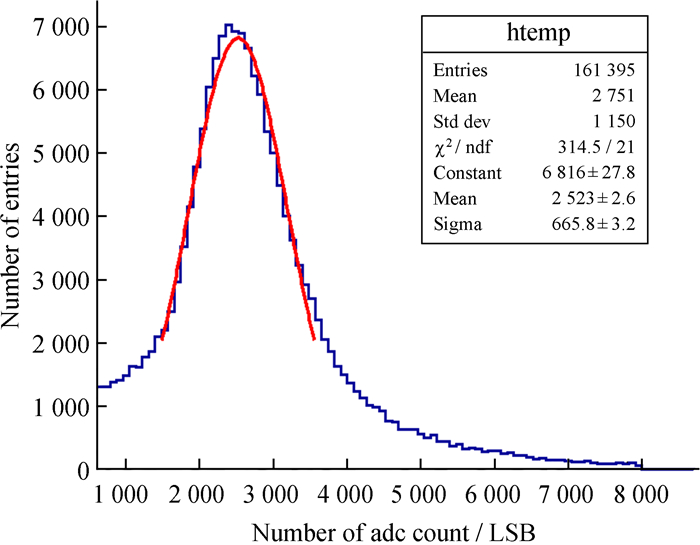
入射缪子探测器的信号经过光电倍增管接收转换为电信号,再输入电子学系统进行处理。探测器的能量分辨率反映了线性探测器区分被探测粒子能量的能力。图 2为单个缪子的积分电荷分布情况,其中平均值(Mean)用于建立缪子与电荷量之间的联系,而单缪能量分辨率Fsingle表示为Fsingle=Sigma/Mean,对于多缪子情况下的能量分辨率,有经验公式FN=Fsingle/N1/2,其中N为入射缪子数。
|
| 图 2 单缪电荷谱 Fig. 2 The charge spectrum of a single muon |
由于缪子探测器采用反射式水切伦科夫探测技术,高能缪子入射缪子探测器后产生的切伦科夫光子经过一次或多次反射后,才能到达光电倍增管,在这个过程中更多的能量被内袋材料和水吸收而损耗,因此会随时间呈指数衰减,单缪波形后沿的衰减时间τ可以用
| $ \frac{1}{\tau}=\left(\frac{1}{\lambda}-\frac{\ln f}{L}\right) \frac{c}{n} $ | (1) |
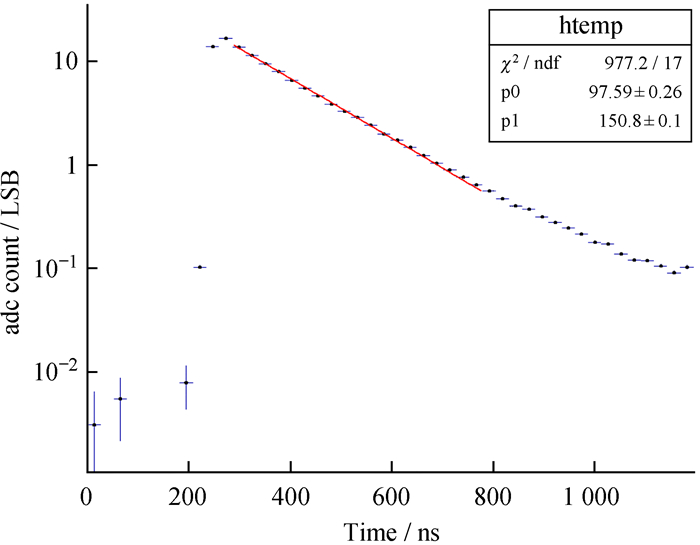
表示,其中,λ为水吸收长度;f为内袋反射率;L为光子在两次与内袋碰撞的平均径迹长度;c为光在真空中的速度;n为光在水中的反射率。在实际情况中,这些参数基本稳定,因此衰减时间也基本稳定。波形前沿上升时间较短(4~9 ns),且随缪子数变化不大[4]。图 3为采用4 000个单缪波形平均化的波形图,前沿上升较快,而后沿为e指数衰减曲线。
|
| 图 3 单缪平均波形 Fig. 3 Mean wave form of a single muon |
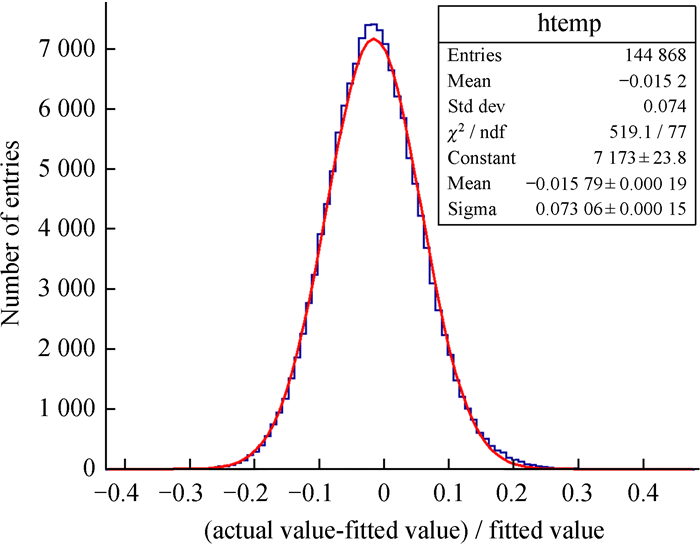
对于平均波形,其后沿为较好的e指数衰减曲线,但对于单个波形来说,光子经过反射后一波一波到达光电倍增管并被吸收,因此,后沿表现为在平均波形附近晃动,即波形特征晃动,晃动幅度与平均波形的幅度相关。对2 000个波形的平均波形进行拟合得到平均值,图 4为单个波形晃动幅度与平均幅度之比的分布情况,基本服从高斯分布。
|
| 图 4 波形特征晃动分布情况 Fig. 4 Characteristic sloshing distribution of waveform |
缪子探测器读出电子学作为前端电子学,主要用于接收缪子探测器的光电倍增管输出信号,完成电荷量Q、时间量T的测量,采样频率为500 MHz。同时,每1 s给出一个信号完整的波形供物理分析使用[8-9]。
电子学的阳极和打拿极信号采用两路独立模数转换器分别进行波形数字化,数字化的信号采用数值积分方法测量电荷量,积分窗口约600 ns,过阈前约100 ns,过阈后约500 ns。模数转换器按时钟节拍对成形后的信号不间断地进行瞬间取样和数字化,得到一系列数字化取样值D0, D1, D2, ..., DN,当触发判选有效时,再对这些数字化的结果进行积分,积分面积与信号电荷量成正比,得到积分面积即可计算电荷量[10]。图 5为电荷积分示意图。
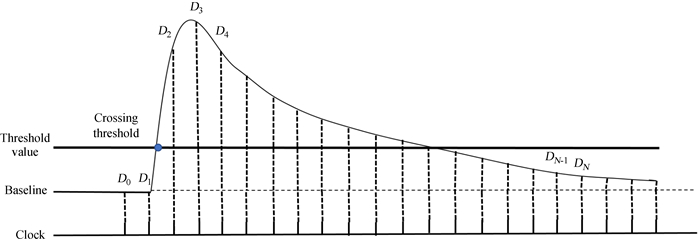
|
| 图 5 电荷积分示意图 Fig. 5 Charge integration diagram |
由于受模数转换器的固有噪声、工艺上的缺陷和各种干扰噪声的影响,电子学本身存在噪声。而电子学台阶的性能反映了电子学噪声水平[10],表现为电子学无信号输入时,输出信号存在晃动现象,如图 6为扣除电子学台阶后的晃动情况。
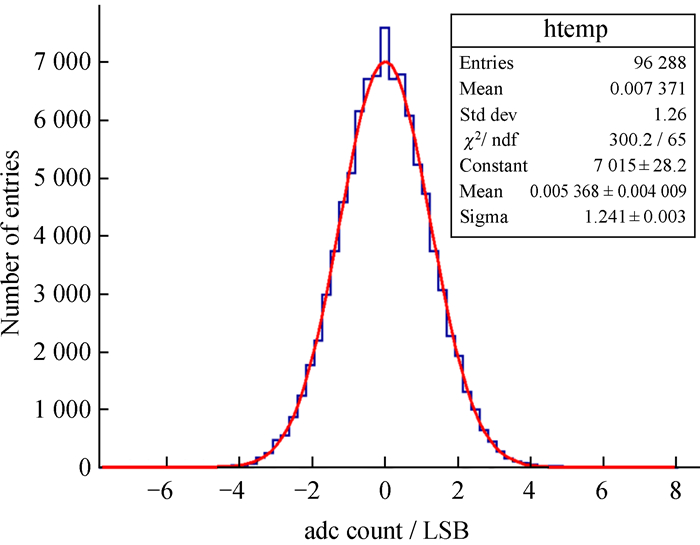
|
| 图 6 电子学台阶晃动分布情况 Fig. 6 Step sloshing distribution in electronics |
对于电子学最终输出的电荷量,阳极信号可以根据单缪电荷标定建立电荷量与缪子数的转换关系,但对于打拿极信号,则需要先将打拿极信号转换为等效阳极信号后才能进一步转换为缪子数,因此,我们需要建立阳极与打拿极之间的转换关系,即AD ratio。AD ratio分为真实值与标定值,其中,真实值为实验室对光电倍增管进行标定得出,标定时采用的测量电子学非线性及误差基本可以忽略,因此真实值反映光电倍增管实际的AD ratio;标定值则是采用光电倍增管配套的读出电子学系统读出数据进行标定,具体标定方法有以下两种:(1)积分电荷(Q)标定法。采用缪子探测器输出的积分电荷进行标定,通过对未饱和阳极信号且信号较大的阳极和打拿极电荷量之比进行拟合可以得到电荷AD ratio,如图 7,其中横坐标为阳极缪子数,纵坐标为打拿极缪子数。由于电荷积分范围为608 ns,在满足一定数据量时,扣除电子学台阶后的晃动平均值为0,AD ratio基本只受电子学非线性影响,因此能真实反映阳极饱和后区域的输出阳极信号与打拿极信号之间的关系。(2)波形峰值(peak)标定法。采用缪子探测器输出的全波形信号进行标定,通过对未饱和阳极信号且信号较大的两路信号波形进行寻峰,得到的峰值进行拟合可以得到峰值AD ratio,与电荷AD ratio的拟合方式一致。由于采用单点标定,受电子学台阶晃动影响,波形的各个点受晃动影响偏大或偏小,打拿极寻到的峰并不一定为真实峰值,因此,进行标定后的AD ratio并不能真实反映阳极与打拿极之间的关系。
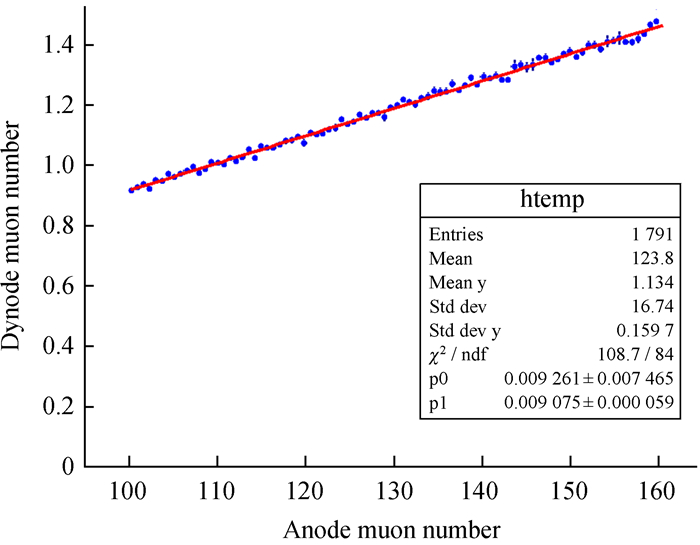
|
| 图 7 电荷AD ratio标定 Fig. 7 AD ratio calibration of charge |
模型的构建主要包括对电子学输入信号和电子学的真实模拟,通过上述分析确定模拟中采用的基本参数如表 1。
| Parameter | Value |
| Exponents of the muon power law spectrum | 2.47 |
| Energy resolution of a single Muse | 25% |
| The attenuation index of the back edge of the waveform | 200 |
| The growth index at the front of the waveform | 4 |
| Waveform characteristic sloshing Guas (mean, sigma) |
Guas (0, 0.10) |
| Charge integration window, ns | 608 |
| DNL Guas (mean, sigma), LSB | Guas (0, 0.30)[11] |
| Electronics step shaking Guas (mean, sigma), LSB |
Guas (0, 1.20) |
采用转换方案测量时,阳极饱和后,在信号较小时AD ratio采用标定值误差较小,信号较大时采用真实值误差较小,两个AD ratio的切换点与标定值之间存在简单的线性关系,通过标定值可以确定AD ratio的切换点。
由于电子学问题,在阳极饱和区域的缪子谱结构出现异常,如图 8(a)为实际数据缪子谱情况,阳极饱和后到AD ratio切换点的区间段(约170~270个缪子)由于AD ratio采用标定值,而标定值实际偏大,计算后的缪子数偏大,出现了图中该区间段谱线下移的现象;300个缪子附近为AD ratio切换点,切换后AD ratio采用真实值,而真实值偏小,计算后的缪子数偏小,出现了图中300个缪子附近曲线向上凸起的现象。模拟得到的缪子谱如图 8(b),模拟与数据缪子谱结构及谱指数十分吻合(< 0.16%),初步验证了模型的可靠性。
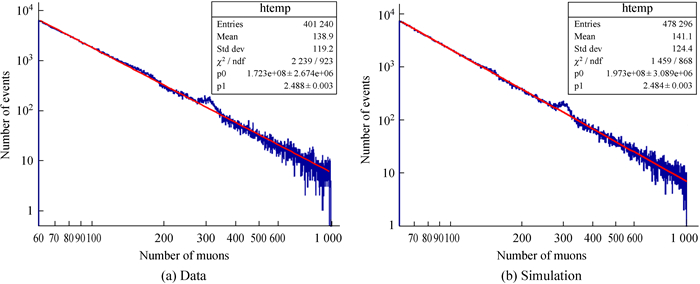
|
| 图 8 转换方案缪子谱结构 Fig. 8 The muon power law spectral structure of the conversion scheme |
对于波形峰值和积分电荷两种AD ratio标定法,我们通过模拟和数据分析了标定值与标定区域缪子数之间的变化关系。
(1) 图 9(a)为AD ratio采用波形峰值标定法进行标定时,AD ratio(按真实值进行归一化)随缪子数的变化情况。缪子数较小时,打拿极峰值受电子学台阶晃动的影响相对较大,寻峰后的打拿极总体峰值偏大,拟合的AD ratio偏小。随着缪子数增大,受电子学台阶晃动的影响相对减小,AD ratio逐渐增大。尽管在大信号时采用峰值标定的AD ratio接近真实值,但仅仅是电子学台阶晃动造成的巧合,当晃动幅度改变时,标定值也发生改变,因此并不能真实反映阳极和打拿极的关系。
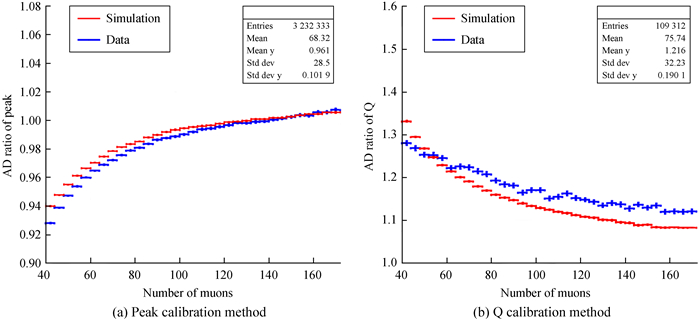
|
| 图 9 AD ratio标定模拟及数据 Fig. 9 AD ratio calibration simulation and data |
(2) 图 9(b)为AD ratio采用积分电荷标定法进行标定时,AD ratio随缪子数的变化情况。缪子数较小时,打拿极受非线性影响较大,积分电荷总体偏小,因此拟合后AD ratio偏大。随着缪子数增大,非线性逐渐减小,AD ratio也逐渐减小。由于电子学最终输出值为电荷量,此时利用电荷量进行标定的AD ratio正好可以真实反映该入射缪子数附近阳极与打拿极之间的关系。模拟与数据之间存在一定偏差,这是由于打拿极信号波形中包含大量小幅度信号,由电子学微分非线性(Differential nonlinearity, DNL)可以得出,此时非线性变化很大,因此相应的AD ratio随缪子数的变化趋势也存在差异。如果要准确测量电荷,应该尽可能避免采用这部分小幅度的信号,这也是采用拼接方案进行电荷测量的一个原因。
2.3 电荷测量拼接方案及模拟现有的电荷测量方案,即转换方案,电子学最终输出为阳极和打拿极积分电荷,在阳极信号饱和后,只能采用打拿极积分电荷进行计算,在阳极饱和区域,打拿极信号较小,受电子学非线性影响,打拿极积分电荷误差较大。因此,通过分析提出采用阳极未饱和部分的信号和阳极饱和部分对应的打拿极信号,两部分信号拼接进行测量,即拼接方案。如图 10,饱和点以下的部分采用阳极信号计算电荷量,而饱和点以上的部分只有打拿极可以测得,这部分采用打拿极信号计算电荷量。由于采用两部分信号测量,阳极部分的信号非线性影响很小,打拿极部分的信号采用波形信号较大的部分,非线性影响也较小,可以有效降低总体测量误差。
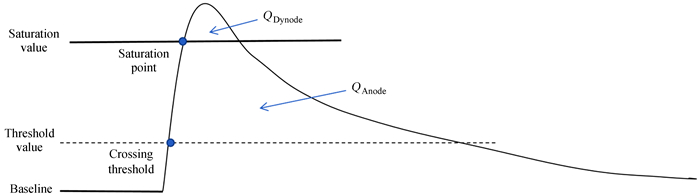
|
| 图 10 拼接方案示意图 Fig. 10 Splicing scheme Diagram |
图 11为采用拼接方案进行模拟的缪子谱,阳极饱和区域的谱结构得到明显改善。由于拼接方案采用未饱和阳极信号和饱和阳极信号对应的打拿极信号,该部分信号非线性较小(< 3%),因此可以直接采用真实值进行计算。图 12为两种方案的电荷积分测量误差模拟,转换方案的AD ratio在缪子数较小时采用标定值,由2.2节图 9(b)可以得出,随着缪子数增加,应该采用的AD ratio逐渐降低至真实值,因此使用标定值计算的积分电荷误差逐渐增大;AD ratio在缪子数较大时采用真实值,此时计算后的积分电荷实际偏小,但随着缪子数的增大误差逐渐降低。拼接方案则只采用真实值计算,此时积分电荷总体偏小,随着缪子数增大,打拿极部分的比例不断上升,误差逐渐增大,但非线性的不断降低使得误差到达最大后又逐渐降低。总之,拼接方案在阳极饱和区域的误差得到有效控制,误差小于1%。
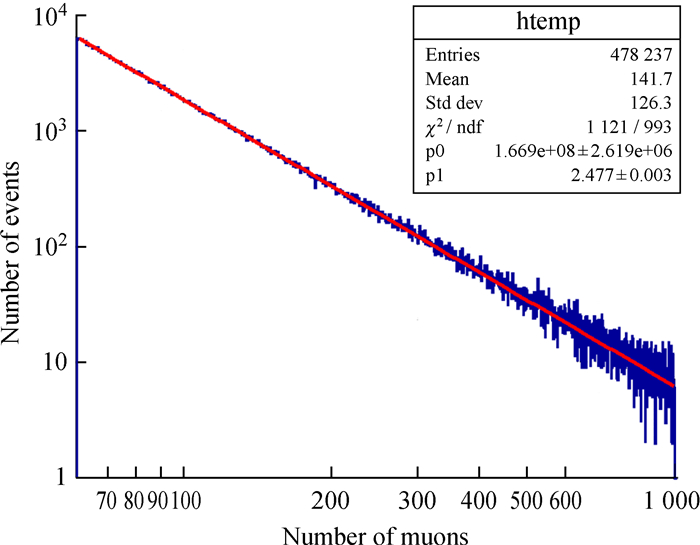
|
| 图 11 拼接方案缪子谱结构(模拟) Fig. 11 The muon power law spectral structure of the splicing scheme (simulation) |
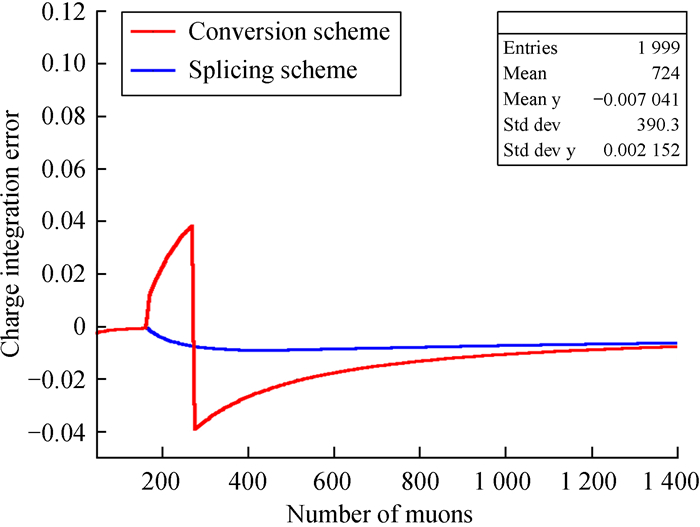
|
| 图 12 转换与拼接方案误差随缪子数变化图 Fig. 12 Conversion and splicing scheme error variation with the number of muon |
缪子探测器每秒输出一次信号完整波形,包括阳极信号和打拿极信号,波形窗口为5 μs,触发前约500 ns,触发后约4 500 ns,利用这些信号可以完成不同目标的物理分析,图 13(a)为单次事例的阳极波形图,图形上方平整部分为阳极饱和区域,对应的打拿极波形如图 13(b)。采用拼接方案进行电荷量计算,电荷积分窗口608 ns,过阈前100 ns,过阈后508 ns。AD ratio使用真实值,得到的缪子谱如图 14,谱结构得到明显改善,同时,谱指数与数值模拟情况十分吻合(< 0.24%),验证了该方案的可行性。
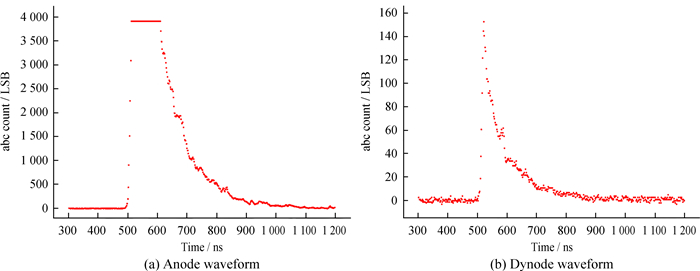
|
| 图 13 阳极饱和时的单个事例波形图 Fig. 13 Single case waveforms at anode saturation |
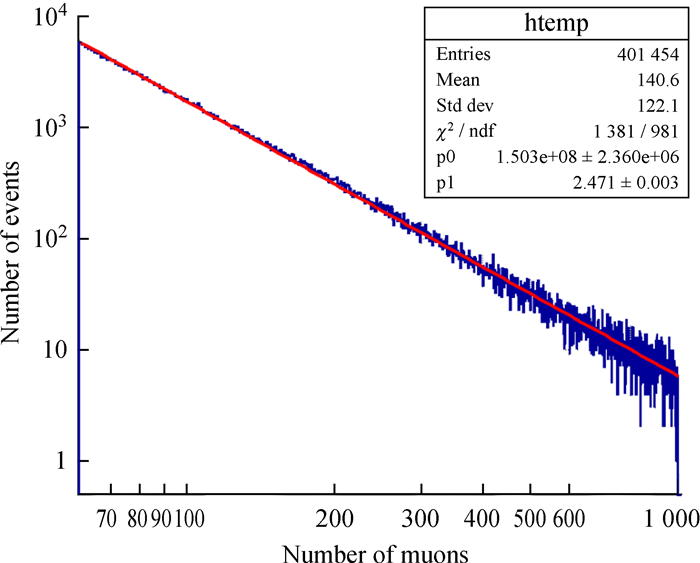
|
| 图 14 拼接方案缪子谱结构(数据) Fig. 14 The muon power law spectral structure of the splicing scheme (data) |
电荷测量方案的模拟及数据分析如表 2,两种方案数据与模拟的谱指数十分吻合,拼接方案与原初模拟谱更接近(< 0.29%)。数据结果中的χ2比模拟情况更大,这是由于使用了1 000个探测器近1年的数据进行分析,不同探测器间存在一定差异,同一探测器不同环境条件下也存在一定差异,但在误差范围内,模拟与数据结果十分吻合。采用拼接方案时可直接使用真实值作为AD ratio,其电荷测量误差 < 1%,此时标定值只作为判断探测器是否存在异常的一个指标。
| Measurement scheme | Spectral index | χ2 | AD ratio | Error/% |
| Conversion scheme (simulation) | 2.484 | 1.681 | True value+calibration value | < 4 |
| Conversion scheme (data) | 2.488 | 2.426 | ||
| Splicing scheme (simulation) | 2.477 | 1.129 | True value | < 1 |
| Splicing scheme (data) | 2.471 | 1.408 |
缪子探测器对广延大气簇射中缪子的精确测量,是实现原初伽马射线鉴别和超高能伽马射线高灵敏度探测的基础。针对阳极、打拿极连接问题,本文通过理论分析和数值模拟相结合的方式,得出拼接方案可以直接采用实验室标定的AD ratio真实值进行连接,探测器反馈数据标定的AD ratio标定值只作为判断探测器是否存在异常的一个指标,有效避免了AD ratio标定及切换可能引入的误差,简化了电荷积分的计算过程。通过数值模拟,我们分析验证了拼接方案可以有效降低阳极饱和区域电荷测量误差,与现在采用的转换方案相比,误差由最大4%降低至最大1%,实现了在1~10 000缪子的大动态范围的精确测量。同时对缪子探测器反馈的全波形信号采用拼接方案计算电荷量,缪子谱结构和谱指数与模拟情况十分吻合,验证了该方案的有效性。
| [1] | CAO Z, DELLA VOLPE D, LIU S M, et al. The Large High Altitude Air Shower Observatory (LHAASO) science book (2021 edition)[J]. Chinese Physics C, 2022, 46(3): 035001. |
| [2] | CAO Z. A future project at tibet: the Large High Altitude Air Shower Observatory (LHAASO)[J]. Chinese Physics C, 2010, 34(2): 249–252. DOI: 10.1088/1674-1137/34/2/018 |
| [3] | 赵晓坤. LHAASO实验中大动态范围光电倍增管性能研究[D]. 合肥: 中国科学技术大学, 2017. ZHAO X K. Study on performance of large dynamic range photomultiplier tube for LHAASO[D]. Hefei: University of Science and Technology of China, 2017. |
| [4] | ZUO X, XIAO G, FENG S H, et al. Design and performances of prototype muon detectors of LHAASO-KM2A[J]. Nuclear Instruments & Methods in Physics Research, 2015, 789(21): 143–149. |
| [5] |
吴文雄, 左雄, 肖刚, 等. LHAASO-MD光电倍增管的性能测试[J]. 天文研究与技术, 2020, 17(2): 258–264 WU W X, ZUO X, XIAO G, et al. The performance test of LHAASO-MD photomultiplier[J]. Astronomical Research & Technology, 2020, 17(2): 258–264. |
| [6] |
王炜, 常劲帆, 刘湘, 等. LHAASO缪子探测器阵列读出电子学系统研制[J]. 核电子学与探测技术, 2015, 35(5): 452–456 WANG W, CHANG J F, LIU X, et al. The design of electronics readout system for LHAASO KM2A muon detector[J]. Nuclear Electronics & Detection Technology, 2015, 35(5): 452–456. |
| [7] | 左雄. LHAASO-KM2A缪子探测器设计与性能研究[D]. 北京: 中国科学院大学, 2015. ZUO X. Design and performances of LHAASO-KM2A muon detector[D]. Beijing: University of Chinese Academy of Sciences, 2015. |
| [8] | 郝新军. LHAASO水切伦科夫探测器原型阵列读出电子学研究[D]. 合肥: 中国科学技术大学, 2011. HAO X J. The research on the readout electronics for the prototype array of LHAASO WCDA[D]. Hefei: University of Science and Technology of China, 2011. |
| [9] |
常劲帆, 王铮, 李秋菊, 等. LHAASO地面粒子探测器阵列前端电子学初步设计[J]. 核电子学与探测技术, 2011, 31(3): 274–276 CHANG J F, WANG Z, LI Q J, et al. Preliminary design of front electronics readout system for LHAASO KM2A[J]. Nuclear Electronics & Detection Technology, 2011, 31(3): 274–276. |
| [10] | 王炜. LHAASO缪子探测器阵列读出电子学系统研制[D]. 北京: 中国科学院大学, 2015. WANG W. The design of electronics readout system for the LHAASO muon detector array[D]. Beijing: University of Chinese Academy of Sciences, 2015. |
| [11] | 何帅. 基于高速采样ADC的多通道数据采集系统[D]. 长沙: 湖南大学, 2012. HE S. Multi-channel data acquisition system based on high speed sampling ADC[D]. Changsha: Hunan University, 2012. |



