2. 中国科学院紫金山天文台, 江苏 南京 210023;
3. 琼台师范学院信息科学技术学院, 海南 海口 571127;
4. 楚雄师范学院数学与计算机科学学院, 云南 楚雄 675099
2. Purple Mountain Observatory, Chinese Academy of Sciences, Nanjing 210023, China;
3. School of Information Science and Technology, Qiongtai Normal University, Haikou 571127, China;
4. School of Mathematics and Computer Science, Chuxiong Normal University, Chuxiong 675099, China
空间目标探测与识别是利用多种手段获取反应目标本质的各种特征和信息,实现对空间目标类型、属性、用途、威胁的判别。空间目标跟踪是获取目标轨道信息的关键手段,跟踪的鲁棒性直接关系到空间目标的自动识别、定位和编目及望远镜的运行效率[1-2]。
目前,国内外主要使用具有普适性的卡尔曼滤波和粒子滤波进行空间目标跟踪,未涉及强干扰和瞬间遮挡目标跟踪方法。非空间运动目标的强干扰和瞬间遮挡处理方法有很多,文[3-7]提出一些非空间目标强干扰和瞬间遮挡处理方法,但没有涉及空间目标强干扰和瞬间遮挡应用的实例,因此需要找到一种恰当的方法处理此问题。空间目标与恒星的强干扰和瞬间遮挡现象经常存在,现广泛应用于天文观测的经典卡尔曼滤波在跟踪强干扰和瞬间遮挡目标时得到的观测数据误差过大,甚至无法获得观测数据。原因在于目标与恒星比较近或者粘在一起,而原有跟踪波门为固定波门,获得的目标质心偏离目标实际质心。
空间目标强干扰和瞬间遮挡主要分为3类:(1)强干扰目标,目标与恒星之间的距离靠近但没有粘在一起,由于靠得很近影响目标正常跟踪;(2)部分遮挡目标,空间目标与恒星瞬间部分遮挡后粘在一起,将目标与恒星当做一颗更大的目标跟踪;(3)完全遮挡目标,即空间目标被恒星完全遮挡,导致找不到跟踪目标,不能有效跟踪。如图 1,图(a)中间位置目标与恒星靠得很近但没有粘在一起,形成干扰现象,图(b)中心位置的目标被恒星部分遮挡,图(c)中间位置有两颗恒星,偏右上的目标被恒星完全遮挡。

|
| 图 1 强干扰和瞬间遮挡目标跟踪的关键问题 Fig. 1 Key problems of strong interference and instantaneous occlusion target tracking |
本文针对上述3个问题提出解决方法,基于卡尔曼滤波能准确预测目标位置,用卡尔曼滤波预判强干扰和瞬间遮挡目标的主要实现过程如下:首先寻找跟踪目标周围的连近恒星,对跟踪目标和连近恒星进行目标与恒星的位置预判。其次进行目标与恒星预判位置之间的距离计算。当距离小于给定阈值时启用新的强干扰和瞬间遮挡目标跟踪方法,即用卡尔曼滤波预测强干扰和遮挡目标的位置并在该预测位置跟踪目标,此时波门沿用前一帧波门的大小,同时用目标的预测质心对波门质心进行限定修正,实现目标稳健跟踪和精确跟踪;当预判距离大于给定的阈值时为普通目标,用卡尔曼滤波与改进的波门结合跟踪目标。实现过程如图 2。
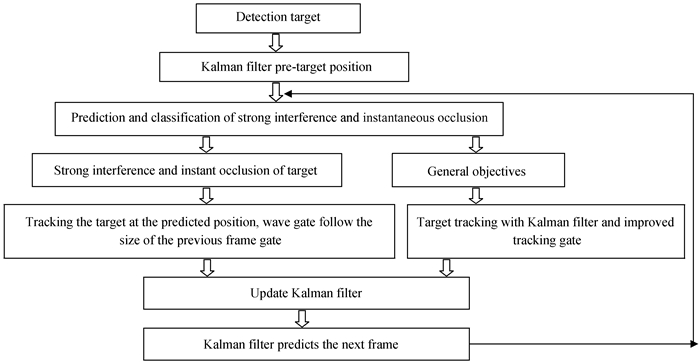
|
| 图 2 新的目标跟踪流程图 Fig. 2 New target tracking flow chart |
令状态向量Xk=[xk, yk, vxk, vyk]T各个值分别代表空间目标x和y方向的位置和速度,观测向量Zk=[xk, yk]T代表空间目标观测位置,由卡尔曼跟踪空间目标时获得。其状态方程和输入的观测方程分别为
| $ \boldsymbol{X}_k=\boldsymbol{A}_k \boldsymbol{X}_{k-1}+\boldsymbol{B}_k \boldsymbol{W}_k, $ | (1) |
| $ \boldsymbol{Z}_k=\boldsymbol{H}_k \boldsymbol{X}_k+\boldsymbol{V}_k, $ | (2) |
其中,Xk和Xk-1分别为k和k-1时刻的状态向量,即根据k-1时刻空间目标状态和控制变量推测k时刻状态;Ak为状态转移矩阵,是对目标状态转换的一种猜想模型;Bk为输入矩阵,将输入转换为状态的矩阵;Hk为观测矩阵,是状态方程到观测方程的转换矩阵;Wk和Vk分别为状态噪声和观测噪声矩阵,对应的方差矩阵分别为Q和R。推导公式为
| $ \boldsymbol{X}_K^{-}=\boldsymbol{A}_k \boldsymbol{X}_{k-1}+\boldsymbol{B}_k \boldsymbol{W}_{k-1}, $ | (3) |
| $ \boldsymbol{P}_k^{-}=\boldsymbol{A}_k \boldsymbol{P}_{k-1} \boldsymbol{A}^{\mathrm{T}}+\boldsymbol{Q}, $ | (4) |
| $ \boldsymbol{K}_k=\boldsymbol{P}_k^{-} \boldsymbol{H}_k^{\mathrm{T}}\left(\boldsymbol{H}_k \boldsymbol{P}_k^{-} \boldsymbol{H}_k^{\mathrm{T}}+\boldsymbol{R}\right)^{-1}, $ | (5) |
| $ \boldsymbol{X}_k=\boldsymbol{X}_k^{-}+\boldsymbol{K}_k\left(\boldsymbol{Z}_k-\boldsymbol{H}_k \boldsymbol{X}_k^{-}\right), $ | (6) |
| $ \boldsymbol{P}_k=\left(I-\boldsymbol{K}_k \boldsymbol{H}_k\right) \boldsymbol{P}_k^{-}, $ | (7) |
其中,XK-为状态预测值;Pk-为协方差矩阵;Kk为卡尔曼增益矩阵;Xk为XK-的修正值;Pk为Xk协方差矩阵。(3)式和(4)式的猜测位置不是最佳预测位置,因为没有考虑当前时刻卡尔曼滤波跟踪目标时获得的观测位置,通过(5)式、(6)式和(7)式对当前观测位置更新修正后输出最佳预测位置并对目标进行跟踪[8-10]。
2 改进的跟踪波门设计鉴于空间目标星像圆整度不好,因此矩方法是最广泛应用的计算空间目标质心的方法。经典卡尔曼滤波采用固定波门方法跟踪空间目标,固定波门对目标大小变化不具有自适应性,跟踪空间目标时常有误差,特别是跟踪强干扰和瞬间遮挡目标时误差频出且相对较大。为此本文提出可变波门,波门可以根据目标大小自适应变化。设图中目标像素点位置为(xk, yk),矩形中心(ax, ay)为
| $ a_x =\frac{\max \left(x_k\right)+\min \left(x_k\right)}{2}, $ | (8) |
| $ a_y =\frac{\max \left(y_k\right)+\min \left(y_k\right)}{2} . $ | (9) |
跟踪波门的宽(w)和高(h)为
| $ w =\max \left(x_k\right)-\min \left(x_k\right), $ | (10) |
| $ h =\max \left(y_k\right)-\min \left(y_k\right) . $ | (11) |
卡尔曼滤波通过不断预测、更新和修正实现空间目标跟踪。强干扰目标和瞬间遮挡目标在空间运动目标观测中经常存在,此类目标易使该帧被跟踪目标的理论位置与实际位置之间的误差进一步增大,甚至无法捕获位置信息,失去跟踪价值。与用于空间目标观测的经典卡尔曼滤波跟踪相比,新方法主要将强干扰目标的预测位置当做观测位置进行目标跟踪,同时跟踪波门沿用前一帧波门,用预测目标质心对波门质心进行修正,实现目标稳健跟踪,并提出基于目标与恒星之间质心距离预判的新方法。
3.1 确定跟踪目标周围连近恒星的预测范围为实现强干扰和瞬间遮挡目标稳健跟踪,连近恒星预判非常重要。如果对整帧图进行大范围的目标质心与恒星质心之间的距离预判,计算量和耗时必然增加,程序的运行效率降低;如果只对目标周围小范围的目标质心与恒星质心之间的距离预判,无法准确判断目标与恒星的强干扰和瞬间遮挡问题。通常以跟踪目标质心为圆点,特定半径R的一个圆周内预测到的恒星判定为连近目标的恒星,恒星预判面积S=πR2。
3.2 目标与恒星的位置预判当运动目标与恒星存在强干扰和瞬间遮挡时,由于恒星干扰不能准确计算目标实际质心位置,这时需要卡尔曼滤波进行位置预测,用上一帧被跟踪目标的实际位置预测当前帧的位置,用上一帧被跟踪恒星的实际位置预测当前帧的位置,即用预测位置代替实际位置进行目标和恒星质心之间的距离计算,当有多帧目标遮挡时需要进行多帧预测。
3.3 目标与恒星的预判位置之间的距离计算设当前帧强干扰和瞬间遮挡目标的预测质心为(xic, yic),对应连近恒星的预测质心为(xkc, ykc),则目标与恒星之间的预测距离为
| $ D=\sqrt{\left(x_{i c}-x_{k c}\right)^2+\left(y_{i c}-y_{k c}\right)^2} . $ | (12) |
为更好判断目标与恒星是否存在强干扰和瞬间遮挡,将目标与恒星之间的预测距离设置阈值F,阈值设置为
| $ K=\left\{\begin{array}{l} 1, D<F \\ 0, D \geqslant F \end{array} .\right. $ | (13) |
当目标与恒星质心之间预测距离大于等于给定阈值时,K取值为0,表示不存在强干扰和瞬间遮挡目标,用卡尔曼滤波与改进的波门结合跟踪目标;当目标与恒星质心之间预测距离小于给定阈值时,K取值为1,表示存在强干扰和瞬间遮挡目标,此时用卡尔曼滤波器的预测位置作为观测位置进行目标跟踪,跟踪波门沿用前一帧波门的大小,并用预测目标质心对波门质心进行限定修正。
3.5 波门限定修正在预测到强干扰和瞬间遮挡目标时,此目标的波门沿用前一帧波门,为确保该帧目标跟踪的鲁棒性,鉴于卡尔曼滤波预测的准确性,将波门质心与预测质心之间的差值限定在特定范围Q,由前一帧获得该帧的预测质心(xic, yic)与该帧获得的波门质心(ax, ay)之间的限定关系为
| $ \left|x_{i c}-a_x\right|<Q, $ | (14) |
| $ \left|y_{i c}-a_y\right|<Q . $ | (15) |
当强干扰和瞬间遮挡目标跟踪结束后,跟踪波门又切换为可变波门跟踪,跟踪方式切换到卡尔曼滤波与改进的波门结合的跟踪方式。
4 实验结果以中国科学院紫金山天文台姚安观测站500 mm口径篱笆光学望远镜拍摄的多帧空间运动目标图像为实验素材,基于戴尔笔记本电脑的WINDOWS 10系统,实验使用pycharm2022软件,python3.9的opencv3.4.17.63程序。本实验用卡尔曼滤波与改进的跟踪波门结合跟踪目标,遇到强干扰和遮挡目标时直接用新的强干扰和瞬间遮挡目标跟踪方法。对比实验用空间运动目标观测系统的经典卡尔曼滤波跟踪目标,波门为固定波门,当存在强干扰和瞬间遮挡目标时不做任何处理。每帧图中红色波门中的白色圆点为空间目标,其余为恒星。
4.1 波门对比实验图 3(a)和(b)用经典卡尔曼滤波跟踪目标,跟踪波门为固定波门,(a)目标比波门大,(b)目标比波门小;(c)和(d)用卡尔曼滤波与改进的可变波门结合跟踪目标,波门收敛于目标质心,避免被跟踪目标理论质心和实测质心误差过大的情况发生。

|
| 图 3 波门对比图 Fig. 3 Comparison diagram of gate |
传统卡尔曼滤波跟踪目标与本文方法对比统计见图 4。由图 4可知,本文方法的精度整体提升,平均提升了1.14倍,验证了本文方法的适用性和有效性。
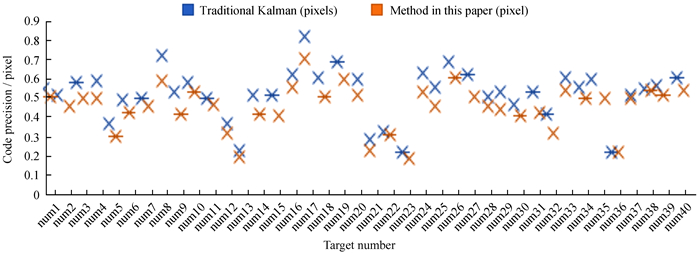
|
| 图 4 目标精度提升 Fig. 4 Accuracy improvement |
图 5(a)和(b)为目标与恒星组成的同一目标强干扰图,但跟踪方式不同。(a)用经典卡尔曼滤波跟踪目标,目标在波门左上角,偏离波门中心,捕获的目标质心误差相对偏大;(b)用强干扰和瞬间遮挡目标处理方法,波门收敛于目标,捕获的目标质心误差相对较小。

|
| 图 5 强干扰目标跟踪对比图 Fig. 5 Comparison diagram of strong jamming target tracking |
图 6将多圈目标分别捕获的强干扰帧进行运动规律分析,如果该帧数据和其他帧保持一样的运动规律,则认为捕获的强干扰帧为有效帧。传统方法与本文方法跟踪强干扰目标对比,本文方法能捕获更多强干扰帧,且捕获的强干扰帧中大部分为有效帧,传统方法捕获较少的强干扰帧且捕获帧中大部分为无效帧。
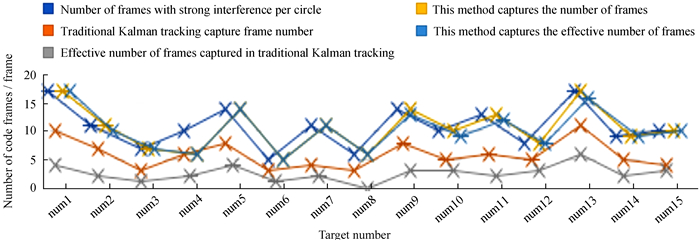
|
| 图 6 强干扰帧中有效帧数增加 Fig. 6 Increase of effective frames in strong interference frames |
图 7为同一目标的两组部分遮挡图,目标由左上向右下运动。(a), (b)和(c)用传统卡尔曼滤波跟踪目标,将目标与恒星当做一颗更大的目标跟踪,导致波门质心位置与目标质心位置之间有一定误差;与(a), (b), (c)对应的(d), (e), (f)用强干扰和瞬间遮挡目标处理方法,在预测位置跟踪目标,根据预测位置沿用前一帧修正波门的大小跟踪目标,得到理想的跟踪结果。

|
| 图 7 部分遮挡目标跟踪对比 Fig. 7 Partial occlusion target tracking comparison |
图 8由同一目标的两组遮挡图组成,其中(a)和(d)完全遮挡。每组红色波门中的目标由右上向左下运动,(a), (b)和(c)用传统卡尔曼滤波进行固定波门跟踪,波门能套住目标,但目标被恒星完全遮挡时将目标与恒星当作一颗更大的目标跟踪,目标质心与波门质心之间有很大误差;(d), (e)和(f)用本文提出的新方法,波门根据预测情况套住目标,同时沿用前一帧波门的大小,并对目标完全遮挡时的波门位置做限定修正,实现稳健跟踪目标,得到有效的观测数据。当望远镜抖动时图 9和图 6一样,根据目标运动规律进行有效帧数统计,即对部分遮挡和完全遮挡帧在传统卡尔曼跟踪目标和本文方法跟踪目标时的有效帧数进行统计,由本文方法捕获部分遮挡和完全遮挡目标的有效帧数大大增加,获得理想的实验效果,进一步突出本文方法的可行性。

|
| 图 8 完全遮挡目标跟踪对比 Fig. 8 Full occlusion target tracking comparison |
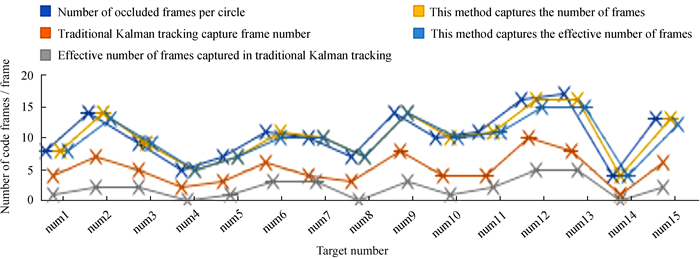
|
| 图 9 遮挡帧中有效帧数 Fig. 9 Effective frame number in occluded frames |
误差影响统计见表 1。由表 1可知,望远镜的跟踪误差越小,跟踪效果越好,随着跟踪误差的增大,望远镜的跟踪有效性变差,误差过大时捕获脱离目标运动轨迹的观测数据,失去意义。
| Error value T/pixel | T ≦ 0.25 | 0.25 ≤ T ≤ 1 | 1 ≤ T ≤ 2 | T ≥ 2 |
| Whether the tracking data is valid | Very good | Valid | Occasionally invalid | Poor effect |
当望远镜抖动时,对抖动帧进行跟踪时捕获的观测数据误差过大,无法获得有效数据,但在无抖动帧跟踪误差比较小且抖动不频繁时,直接用预测值代替抖动帧的观测值,可以获得有效的观测数据。当抖动频繁且过大时,无法获得跟踪数据,也无法用预测值代替观测值进行目标跟踪。
外界环境因素和设备自身因素影响会使信噪比过小、暗噪声过大等情况发生,导致跟踪目标时跟丢或跟错,捕获无效观测数据。当检测到跟踪环境异常且获得无效观测数据时,可用预测值代替观测值获得目标的观测位置。
5 总结空间目标与碎片的观测研究是获取目标轨道数据、掌握空间态势的重要组成部分,是空间科学发展进步必不可少的。强干扰和瞬间遮挡目标的有效跟踪对于获取更多有价值的数据至关重要,它能降低数据错误率,提高数据质量,为获取轨道位置提供更多精确的数据。为此,本文跟踪方法基于传统的卡尔曼滤波算法,将波门改为根据目标大小自适应变化,并设置新的强干扰和瞬间遮挡目标预判和跟踪方法。方法不仅适用于普通目标跟踪,而且对强干扰和瞬间遮挡目标跟踪具有理想的跟踪效果,具有一定的适用性。
| [1] |
王雪瑶. 国外空间目标探测与识别系统发展现状研究[J]. 航天器工程, 2018, 27(3): 86–94 WANG X Y. Development status research of foreign space target detection and identification systems[J]. Spacecraft Engineering, 2018, 27(3): 86–94. |
| [2] |
薛喜平, 张洪波, 孔德庆. 深空探测天文自主导航技术综述[J]. 天文研究与技术, 2017, 14(3): 382–391 XUE X P, ZHANG H B, KONG D Q. An overview of celestial autonomous navigation technology for deep space exploration[J]. Astronomical Research & Technology, 2017, 14(3): 382–391. |
| [3] |
平一鼎. 人造卫星观测中重叠像的分离[J]. 天文学报, 2008, 49(3): 321–326 PING Y D. Separating the blended images in space object observation[J]. Acta Astronomica Sinica, 2008, 49(3): 321–326. |
| [4] | WANG Y, FANG Y W, ZHANG J, et al. Dezert-Smarandache theory for multiple targets tracking in natural environment[J]. IET Computer Vision, 2013, 7(6): 456–466. DOI: 10.1049/iet-cvi.2012.0193 |
| [5] | HU Y H, SHENG X H. Dynamic sensor self-organization for distributive moving target tracking[J]. Journal of Signal Processing Systems, 2008, 51(2): 161–171. DOI: 10.1007/s11265-007-0104-3 |
| [6] |
耿立红, 苏仓, 杜静, 等. 遮挡效应的太阳射电观测和仿真[J]. 天文研究与技术, 2023, 20(1): 15–23 GENG L H, SU C, DU J, et al. Solar radio observing and simulation of shadowing effect[J]. Astronomical Research & Technology, 2023, 20(1): 15–23. |
| [7] |
张根耀, 李竹林, 赵宗涛. 遮挡情况下运动目标的跟踪[J]. 安徽大学学报(自然科学版), 2003(3): 30–34 ZHANG G Y, LI Z L, ZHAO Z T. A Trace method for moving target under occlusion[J]. Journal of Anhui University (Natural Science Edition), 2003(3): 30–34. |
| [8] |
闫晓辉, 张玉衡, 宋谦. 基于定标和图像处理的数字相机串扰图像修正方法[J]. 天文研究与技, 2023, 20(2): 135–144 YAN X H, ZHANG Y H, SONG Q. Method for crosstalk image correction of digital camera based on calibration and image processing[J]. Astronomical Research & Technology, 2023, 20(2): 135–144. |
| [9] |
潘祖恒, 彭青玉, 陆星, 等. 利用图像相关性搜寻运动目标[J]. 天文研究与技术, 2023, 20(1): 41–49 PAN Z H, PENG Q Y, LU X, et al. Searching moving objects by image correlation[J]. Astronomical Research & Technology, 2023, 20(1): 41–49. |
| [10] | YANG Y J, FAN X G, WANG S D, et al. Target tracking based on amendatory Kalman filter[J]. Systems Engineering and Electronics, 2014, 36(5): 846–851. |



