2. 广西相对论天体物理重点实验室, 广西 南宁 530004
2. Guangxi Key Laboratory for Relativistic Astrophysics, Nanning 530004, China
耀变体是带有喷流的射电噪活动星系核(Active Galactic Nuclei, AGN),它们构成了一类特殊的活动星系核。在整个电磁波谱上,耀变体具有非热连续谱,相对论喷流指向地球[1]。根据其光学光谱特征,它们通常分为两个亚类,即平谱射电类星体和蝎虎座BL型天体[1]。平谱射电类星体具有显著的宽发射线,其等值宽度>0.5 nm,而蝎虎座BL型天体的光谱是平滑的连续谱或仅显示弱线。耀变体两个亚类的主要区别在于它们的发射线,也可以根据活动星系核的不同吸积机制进行划分,即平谱射电类星体比蝎虎座BL型天体具有较高的吸积率[2-4]。还有研究者提出用中心黑洞自旋划分平谱射电类星体和蝎虎座BL型天体,即蝎虎座BL型天体的中心黑洞的旋转速度比平谱射电类星体的慢[5]。
1998年,文[6]发现了耀变体序列。耀变体序列表明,在耀变体的宽波段光谱能量分布中有两个明显的成份(能量低的为同步峰,能量高的为逆康普顿峰),随着同步峰值频率向蓝端移动, 辐射热光度减小,即同步峰值光度与峰值频率成反比。平谱射电类星体的同步峰值频率一般小于1014 Hz,而蝎虎座BL型天体的同步峰值频率分布比平谱射电类星体的宽得多。所以,该亚类又进一步分成高峰频(大于1015 Hz)、中峰频(1014 < νpeak < 1015)和低峰频(小于1014 Hz)蝎虎座BL型天体[7]。正是由于耀变体两个亚类的同步峰值频率的分布差异,宽波段谱指数(复合光谱指数)分布中常常出现双峰结构。另外,谱指数-谱指数图中出现明显的成团性,该特征具有一定的分类作用。相比于光谱能量分布图,谱指数更容易在巡天数据库中获得,因此更适合在巡天大样本中快速区分耀变体的两个亚类。
费米大面积望远镜自2008年在轨运行以来发现了大量的伽马射线源,其中耀变体占绝大多数[7-8],也包括大量不确定类型的耀变体。通常,这些耀变体由于没有确凿的光谱观察而不能确定是否是平谱射电类星体或蝎虎座BL型天体。本文对第4期费米大面积望远镜活动星系核目录第三批发布数据(4LAC-DR3),以谱指数-谱指数图为基础,将复合光谱指数作为机器学习程序的输入参数,对该目录中的耀变体进行分析研究。
1 样本费米伽马射线空间望远镜(Fermi)团组于2022年公布了新的伽马射线源目录(4FGL-DR3)[9]。基于12年的伽马射线观测数据,该目录包含6 658个伽马射线源,其中4 501个源找到了其他波段的对应体,剩下2 157个源没有找到对应体。有其他波段对应体的源主要是耀变体,约占91%,这些耀变体中1 457个是蝎虎座BL型天体,794个是平谱射电类星体,剩下1 492个是不确定类型的耀变体候选体[9]。基于这个目录(4FGL-DR3),我们通过法国斯特拉斯堡天文台的数据库(Strasbourg astronomical Data Center, CDS, http://cdsxmatch.u-strasbg.fr/#tab=xmatch&),与多巡天数据库进行交叉匹配,得到多波段数据。我们总共得到了7个波段的数据,这7个波段分别为γ-ray, X-ray, WISE w1, w2和w3波段, 射电波段(1.4 GHz),Gaia卫星的g波段。表 1给出了各个波段的样本数量。
| Band | Sample size | ||
| FSRQ | BL Lac | BCU | |
| γ-ray | 750 | 1 410 | 1 516 |
| Radio | 608 | 886 | 927 |
| Gaia g | 723 | 1 361 | 1 146 |
| Swift X-ray | 314 | 551 | 134 |
| WISE w1 | 726 | 1 356 | 1 237 |
| WISE w2 | 726 | 1 356 | 1 237 |
| WISE w3 | 726 | 1 356 | 1 234 |
耀变体的光谱斜率常用能谱指数描述。其中,两点(复合)光谱指数(Two-point Spectral Indices)可以在一定程度上描述耀变体的宽波段能谱能量分布的形状。两点光谱指数也称为宽波段谱指数或者复合谱指数,其本质是能谱上两点间的斜率。两点(复合)光谱指数可通过
| $ \alpha_{12}=-\frac{\log \left(\frac{F_1}{F_2}\right)}{\log \left(\frac{v_1}{v_2}\right)} $ | (1) |
计算(Ledden & O′Dell 1985)[10],其中,F1和F2分别是频率ν1和ν2时的流量密度。使用(1)式将星等转换为流量密度,
| $ -2.5 \lg (f)=m-F_0 \text {, } $ | (2) |
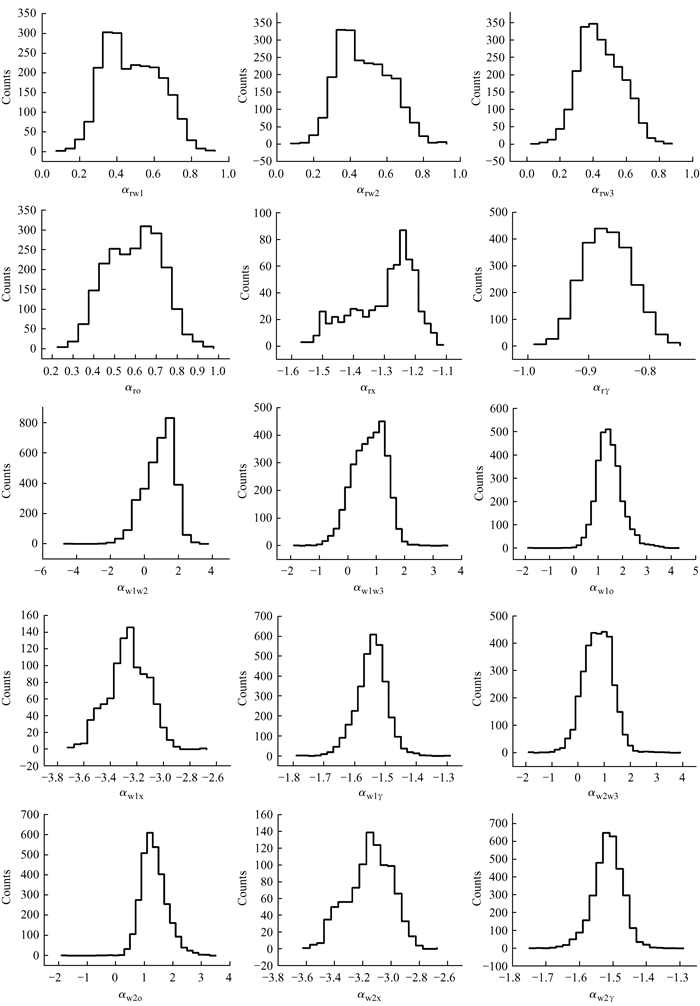
其中,F0为零星等流量;m为星等值;f为对应的流量密度。对于样本中的所有耀变体,我们使用频率为射电波段(1.4 GHz),w1(3.4 μm),w2(4.6 μm),w3(12 μm),g(330~1 050 nm),1 keV和100 MeV处的通量密度计算了射电、红外、光学、X射线、γ射线两两之间的谱指数。图 1~图 2给出了表 1中列出的7个波段排列组合得到的21个光谱指数分布。
|
| 图 1 宽波段谱指数分布图 Fig. 1 Broadband spectral index distribution |
|
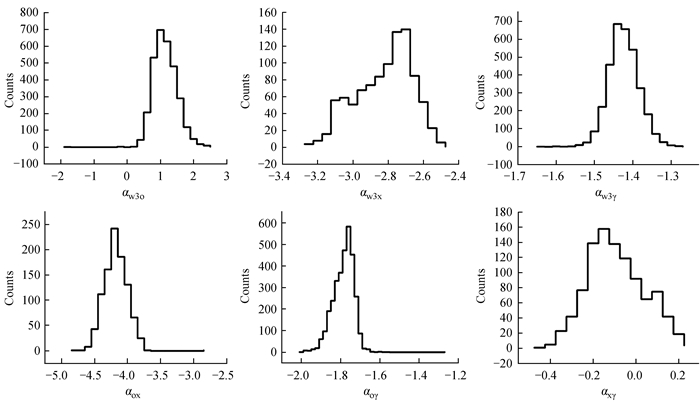
| 图 2 宽波段谱指数分布图 Fig. 2 Broadband spectral index distribution |
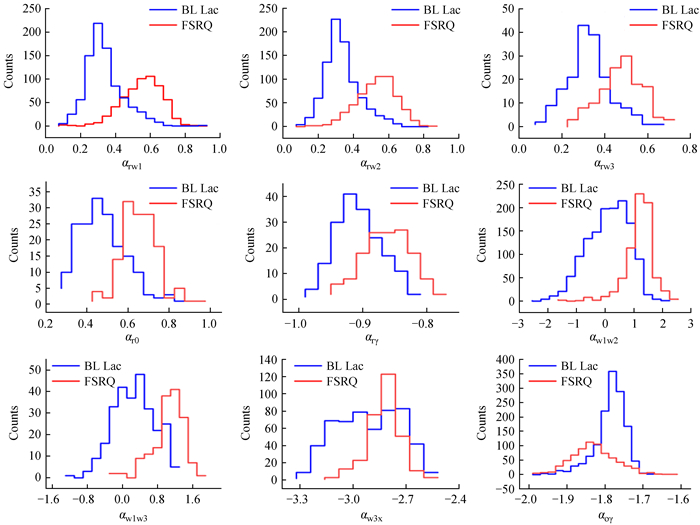
从图 1~图 2可以看出,9个宽波段谱指数αrw1,αrw2,αrw3,αro,αrγ,αw1w2,αw1w3,αw3x和αoγ的分布具有微弱的双峰结构,其他12个宽波段谱指数的分布并没有双峰结构。这种双峰结构可能分别对应于耀变体的两个亚类。这也表明平谱射电类星体与蝎虎座BL型天体之间可能存在不同的能谱特性。为了进一步验证上述9个宽波段谱指数对耀变体两个子类的分布差异,我们将两个子类的分布对比画在一起,如图 3。我们发现除了αoγ之外,其他8个谱指数都能明显区分平谱射电类星体与蝎虎座BL型天体。
|
| 图 3 耀变体的两个亚类(FSRQ与BL Lac)的宽波段谱指数分布图 Fig. 3 The distribution of the broad band spectral index of the two subclasses (FSRQ and BL Lac) of the blazar |
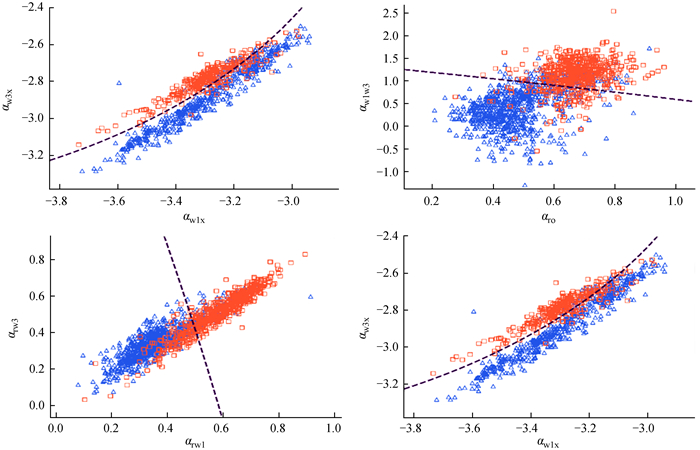
在第2节中,我们看到单个谱指数分布图对耀变体两个子类的区分度并不强,我们需要进一步考虑谱指数-谱指数图。如图 4,我们可以在谱指数-谱指数图上看到耀变体的两个亚类有明显的成团性。
|
| 图 4 4个典型的谱指数-谱指数图。红色方框代表平谱射电类星体,蓝色三角形代表蝎虎座BL型天体 Fig. 4 Four typical spectral index-spectral index planes. The red box represents FSRQ, and the blue triangle represents BL Lac |
为了更好地分析谱指数-谱指数图对耀变体的分类作用,我们需要为机器学习方法选择合适的参数和算法[11-14]。文[15]认为支持向量机的分类算法效果比较好。支持向量机分类算法是在特征空间中寻找一个超平面来区分不同类别的算法,使得该超平面与两个类别的距离最大,进而达到分类的目的。支持向量机是有监督的机器学习方法。一般情况下大部分数据集是线性不可分的,因此需要把数据集从低维的特征空间映射到高维的特征空间,从而达到更好的分类效果。常见的核函数有线性核、多项式核、径向基函数核等。我们也采用支持向量机,并下载了相关的Python程序模块(https://scikit-learn.org/stable/modules/svm.html#svm-classification)。我们把蝎虎座BL型天体称为正类,平谱射电类星体称为负类。根据这个定义,正确分类的蝎虎座BL型天体称为真阳性TP(True Positive),而正确分类的平谱射电类星体为真阴性TN(True Negative);把蝎虎座BL型天体错误地预测为平谱射电类星体称为假阳性FP(False Positive),而把平谱射电类星体错误地预测为蝎虎座BL型天体则称为假阴性(False Negative)。对于二分类,以上符号可以用表 2描述,最上面一行表示真实类标签,最左边一列表示预测类别。
| True BL Lac | True FSRQ | |
| Predicted BL Lac | TN | FN |
| Predicted FSRQ | FP | TP |
根据常用的分类性能指标,准确率(Accuracy Rate, AR)计算公式为[15-16]
| $ A R=\frac{T P+T N}{T P+F P+T N+F N} . $ | (3) |
图 4给出了表 3列出的210个谱指数-谱指数图中成团性较好的4个典型图,图中虚线为模型给的两类耀变体的分界线,具体是通过计算谱指数图中的点属于平谱射电类星体的概率以及属于蝎虎座BL型天体的概率,两者概率之差为0的点即组成该分界线。从图 4可以看出,平谱射电类星体和蝎虎座BL型天体主要占据不同的区域,这表明它们具有不同的能谱特性。但是,我们也可以看到两类耀变体占据区域有一部分重合,其中右下图重合部分较多,分界不清晰,因而更需要机器学习的方法进行分类。图 4显示平谱射电类星体和蝎虎座BL型天体谱指数之间的关系表明它是复杂的,这也与之前的结论一致[17-21]。表 3中第3、6、9和12列给出了谱指数-谱指数图对耀变体两个子类的分类准确率。
| Planes | Sample size | Accuracy rate/% | Planes | Sample size | Accuracy rate/% | Planes | Sample size | Accuracy rate/% | Planes | Sample size | Accuracy rate/% | |||
| αw1x-αw3x | 845 | 88.8 | αrw1-αrx | 582 | 84.7 | αrγ-αw2γ | 1 450 | 83.0 | αw2γ-αw3x | 845 | 74.7 | |||
| αw1w2-αox | 842 | 87.8 | αrw1-αw1w3 | 1 450 | 84.7 | αro-αoγ | 1 451 | 82.8 | αw2o-αoγ | 2 045 | 74.5 | |||
| αw1w2-αw1x | 845 | 87.8 | αrw1-αw3x | 582 | 84.7 | αrw2-αw3x | 582 | 82.8 | αox-αxγ | 859 | 74.3 | |||
| αw1x-αw2x | 845 | 87.8 | αw2w3-αw2x | 845 | 84.7 | αrw2-αrx | 582 | 82.6 | αrx-αxγ | 598 | 74.1 | |||
| αro-αw1x | 579 | 87.7 | αro-αw1γ | 1 422 | 84.5 | αrx-αw2w3 | 582 | 82.5 | αw3γ-αoγ | 2 045 | 74.0 | |||
| αw1w2-αw2x | 845 | 87.7 | αrw1-αxγ | 582 | 84.5 | αw2o-αw3o | 2 045 | 82.3 | αw2x-αoγ | 842 | 73.9 | |||
| αw2x-αw3x | 845 | 87.6 | αrw3-αw3o | 1 422 | 84.5 | αrγ-αw1w3 | 1 450 | 82.2 | αw1γ-αw3x | 845 | 73.8 | |||
| αro-αw2x | 579 | 87.4 | αrx-αw2x | 582 | 84.5 | αw2w3-αw2o | 2 045 | 82.2 | αrγ-αxγ | 598 | 73.7 | |||
| αw1w2-αw3x | 845 | 87.3 | αro-αw3o | 1 422 | 84.4 | αro-αw2w3 | 1 422 | 82.1 | αrx-αrγ | 598 | 73.6 | |||
| αro-αw3x | 579 | 87.0 | αrw2-αoγ | 1 422 | 84.4 | αrw3-αrx | 582 | 82.0 | αrx-αoγ | 592 | 72.8 | |||
| αrw1-αw3o | 1 422 | 86.8 | αw1w2-αw3o | 2 045 | 84.4 | αrw3-αoγ | 1 422 | 81.8 | αw2o-αw2x | 842 | 72.7 | |||
| αro-αox | 592 | 86.7 | αw1w3-αw2o | 2 045 | 84.4 | αw1γ-αw2w3 | 2 082 | 81.8 | αw2o-αox | 842 | 72.6 | |||
| αw1w3-αox | 842 | 86.7 | αrw2-αw1w3 | 1 450 | 84.3 | αw2w3-αoγ | 2 045 | 81.8 | αrx-αw2γ | 582 | 72.3 | |||
| αw1w3-αw1x | 845 | 86.7 | αrγ-αw1γ | 1 450 | 84.3 | αw2w3-αw3o | 2 045 | 81.8 | αw2x-αxγ | 845 | 72.3 | |||
| αrx-αox | 592 | 86.5 | αro-αw1w2 | 1 422 | 84.2 | αrx-αw3x | 582 | 81.6 | αrx-αw3o | 579 | 72.0 | |||
| αw1w2-αxγ | 845 | 86.5 | αrx-αw1w3 | 582 | 84.2 | αrw3-αw1γ | 1 450 | 81.5 | αw1γ-αoγ | 2 045 | 71.7 | |||
| αw1w3-αw2x | 845 | 86.4 | αw1o-αw3o | 2 045 | 84.2 | αw1γ-αw3o | 2 045 | 81.5 | αw1x-αw2o | 842 | 71.3 | |||
| αw1w2-αw1o | 2 045 | 86.3 | αw1w3-αw1o | 2 045 | 84.2 | αw2w3-αw2γ | 2 082 | 81.5 | αw1x-αw1γ | 845 | 71.2 | |||
| αw1w3-αw3x | 845 | 86.2 | αrw1-αrw2 | 1 450 | 84.1 | αw2w3-αw3γ | 2 082 | 81.5 | αw2o-αw3x | 842 | 71.1 | |||
| αrw1-αw2o | 1 422 | 86.1 | αrw1-αw2γ | 1 450 | 84.1 | αrw3-αw3x | 582 | 81.1 | αw2x-αw2γ | 845 | 71.0 | |||
| αrx-αw1w2 | 582 | 86.1 | αrw1-αw3γ | 1 450 | 84.1 | αw1x-αw3o | 842 | 81.1 | αw2γ-αxγ | 845 | 70.3 | |||
| αw1w2-αw2o | 2 045 | 86.1 | αw1w3-αoγ | 2 045 | 84.1 | αrw3-αw2o | 1 422 | 81.0 | αw2γ-αoγ | 2 045 | 70.2 | |||
| αrw2-αw3o | 1 422 | 85.9 | αw1w3-αw1γ | 2 082 | 84.1 | αrw3-αw2γ | 1 450 | 80.5 | αw1x-αxγ | 845 | 70.1 | |||
| αw1w3-αxγ | 845 | 85.9 | αw1w3-αw2γ | 2 082 | 84.1 | αw2x-αw3o | 842 | 80.5 | αw1γ-αox | 842 | 69.7 | |||
| αrx-αw1x | 582 | 85.7 | αw1w3-αw3o | 2 045 | 84.1 | αrw3-αxγ | 582 | 80.4 | αw2o-αw2γ | 2 045 | 69.7 | |||
| αro-αxγ | 592 | 85.5 | αw1w3-αw3γ | 2 082 | 84.1 | αw3o-αw3x | 842 | 80.2 | αw3x-αxγ | 845 | 69.1 | |||
| αrw1-αox | 579 | 85.5 | αrw1-αrγ | 1 450 | 84.0 | αrw3-αox | 579 | 80.1 | αrγ-αw1o | 1 422 | 69.0 | |||
| αrw1-αro | 1 422 | 85.5 | αrw1-αw1γ | 1 450 | 84.0 | αrw3-αw2x | 582 | 80.1 | αw3o-αoγ | 2 045 | 68.9 | |||
| αw1o-αw2o | 2 045 | 85.5 | αw2w3-αxγ | 845 | 84.0 | αrw3-αw3γ | 1 450 | 80.0 | αw3x-αw3γ | 845 | 68.9 | |||
| αro-αw1o | 1 422 | 85.4 | αw1w3-αw2w3 | 2 082 | 83.9 | αrw3-αrγ | 1 450 | 79.9 | αw1o-αw3x | 842 | 68.1 | |||
| αw1w2-αoγ | 2 045 | 85.3 | αro-αw2γ | 1 422 | 83.8 | αrγ-αw3γ | 1 450 | 79.9 | αw3γ-αxγ | 845 | 67.6 | |||
| αrw1-αw1w2 | 1 450 | 85.2 | αrw1-αrw3 | 1 450 | 83.8 | αw3x-αoγ | 842 | 79.9 | αw1x-αw2γ | 845 | 67.0 | |||
| αrw1-αw1x | 582 | 85.2 | αrw2-αox | 579 | 83.8 | αrw3-αw1o | 1 422 | 79.8 | αw2x-αox | 842 | 67.0 | |||
| αw1w2-αw1w3 | 2 082 | 85.2 | αrw2-αw1o | 1 422 | 83.8 | αrγ-αw2w3 | 1 450 | 79.8 | αw1o-αox | 842 | 65.9 | |||
| αw1x-αw2w3 | 845 | 85.2 | αrw2-αw3γ | 1 450 | 83.8 | αw3o-αox | 842 | 79.8 | αw2γ-αox | 842 | 65.8 | |||
| αrw1-αoγ | 1 422 | 85.1 | αrw1-αw2w3 | 1 450 | 83.7 | αw3x-αox | 842 | 79.8 | αw3o-αw3γ | 2 045 | 65.5 | |||
| αrw1-αw1o | 1 422 | 85.1 | αrw2-αw2x | 582 | 83.7 | αw2γ-αw3o | 2 045 | 79.3 | αw1x-αw3γ | 845 | 65.4 | |||
| αrw1-αw2x | 582 | 85.1 | αrw3-αw2w3 | 1 450 | 83.7 | αrw3-αw1x | 582 | 79.2 | αw2x-αw3γ | 845 | 65.4 | |||
| αrw3-αw1w2 | 1 450 | 85.1 | αrw2-αrγ | 1 450 | 83.6 | αrγ-αw2x | 582 | 79.2 | αrγ-αw2o | 1 422 | 65.1 | |||
| αw1w2-αw2w3 | 2 082 | 85.1 | αrw2-αrw3 | 1 450 | 83.5 | αrγ-αw3x | 582 | 79.2 | αw3γ-αox | 842 | 64.7 | |||
| αro-αrx | 592 | 85.0 | αro-αw1w3 | 1 422 | 83.3 | αrx-αw1γ | 582 | 79.0 | αw2o-αxγ | 842 | 64.5 | |||
| αrw2-αw1w2 | 1 450 | 85.0 | αrw2-αw1x | 582 | 83.3 | αrγ-αw1x | 582 | 78.5 | αw1x-αox | 842 | 64.4 | |||
| αw1w2-αw1γ | 2 082 | 85.0 | αrw3-αro | 1 422 | 83.3 | αw1x-αoγ | 842 | 78.1 | αw1o-αw2x | 842 | 63.8 | |||
| αw1w2-αw2γ | 2 082 | 85.0 | αw1o-αw2w3 | 2 045 | 83.3 | αoγ-αxγ | 859 | 77.5 | αw2o-αw3γ | 2 045 | 62.6 | |||
| αw1w2-αw3γ | 2 082 | 85.0 | αw2γ-αw3γ | 2 082 | 83.3 | αox-αoγ | 859 | 77.1 | αw1o-αxγ | 842 | 61.4 | |||
| αw1γ-αw3γ | 2 082 | 85.0 | αro-αw3γ | 1 422 | 83.2 | αw1γ-αw2o | 2 045 | 76.8 | αw3o-αxγ | 842 | 59.6 | |||
| αrw2-αro | 1 422 | 84.9 | αrγ-αw1w2 | 1 450 | 83.2 | αw1o-αoγ | 2 045 | 76.7 | αw1o-αw3γ | 2 045 | 56.9 | |||
| αrw3-αw1w3 | 1 450 | 84.9 | αro-αrγ | 1 451 | 83.1 | αrx-αw1o | 579 | 76.2 | αrγ-αw3o | 1 422 | 54.2 | |||
| αw2w3-αw3x | 845 | 84.9 | αrw2-αw1γ | 1 450 | 83.1 | αw1o-αw1γ | 2 045 | 76.1 | αw1o-αw2γ | 2 045 | 50.6 | |||
| αrw2-αw2o | 1 422 | 84.8 | αrw2-αw2w3 | 1 450 | 83.1 | αrγ-αox | 592 | 75.7 | αw1o-αw1x | 842 | 40.0 | |||
| αw1γ-αw2γ | 2 082 | 84.8 | αrw2-αw2γ | 1 450 | 83.1 | αrx-αw2o | 579 | 75.1 | αrx-αw3γ | 582 | 39.0 | |||
| αw2w3-αox | 842 | 84.8 | αrγ-αoγ | 1 451 | 83.1 | αw1γ-αxγ | 845 | 75.1 | ||||||
| αro-αw2o | 1 422 | 84.7 | αrw2-αxγ | 582 | 83.0 | αw1γ-αw2x | 845 | 74.8 |
我们计算了21个光谱指数,并分析他们的分布情况。在宽波段谱指数分布图(图 1~图 2)中,我们发现有微弱双峰分布的宽波段谱指数一共有9个,其中8个明显区分耀变体的两个亚类(如图 3)。耀变体是一种宽波段非热辐射源,从无线电波长一直延伸到高能γ射线[22]。耀变体具有典型的双峰谱能量分布,其中的低能峰为同步辐射峰。耀变体两个亚类的光谱能量分布中,同步辐射峰的峰值功率与峰值频率存在反相关关系[6],因此,与光谱能量分布峰值有关的多波段复合光谱指数构建的谱指数以及谱指数平面可以作为耀变体亚类的分类器。
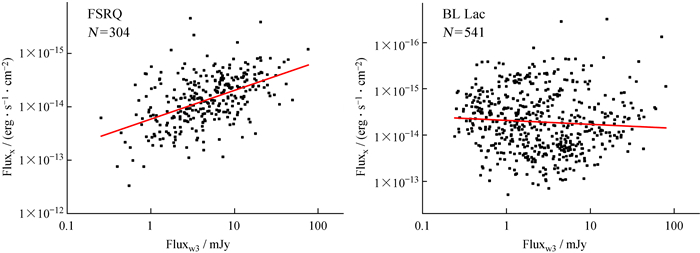
如表 3,21个谱指数两两组合一共有210种谱指数-谱指数图。基于谱指数-谱指数图的支持向量机,我们计算了他们的分类准确率。从中我们发现αw1x-αw3x平面分类的准确率最高(见表 3)。为此,我们进一步研究了w3波段与X射线的流量相关性,发现这两个波段的流量关系对于耀变体的两个子类有明显的不同。如图 5,平谱射电类星体的w3波段与X射线的流量相关系数为0.50,表明相关性很强,但也可以看到数据点有较大的弥散,我们收集的数据的不同时性可能是数据弥散的原因之一;而蝎虎座BL型天体的相关系数为-0.07,相关系数几乎为零,即没有相关性。这个相关性分析也支持X射线辐射机制的不同可能是区分平谱射电类星体和蝎虎座BL型天体的主要物理原因。
|
| 图 5 红外波段w3与X-ray波段的流量之间的相关性 Fig. 5 The correlation between infrared w3 and X-ray fluxes |
本文以最新版的费米4期目录为主要样本,通过斯特拉斯堡天文台的数据库对其进行了多波段巡天数据的交叉匹配,得到多波段流量数据,进而计算了21种宽波段谱指数。在此基础上发现耀变体的8个宽波段谱指数分布具有双峰结构,且能比较明显地区分耀变体的两个亚类。通过机器学习中的支持向量机模型,我们进一步分析了210个谱指数平面对耀变体亚类的分类准确率,发现大部分准确率在80%以上。宽波段谱指数及谱指数平面的耀变体分类作用可能与耀变体亚类同步辐射特征的不同有关,比如平谱射电类星体的光谱能量分布同步峰值频率总体上比蝎虎座BL型天体的小。
| [1] | URRY C M, PADOVANI P. Unified schemes for radio-loud active galactic nuclei[J]. Publications of the Astronomical Society of the Pacific, 1995, 107(715): 803–845. |
| [2] | GHISELLINI G, CELOTTI A. The dividing line between FR Ⅰ and FR Ⅱ radio-galaxies[J]. Astronomy & Astrophysics, 2001, 379: L1. |
| [3] | JESTER S. A simple test for the existence of two accretion modes in active galactic nuclei[J]. The Astrophysical Journal, 2005, 625(2): 667–679. DOI: 10.1086/429812 |
| [4] | GHISELLINI G, MARASCHI L, TAVECCHIO F. The Fermi blazars' divide[J]. Monthly Notices of the Royal Astronomical Society, 2009, 396(1): L105. DOI: 10.1111/j.1745-3933.2009.00673.x |
| [5] | BHATTACHARYA D, SREEKUMAR P, MUKHOPADHYAY B, et al. Does black hole spin play a key role in the FSRQ/BL Lac dichotomy?[J]. Research in Astronomy and Astrophysics, 2016, 16(4): 54. |
| [6] | FOSSATI G, MARASCHI L, CELOTTI A, et al. A unifying view of the spectral energy distributions of blazars[J]. Monthly Notices of the Royal Astronomical Society, 1998, 299(2): 433–448. DOI: 10.1046/j.1365-8711.1998.01828.x |
| [7] | ACKERMANN M, AJELLO M, ATWOOD W B, et al. The third catalog of active galactic nuclei detected by the Fermi large area telescope[J]. The Astrophysical Journal, 2015, 810(1): 14. DOI: 10.1088/0004-637X/810/1/14 |
| [8] | AJELLO M, ANGIONI R, AXELSSON M, et al. The fourth catalog of active galactic nuclei detected by the Fermi large area telescope[J]. The Astrophysical Journal, 2020, 892(2): 105. DOI: 10.3847/1538-4357/ab791e |
| [9] | ABDOLLAHI S, ACERO F, BALDINI L, et al. Incremental Fermi large area telescope fourth source catalog[J]. The Astrophysical Journal Supplement Series, 2022, 260(2): 53. DOI: 10.3847/1538-4365/ac6751 |
| [10] | LEDDEN J E, O'DELL S L. The radio-optical-X-ray spectral flux distributions of blazars[J]. The Astrophysical Journal, 1985, 298(2): 630–643. |
| [11] | CHIARO G, SALVETTI D, LA MURA G, et al. Blazar flaring patterns (B-FlaP) classifying blazar candidate of uncertain type in the third Fermi-LAT catalogue by artificial neural networks[J]. Monthly Notices of the Royal Astronomical Society, 2016, 462(3): 3180–3195. DOI: 10.1093/mnras/stw1830 |
| [12] | IVEZIĆ Ž, CONNOLLY A J, VANDERPLAS J T, et al. Statistics, data mining, and machine learning in astronomy: a practical Python guide for the analysis of survey data[M]. Princeton: Princeton University Press, 2014: 382-405. |
| [13] | BALL N M, BRUNNER R J. Data mining and machine learning in astronomy[J]. International Journal of Modern Physics D, 2010, 19(7): 1049. DOI: 10.1142/S0218271810017160 |
| [14] | HASSAN T, MIRABAL N, CONTRERAS J L, et al. Gamma-ray active galactic nucleus type through machine-learning algorithms[J]. Monthly Notices of the Royal Astronomical Society, 2013, 428(1): 220–225. DOI: 10.1093/mnras/sts022 |
| [15] | ARSIOLI B, DEDIN P. Machine learning applied to multifrequency data in astrophysics: blazar classification[J]. Monthly Notices of the Royal Astronomical Society, 2020, 498(2): 1750. DOI: 10.1093/mnras/staa2449 |
| [16] |
朱惊天, 樊军辉, 蔡金庭. 罗马5期耀变体多波段目录BZUs的分类[J]. 天文研究与技术, 2021, 18(1): 25–42 ZHU J T, FAN J H, CAI J T. Classfication for BZUs in 5BZCAT[J]. Astronomical Research & Technology, 2021, 18(1): 25–42. |
| [17] | LI H Z, XIE G Z, YI T F, et al. The spectral energy distributions of the Fermi blazars and connection among low-energy peaked BL Lacertae, high-energy peaked BL Lacertae, and flat spectrum radio quasars[J]. The Astrophysical Journal, 2010, 709(2): 1407–1411. DOI: 10.1088/0004-637X/709/2/1407 |
| [18] | CHEN L E, LI H Z, YI T F, et al. The spectral properties of Fermi blazars: the spectral sequence and unification of blazars[J]. Research in Astronomy and Astrophysics, 2013, 13(1): 5. DOI: 10.1088/1674-4527/13/1/002 |
| [19] | LI H Z, CHEN L E. Spectral energy distributions of SDSS blazars[J]. Journal of Astrophysics and Astronomy, 2014, 35(3): 387–389. DOI: 10.1007/s12036-014-9237-5 |
| [20] | LI H Z, CHEN L E, JIANG Y G, et al. The broadband spectral energy distributions of SDSS blazars[J]. Research in Astronomy and Astrophysics, 2015, 15(7): 929. DOI: 10.1088/1674-4527/15/7/001 |
| [21] | YI T F, ZHANG J, LU R J, et al. Evaluating optical classification for Fermi blazar candidates with a statistical method using broadband spectral indices[J]. The Astrophysical Journal, 2017, 838(1): 34. DOI: 10.3847/1538-4357/aa63f5 |
| [22] | PADOVANI P, ALEXANDER D M, ASSEF R J, et al. Active galactic nuclei: what's in a name?[J]. Astronomy and Astrophysics Review, 2017, 25(1): 2. |



