2. 宝鸡文理学院电子电气工程学院, 陕西 宝鸡 721016;
3. 江苏师范大学圣理工学院, 江苏 徐州 221116
2. School of Electrical and Electronic Engineering, Baoji University of Arts and Sciences, Baoji 721016, China;
3. JSNU SPBPU institute of Engineering, Xuzhou 221116, China
由于地球周围的对流层对电磁波的折射效应,电磁波信号的传播速度变慢,传播路径弯曲,导致电磁波信号传播延迟,这种现象称为对流层延迟。对流层延迟可以分为静力学延迟(也称对流层干延迟,Zenith Hydrostatic Delay (ZHD))与非静力学延迟(又称对流层湿延迟,Zenith Wet Delay (ZWD)),其中,对流层干延迟由大气中的干燥气体引起,占总延迟的90%左右,变化比较稳定;对流层湿延迟由水汽引起,占总延迟的10%左右,具有时变性。在对流层延迟改正中,通常将电磁波信号在天顶方向的延迟通过映射函数投影至传播路径,从而对对流层倾斜延迟予以改正。对流层延迟的大小与卫星高度角有关,在天顶方向延迟约为2 m,在地平方向可达20 m[1],因此,对流层延迟是全球卫星导航系统(Global Navigation Satellite System, GNSS)和甚长基线干涉测量(Very Long Baseline Interferometry, VLBI)等空间大地测量技术的重要误差源之一[2-3]。
对流层是非色散介质, 无法采用频率组合的方式消除对流层延迟,通常用对流层延迟经验模型予以修正。当前常用的对流层天顶延迟经验模型大致可以分为两类,一类是基于实测气象参数的Saastamoinen和Hopfield等模型,另一类是仅需测站地理位置信息的非气象参数模型,如美国广域增强系统(Wide Area Augmentation System, WAAS)采用的UNB模型[4]和欧洲广域增强系统采用的EGNOS模型[5]。基于实测气象参数的对流层天顶延迟模型的改正效果高度依赖于实测地表气象参数,利用实测地表气象参数估计对流层天顶延迟,改正精度可达厘米级[6],若利用标准气象参数则改正效果较差,这限制了此类模型在实时定位、导航与授时中的推广应用。Saastamoinen和Hopfield等模型对对流层天顶延迟处理比较简单,对流层天顶延迟改正精度难以有较大提高;UNB系列模型和EGNOS模型无需实测地表气象参数,使用简便,它们的全球平均对流层天顶延迟改正精度可以与基于实测气象参数的Saastamoinen和Hopfield模型相当。然而,由于这些模型将大地按15°的纬度等间隔划分,分辨率较差,且忽略经度的影响,导致这些模型无法细致地刻画对流层延迟的局部变化,在某些区域的改正效果不佳[7]。
考虑到现有对流层天顶延迟经验模型的局限性,采用与实测气象参数相符合的气象参数模型估计对流层天顶延迟成为改善对流层天顶延迟改正效果的一种有效方法,近年来得到了广泛应用[8-10]。文[8]利用GPT与UNB3m气象参数模型估计的气温、大气压和水汽压参数作为Saastamoinen模型的输入,有效提高了Saastamoinen模型的适用性;文[1]利用GPT2模型提供的气温、大气压和相对湿度应用于Saastamoinen模型估计对流层天顶延迟,建立了适用于全球范围的对流层天顶延迟精化模型;文[9-10]通过GPT2w模型计算气象参数,并分别将气象参数作为Hopfield和Saastamoinen模型的输入,摆脱了Saastamoinen和Hopfield模型对实测气象参数的依赖,提高了两种经典模型的普适性。总结已有的研究发现,通过GPT, GPT2, GPT2w和UNB3m模型能够提高Hopfield和Saastamoinen模型的适用性,但由于它们的湿延迟估计精度较差,限制了两种经典模型对流层天顶延迟估计精度的进一步提高。此外,不同气象参数模型在不同区域具有一定的适用性。
为进一步提高基于气象参数的对流层天顶延迟模型的改正精度,本文在上述研究的基础上,将目前最新的GPT系列模型——GPT3模型提供的气象参数应用于对流层天顶延迟计算,其中,采用Saastamoinen模型估计对流层干延迟,采用性能更好的Askne模型估计对流层湿延迟,Saastamoinen模型所需的气压和Askne模型所需的水汽压、大气加权平均温度与水汽垂直递减率4个关键气象参数均由1°×1°空间分辨率的GPT3模型提供,由此构成Sas+Ask+GPT3融合模型。考虑到GPT3模型在亚洲区域的对流层天顶延迟估计中应用较少,本文以GGOS Atmosphere和IGS发布的对流层天顶延迟产品作为参考,分析评估了组合模型和同等条件下的Sas+GPT3和Sas+Ask+UNB3m应用于亚洲区域的对流层天顶延迟改正精度,并分析了模型误差的时空分布特征。研究结果表明,GPT3模型提供的气象参数相对更符合亚洲区域的实际情况,Sas+Ask+GPT3融合模型对流层天顶延迟的估计精度总体最优,可应用于亚洲区域的对流层天顶延迟的实时改正,并具有所需参数少和使用方便的优点。
1 多模型融合对流层天顶延迟估计方法Saastamoinen和Hopfield模型是两种应用广泛的对流层天顶延迟经验模型,其中,前者精度受高程影响很小,而后者精度随高程的增加而降低,故Saastamoinen模型的适用范围更广[6],但Saastamoinen模型对对流层湿延迟处理较为简单,估计误差较大。Askne模型融入大气加权平均温度和水汽垂直递减率参数[11],对流层湿延迟估计精度更高,但这些参数依赖于探空气球测量,限制了其在对流层天顶延迟实时改正中的应用。GPT3模型在GPT2w模型的基础上引入梯度算法,进一步优化了模型性能,可以提供全球范围内1°×1°高分辨率的气象参数[12]。为提高对流层天顶延迟经验模型的估计精度和适应能力,本文提出一种多模型融合的对流层天顶延迟估计方法,分别采用Saastamoinen和Askne模型估计对流层干延迟和湿延迟,两种模型所需的气象参数全部由GPT3模型提供,在提高对流层天顶延迟估计精度的同时实现对流层天顶延迟的实时改正。
1.1 Saastamoinen模型Saastamoinen模型将对流层分为两层进行积分,第1层为从地表到10 km高度的对流层顶,该层的温度变化率为6.5 ℃/km;第2层为从10 km到50 km高度的平流层顶,该层的温度视为常数。Saastamoinen模型首次将被积函数按照天顶距三角函数展开逐项进行积分,并把对流层天顶延迟分为对流层干延迟和湿延迟两个分量之和,两个分量的表达式为
| $ \left\{\begin{array}{l} Z H D=\frac{0.002277 P}{f(\varphi, h)} \\ Z W D=\frac{0.002277 e}{f(\varphi, h)}\left(0.05+\frac{1255}{T}\right)\;, \\ f(\varphi, h)=1-0.00266 \cos (2 \varphi)-0.00028 h \end{array}\right. $ | (1) |
其中,P, T, e, φ和h分别为地表气压(hPa)、地表温度(K)、水汽压(hPa)、测站纬度(rad)和高程(km)。
1.2 Askne模型Askne模型融入大气加权平均温度和水汽垂直递减率参数,以改善对流层湿延迟估计精度,对流层湿延迟的表达式为[11]
| $ Z W D=10^{-6}\left(k_2^{\prime}+\frac{k_3}{T_{\mathrm{m}}}\right) \frac{R_{\mathrm{d}} e}{(\lambda+1) g_{\mathrm{m}}}, $ | (2) |
其中,Tm为大气加权平均温度(K);λ为水汽垂直递减率(hPa/m);gm为重力加速度,gm=9.806 65 m/s2;k′2=16.52 K/hPa;k3=3.776×105 K2/hPa;Rd=287.053 8 J /(K·g)。
1.3 GPT3模型GPT系列模型是Boehm等利用欧洲中尺度天气预报中心(European Centre for Medium-Range Weather Forecasts, ECMWF)长期的再分析气象资料建立的全球气象参数经验模型,仅需知道测站地理位置信息与年积日便可以获得地表温度、大气压力和水汽压等气象参数,在全球范围内得到广泛应用。GPT3模型是GPT系列模型的最新版本,它在GPT2w模型的基础上引入梯度算法以进一步优化模型,可以提供1°×1°空间分辨率的格网气象参数。格网点气象参数的计算公式为[12]
| $ \xi=A_0+A_1 \cos \left(\frac{d o y}{365.25} 2 \pi\right)+B_1 \sin \left(\frac{d o y}{365.25} 2 \pi\right)+A_2 \cos \left(\frac{d o y}{365.25} 4 \pi\right)+B_2 \sin \left(\frac{d o y}{365.25} 4 \pi\right), $ | (3) |
其中,ξ为格网点气象参数;doy为年积日;A0为气象参数的平均值;A1和B1为气象参数的年周期振幅;A2和B2为气象参数的半年周期振幅。
1.4 融合模型针对Saastamoinen和Askne模型对实测气象参数的依赖性,本文提出一种适用于亚洲区域的对流层天顶延迟融合估计模型。该模型融合GPT3提供的大气压力、地表温度和水汽压等高精度气象参数来优化对流层干延迟和湿延迟估计所需的气象参数,从而克服对实测气象参数的依赖,提高对流层干延迟和湿延迟估计精度,同时实现对流层天顶延迟的实时改正。融合模型的对流层天顶延迟计算步骤为(1) 根据测站经度、纬度、高程和年积日信息计算距离测站邻近的4个格网点的气压、温度、水汽压、水汽垂直递减率和大气加权平均温度气象参数,并利用(4)~(7) 式将格网点上的气压、温度、水汽压进行高程修正,将其归算为测站高程上的格网点参数;(2) 将测站高程上4个格网点参数的气象参数进行双线性插值,获得测站位置的气象参数;(3) 将插值得到的气象参数代入模型,计算对流层干延迟和湿延迟,
| $ \left\{\begin{array}{l} P=P_0 \exp \left[-g_m \mathrm{~d} M_{t r} /\left(R_g T_v\right)\right] / 100 \\ T_v=T_0(1+0.6077 Q) \end{array}, \right. $ | (4) |
| $ T = {T_0} + {\rm{d}}T{\rm{d}}h, $ | (5) |
| $ e=Q P /(0.622+0.378 Q), $ | (6) |
其中,P0和T0分别为格网点上的气压(hPa)和温度(K);dT为温度垂直递减率;Q为比湿;dh为高程修正量(m);dMtr和Rg分别为大气摩尔质量与气体常数,dMtr=0.028 965 kg/mol,Rg=8.314 3 J /(K·mol),其他参数含义同上。
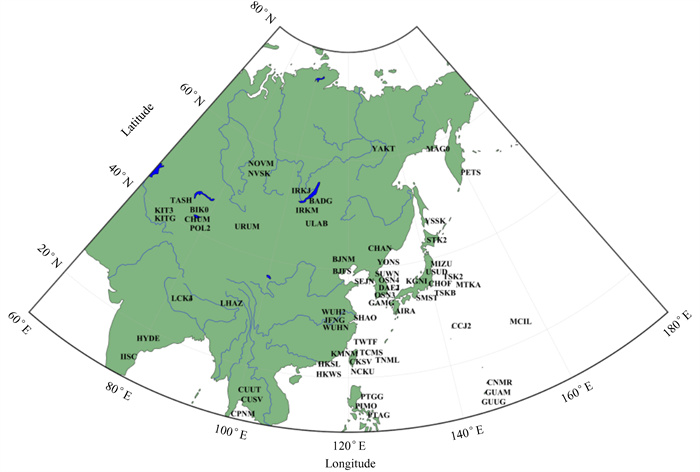
2 精度评定方法 2.1 研究区域亚洲地域跨度大,气候复杂多变,为验证融合模型在亚洲区域的对流层天顶延迟改正的有效性,本文选取亚洲区域66个IGS站分析评估对流层天顶延迟的改正效果,这些测站具备地域跨度大、海拔与气候差异明显等特点,研究区域的范围为10 °N~63 °N,66 °E~159 °E,选取的亚洲区域66个IGS站的地理分布如图 1,各IGS站的经纬度和高程数值可通过 https://igs.org/network/#new-site-checklist查询,限于篇幅,在此不再列出。
|
| 图 1 亚洲区域IGS站点分布 Fig. 1 Distribution of the selected IGS stations over Asia |
GGOS Atmosphere和IGS提供的对流层天顶延迟产品具有很高的质量,可以作为对流层天顶延迟研究与应用的标准数据。本文利用这两种对流层天顶延迟产品作为参考值对融合模型的精度进行分析评估,其中,GGOS Atmosphere基于ECMWF 40a再分析资料,可以提供1979年至今空间分辨率为2.5 °× 2 ° (经度×纬度)、时间分辨率为6 h (每天0:00,6:00,12:00和18:00) 的全球对流层天顶延迟格网数据,数据可以从 https://vmf.geo.tuwien.ac.at获取;IGS提供的全球对流层天顶延迟数据由GNSS解算,时间分辨率为5 min,数据可以从 https://cddis.nasa.gov获取。本文选取2016~2018年的对流层天顶延迟产品作为参考,分析评估了融合对流层天顶延迟模型误差的时空分布特征。
2.3 精度评定指标本文分别以GGOS Atmosphere和IGS发布的对流层天顶延迟产品作为参考值,选取平均偏差(bias)与均方根误差(RMS)两个指标对不同模型的对流层天顶延迟估计结果进行分析评估,其计算公式分别为
| $ {\rm{ }}bias{\rm{ }} = \frac{1}{N}\sum\limits_{i = 1}^N {\left( {ZTD_i^{\rm{p}} - ZTD_i^{\rm{o}}} \right)} , $ | (7) |
| $ R M S=\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left(Z T D_i^{\mathrm{p}}-Z T D_i^{\mathrm{o}}\right)^2}, $ | (8) |
其中,ZTDip为模型计算值;ZTDio为GGOS Atmosphere和IGS提供的对流层天顶延迟数据;N为对流层天顶延迟数据的样本个数。
3 模型验证为更好地分析评估Sas+Ask+GPT3融合模型在亚洲区域对流层天顶延迟改正的有效性,在固定GPT3模型的条件下与Saastamoinen模型形成Sas+GPT3模型,其中,干、湿延迟均利用Saastamoinen模型计算,所需参数由GPT3模型提供;在固定Sas+Ask模型的条件下与UNB3m模型形成Sas+Ask+UNB3m模型,其中,干、湿延迟分别利用Saastamoinen和Askne模型计算,所需参数由UNB3m模型提供,并将本文融合模型与另外两种模型的对流层天顶延迟估计误差进行对比分析。
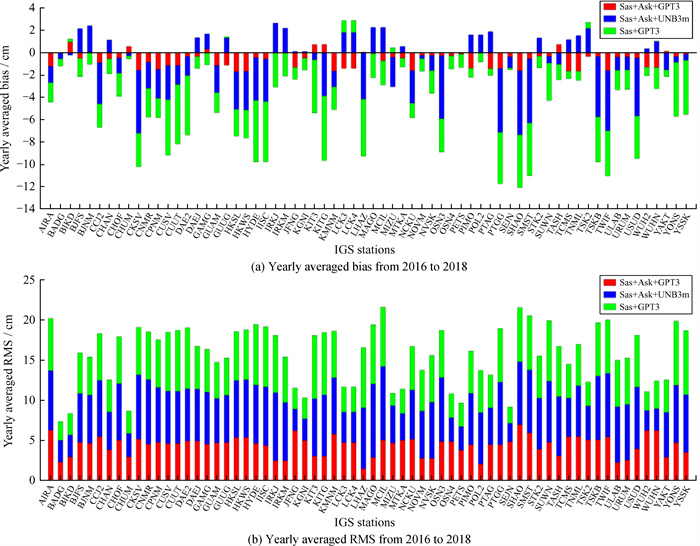
3.1 平均偏差和均方根误差统计结果我们分别以GGOS Atmosphere和IGS发布的2016~2018年对流层天顶延迟数据作为参考,计算3种融合模型2016~2018年66个IGS站的平均偏差与均方根误差,如图 2和图 3,66个IGS站的平均偏差与均方根误差统计结果见表 1。
|
| 图 2 相对GGOS Atmosphere产品的对流层天顶延迟估计平均偏差与均方根误差 Fig. 2 Bias and RMS between the ZTD estimates and GGOS Atmosphere products |
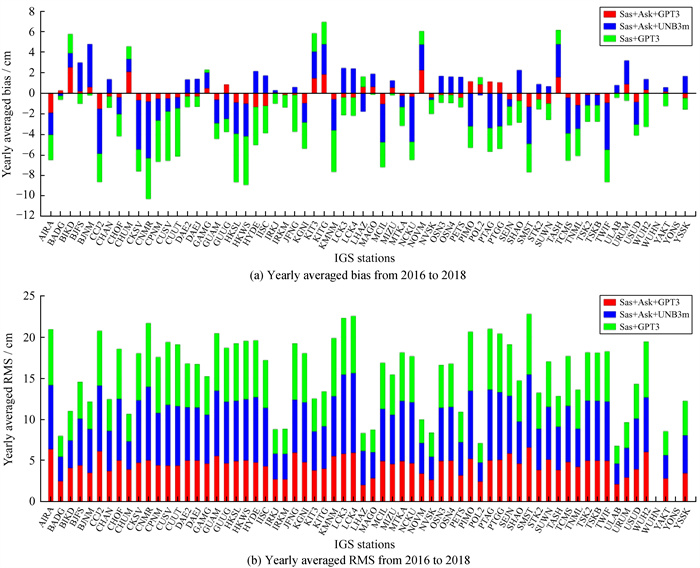
|
| 图 3 相对IGS产品的对流层天顶延迟估计平均偏差与均方根误差 Fig. 3 Bias and RMS between the ZTD estimates and IGS products |
| Reference data | Sas+Ask+ GPT3 | Sas+Ask+ UNB3m | Sas+GPT3 | |||||
| bias | RMS | bias | RMS | bias | RMS | |||
| GGOS Atmosphere | -0.61 | 4.35 | -1.04 | 6.09 | -2.16 | 5.37 | ||
| IGS | -0.35 | 4.53 | -0.20 | 6.03 | -1.59 | 5.27 | ||
由表 1可知,以GGOS Atmosphere产品为参考时,Sas+Ask+GPT3模型的平均偏差相对同等条件下的Sas+Ask+UNB3m和Sas+GPT3模型分别降低约41%和72%,均方根误差分别降低约29%和19%;以IGS对流层天顶延迟产品为参考时,Sas+Ask+GPT3模型的均方根误差相对另两种模型分别降低约25%和14%,平均偏差相对Sas+GPT3模型降低约78%,但其平均偏差大于同等条件下的Sas+Ask+UNB3m模型。由图 2 (a)和图 3(a)可以看到,无论是以GGOS Atmosphere还是IGS对流层天顶延迟数据为标准,3种模型的平均偏差均存在很多负值,导致66个IGS站的平均偏差也为负值;Sas+Ask+UNB3m模型的平均偏差为负值的情况少于Sas+Ask+GPT3和Sas+GPT3模型,特别是在以IGS对流层天顶延迟产品为参考时,该模型在39个IGS站的平均偏差为负值,27个站为正值,而另两种模型在大部分IGS站为负值,导致根据(7) 式计算的Sas+Ask+UNB3m模型的平均偏差偏小;图 2和图 3还显示3种模型在局部水汽丰富且变化复杂的区域均出现较大偏差(如HKSL, WUHN和SHAO等IGS附近区域),但Sas+Ask+GPT3模型的精度相对最优,说明Sas+Ask+GPT3模型效果明显。
Sas+Ask+GPT3和Sas+Ask+UNB3m模型相当于在固定对流层天顶延迟模型的条件下与不同气象参数模型形成的融合模型,而Sas+Ask+GPT3和Sas+GPT3模型相当于在固定气象参数模型的条件下与不同对流层天顶延迟模型形成的融合模型,故Sas+Ask+GPT3模型在同等条件下与另两种模型进行对比。Sas+Ask+GPT3模型的对流层天顶延迟改正效果显著优于另两种模型,这一方面说明Askne-ZWD模型的准确性比Saastamoinen-ZWD模型高,另一方面说明GPT3模型在亚洲地区比UNB3m模型具有更好的适应性,这是因为UNB3m模型利用北美地区的探空数据构建而具有一定的区域性。此外,整体而言,Sas+GPT3模型精度高于Sas+Ask+UNB3m模型,说明对流层天顶延迟估计精度不仅和对流层天顶延迟模型的准确性有关,还取决于气象参数的准确性,间接验证了GPT3模型计算气象参数的有效性。本文将对3种模型对流层天顶延迟估计误差的时空变化特征进行分析。
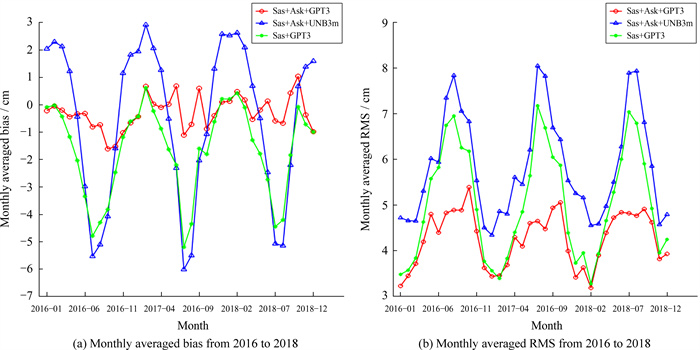
3.2 平均偏差与均方根误差的时间分布特征为分析3种模型平均偏差与均方根误差每日的变化情况,以IGS对流层天顶延迟数据为参考,将2016~2018年66个IGS站的平均偏差和均方根误差月均值进行统计,如图 4。
|
| 图 4 亚洲区域IGS站对流层天顶延迟估计月均平均偏差与均方根误差 Fig. 4 Monthly averaged bias and RMS of the ZTD estimates in the selected IGS stations over Asian |
从图 4可以看到,Sas+Ask+GPT3, Sas+Ask+UNB3m和Sas+GPT3模型的月均平均偏差和均方根误差均表现出显著的季节性变化,月均平均偏差和均方根误差在夏季7月或8月达到最大值,在冬季12月或1月达到最小值,且月均平均偏差和均方根误差在夏季变化幅度相对较大,冬季变化较小,这是由于夏季空气湿度较大,对流层湿延迟变化剧烈,冬季空气比较干燥,对流层湿延迟变化较小,而对流层湿延迟又是对流层天顶延迟估计误差的主项;Sas+Ask+UNB3m模型的月均平均偏差和均方根误差在3种模型中最大,特别是在水汽变化剧烈的夏季,表明UNB3m模型预估的气象参数出现较大偏差;与另两种模型相比,Sas+Ask+GPT3模型的月均平均偏差和均方根误差相对较小,虽然在夏季月份误差增大,但各月份之间变化相对稳定,说明GPT3模型预估的气象参数比UNB3m模型更加准确,同时说明即使在水汽变化复杂的夏季,Askne模型也能较好地反映对流层湿延迟的变化情况。
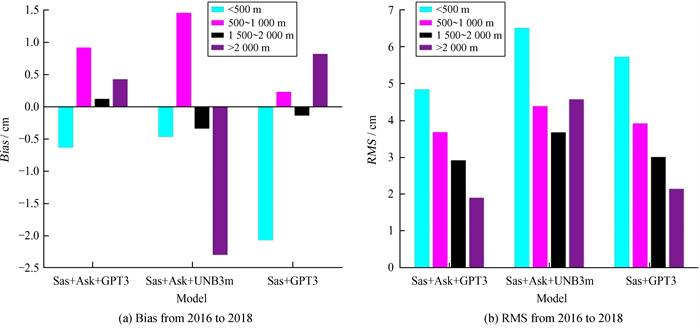
3.3 平均偏差与均方根误差的空间分布特征 3.3.1 平均偏差与均方根误差的高程分布特征亚洲区域地势高,地表起伏大,对流层天顶延迟变化和高程密切相关。为分析3种模型平均偏差与均方根误差在高程上的变化情况,我们将66个站点的高程按0~500 m,500~1 000 m,1 500~2 000 m和>2 000 m进行划分,对2016~2018年各站点的平均偏差与均方根误差进行统计,如图 5,由于在亚洲区域1 000~2 500 m高程范围内无IGS站,故未统计该高程范围内的误差。
|
| 图 5 2016~2018年平均偏差与均方根误差在各高程范围的变化 Fig. 5 Variations of the bias and RMS from 2016 to 2018 with altitude |
由图 5可知,3种模型的平均偏差与高程并无明显关联,但在高程大于2 000 m时Sas+Ask+UNB3m模型的平均偏差较大,可能是在该高程范围内统计的站点个数很少的原因;相反,Sas+Ask+GPT3和Sas+GPT3模型的平均均方根误差与高程有明显规律,即随着高程的增大,两种模型的均方根误差呈现明显的递减趋势,这是因为高海拔地区折射率的积分区间较短,对流层天顶延迟相对较小;Sas+Ask+UNB3m模型在高程0~500 m范围内的均方根误差较大(超过6 cm),当高程大于500 m时均方根误差明显变小(小于5 cm),有递减趋势,但在高程大于2 000 m时均方根误差又突然增大,同样可能是因为此范围内站点很少。另外,从图 5 (a)可以看出,当高程小于500 m时3种模型的平均偏差均为负值,说明在低海拔地区通常低估了对流层天顶延迟。从图中易知,Sas+Ask+GPT3模型在各高程上估计精度均优于另两种模型,特别是对于2 000 m以上的高程,其均方根误差优于2 cm,显著优于同等条件下的Sas+Ask+UNB3m模型。对流层天顶延迟模型易受高程影响的原因在于对流层天顶延迟分布和高度密切相关,且GPT3和UNB3m气象参数模型的高程改正系数精度不同,使得对流层天顶延迟估计精度在不同高程范围内存在一定差异。
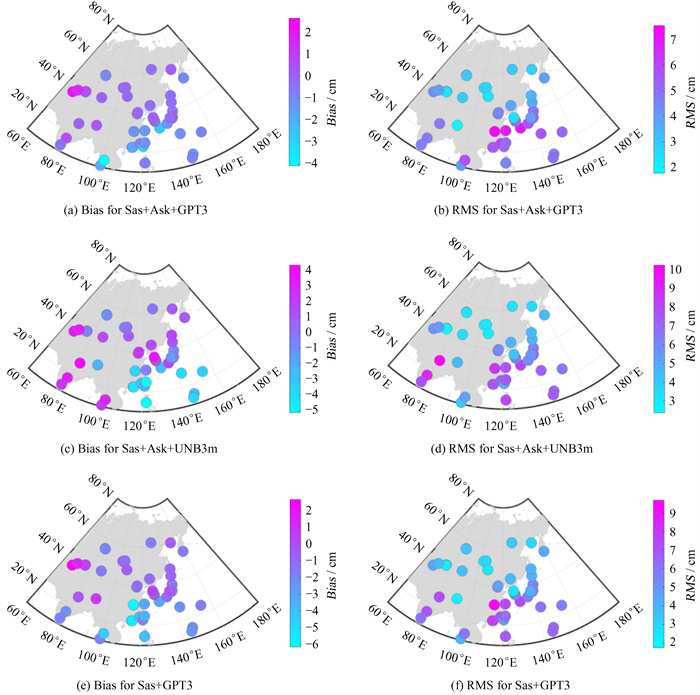
3.3.2 平均偏差与均方根误差的纬度分布特征亚洲区域地貌和地形复杂,海洋与陆地分布比较广泛,气候复杂多样,因此对流层天顶延迟变化也较为复杂。为分析3种模型的平均偏差和均方根误差在亚洲区域的分布情况,图 6给出了平均偏差和均方根误差在各IGS站的分布情况。图 6显示在亚洲南部和东部,3种模型的平均偏差和均方根误差相对较大,而在亚洲南部和西部误差相对较小,特别是在亚洲高纬度地区,Sas+Ask+GPT3模型的平均偏差和均方根误差分别优于0.5 cm和3 cm,因此,在亚洲高纬度区域和西部地区该模型可以应用于高精度对流层天顶延迟研究与应用;在沿海地区的IGS站3种模型的误差通常较大,可能是沿海地区易受海洋气候影响,水汽丰富且变化复杂,导致对水汽估算的精度不足。
|
| 图 6 2016~2018年平均偏差与均方根误差在经纬度上的分布 Fig. 6 Distribution of the bias and RMS from 2016 to 2018 in longitude and latitude |
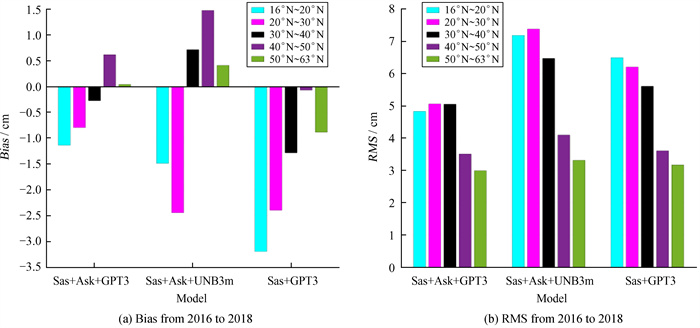
为进一步分析3种模型的平均偏差和均方根误差随纬度的变化情况,我们将纬度按16 °N~20 °N,20 °N~30 °N,30 °N~40 °N,40 °N~50 °N和50 °N~63 °N进行划分,对2016~2018年各纬度范围站点的误差进行统计,如图 7。图 7显示3种模型的均方根误差随着纬度的增加表现出减小的趋势,Sas+Ask+GPT3模型在亚洲各纬度地区相对于另两种模型具有不同程度的改进,特别是在亚洲低纬度地区修正效果更为显著,相对于Sas+Ask+UNB3m和Sas+GPT3m模型,在低于30 °N的低纬度地区,Sas+Ask+GPT3模型的平均偏差分别减少约53%和66%,均方根误差分别降低约32%和22%;在高于30 °N的地区,Sas+Ask+GPT3模型的平均偏差相对于另两种模型降低约99%,均方根误差分别降低约19%和8%。由图 7 (a)还可以看到,在亚洲局部地区UNB3m模型的平均偏差大于文[5]研究得出的0.5 cm的平均偏差,这可能是因为UNB3m模型依据北美地区的探空数据建立而具有一定的区域性。
|
| 图 7 2016~2018年平均偏差与均方根误差在各纬度范围的变化 Fig. 7 Variations of the bias and RMS from 2016 to 2018 with latitude |
为进一步验证Sas+Ask+GPT3模型的效果及时空变化特征的一般性,本文选取位于中国境内的BJFS, CHAN, CKSV, HKSL, LHAZ和WUH2 IGS站2019年1月1日至2019年12月31日的对流层天顶延迟数据对模型精度进行分析评估,这6个IGS站基本覆盖了中国的北部、西部、南部、东北部、东南部和中部区域,具有典型的区域代表性,选取IGS站的信息见表 2 (按高程排序),2019年全年的平均偏差和均方根误差统计结果如表 2。
| Station name | Altitude /m | Latitude /°N | Longitude /°E | Sas+Ask+GPT3 | Sas+Ask+UNB3m | Sas+GPT3 | |||||
| bias | RMS | bias | RMS | bias | RMS | ||||||
| WUH2 | 25.80 | 30.53 | 114.36 | 0.34 | 6.03 | 1.03 | 6.63 | -3.26 | 6.81 | ||
| CKSV | 59.60 | 23.00 | 120.22 | -0.67 | 4.71 | -4.79 | 7.61 | -2.13 | 5.72 | ||
| HKSL | 63.80 | 22.43 | 114.34 | -1.01 | 5.00 | -3.17 | 7.44 | -4.74 | 7.10 | ||
| BJFS | 87.41 | 39.61 | 115.89 | 0.19 | 4.39 | 2.81 | 5.68 | -1.01 | 4.50 | ||
| CHAN | 268.30 | 43.79 | 125.44 | -0.28 | 3.70 | 1.37 | 4.88 | -1.12 | 3.87 | ||
| LHAZ | 3 622.00 | 29.66 | 91.10 | 0.62 | 2.00 | -1.77 | 4.14 | 1.00 | 2.17 | ||
| Average | -0.14 | 4.31 | -0.75 | 6.06 | -1.88 | 5.03 | |||||
表 2显示CKSV和HKSL沿海区域的对流层天顶延迟计算误差较大,这是因为沿海区域易受海洋气候影响,空气潮湿,对流层湿延迟的影响变大,经验模型对水汽预估的精度不足使得对流层湿延迟估计出现较大误差,Sas+Ask+GPT3模型误差明显小于Sas+GPT3模型,表明Ask模型在水汽丰富地区对对流层湿延迟处理更为准确;Sas+Ask+UNB3m模型误差明显大于Sas+Ask+GPT3模型,表明GPT3模型在局部地区估算的气象参数更为准确。由表 2还可以看出,除在HKSL沿海区域外,Sas+Ask+GPT3和Sas+GPT3模型的均方根误差随着高程的增加而减小,BJFS和CHAN中纬度地区的误差小于低纬度地区;相对于Sas+Ask+UNB3m模型,Sas+Ask+GPT3模型的平均偏差和均方根误差分别降低了约82%和29%,相对于Sas+GPT3模型,其平均偏差和均方根误差分别降低了约93%和14%,可以满足中国区域对流层天顶延迟实时修正的应用需求。上述结果表明,Sas+Ask+GPT3模型的修正效果显著,与前述结论相符。
4 结语本文采用传统对流层天顶延迟改正模型的建模思路,将GPT3模型和Saastamoinen, Asknet模型相结合,其中,GPT3模型为后两种模型提供计算对流层干延迟和湿延迟所需的气象参数,由此构成Sas+Ask+GPT3融合模型。我们选取亚洲地区66个IGS站2016~2018年的GGOS Atmosphere和IGS对流层天顶延迟数据对融合模型进行分析评估,结果表明,融合模型在亚洲区域对流层天顶延迟修正效果显著,精度优于同等条件下的Sas+Ask+UNB3m和Sas+GPT3模型,其误差具有夏季大、冬季小的季节性特征,同时模型误差随着IGS站高程或纬度的增加而减小;在水汽变化复杂的地区,Sas+Ask+GPT3模型精度明显优于另两种模型,且在高海拔地区该模型的精度高于Sas+Ask+UNB3m,说明GPT3模型比UNB3m模型在高海拔地区估算的气象参数更为准确。本文利用中国区域6个IGS站2019年的IGS对流层天顶延迟数据对模型进行进一步验证,结果显示,Sas+Ask+GPT3模型的误差特征具有一般性。本文研究表明,融合模型更符合亚洲区域的实际情况,可以用于亚洲地区对流层天顶延迟的实时修正。
| [1] |
姚宜斌, 张豹, 严凤, 等. 两种精化的对流层延迟改正模型[J]. 地球物理学报, 2015, 58(5): 1492–1501 YAO Y B, ZHANG B, YAN F, et al. Single-site improvement and accuracy analysis for zenith tropospheric delays of EGNOS model over Asia area[J]. Chinese Journal of Geophysics, 2015, 58(5): 1492–1501. |
| [2] |
李婷, 童锋贤, 郑为民, 等. GEO卫星的VLBI快速高精度定位观测[J]. 天文研究与技术, 2022, 19(4): 305–316 LI T, TONG F X, ZHENG W M, et al. Fast high accuracy positioning of GEO satellites in VLBI observation[J]. Astronomical Research & Technology, 2022, 19(4): 305–316. |
| [3] |
卢伟俊, 马冠一. 基于神经网络的准实时单站电离层TEC反演[J]. 天文研究与技术, 2022, 19(2): 141–148 LU W J, MA G Y. Near-real-time ionospheric TEC derivation from single station with neural network[J]. Astronomical Research & Technology, 2022, 19(2): 141–148. |
| [4] | PENNA N, DODSON A, CHEN W. Assessment of EGNOS tropospheric correction model[J]. Journal of Navigation, 2001, 54(1): 37–55. DOI: 10.1017/S0373463300001107 |
| [5] | LEANDRO R, SANTOS M C, LANGLEY R B. UNB neutral atmosphere models: development and performance[C]//Proceeding of ION NTM 2006. 2006: 564-573. |
| [6] |
曲伟菁, 朱文耀, 宋淑丽, 等. 三种对流层延迟改正模型精度评估[J]. 天文学报, 2018, 49(1): 113–122 QU W J, ZHU W Y, SONG S L, et al. The evaluation of precision about Hopfield, Saastamoinen and EGNOS tropospheric delays correction model[J]. Acta Astronomica Sinica, 2018, 49(1): 113–122. |
| [7] |
黄良珂, 刘立龙, 文鸿雁, 等. 亚洲地区EGNOS天顶对流层延迟模型单站修正与精度分析[J]. 测绘学报, 2014, 43(8): 808–817 HUANG L K, LIU L L, WEN H Y, et al. Single-site improvement and accuracy analysis for zenith tropospheric delay of EGNOS model over Asia area[J]. Acta Geodaetica Cartographica Sinica, 2014, 43(8): 808–817. |
| [8] |
杨徉, 喻国荣, 潘树国, 等. 一种综合的对流层延迟模型算法[J]. 东南大学学报(自然科学版), 2013, 43(Suppl 2): 418–422 YANG Y, YU G R, PAN S G, et al. A comprehensive algorithm using fusion of tropospheric delay models[J]. Journal of Southeast University (Natural Science Edition), 2013, 43(Suppl 2): 418–422. |
| [9] | LIU J Y, CHEN X H, SUN J Z, et al. An analysis of GPT2/GPT2w+Saastamoinen models for estimating zenith tropospheric delay over Asian area[J]. Advances in Space Research, 2017, 59(3): 824–832. |
| [10] |
杜晓燕, 乔江, 卫佩佩. 一种用于中国地区的对流层天顶延迟实时修正模型[J]. 电子与信息学报, 2019, 41(1): 156–164 DU X Y, QIAO J, WEI P P. Real-time correction model for zenith tropospheric delay applied to the Chinese region[J]. Journal of Electronics & Information Technology, 2019, 41(1): 156–164. |
| [11] | NORDIUS A J. Estimation of tropospheric delay for microwaves from surface weather data[J]. Radio Science, 1987, 22(3): 379–386. |
| [12] | LANDSKRON D, BÖHM J. VMF3/GPT3: refined discrete and empirical troposphere mapping functions[J]. Journal of Geodesy, 2018, 92(4): 349–360. |


