2. 中国科学院大学, 北京 100049;
3. 昆明理工大学信息工程与自动化学院, 云南 昆明 650500
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Faculty of Information Engineering and Automation, Kunming University of Science and Technology, Kunming 650500, China
在射电干涉阵的成像研究中,随着观测视场的扩大,射电干涉阵成像时需要进行大视场成像。射电干涉阵的大视场成像方法包括三维傅里叶变换的方法[1-2],Faceting方法[3],W-projection方法[4]和W-stacking方法等[5-6]。
平方公里阵列(Square Kilometre Array, SKA)为射电干涉阵成像带来了新的挑战。平方公里阵列的巨大规模和复杂程度远远超出了现有射电天文望远镜阵列,全规模运行产生的海量数据需要10亿亿次/秒的处理能力,是2017年最快的超级计算机神威太湖之光处理能力(0.9亿亿次/秒)的10倍多[7]。因此,在射电干涉阵的数据处理中,多节点的并行化实现一直是研究的重要内容。
在射电干涉阵的成像中,大视场成像方法的并行实现已成为研究的重点。文[8]实现了W-projection的中央处理器(Central Processing Unit, CPU)并行和图形处理器(Graphics Processing Unit, GPU)并行,并在天河二号(MilkyWay-2)超级计算机上进行了实验,比较了单精度和双精度情况下数据加载时间和网格化运行时间。文[9]对uv域的Faceting成像方法并行化进行了研究。文[10]在uv域的Faceting成像方法和W-projection成像方法的基础上提出了一种新的方法w-facets,并通过多核中央处理器和图形处理器进行了并行实现。文[11]提出新的网格化核函数,并通过并行实现测试核函数在网格化时的性能。文[12]对提出的网格化方法进行了并行测试,给出了Strong Scaling下测试结果。
本文主要基于RASCIL对W-projection和W-stacking方法利用DASK进行中央处理器并行实现,分析在RASCIL中两种成像方法并行时的策略选择,以及并行资源的消耗,为后续基于RASCIL的射电干涉阵数据处理提供参考。
1 W-projection和W-stacking的实现框架W-projection和W-stacking是射电干涉阵大视场成像的经典算法,W-projection是CASA(https://casadocs.readthedocs.io/en/stable/)处理大视场成像的方法之一,而W-stacking是WSClean (https://gitlab.com/aroffringa/wsclean/)处理大视场成像的方法之一。
图 1是W-projection成像方法实现的原理框图,图中最左侧是射电干涉阵接收的可见度数据集,在成像前可见度数据集已完成校准,数据集加载后,可以获得观测的(u, v, w)分布,利用这些信息通过
| $ \begin{aligned} w_{\text {step }} & =\frac{\sqrt{2 \delta_{\mathrm{A}}}}{\pi F O V^2}, \\ N_w & =\operatorname{int}\left(\frac{1.1 \times 2.0 \times w_{\max }}{w_{\text {step }}}\right) \end{aligned} $ | (1) |

|
| 图 1 W-projection实现的原理框图 Fig. 1 Principles of W-projection implementation |
计算得到成像时所需要的w平面数Nw,其中,δA=0.02[9];FOV为成像的视场;wstep为相邻w平面的间隔;wmax为w的最大值。然后利用卷积核函数生成Nw个卷积核,这也是W-projection成像方法的关键,具有不同w的可见度数据与对应的卷积核进行卷积,实现从(u, v, w)向(u, v)平面的投影,卷积完成的可见度数据分布在(u, v)平面,并且进行叠加,最后通过傅里叶逆变换得到成像的脏图。
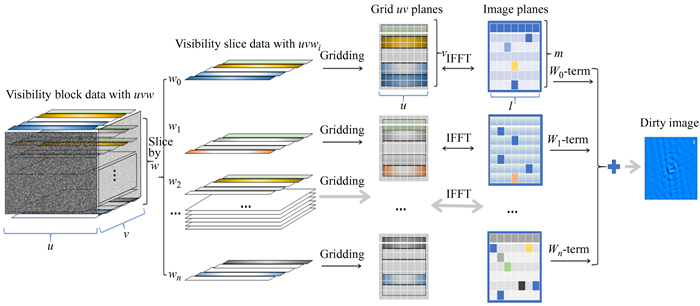
图 2是W-stacking成像方法实现的原理框图,图中最左侧是射电干涉阵接收的可见度数据集,同样该数据集已完成校准。数据集加载后,与W-projection相似,从(u, v, w)的分布通过(1)式计算需要的w平面数Nw,把可见度数据集按照不同的w值分为Nw个数据切片,每个数据切片与卷积核进行卷积网格化,这个卷积核分布在(u, v)平面。卷积网格化后每一个数据切片通过傅里叶逆变换得到该数据切片对应的图像,每一幅图像需要乘以
|
| 图 2 W-stacking实现的原理框图 Fig. 2 Principles of W-stacking implementation |
我们通过分析两种成像方法的实现框图发现,W-Projectin方法与W-stacking方法相同之处是都需要根据观测校准的可见度数据(u, v, w)的信息计算w平面数Nw。两种成像方法不同之处是W-projection方法需要根据w平面数计算投影的卷积核,卷积核数量与Nw一致,在计算时需要考虑卷积核的宽度和过采样点的数量,这两个因素影响卷积核的计算时间和占用空间;而W-stacking需要根据w平面数对可见度数据进行划分,将对应w值的可见度数据划分到同一个数据切片,数据切片集合的数量与w平面数Nw一致。W-stacking在卷积网格化环节中只需要一个卷积核,也就是所有数据切片会与同样的卷积核进行卷积网格化,网格化后再通过傅里叶逆变换得到数据切片对应的图像。
在成像处理过程中,W-projection需要计算与Nw数量相等的卷积核,因此这一部分的计算消耗超过W-stacking,但是由于W-stacking方法需要首先将可见度数据集进行划分数据切片,所以当可见度数据的规模达到一定程度时,需要特别考虑这一操作的计算效率;又因为W-stacking在实现时需要存储与w平面数相等个数的数据切片,因此,当可见度数据集具有一定规模时,需要的内存规模远远超过W-projection。
2 并行实验 2.1 实验数据实验数据来自Karl G. Janskey Very Large Array阵列的D阵型观测校准数据SNR_G55_10s.calib.ms,观测目标是超新星遗迹G055.7+3.4,观测的相位中心为19: 21: 40,DEC为21.45.00,观测日期从2010-08-23-01: 07: 14.00(UTC)至2010-08-23-08: 14: 54.00(UTC),观测频段是L频段1~2 GHz,包含4个频谱窗口,每个频谱窗口有64个频道,每个频道2种极化方式,数据大小为1.4 G。根据观测阵列的u, v, w分布,计算最长基线和最大w值,再根据成像时每个像素大小为8″,图像每个方向包含1 280个像素,可以根据(1)式计算得到在上述成像参数下,改正w-term的影响所必需的w平面数为68。
2.2 并行计算(1) 并行环境
本文使用RASCIL进行成像。RASCIL是一个完全开源的射电干涉阵列数据处理包,已广泛用于平方公里阵列数据模拟和处理研究,处理结果与其他软件进行比较后证实是可靠的。RASCIL用Python开发,在实验中使用的版本为v.0.1.9。
并行处理基于DASK进行,DASK也是一个开源库,为现有的Python堆栈提供并行性,DASK与Python库集成。在科学计算中数据集和计算规模的扩展速度远远高于处理器和内存发展的速度,科学计算往往需要扩展到多台计算机进行,DASK提供了可以跨多个核心、处理器和计算机实现并行执行。
(2) 实验硬件配置
成像实验使用相同配置的硬件作为计算节点,硬件配置如表 1。各个节点通过光纤万兆交换机和路由器进行连接组成以太网,保证各计算节点在同一局域网组网,每个节点有相同的网络延迟和带宽。
| Hardware | Model | Specification | Quantity |
| Motherboard | Intel(R) | C610 | 1 |
| CPU | Intel(R) Xeon(R) E5-2650L v4 | 14 cores 1.7 GHz 14 nm TDP65w | 2 |
| RAM | Samsung DDR4 | DDR4 2400 CRC | 192 GB |
| Hard disk | Samsung SSD 960 EVO | 512 GB | 2 |
| Network adapter | Intel X540-AT2 | 10 G Ethernet | 1 |
(3) 实验软件配置
操作系统为Ubuntu 22.04 LTS,开发语言环境为Python v3.8.2,并行计算框架为DASK2022.6.1,应用软件为RASCIL v0.1.9。
2.3 两种成像方法的并行策略两种大视场成像方法的并行实现中,当处理器负载最大,或者数据流带宽达到上限时,计算系统的吞吐量达到上限饱和,计算系统遇到瓶颈,无法提高处理速度。因此,成像算法并行化设计的前提是在保证计算系统吞吐量最大时对计算性能结果进行分析,即在不同算法和数据切片并行调度方式下,所分配的处理器资源或者带宽资源应接近100%占用率。
两种大视场成像算法的实现核心可以分为3部分:(1)数据集加载和数据集预处理;(2)计算任务和数据的分布式调度执行;(3)计算结果聚合,为下一环节管线做准备。
2.3.1 W-projection的并行策略W-projection能够分解成一些完全独立的子任务,同时各个子任务之间的数据几乎没有依赖,没有通信。以每通道可见度数据分配并行计算任务,数据由vis_load_ms task读入,创建各通道图像和卷积核(create_wp_gcfcf_from_vis),完成网格化相关invert和sum_invert task计算,并将各通道图像通过gather_image将图像结果汇集,如图 3,在图中需要持久化的计算环节用“P”标注。

|
| 图 3 W-projection的并行策略 Fig. 3 Parallel computing implementation of W-projection |
W-stacking以每通道可见度数据并行分配计算任务的方式,数据由load_ms task读入,每个通道做数据w_slice切片后进行Scatter-Gather并行执行,分片(Scatter)之后每个分片进行gridding_invert task计算,计算结果进行聚合(Gather),并将各通道图像结果汇集gather_image。W-stacking按照w进行数据分片,有两种并行策略:
(1) 多通道并行,每通道分片并行计算,这样会消耗非常多的内存资源,任务并行关系如图 4(a),其中持久化的计算结果环节用“P”表示。由于RASCIL中数据分片数量和任务数量相等,导致在并行处理时系统内存开销过大,因此,在目前的硬件配置下,这种策略无法得到成功的计算结果。

|
| 图 4 W-stacking的并行策略 Fig. 4 Parallel computing implementation of W-stacking |
(2) 多通道并行,每通道顺序分片并行计算,节省内存资源,任务并行关系如图 4(b),其中持久化的计算结果环节用“P”表示,因此,在W-stacking的并行实现时选择这种策略。
在图 3和图 4给出了4条数据通道的任务图,在实验中可见度数据的通道数最高为64。
3 结果讨论在成像方法的DASK并行计算实验中,为减少进程切换损耗和并行调度复杂度,每个执行单元(worker)对应一个进程和线程,执行单元总数量不超过处理器逻辑核心数量,每个执行单元最大内存为12 GB。
在并行处理中最小参考基准是单一执行单元,单一物理核心,单一进程和线程,对于超线程架构和睿频技术的中央处理器核心,逻辑核心计算性能不等同于物理核心计算性能。因此,在并行计算时按照同一计算场景,同一节点上56逻辑核心和28物理核心计算时间(分别为208.49 s和190.94 s)进行如下换算:
物理核心等于
(1) 在数据处理与计算规模恒定的情况下,即这时处理的可见度数据均为64通道,对应不同计算集群和中央处理器核心数量(每个执行单元对应一个物理或逻辑核心)配置下,对两种成像方法并行计算完成的时间进行比较,如表 2和表 3,可以看出在增加节点或节点的中央处理器核心数量时,两种成像方法的计算时间都减少。
| Number of nodes in cluster | Number of visibility channels | Physical cores per node | Equivalent logic cores | Execution time |
| 1 | 64 | 1 | 2.69 | 1 174 |
| 1 | 64 | n/a | 1 | 3 158 |
| 1 | 64 | 14 | 28 | 208.49 |
| 1 | 64 | 28 | 56 | 190.94 |
| 2 | 64 | 8 | 43.06 | 145.363 |
| 2 | 64 | 14 | 75.36 | 122.657 |
| 2 | 64 | 56 | 112 | 98.87 |
| Number of nodes in cluster | Number of visibility channels | Physical cores per node | Equivalent logic cores | Execution time |
| 1 | 64 | 1 | 2.69 | 3 843 |
| 1 | 64 | n/a | 1 | 10 327 |
| 1 | 64 | 14 | 28 | 512.61 |
| 1 | 64 | 28 | 56 | 580.80 |
| 2 | 64 | 8 | 43.06 | 429.251 |
| 2 | 64 | 14 | 75.36 | 324.400 |
| 2 | 64 | 56 | 112 | 260.70 |
(2) 在集群节点数量恒定为2,中央处理器物理核心数量随着处理数据规模等比例增加的情况下,并行计算完成的时间如表 4,由表 4可以看到,当数据规模不断增加时,随着物理核心数的增加,计算时间也在增加。
| Number of visibility channels | Physical cores | W-projection execution time | W-stacking execution time |
| 1 | 1 | 12.617 | 54.984 |
| 2 | 2 | 21.647 | 60.139 |
| 4 | 4 | 20.306 | 63.185 |
| 8 | 8 | 35.238 | 69.301 |
| 16 | 16 | 37.992 | 94.277 |
| 28 | 28 | 61.054 | 134.960 |
| 36 | 36 | 88.371 | 191.821 |
| 48 | 48 | 105.620 | 266.238 |
在并行处理中,加速比定义为
| $ \begin{aligned} & S_p=\frac{T_{\mathrm{s}}}{T_p}, \\ & E_p=\frac{S_p}{p} \times 100 \%=\frac{T_s}{p T_p}, \end{aligned} $ | (2) |
其中,Sp为加速比;Ep为并行效率;Ts为最优顺序算法的单处理核心执行时间;Tp为使用p个处理器核心并行计算所花费的时间。
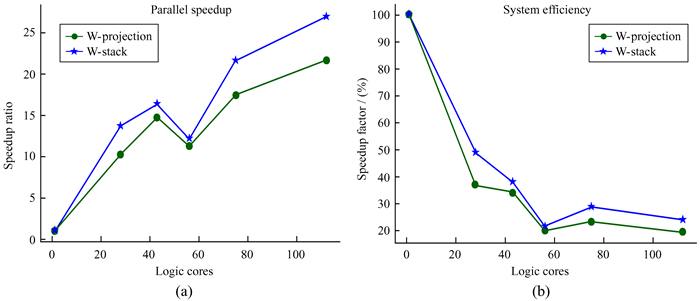
并行加速比和两种成像方法并行效率如图 5,其中(a)为两种成像方法的并行加速比,(b)为并行效率。由于并行任务的分配不一定和执行单元数量整除,计算时间和系统并行效率并不随运行中央处理器核心数量线性增加或减少,所以图中出现核心数多反而更慢的起伏点。处理密集运算时,并行效率衰减较快,这是因为一方面并行调度开销的增长,另一方面现代中央处理器睿频和超线程与多中央处理器的架构特性为少量核心运算的计算场景提供更好的核心性能。
|
| 图 5 并行加速比和并行效率 Fig. 5 Parallel speedup and system efficiency |
当处理的可见度数据规模发生变化时,针对两种并行计算资源配置的不同场景进行分析。
(1) Strong Scaling:并行处理时,问题规模保持不变(即可见度数据的通道数量不变),增加处理器数量,用于找到解决该问题最合适的处理器数量,即所用时间尽可能短又不产生太大的开销。两种成像方法在Strong Scaling资源配置模式的并行计算时间与加速比如图 6,(a)为W-projection,(b)为W-stacking。从图 6可以看出,在处理的可见度数据通道数量不变时,W-projection在43核心时达到计算速度与每核心使用效率的最佳平衡点,而W-stacking在28核时达到。

|
| 图 6 Strong Scaling资源配置 Fig. 6 Strong Scaling parallel computing configuration |
(2) Weak Scaling:并行处理问题规模随处理器数量增加而增加,适合这种并行资源配置策略时并行效率会保持水平稳定。测试结果如图 7,从图 7可以看出,并行效率迅速下降,因此, 两种成像方法的并行实现在数据规模发生变化时并不适合Weak Scaling并行资源配置策略。

|
| 图 7 Weak Scaling资源配置 Fig. 7 Weak Scaling parallel computing configuration |
本文首先介绍了W-projection和W-stacking两种大视场成像方法的实现原理,在此基础上完成基于RASCIL的W-projection和W-stacking方法的DASK并行实验,采用VLA-D阵列对超新星遗迹G055.7+3.4的校准观测数据集进行两种成像方法的并行处理,对两种成像方法设计了并行计算策略,在不同集群节点和处理器核心数配置下,分别在数据规模恒定和数据规模随处理器增长两种场景做了并行计算时间统计,对加速比和并行实现效率进行分析,并在数据规模增长时对比了两种成像方法在Strong Scaling和Weak Scaling两种策略下并行计算的优劣,两种成像方法适合采用Strong Scaling并行资源配置方式。由于在RASCIL v0.1.9版本中,可见度数据是利用visibility对象进行存储和访问的,在进行并行计算时该对象变得非常庞大,而W-stacking方法需要多次对visibility对象进行读写,所以该方法在并行计算时消耗的时间超过W-projection。在未来基于RASCIL的成像并行计算中,可以考虑对可见度数据采用更加简单的数据结构,这样能大幅提升W-stacking的成像效率。
| [1] | SRAMEK R A, SCHWAB F R. Imaging[C]//PERLEY R A, SCHWAB F R, BRIDLE A H. Synthesis imaging in radio astronomy. Astronomical Society of the Pacific Conference Series. 1989: 117-138. |
| [2] | CORNWELL T J, PERLEY R A. Radio-interferometric imaging of very large fields[J]. Astronomy & Astrophysics, 1992, 261: 353–364. |
| [3] | PERLEY R A. Wide field imaging Ⅱ: imaging with non-coplanar arrays[C]//PERLEY R A, SCHWAB F R, BRIDLE A H. Synthesis imaging in radio astronomy. Astronomical Society of the Pacific Conference Series. 1989: 259-276. |
| [4] | CORNWELL T J, GOLAP K, BHATNAGAR S. W projection: a new algorithm for wide field imaging with radio synthesis arrays[C]//Astronomical Society of the Pacific Conference Series. 2005: 86-90. |
| [5] | HUMPHREYS B, CORNWELL T J. Analysis of convolutional resampling algorithm performance[C]//Square Kilometre Array Memo. 2011: 1-13. |
| [6] | OFFRINGA A R, MCKINLEY B, HURLEY-WALKER N, et al. WSCLEAN: an implementation of a fast, generic wide-field imager for radio astronomy[J]. Monthly Notices of the Royal Astronomical Society, 2014, 444(1): 606–619. DOI: 10.1093/mnras/stu1368 |
| [7] |
戴伟, 汪森, 李秋虹, 等. 基于Spark的SKA1-MID自校准管线分布计算实现[J]. 天文研究与技术, 2020, 17(3): 334–340 DAI W, WANG S, LI Q H, et al. Implementation of SKA1-MID self-calibrating pipeline based on Spark[J]. Astronomical Research & Technology, 2020, 17(3): 334–340. |
| [8] |
劳保强, 安涛, 于昂, 等. uv-faceting成像并行算法研究[J]. 天文学报, 2019, 60(2): 25–40 LAO B Q, AN T, YU A, et al. Research on parallel algorithms for uv-faceting imaging[J]. Acta Astronomica Sinica, 2019, 60(2): 25–40. |
| [9] |
于昂, 劳保强, 王俊义, 等. 混合w-facets成像并行算法研究[J]. 天文学进展, 2020, 38(4): 421–435 YU A, LAO B Q, WANG J Y, et al. Research on parallel algorithms for hybrid w-facets imaging[J]. Prograss in Astronomy, 2020, 38(4): 421–435. |
| [10] | LAO B Q, AN T, YU A, et al. Parallel implementation of w-projection wide-field imaging[J]. Science Bulletin, 2019, 64(9): 586–594. DOI: 10.1016/j.scib.2019.04.004 |
| [11] | BARNETT A H, MAGLAND J, AF KLINTEBERG L. A parallel nonuniform fast fourier transform library based on an"exponential of semicircle" kernel[J]. SIAM Journal on Scientific Computing, 2019, 41(5): C479–C504. DOI: 10.1137/18M120885X |
| [12] | ARRAS P, REINECKE M, WESTERMANN R, et al. Efficient wide-field radio interferometry response[J]. Astronomy & Astrophysics, 2021, 646: A58. |


