2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
氢脉泽也称为氢频率标准,是一种利用氢原子固有特性提供精密时间频率参考的微波激射器[1]。氢脉泽优异的中长期频率稳定度使其长期在守时授时、导航定位、甚长基线干涉测量(Very Long Baseline Interferometry, VLBI)等系统中发挥着重要作用[2],其频率准确度、稳定性等各项指标深刻影响着众多关键设施的平稳运行[3-5]。氢原子在磁场中超精细能级结构分裂为F=1, mF=1; F=1, mF=0; F=1, mF=-1和F=0, mF=0共4个子能级,而氢脉泽就是基于F=1, mF=0和F=0, mF=0间的跃迁实现高稳定的频率输出[6]。根据Rabi-Breit公式以及gJ=2.002 256可以计算氢原子基态超精细能级的跃迁频率为[7]
| $ v_{0, 0}=v_0+2766 H_0^2, $ | (1) |
其中,H0为提供量子化轴的弱外磁场,由氢脉泽中的C场组件产生。显然空间不均匀的磁场H0会导致各部分原子共振频率不同,而实际的原子跃迁谱线是各部分原子谱线的叠加,在空间磁场不均匀的情况下,总的谱线宽度必然增加。不仅如此,原子在强度不同的磁场中运动时可能存在复合跃迁的频率成分,导致附加的受激跃迁,使原子能级寿命缩短,线宽增加[8]。由(1)式可以推得空间不均匀磁场导致的超精细能级跃迁频率相对变化率为[9]
| $ \frac{\delta f}{f_0}=5532 \frac{H_0^2}{f_0} \frac{\delta H}{H_0}, $ | (2) |
其中,f0=1.420 405 7 GHz;H0理论值为1 mGs,但实际上由于退磁等因素的影响,H0一般高于理论值。取H0=5 mGs,若使δf/f0 < 5 × 10-13,相应的磁场非均匀度δH/H0需要小于0.51%。
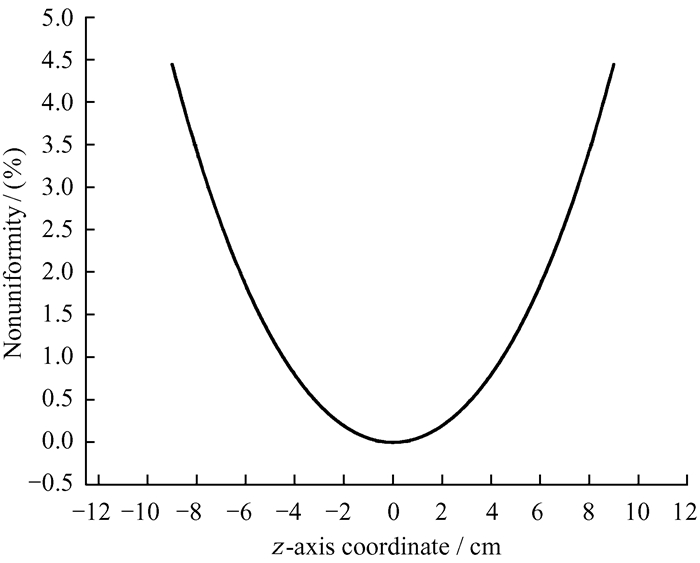
目前的空间主动型氢脉泽C场组件由一个单螺线管的主场筒和两个辅助线圈组成[10],中心螺线管与补偿线圈上的电流分别为0.386 mA和0.246 mA。利用仿真软件计算线圈中的磁场分布得到的非均匀度曲线如图 1。由图 1可知,该C场组件在储存泡区域的磁场最大非均匀度可达4.45%,对应的频率相对变化率高于4.33 × 10-12。而空间氢脉泽频率准确度的指标要求为5 × 10-13,显然带辅助线圈的单个螺线管产生的磁场不能满足氢脉泽C场的均匀度要求。文[11]提出利用3个相同半径的线圈增加磁场均匀性,文[12]证明并设计了9组线圈以内产生匀强磁场的方法,但线圈产生的磁场与螺线管产生的磁场并不相同,多组线圈叠加后匀强磁场的结果不能直接用于多段螺线管,需要重新计算。文[13]进行了九段线圈式C场组件研究,但其方法为利用仿真软件反复调整参数,研究过程繁琐,不具有普适性。相较于前人的工作,本文创新之处在于将高阶展式计算方法引入多段式螺线管的均匀度计算,并给出了高均匀度的不同宽度三段式螺线管的相应参数,之后利用有限元仿真计算了其磁场分布及非均匀度。四段及以上螺线管由于计算高阶展式系数时出现奇异矩阵,无法计算出相关参数,因此,本文采用线圈近似的计算方法,并给出了磁场分布的有限元仿真结果,计算了非均匀度分布。
|
| 图 1 带辅助场的单螺线管非均匀度分布 Fig. 1 Nonuniformity distribution of a single solenoid with auxiliary field |
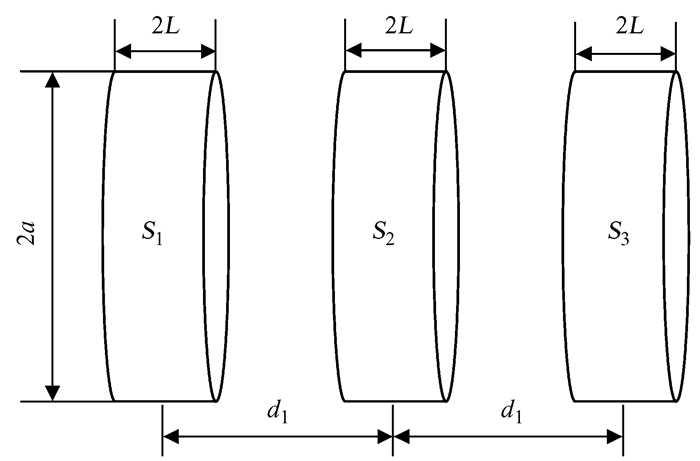
与线圈类似,虽然单个螺线管的磁场并不均匀,但可以通过在z轴叠加多个螺线管的方式产生磁场相对均匀的区域。理论上,螺线管段数越多,整体越接近于无限长螺线管,产生的磁场越均匀,但考虑到空间氢脉泽有限的容积,以及目前氢脉泽上的C场电流控制组件仅为三组,设计时首先考虑三段式螺线管。目前的C场螺线管加工工艺为印制电路板(PCB)上印刷导线,之后焊接为筒。由于不同宽度的螺线管在线路印刷以及焊接时的误差对磁场产生影响,采用三段相同宽度的螺线管为当前技术条件下的较优选择。图 2为所设计的三段螺线管式C场组件的结构示意图。
|
| 图 2 三段螺线管式C场组件示意图 Fig. 2 Schematic diagram of three-segment solenoid C-field |
对于三段螺线管,令每段螺线管的宽度和半径分别均为2L和a,螺线管S1和S3关于S2对称,与S2的距离都为d1。螺线管S2上的匝数与电流之积为ni,S1和S3上的匝数与电流之积为n1ni,n1为螺线管S1和S3的安匝比。单个螺线管内的轴向磁场分布为[14]
| $ B_z=\frac{a \mu n i}{2 \pi} \int_0^\pi\left[\frac{\xi(a-r \cos \theta) \mathrm{d} \theta)}{\lambda \sqrt{\xi^2+\lambda}}\right]_{\xi_{-}}^{\xi_{+}}, $ | (3) |
其中,λ=r2+a2-2arcosθ;ξ±=z±l;z和r为轴向和径向坐标;μ为真空磁导率。令r=0并积分即可得到轴向磁场在中心轴上的场强分布,
| $ B_{z, r=0}(z)=\frac{a \mu n i}{2}\left(\frac{z+L}{a \sqrt{a^2+(z+l)^2}}-\frac{z-L}{a \sqrt{a^2+(z-l)^2}}\right), $ | (4) |
因此,三段螺线管在中心轴上产生的复合磁场强度为
| $ B_c=B_{z, r=0}(z)+B_{z, r=0}\left(z+d_1\right)+B_{z, r=0}\left(z-d_1\right), $ | (5) |
在z=0处泰勒展开到四阶可得
| $ \begin{aligned} B_c= & B_c[0]+\frac{1}{2} B_c^{\prime \prime}[0] z^2+\frac{1}{24} B_c^{(4)}[0] z^4+O[z]^6 \\ = & \mu n i\left(\frac{l}{\sqrt{a^2+l^2}}+\frac{n_1\left(l-d_1\right)}{\sqrt{a^2+\left(d_1-l\right)^2}}+\frac{n_1\left(d_1+l\right)}{\sqrt{a^2+\left(d_1+l\right)^2}}\right)+\frac{3}{2} a^2 \mu n i\left(\frac{n_1\left(d_1-l\right)}{\left[a^2+\left(d_1-l\right)^2\right]^{5 / 2}}-\right. \\ & \left.\frac{l}{\left(a^2+l^2\right)^{5 / 2}}+O[z]^6-\frac{n_1\left(d_1+l\right)}{\left[a^2+\left(d_1+l\right)^2\right]^{5 / 2}}\right) z^2+\frac{5}{8} a^2 \mu n i\left(\frac{l\left(3 a^2-4 l^2\right)}{\left(a^2+l^2\right)^{9 / 2}}+\right. \\ & \left.\frac{-3 a^2+4\left(d_1-l\right)^2\left(d_1-l\right) n_1}{\left[a^2+\left(d_1-l\right)^2\right]^{9 / 2}}-\frac{-3 a^2+4\left(d_1+l\right)^2\left(d_1+l\right) n_1}{\left[a^2+\left(d_1+l\right)^2\right]^{9 / 2}}\right) z^4 . \end{aligned} $ | (6) |
仅有偶数阶是因为轴线上的磁场关于原点对称,即Bc为偶函数。显然,除了常数项其余高阶项为0的Bc为匀强磁场,因此令
| $ \left\{\begin{array}{l} \frac{1}{2} B_c^{\prime \prime}[0]=0 \\ \frac{1}{24} B_c^{(4)}[0]=0 \end{array}, \right. $ | (7) |
联立后即可解得n1和d1,归一化a, n, i后计算结果见表 1。
| L(a) | n1(a) | d1(a) |
| 0.05 | 1.874 47 | 0.763 |
| 0.1 | 1.853 23 | 0.772 |
| 0.15 | 1.818 31 | 0.787 4 |
| 0.2 | 1.77 | 0.809 |
| 0.25 | 1.716 67 | 0.838 26 |
| 0.3 | 1.643 8 | 0.874 7 |
| 0.35 | 1.570 3 | 0.919 15 |
| 0.4 | 1.495 06 | 0.971 93 |
| 0.45 | 1.422 25 | 1.033 |
| 0.5 | 1.355 36 | 1.101 9 |
由表 1可知,随着螺线管宽度2L增加,螺线管间的距离d1逐渐增大,而螺线管S1和S3的安匝比n1随之减小。由于氢脉泽内部的体积限制以及设计要求,C场筒总的高度与直径之比应当在1~1.5之间,对应于1≤L + d1≤1.5,因此只能选择0.2≤L≤0.4的三段螺线筒。
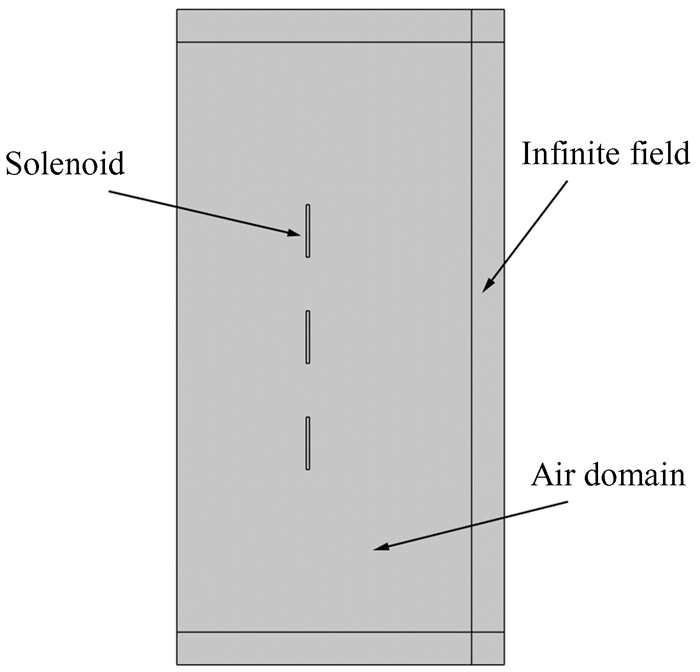
由于螺线管的轴向磁场和径向磁场的解析表达式都为积分形式,如果精确求解需要积分至无限远处,积分结果较为复杂,而利用有限元仿真软件可以较为便捷地计算三段式螺线管的空间磁场强度分布,进一步验证不同宽度的三段螺旋管产生磁场的均匀程度,并给出非均匀度分布。三段式螺线管产生的磁场呈轴对称分布,因此建模及剖分网格时采用轴对称结构。图 3为三段式螺线管的仿真建模,建模由螺线管、空气域以及无限元域三部分组成,引入无限元域是为了减小计算结果对空气域的影响,比起有限大的空气域更接近真实的物理环境,计算出的磁场分布也更加符合实际。螺线管区域位于r=20 cm处,宽度为0.5 cm,长度为12L cm。总的场强计算区域为50 cm × 100 cm的矩形,其中无限元域位于右侧、顶面及底面高度为5 cm的层。剖分网格后总的计算单元数为8 411,最大单元为0.4 cm,最小单元为0.002 cm,其中无限元域的单元数为5,单元大小比为1,增长公式为接近无限大的等差数列。为了方便结果的比较与分析,我们设置三组螺旋管线圈匝数均为20匝,切面的螺线管S2的单匝电流通量为1A,螺线管S1和S3的单匝电流通量为n1A,对应不同的安匝比。
|
| 图 3 三段螺线管磁场仿真建模 Fig. 3 Three-segment solenoid magnetic field simulation modeling |
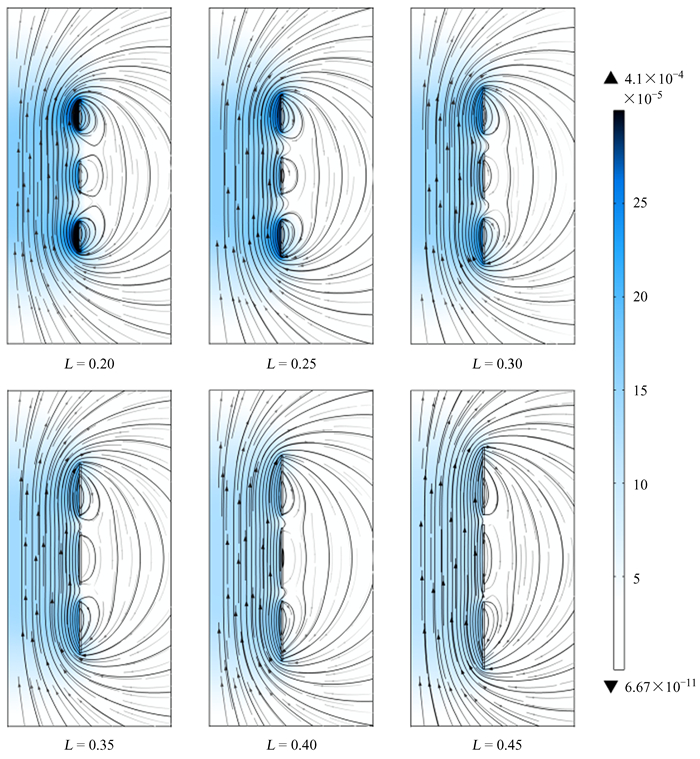
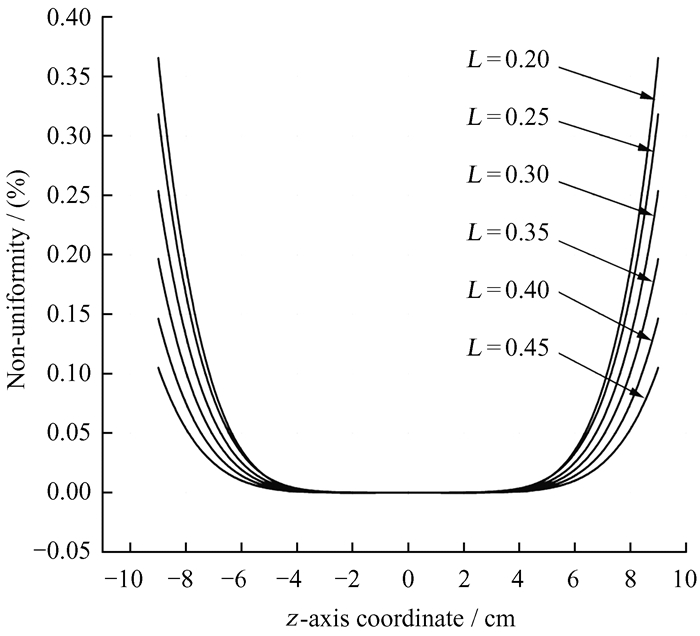
图 4为计算所得的不同宽度的三组螺线管产生磁场的空间分布以及磁力线。带箭头的黑色实线为磁力线,颜色深浅表示磁场强弱。由图中蓝色的深浅程度可知,三段螺线管中的磁场都较为均匀,在每段螺旋管匝数相同以及中心螺线管电流也相同的情况下,L越大,螺线管中的磁场越弱,越有利于降低跃迁频率的相对变化率。六组螺线管中的磁力线均较为平直,证明磁场的径向分量较小,可以有效减小由于磁场方向变换导致的频移。计算不同L的三段螺线管在轴线上的场强并绘制储存泡区域的非均匀度[H(z)-H(0)]/H(0)可得图 5。由图 5可知,随着L增大,储存泡区域的非均匀度最大值逐渐降低。对于L=0.45的三段线圈,最大非均匀度为0.105%,是带辅助线圈的单螺线管非均匀度的1/42。理论上可将跃迁频率相对变化率降低到原来的1/42,达到1.02 × 10-13。脉泽整体的频率准确度还取决于泡壁频移、二阶多普勒频移、腔牵引频移以及自旋交换频移等多种因素[15],三段螺线管式C场组件对脉泽的频率准确度的提高还需要进一步实测。
|
| 图 4 不同宽度的三段螺线管磁场分布 Fig. 4 Magnetic field distribution of three-segment solenoids with different widths |
|
| 图 5 不同宽度的三段螺线管磁场非均匀度分布 Fig. 5 Magnetic field non-uniformity distribution of three-segment solenoids with different widths |
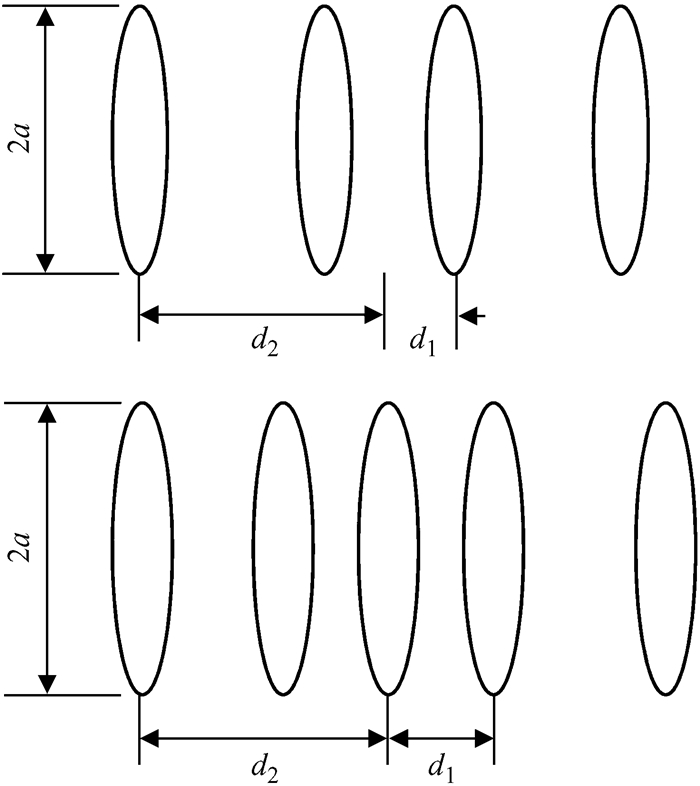
对于本文提出的多段螺线管构建匀强磁场的参数解法,理论上可扩展至三段以上螺线管,但在实际工作中,由于四段及以上螺线管的高阶泰勒展式过于复杂,利用软件数值求解的过程中产生奇异矩阵,无法生成有效的数值解。为此我们采用宽度与直径比小于0.04的螺线管,如图 6,此时可以将螺线管模型简化为线圈模型,求出四段及以上螺线管构建匀强磁场时的各项参数。
|
| 图 6 四组线圈及五组线圈示意图 Fig. 6 Schematic diagram of the structure of four sets of coils and five sets of coils |
单个n匝线圈的轴向磁场在r=0处的磁场强度为[12]
| $ B(z)=\frac{\mu n i a^2}{2\left(a^2+z^2\right)^{3 / 2}}, $ | (8) |
因此,四组线圈在z轴上产生的轴向磁场强度为
| $ \begin{aligned} B_{4 c}(z)= & \frac{\mu n i a^2}{2}\left(\frac{1}{\left[a^2+\left(d_1-z\right)^2\right]^{3 / 2}}+\frac{1}{\left[a^2+\left(d_1+z\right)^2\right]^{3 / 2}}+\right. \\ & \left.n_2\left(\frac{1}{\left[a^2+\left(d_2-z\right)^2\right]^{3 / 2}}+\frac{1}{\left[a^2+\left(d_2+z\right)^2\right]^{3 / 2}}\right)\right), \end{aligned} $ | (9) |
五组线圈在z轴上产生的轴向磁场强度为
| $ \begin{aligned} B_{5 c}= & \frac{\mu \text { nia }^2}{2}\left(\frac{1}{\left(a^2+z^2\right)^{3 / 2}}+n_1\left(\frac{1}{\left[a^2+\left(d_1-z\right)^2\right]^{3 / 2}}+\frac{1}{\left[a^2+\left(d_1+z\right)^2\right]^{3 / 2}}\right)+\right. \\ & \left.n_2\left(\frac{1}{\left[a^2+\left(d_2-z\right)^2\right]^{3 / 2}}+\frac{1}{\left[a^2+\left(d_2+z\right)^2\right]^{3 / 2}}\right)\right), \end{aligned} $ | (10) |
其中,n1和n2为安匝比;d1和d2为线圈间隔;μ为真空磁导率;a为线圈半径;n为线圈匝数。与三段螺线管相同,无论是四组线圈还是五组线圈,由于轴向磁场关于原点对称,其泰勒展式仅有偶数次项。对于四组线圈,有d1, n2和d2 3个未知数,将轴向磁场B4c在z=0处展开到7阶,
| $ B_{4 c}=B_{4 c}[0]+\frac{1}{2} B_{4 c}^{\prime \prime}[0] z^2+\frac{1}{24} B_{4 c}^{(4)}[0] z^4+\frac{1}{720} B_{4 c}^{(6)}[0] z^6+O[z]^8, $ | (11) |
并令
| $ \left\{\begin{array}{l} \frac{1}{2} B_{4 c}^{\prime \prime}[0]=0 \\ \frac{1}{24} B_{4 c}^{(4)}[0]=0 \\ \frac{1}{720} B_{4 c}^{(6)}[0]=0 \end{array}\right., $ | (12) |
联立即可解得d1, n2和d2。归一化a, n和i后计算得到d1=0.243 2, n2=2.260 4, d2=0.940 7。而对于五组线圈,有n1, n2, d1和d2 4个未知数,因此将轴向磁场B5c在z=0处展开到9阶,
| $ \begin{aligned} B_{5 c}= & B_{5 c}[0]+\frac{1}{2} B_{5 c}^{\prime \prime}[0] z^2+\frac{1}{24} B_{5 c}^{(4)}[0] z^4+\frac{1}{720} B_{5 c}^{(6)}[0] z^6+ \\ & \frac{1}{40320} B_{5 c}^{(8)}[0] z^8+O[z]^{10}, \end{aligned} $ | (13) |
令
| $ \left\{\begin{array}{l} \frac{1}{2} B_{5 c}^{\prime \prime}[0]=0 \\ \frac{1}{24} B_{5 c}^{(4)}[0]=0 \\ \frac{1}{720} B_{5 c}^{(6)}[0]=0 \\ \frac{1}{40320} B_{5 c}{ }^{(8)}[0]=0 \end{array}, \right. $ | (14) |
联立并归一化a, n和i后,计算得到n1=1.223, d1=0.409 2, n2=3.000 7, d2=1.080 1。
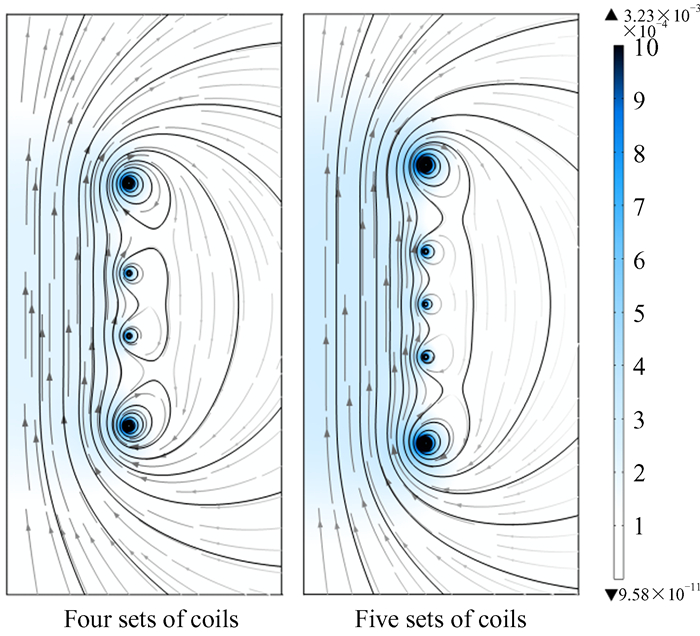
采用与第1部分相同的建模形式对四组及五组线圈进行磁场的有限元分析,仿真时每组线圈的匝数为20匝,宽度与半径分别为1 cm和20 cm,中心线圈上电流为1 A,其余线圈上电流由安匝比计算得到。图 7为仿真分析的磁场分布,由图 7可知,五组线圈在匝数与中心线圈电流相同的情况下,产生的磁场强度高于四组线圈,不利于降低频率相对变化率。
|
| 图 7 四组线圈及五组线圈的磁场分布 Fig. 7 Magnetic field distribution of four sets of coils and five sets of coils |
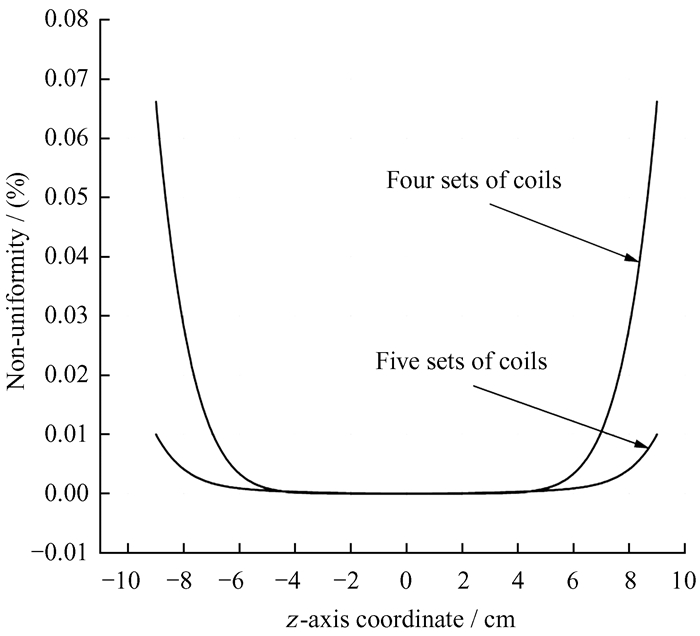
图 8给出了四组线圈和五组线圈在z轴储存泡区域的非均匀度分布。四组线圈在z轴的非均匀度最大值为0.066%,而五组线圈在z轴的非均匀度最大值为0.01%,显然五组线圈非均匀度优于四组线圈。理论上增加线圈组数可以进一步降低非均匀度,且各组线圈间的安匝比以及位置已由文[12]计算得出,但由于每组线圈需要相应的电流控制器,五组及以上线圈的C场组件设计将增加系统的复杂度,降低空间氢脉泽运行的可靠性。不仅如此,四组线圈对应的频率相对变化率为6.42 × 10-14,此时氢脉泽整体的频率准确度取决于泡壁频移以及二阶多普勒频移等因素,继续降低磁场不均匀所导致的频率相对变化可忽略不计,因此,四组线圈的设计已满足现有空间氢脉泽的均匀磁场要求。
|
| 图 8 四组线圈及五组线圈的非均匀度分布 Fig. 8 The non-uniformity distribution of four sets of coils and five sets of coils |
为降低氢脉泽由C场不均匀导致的跃迁频率相对变化率,本文提出了三段螺线管和四组线圈两种C场组件设计。经有限元仿真分析,L=0.45的三段螺线管式C场筒内磁场在储存泡区域的非均匀度最大值为0.105%,相应的跃迁频率相对变化率为1.02 × 10-13,而四组线圈式C场筒内磁场在储存泡区域的非均匀度最大值为0.066%,相应的跃迁频率相对变化率为6.42×10-14。目前C场组件为聚四氟乙烯薄板上刻等间距定位槽实现导线均布的螺线筒,加工工艺较为成熟,制作三段式螺线管只需在原有工艺的基础上缩减聚四氟乙烯板的高度即可。对于四组线圈式C场组件,由于所需的每组线圈宽度过窄,现有工艺无法实现,目前正在重新设计每组线圈的缠绕以及固定方式,之后将进行三段螺线管式C场组件与四组线圈式C场组件对氢脉泽输出频率、信号强度等指标影响的进一步比较研究。
| [1] | MAJOR F G. The quantum beat: principles and applications of atomic clocks[M]. New York: Springer, 2007. |
| [2] |
王玲玲. VLBI测站时频自动切换系统的设计和实现[J]. 天文研究与技术, 2015, 12(2): 166–173 WANG L L. Design and implementation of a time frequency system with auto-switching clocks at a VLBI station[J]. Astronomical Research & Technology, 2015, 12(2): 166–173. |
| [3] |
翟造成. 上海天文台研制的氢钟及其应用概况[J]. 中国科学院上海天文台年刊, 2001(1): 127–131 ZHAI Z C. Hydrogen clocks of Shanghai Astronomical Observatory and general situation of use[J]. Annals of Shanghai Observatory Academia Sinica, 2001(1): 127–131. |
| [4] |
翟造成. 我国氢钟研制现状与用于卫星导航的可行性[J]. 宇航计测技术, 2003, 23(5): 1–9 ZHAI Z C. The research status of domestic hydrogen masers and their application prospects for satellite positioning system[J]. Journal of Astronautic Metrology and Measurement, 2003, 23(5): 1–9. DOI: 10.3969/j.issn.1000-7202.2003.05.001 |
| [5] |
贯士俊, 翟造成. 上海天文台氢钟的研制现状及其应用前景[J]. 中国科学院上海天文台年刊, 2003(1): 136–142 GUAN S J, ZHAI Z C. The status of SHAO's hydrogen masers research and their potential application prospects in satellite navigation system[J]. Annals of Shanghai Observatory Academia Sinica, 2003(1): 136–142. |
| [6] | KLEPPNER D, BERG H C, CRAMPTON S, et al. Hydrogen-maser principles and techniques[J]. Physical Review, 1965, 138: A972–A983. DOI: 10.1103/PhysRev.138.A972 |
| [7] | HERTEL I V, SCHULZ C P. Atoms, molecules and optical physics[M]. Berlin: Springer, 2014. |
| [8] | VANIER J, TOMESCU C. The quantum physics of atomic frequency standards: recent developments[M]. New York: CRC Press, 2015. |
| [9] |
王义遒, 王庆吉, 傅济时, 等. 量子频标原理[M]. 北京: 科学出版社, 1986. WANG Y Q, WANG Q J, FU J S, et al. Physics of quantum frequency standards[M]. Beijing: Science Press, 1986. |
| [10] |
王文明. 一种应用于空间氢钟的C场组件设计[J]. 导航定位与授时, 2016, 3(1): 60–63 WANG W M. A design of C-field for space hydrogen maser[J]. Navigation Positioning and Timing, 2016, 3(1): 60–63. |
| [11] | WANG J, SHE S X, ZHANG S J. An improved Helmholtz coil and analysis of its magnetic field homogeneity[J]. Review of Scientific Instruments, 2002, 73: 2175–2179. DOI: 10.1063/1.1471352 |
| [12] |
胡朝晖, 穆维维, 吴文峰, 等. 产生匀强磁场的圆柱形线圈组设计方法[J]. 北京航空航天大学学报, 2018, 44(3): 454–461 HU Z H, MU W W, WU W F, et al. Design method of cylindrical coil systems for generating uniform magnetic field[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(3): 454–461. |
| [13] |
潘志兵, 谢勇辉, 帅涛, 等. 星载氢原子钟用多段线圈式C场的仿真及应用[J]. 天文研究与技术, 2020, 17(3): 341–348 PAN Z B, XIE Y H, SHUAI T, et al. Simulation and application of multi-section coil for C field used in space passive hydrogen maser[J]. Astronomical Research & Technology, 2020, 17(3): 341–348. |
| [14] | CALLAGHAN E E, MASLEN S H. The magnetic field of a finite solenoid[Z/OL]. (1960-10-01)[2022-05-26]. https://ntrs.nasa.gov/citations/19980227402. |
| [15] |
李玉莹, 翟造成. 氢原子钟壁移的测量和消除[J]. 波谱学杂志, 2011, 28(3): 378–382 LI Y Y, ZHAI Z C. Measurement and elimination of wall shift of hydrogen atomic clocks[J]. Chinese Journal of Magnetic Resonance, 2011, 28(3): 378–382. |


