2. 中国科学院射电天文重点实验室, 江苏 南京 210033;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Radio Astronomy, Chinese Academy of Sciences, Nanjing 210033, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
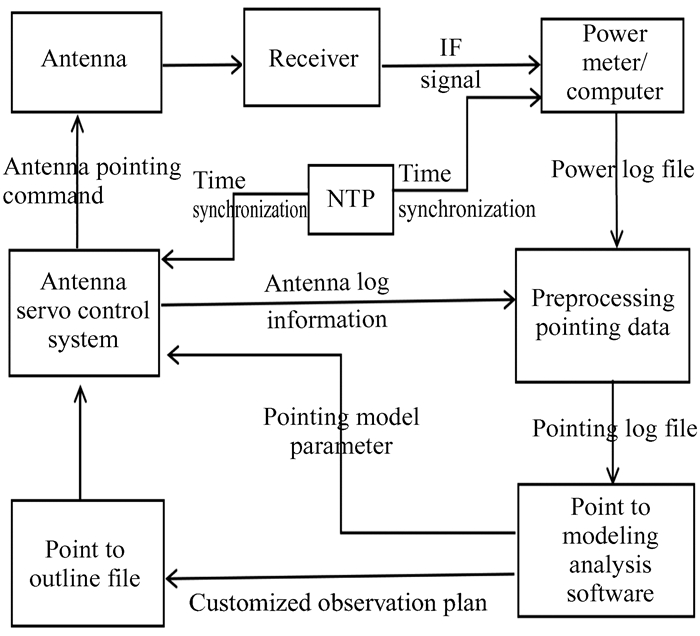
指向精度是射电望远镜的一个重要性能指标,指向好坏直接决定了望远镜能否接收到射电源信号,以及接收信号的信噪比。当天线指向偏离观测频率波束宽度的1/10时,天线效率损失约2.7%;偏离波束宽度的1/5时,天线效率损失约10.5%[1]。所以,一般对天线的指向要求是偏差小于1/10观测频率的波束宽度[2]。对于天马13 m射电望远镜,观测频率为15 GHz时,天线的指向偏差应小于30″。本文研究的指向建模结果远远优于这个指标。当前射电望远镜普遍采用指向模型校准天线的指向偏差:对全天区均匀分布的致密强射电源进行扫描观测,求出观测目标源的位置与理论计算的指向附近扫描获得的最大接收功率之间的偏差,利用天线指向模型修正公式,通过平差计算模型参数,然后将模型参数代入天线伺服控制系统,在天线跟踪射电源时,实时修正指向偏差。天线指向修正是一个迭代过程,尤其是新建的天线[3-4]。一般先扫描角径比较大的射电源修正比较大的误差项(编码器固有误差),然后对强的校准源进行观测扫描迭代模型验证,保证天线盲指精度满足观测要求。图 1为建立指向模型系统框图。在测试指向偏差时,根据目标源在天区的分布以及天线在该时刻对准目标源的方位俯仰角度定制指向纲要文件。天线伺服系统根据纲要文件对目标源进行扫描观测,同时记录天线的状态信息,分析观测数据,建立指向模型,将模型参数代入天线伺服控制系统。
|
| 图 1 建立指向模型系统框图 Fig. 1 The systematic diagram for building a pointing model |
常用检测和标定射电望远镜指向的方法为扫描河外射电源法和扫描人造卫星法。首先通过天文观测软件计算给定时间目标校准源的引导值(如地平式望远镜的方位角和俯仰角),控制射电望远镜在目标源理论指向位置附近进行方位和俯仰方向扫描,对功率计接收的辐射强度进行高斯函数拟合,确定辐射强度最大处的天线指向,进而得到引导指向和实测指向之间的差值,用该差值修正指向误差。人造卫星法测量指向偏差时,信号的信噪比高,对于配备制冷接收机的天线很容易造成信号接收链路饱和,且天区覆盖差。因此,我们一般采用扫描河外射电源法实现射电望远镜指向在全天区的标定[5]。
典型的指向扫描方式为十字扫描。早期天线扫描的具体实施过程为(1)计算目标源当前时刻的方位角和俯仰角,并引导天线指向该位置(Az0, El0);(2)在方位角偏开一个角度α,引导天线方位角在Az0-α到Az0+α范围内扫描,俯仰角以同样的方式扫描。由于地球自转的影响,该扫描方式的误差很大。目前,天马13 m射电望远镜在做指向测试时,根据目标源的特点,软件设定单点扫描的时间和宽度。在发送引导指令时,软件实时计算目标源的位置。比如方位扫描射电源3C 144,一个单点扫描的宽度为0.8°,时间为60 s,天线控制计算机与天线伺服控制单元的通讯频率为0.5 s,即天线每隔0.5 s接收一次引导值驱动天线指向引导值。所以一个单点扫描驱动天线120次指向引导值。这120次引导值为发送指令时刻目标源的方位角或俯仰角加一个范围在-0.4至0.4、长度为120的等比数列中的第i个元素,i表示第i次发送引导值,在方位方向发送指令需要除以目标源俯仰角的余弦函数[6]。
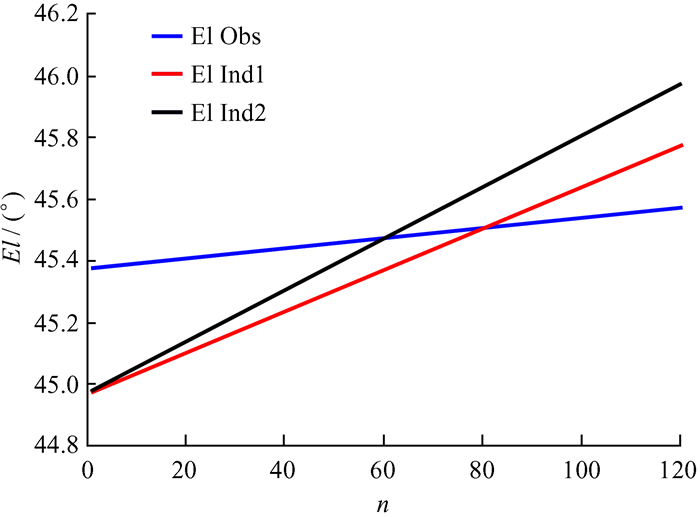
图 2为两种扫描策略中,天线指向目标源在一个单点扫描时天线俯仰角的实际值,假设天线系统没有延迟,且指向没有偏差,即引导值和实际值相等。图中横坐标为天线伺服控制单元发送指令的次数,纵坐标为天线俯仰角的实际值。其中“El Obs”表示在单点扫描过程中目标源的俯仰角变化;“El Ind1”表示上文所说的早期天线扫描时,一个单点扫描天线俯仰角的变化;“El Ind2”表示目前普遍采用十字扫描法,一个单点扫描天线俯仰角的变化。一次60 s的指向扫描,在第30 s时(指令发送的第60次)天线可以指向目标射电源。然而早期的扫描在第40 s时指向目标源,相当于台站控制系统与时间服务器相差10 s。显然这种指向扫描建模方式误差很大。
|
| 图 2 天线两种指向扫描方式的俯仰角变化 Fig. 2 Variation of the elevation of the antenna in two pointing scanning modes |
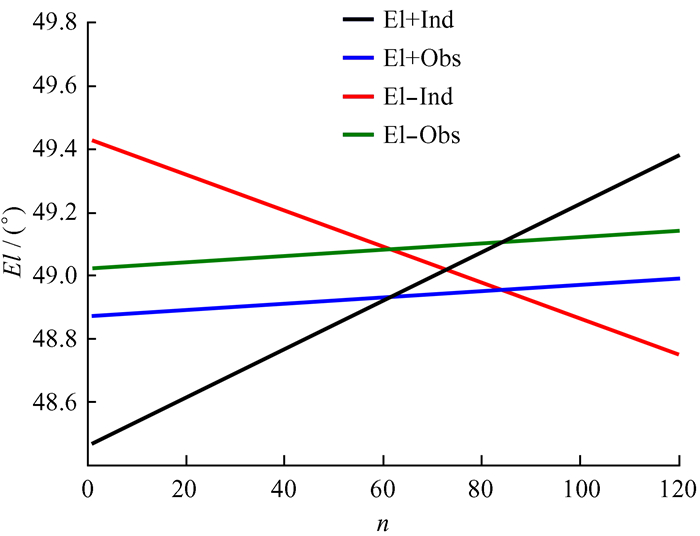
在实际天线控制过程中,天线引导值指令发送给ACU驱动天线转动。在这之间有系统延迟,且电机驱动天线转动也滞后。目前天马13 m射电望远镜指向建模采用引导天线分别以方位增加(Az+)、方位减少(Az-)、俯仰增加(El+)和俯仰减少(El-)共4个单点扫描作为对目标源的一次扫描,其中方位偏开扫描时俯仰实时跟踪,同理,俯仰偏开扫描时方位实时跟踪。台站日志文件记录扫描过程中的天线引导值、实际值和天线接收信号的测量功率值。图 3是天马13 m天线在指向扫描过程中俯仰角的运动轨迹。其中“El+Ind”表示天线El+扫描时天线俯仰角的实际值,“El+Obs”表示天线El+扫描时目标源俯仰角的值;“El-Ind”表示天线El-扫描时天线俯仰角的实际值,“El-Obs”表示天线El-扫描时目标源俯仰角的值。假设天线没有指向偏差,从天线的扫描轨迹分析误差的来源,在一次60 s的指向El+扫描过程中,在第30 s时(指令发送的第60次)天线俯仰应该指向目标源,然而实际轨迹显示俯仰角偏小,El-扫描时俯仰角偏大。采用同样的方式进行方位扫描时,Az+实际轨迹显示方位角偏小,Az-扫描时方位角偏大。这种误差是由于系统延迟造成的,所以在指向数据分析过程中,天马13 m射电望远镜指向一个位置的偏差是取正反扫描的平均值。后文指向数据分析的实测数据也验证了这个问题。
|
| 图 3 El+和El-指向扫描天线俯仰角转动范围 Fig. 3 The range of antenna elevation rotation for El+、El- pointing scan |
天马13 m射电望远镜在指向测量时,会记录扫描过程中天线方位角和俯仰角的引导值,以及当前时刻天线方位角和俯仰角的实际值和天线接收信号的功率值。经过数据分析,我们得到各个指向位置实际指向和引导指向的差值,并对全天区收集指向样本解算天线的指向模型,同时定标指向精度。
天线对河外射电源辐射的响应为天线方向图和射电源亮温分布的卷积,实时测量的功率值为该卷积在空间的采样。理想情况下,一个单点扫描的实测功率值为高斯分布。但是因为天线控制、采样、重力变形等不确定因素的影响,实际测量功率曲线存在附件噪声和扭曲,这对根据高斯拟合曲线的最大功率值求指向偏差带来测量误差。本文采用e指数函数叠加线性项进行功率数据拟合,原始数据采用
| $ p(x)=b_1 \exp \left[-0.5\left(\frac{x-b_2}{b_3}\right)^2\right]+b_4 x^3+b_5 x^2+b_6 x+b_7 $ | (1) |
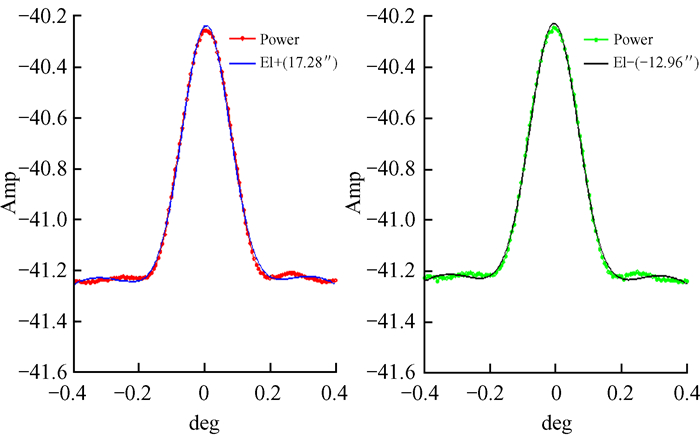
进行拟合。其中,p为测量的功率值;x为功率值的索引数;bi(i=1, 2, …, 7)为拟合参数。p的最大值对应的偏差,即天线指向的方位或俯仰偏差。图 4为天线俯仰扫描模式下功率曲线的拟合,横坐标表示天线俯仰引导值与实际值之差,纵坐标表示功率计读数。在俯仰扫描前,我们反复采用五点扫描法修正天线指向。实测数据分析表明,El+扫描的指向误差为17.28″,El-扫描的指向误差为-12.96″。这次扫描前指向进行了多次修正,这种结果是由天线控制系统的系统延迟和伺服系统响应滞后导致一个单点扫描(El+或El-)的测量误差造成的。因此,我们在一个指向点扫描时分别进行Az+,Az-,El+和El-共4次扫描,并分别取Az+和Az-,El+和El-的平均值作为方位和俯仰方向的指向偏差。
|
| 图 4 俯仰扫描模式下功率曲线的拟合 Fig. 4 Fittings of the power curve under elevation modes |
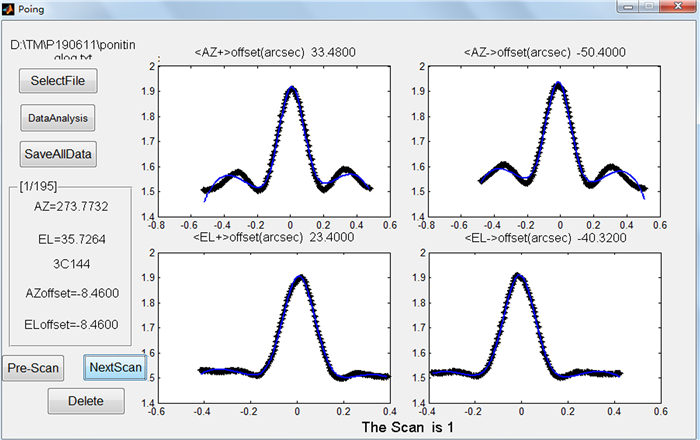
为了解算的指向模型精度高,需要指向样本点全天区覆盖面广且有足够的有效样本数。目前,天马13 m射电望远镜指向测量是将几个强的河外校准射电源添加到脚本库,循环交替扫描各个射电源,直到射电源的轨迹覆盖全天区。一次指向测量后,有大量的数据需要分析处理,为了方便每个单点扫描数据分析和模型参数拟合,我们开发了一套交互式数据分析软件,如图 5。
|
| 图 5 指向数据分析软件界面 Fig. 5 Software interface for point data analysis |
整个指向建模数据分析都可以由软件完成,首先点击“SelectFile”按钮选择要分析处理的数据文件;然后“DataAnalysis”分析文件中有多少个指向样本数(一个指向样本包括对一个源扫描的Az+,Az-,El+和El-),并记录文件中相应行的索引号;“NextScan”逐条分析对一个点的4次扫描偏差;“Pre-Scan”回放前一个样本的数据;“Delete”删除不好的指向样本数据;软件左边框显示每个指向样本数据的方位角、俯仰角、扫描的射电源、方位偏差和俯仰偏差;最后点击“SaveAllData”保存数据,“Model”输出模型参数文件。
4 指向修正模型拟合影响射电望远镜指向误差的原因是多方面的:整个天线各零部件的机械误差,天线系统的装配误差,射电望远镜受重力、温度变化、大气折射等因素。在射电望远镜指向误差源中,大部分具有重复性和规律性,我们可以通过相应的误差函数修正。对于固有的和具有变化规律的误差称为系统误差,该误差会导致天线在方位或俯仰方向产生指向偏差。传统指向模型是由
| $ \left\{\begin{array}{l} \Delta A z=p_1+p_3{\tan}El{\cos}Az+p_4{\tan}El{\sin}Az+p_5{\tan}El-p_6/{\cos}El \\ \Delta E l=p_2-p_3{\sin}El+p_4{\cos}Az+p_7{\cos}El+p_8/{\tan}El \end{array}\right. $ | (2) |
全天区拟合指向偏差ΔAz和ΔEl获得的八参数模型[7-8]。其中,p1为方位编码器固定零点偏差;p2为俯仰编码器固定零点偏差;p3和p4分别为天线方位轴和俯仰轴倾斜引起的误差项;p5为天线方位轴和俯仰轴不正交垂直导致的指向误差项;p6描述天线电轴和俯仰轴不正交引起的误差项;p7为天线重力变形因子;p8为残余大气折射误差。ΔAz和ΔEl分别表示天线每个指向的方位误差和俯仰误差。指向数据分析中统计天线方位指向误差用
| $ \delta_{A z}=\sqrt{\frac{\sum\limits_{i=1}^n\left(\Delta A z_i{\cos}E l_i\right)^2}{n}} $ | (3) |
计算方位角的均方根;俯仰指向误差用
| $ \delta_{E l}=\sqrt{\frac{\sum\limits_{i=1}^n\left(\Delta E l_i\right)^2}{n}} $ | (4) |
计算俯仰角的均方根;总体指向误差用
| $ \delta=\sqrt{\delta_{A z}^2+\delta_{E l}^2} $ | (5) |
计算天线指向误差的均方根。
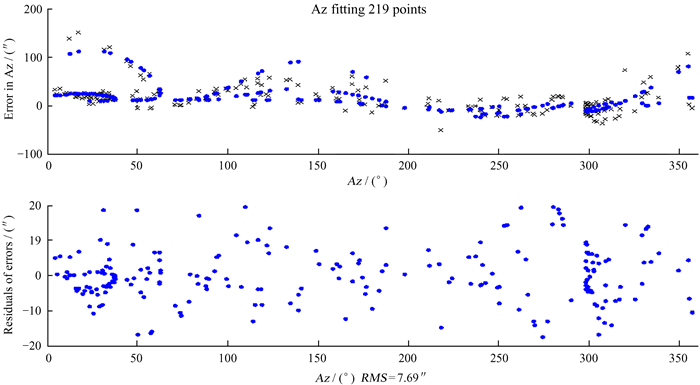
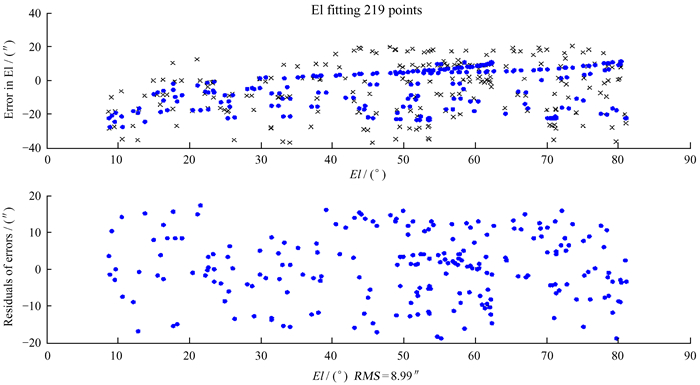
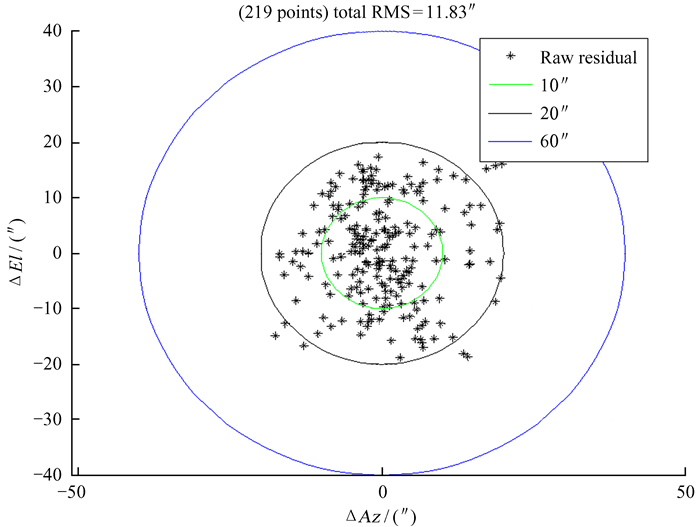
采用八参数模型对指向偏差测量采集的数据进行解析,得到拟合模型参数值。天线方位和俯仰拟合残差分布如图 6和图 7,从图中可以看出,指向样本数据分布均匀且覆盖天区范围广。经过模型拟合后指向在方位方向分布的残差为7.69″,在俯仰方向分布的残差为8.99″。天线指向在方位和俯仰方向整体残差分布如图 8,模型拟合后的残差为11.83″。图中“×”表示测量的指向样本数据,“·”表示模型拟合后的指向值。
|
| 图 6 指向数据方位拟合及残差分布 Fig. 6 Distribution of the point fitting errors and their residuals in the azimuth direction |
|
| 图 7 指向数据俯仰拟合及残差分布 Fig. 7 Distribution of the point fitting errors and their residuals in the elevation direction |
|
| 图 8 方位俯仰整体残差分布 Fig. 8 Distribution of the overall residuals in the azimuth and elevation directions |
建立指向模型后,把模型参数配置文件加载到天线伺服控制计算中,天线每次发送的引导值会加上模型偏差值。为了验证模型的准确性,对射电源进行指向扫描,计算出指向偏差,根据(3)~(5) 式计算得到方位方向的指向误差均方根为6.16″,俯仰方向的指向误差均方根为8.09″,总体指向误差为10.17″。
5 结论本文详细介绍了天马13 m射电望远镜指向修正建模的方法,分析对比了不同扫描方式对指向误差测量的影响,描述了处理观测数据的算法软件,最后建立了八参数指向模型,并将模型代入天线伺服控制系统,验证了模型的正确性,天线的盲指误差均方根可以达到10″。本文的研究可以为天线指向建模方法提供参考。
| [1] |
王锦清, 虞林峰, 赵融冰, 等. 大型射电望远镜高精度指向偏差检测方法[J]. 中国科学: 物理学力学天文学, 2017, 47(12): 129504 WANG J Q, YU L F, ZHAO R B, et al. High precision pointing error detection method for large radio telescope[J]. Scientia Sinica: Physica Mechanica & Astronomica, 2017, 47(12): 129504. |
| [2] |
马小辉, 孙中苗, 张志斌, 等. 利用射电天线轴线信息测定VLBI站点垂线偏差[J]. 测绘学报, 2021, 50(3): 315–323 MA X H, SUN Z M, ZHANG Z B, et al. Determining the deflection of the vertical of VLBI stations using radio telescope axis information[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(3): 315–323. |
| [3] |
温浩兴, 许谦, 王娜. 南山26米射电望远镜轨道高差测量及其对指向精度的影响[J]. 天文研究与技术, 2019, 16(2): 158–166 WEN H X, XU Q, WANG N. Measurement of NSRT 26 m antenna track unevenness and influence on pointing accuracy[J]. Astronomical Research & Technology, 2019, 16(2): 158–166. |
| [4] |
魏善祥, 王启明, 孔德庆, 等. 大型双反射面天线指向误差评估算法[J]. 天文研究与技术, 2020, 17(4): 513–521 WEI S X, WANG Q M, KONG D Q, et al. Algorithm for estimating pointing error of large dual-reflector antenna[J]. Astronomical Research & Technology, 2020, 17(4): 513–521. DOI: 10.3969/j.issn.1672-7673.2020.04.012 |
| [5] |
李金岭, 赵达新, 柳聪, 等. 佘山13 m口径射电望远镜指向扫描数据解析[J]. 武汉大学学报(信息科学版), 2020, 45(2): 159–166 LI J L, ZHAO D X, LIU C, et al. Analysis of pointing scan data of the Sheshan 13 m radio telescope[J]. Geomatics and Information Science of Wuhan University, 2020, 45(2): 159–166. |
| [6] |
虞林峰, 王锦清, 蒋甬斌, 等. 倾斜仪在提高TM 65 m射电望远镜指向精度上的应用[J]. 中国科学: 物理学力学天文学, 2019, 49: 129502 YU L F, WANG J Q, JIANG Y B, et al. Using inclinometer to improve the pointing accuracy of TM 65 m radio telescope[J]. Scientia Sinica: Physica Mechanica & Astronomica, 2019, 49: 129502. |
| [7] |
马小辉, 张志斌, 孙中苗, 等. 射电天线指向改正模型中轴系误差的完全表达式[J]. 天文学报, 2021, 62(1): 17–28 MA X H, ZHANG Z B, SUN Z M, et al. The complete expression of the axes related errors for the pointing calibration model of the radio telescope[J]. Acta Astronomica Sinica, 2021, 62(1): 17–28. |
| [8] |
虞林峰, 王锦清, 赵融冰, 等. TM 65 m射电望远镜指向模型的建立[J]. 天文学报, 2015, 56(2): 165–177 YU L F, WANG J Q, ZHAO R B, et al. Pointing model establishment of TM 65 m radio telescope[J]. Acta Astronomica Sinica, 2015, 56(2): 165–177. |


