2. 中国科学院大学, 北京 100049;
3. 中国科学院射电天文重点实验室, 江苏 南京 210033;
4. 国家天文科学数据中心, 北京 100101
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Key Laboratory of Radio Astronomy, Chinese Academy of Sciences, Nanjing 210033, China;
4. National Astronomical Data Center, Beijing 100101, China
射电天文学中,射频干扰定义为任何可能影响天文观测的有害信号。射电天文学发展过程中,抑制射频干扰一直是天文学家研究的热点。随着信息技术飞速发展,人为造成的干扰信号导致天文台站周围电磁环境恶化,影响射电望远镜正常观测。
射频干扰的来源多种多样,包括外部来源和内部来源。外部来源主要由天文台址外的设备产生,如人造卫星[1](北斗和全球定位系统导航卫星等)、飞机、台址附近的基站信号以及电视广播信号等;内部来源主要是天文台址内的电子设备,如计算机、视频监控、网络交换设备、无线输入设备等[2]。天文信号通常为宽频带且在时间尺度上平滑变化,而射频干扰在时域和频域的幅值强度高,绝大部分射频干扰与天文信号相比有明显差异[3]。射频干扰与热噪声不同,它通常由通信系统、人造雷达或电子设备产生的干扰构成,且具有复杂的时间和频率结构,常见通信信号的功率比天文信号高多个数量级并且随时间变化,因此无法通过长时间积分来降低强度,严重影响天文数据质量。天文学家针对上述问题已提出了多种射频干扰抑制方法,但仍受到以下因素制约:
(1) 随着无线技术的飞速发展及人类活动范围的扩大,地面及空间产生的人为干扰逐年递增。
(2) 随着制造技术和信息技术的飞速发展,射电望远镜向大口径或大规模阵列方向发展,随着多波束或相控阵馈源接收系统的投入使用,观测设备的灵敏度及数据收集能力显著提升,同时射频干扰抑制问题更加复杂。
在射电天文观测以及数据处理过程中需要针对不同阶段采取不同的射频干扰应对策略,本文将射频干扰抑制策略分为主动预防阶段、预相关阶段及后相关阶段,不同阶段的射频干扰问题可以采取不同的抑制方法。主动预防阶段若能采取有效防护手段,能够杜绝通信基站、电视广播等大部分射频干扰进入系统;预相关阶段采取参考天线及空间滤波等方法可以应对特定射频干扰源;后相关阶段可以采取阈值法处理幅值强度远大于天文信号的射频干扰,或利用机器学习相关技术实现射频干扰数据标记。下面针对不同阶段可采取的射频干扰抑制策略进行详细分析。
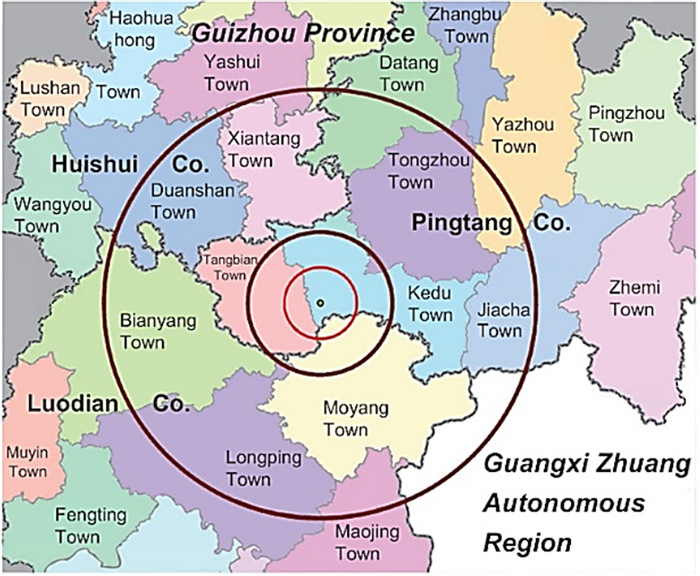
1 射频干扰主动预防阶段 1.1 电磁波宁静区射电望远镜观测来自宇宙遥远天体的微弱信号,对台址周边电磁干扰有较高要求,选择地理环境较好的台址及建立无线电宁静保护区是抑制射频干扰的重要一步,可以从根源上去除大部分干扰。500 m口径球面射电望远镜(Five-hundred-meter Aperture Spherical radio Telescope, FAST)是世界最大单口径、最灵敏的射电望远镜,位于贵州省黔南布依族苗族自治州平塘县克度镇大窝凼,以台址为中心,建立半径为30 km的电磁波宁静区,分为不同要求的3个区域。其中以台址为圆心,半径5 km范围为核心保护区,5~10 km的环带为中间区,10~30 km的环带为边远区[4],如图 1。电磁波宁静区能够屏蔽绝大部分外来干扰源。
新疆奇台110 m全向可动射电望远镜(Qi Tai Radio Telescope, QTT)[6]位于新疆昌吉州奇台县,以台址为中心,依据地形特征及当地实际情况, 规划了30 km的无线电宁静区。该宁静区共分为3个区域,分别为核心区、限制区和协调区,其中核心区为2.5 km×4 km的矩形区域;限制区为10 km×15 km的矩形区域[7-8],如图 2。
1.2 预留频段国际电信联盟(International Telecommunication Union, ITU)通过划分频谱来协调8.3 MHz~300 GHz之间的无线电频谱,将其分为几个频带,仅允许指定服务运行[9]。在分配的所有频段中,约有70到80个频段对应于射电天文学(确切的数量取决于地区和当地法律)。针对射电天文频段,一种是射电天文专用频段(或与无源服务共享),严格禁止无线电发射;另一种是与有源业务共享的频段,只能部分施加保护。射电天文的波段选择通常与科学目标有关。例如,氢线位于1 420 MHz附近,因此1 400~1 427 MHz频带给射电天文学保留[10]。
即使是射电天文专用频段,由于有源元件的谐波和功率泄漏,仍然可能存在干扰。对于这些情况,国际电信联盟在其ITU-R RA.769建议报告中将最大可接受的干扰定义为在测量功率中引入不超过10%的误差,这是天文学家普遍接受的阈值,该报告还为一些典型的天文波段提供了一份使用普通望远镜和观测参数的建议阈值清单[11]。
1.3 射频干扰主动预防策略的不足射频干扰主动预防策略中最直接的方法是为天文台选择远离干扰源的偏远位置。自然形态(例如山脉)可以有效阻止外部干扰,但干扰源会因为多径传播产生反射和衍射,从而增加干扰抑制的难度。研究发现,在望远镜台址周围种植松树等针叶树可以有效抑制射频干扰,针叶中的水分可以吸收1 GHz以上的信号[12]。部分天文台站建在高海拔地区以减少大气对观测的影响,远离人类活动范围,同时尽可能避免干扰源多径传播。面对内部干扰,通常的办法是在产生干扰的电子设备(计算机、微波和射频元件)上覆盖电磁屏蔽材料如导电箔,也可以将电子设备集中放入屏蔽室,将干扰控制在密闭空间,并不影响设备性能。
通常,主动预防是处理干扰的最有效方法,可以作为射频干扰的第1层防护。但仍然存在不足:
(1) 只能为电磁频谱的小部分提供保护;
(2) 对于高灵敏度的设备,电磁屏蔽材料不能完全屏蔽干扰;
(3) 卫星通信以及飞机等产生的干扰,由于相对位置限制,无法通过主动预防避免。
2 射频干扰预相关阶段本文将观测获取的原始数据在未写入磁盘形成可供科学研究处理之前的射频干扰处理阶段定义为预相关阶段。对于单天线观测可利用参考天线通过自适应滤波方式去除特定干扰,对于阵列天线可采用空间滤波方法抑制射频干扰。
2.1 自适应滤波自适应滤波算法是由Barnbaum和Bradley在1998年首次引入射电天文领域,用来解决射频干扰问题[13],在2005年,文[14]的现场试验证明,在射频干扰存在的情况下,自适应滤波方式能够极大提高脉冲星观测数据的质量。
参考天线接收的信号可以表示为
| $ R=R_{\text {noise }}+R_{\text {rfi }}+R_{\text {astr }} \text {, } $ | (1) |
其中,R为参考天线接收的信号;Rnoise为参考天线的系统噪声;Rrfi为参考天线接收的射频干扰;Rastr为参考天线接收的天文信号,天文信号通过参考天线的旁瓣接收,其强度微弱可忽略不计。同理,主望远镜接收的信号可以表示为
| $ M=M_{\text {noise }}+M_{\text {rfi }}+M_{\text {astr }}, $ | (2) |
主望远镜和参考天线接收的系统噪声不相关,而接收的射频干扰具有相关性。为了消除主天线中的射频干扰,使其对准射频干扰源,并通过不断优化参考天线的指向和极化方向提高参考天线中射频干扰的信噪比。
自适应滤波具体实现步骤:
(1) 在自适应相关环路中确定复增益系数g(该系数是不断迭代优化的)与参考天线接收的信号R相乘,逐步迭代gRrfi,使其大小接近主天线的射频干扰信号,能最大程度地消除主天线某一特定方向的射频干扰。
(2) 当g达到最优值时,gRrfi基本接近Mrfi,天文信号与参考信号的差值即去除特定干扰后的天文信号。
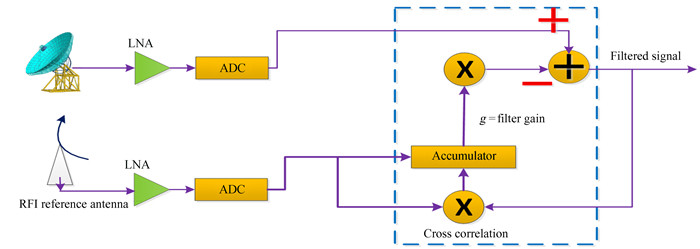
(3) 图 3为自适应滤波器基本设计图,将原始参考信号与滤波器输出相关,当相关系数为0时,达到最佳增益。
|
| 图 3 自适应滤波器基本设计图 Fig. 3 Adaptive filter basic design diagram |
相关项计算公式为
| $ C(g)=(M-g \cdot R) \cdot R, $ | (3) |
当C(g)=0时,可剔除主天线的射频干扰,即
| $ 0=M-g \cdot R \Rightarrow M=g \cdot R \Rightarrow g=\frac{M}{R} $ | (4) |
代入天线接收的各个分量得
| $ g=\frac{M_{\text {noise }}+M_{\text {rfi }}+M_{\text {astr }}}{R_{\text {noise }}+R_{\text {rfi }}+R_{\text {astr }}}=\frac{\left(M_{\text {noise }}+M_{\text {rfi }}+M_{\text {astr }}\right) \cdot\left(R_{\text {noise }}+R_{\text {rfi }}+R_{\text {astr }}\right)}{\left(R_{\text {noise }}+R_{\text {rfi }}+R_{\text {astr }}\right) \cdot\left(R_{\text {noise }}+R_{\text {rfi }}+R_{\text {astr }}\right)} . $ | (5) |
因为两个天线的系统噪声、天文信号、其他信号均与射频干扰不相关,参考天线中的天文信号非常微弱,可以忽略不计,即Rastr=0,那么上式进一步简化得
| $ g=\frac{M_{\mathrm{rfi}} \cdot R_{\mathrm{rfi}}}{R_{\mathrm{noise}}^2+R_{\mathrm{rfi}}^2} $ | (6) |
令Mrfi=ξRrfi,g可以写为
| $ g=\frac{\xi}{1+1 / R_{\mathrm{IN}}} $ | (7) |
其中,RIN是参考天线中的干扰噪声比(Interference-to-Noise Ratio, INR),等于Rrfi2/Rnoise2。我们可以明显看出,当干扰噪声比越大,g值越小,自适应滤波器效果越好。输出信号中射频干扰的残留量为
| $ \begin{aligned} S_{\mathrm{rfi}} & =M_{\mathrm{rfi}}-g \cdot R_{\mathrm{rfi}}=M_{\mathrm{rfi}}-\frac{\xi}{1+\frac{1}{R_{\mathrm{IN}}}} \cdot R_{\mathrm{rfi}} \\ & =\frac{M_{\mathrm{rfi}}+M_{\mathrm{rfi}} \cdot R_{\mathrm{IN}}-\xi R_{\mathrm{IN}} \cdot R_{\mathrm{rfi}}}{1+R_{\mathrm{IN}}}=\frac{M_{\mathrm{rfi}}+M_{\mathrm{rfi}} \cdot R_{\mathrm{IN}}-\frac{M_{\mathrm{rfi}}}{R_{\mathrm{rfi}}} \cdot R_{\mathrm{IN}} \cdot R_{\mathrm{rfi}}}{1+R_{\mathrm{IN}}}=\frac{M_{\mathrm{rfi}}}{1+R_{\mathrm{IN}}} . \end{aligned} $ | (8) |
在天文观测中,主天线指向待观测的天体,Mrfi在观测期间可以认为是恒定量,Srfi与干扰噪声比成反比,即干扰噪声比越大,Srfi越小,说明提高射频干扰在参考天线中的信噪比能提高主天线射频干扰抑制能力。
影响自适应滤波性能的几个因素:
(1) 混合射频干扰源
自适应滤波方法消除单源射频干扰效果较好,但是面对复杂的射频干扰环境,其抑制射频干扰的性能会大幅度下降。对于混合射频干扰,当两个干扰信号处于相同频域时,振幅大的干扰被消减。天文台址附近射频干扰来源复杂,且与天文信号相比具有较高的功率,在此类条件下自适应滤波方法射频干扰抑制效果一般[15]。
(2) 多路径传播影响
多径传播是指由于信号到达接收天线的路径不同,而存在同一信号多个副本的现象,通常是由大型陆地物体(山脉、建筑物)、大型水体(湖泊、泻湖)和电离层反射产生的。
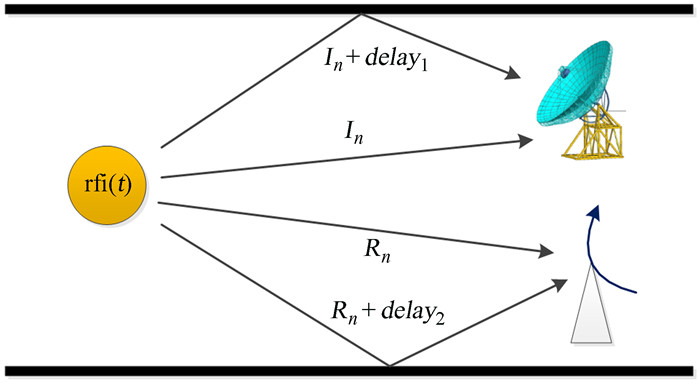
图 4为多路径干扰信号传播场景。因为到达望远镜和参考天线的多个副本有不同的时间延迟,如果延迟足够大,那么添加的信号就可以视为完全不相关。在这种情况下,多路径情况相当于多个射频干扰源,射频干扰信号种类繁多,难以获得滤波器多径传播的通用表达式。防止多径传播的最佳措施是将望远镜和参考天线放置在尽可能近的位置,以减小传播距离差异,并通过增加快速傅里叶变换点数来提高系统的频率分辨率,或在快速傅里叶变换点数不变的条件下减小系统带宽[15]。
|
| 图 4 射频干扰多径传播情况 Fig. 4 RFI multipath propagation situation |
(3) 违反线性时不变(LTI)条件
假设干扰传播路径至少在滤波器收敛的时间内满足线性时不变条件,如果不满足线性时不变条件,则表示射频干扰路径在某些地方呈现非线性或时变的传播特性。然而,没有任何自然介质表现出足够强的非线性,或具有快速变化的传播特性而影响滤波器的性能,特别是考虑到最终算法收敛时间是毫秒级的。当望远镜跟踪天体时,捕获射频干扰的旁瓣随望远镜一起移动,被测射频干扰的路径特性随时间逐渐变化。自适应滤波方法需要具备相应计算能力,不会因望远镜缓慢移动而受到明显影响。
接收机前端的一些模拟元件是信号饱和的,如放大器和频率混频器。当一个分量达到饱和时,输入信号的幅值会被削去,从而产生谐波失真,影响系统的线性时不变条件。这种失真被视为附加的损坏信号,其频率是原始输入信号中心频率的几倍。此外,由于数字化后的混叠等原因,谐波信号往往被混入基带,从而破坏天文数据。主信道射频干扰谐波失真会严重破坏滤波器性能,附加的谐波信号不会出现在参考信道中,使得这类射频干扰更难抑制[15]。
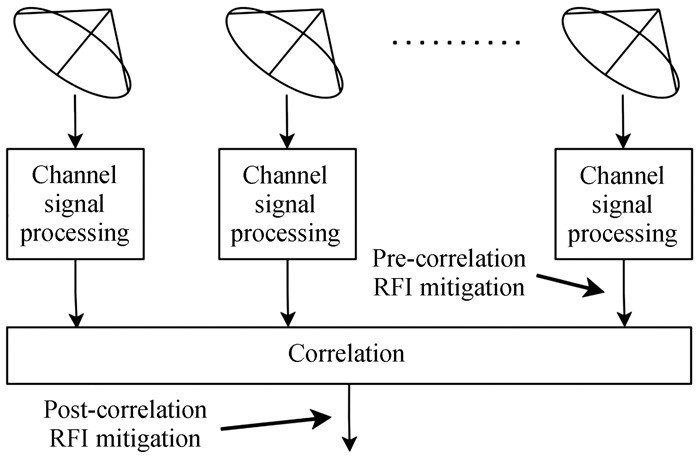
2.2 空间滤波空间滤波方法主要针对多通道射电天文观测中的射频干扰抑制问题[16-18],该技术适用于干涉射电望远镜阵列,如荷兰的Westerbork综合射电望远镜(Westerbork Synthesis Radio Telescope, WSRT)、美国的甚大阵列(Very Large Array, VLA),或配置了相控阵接收系统的单天线望远镜。图 5为空间滤波技术在天线阵列系统中的应用。
|
| 图 5 天线阵列系统在不同阶段抑制射频干扰 Fig. 5 Antenna array system suppresses RFI at different stages |
射电望远镜接收的信号由3部分组成,射电源信号(拟观测目标)、系统噪声和射频干扰。系统噪声由宇宙背景噪声、大气噪声、接收机噪声等噪声分量组成。根据中心极限定理,系统噪声是时间独立且高斯分布的信号,在短时间间隔上是短时平稳的,且所有的射电源假定在统计学上彼此独立[12]。
射电天文学中的射频干扰特征是各种各样的。本文选择中心窄带高斯平稳、二阶非周期和循环平稳信号3种不同的信号特性对射频干扰建模。
天线阵列共有M个天线,其中x(t)=[x1(t)…xM(t)]T表示M×1个天线阵列的输出,其中,第k个天线在t时刻的输出为xk(t),那么x(t)可以写为
| $ x(t)=A_c \cdot c(t)+A_r \cdot r(t)+n(t), $ | (9) |
其中,
通过协方差矩阵描述射电源在时间维度上的相关性,即
| $ R(t, \tau ) = E\left\{ {x\left( {t + \frac{\tau }{2}} \right) \cdot {x^{\rm{H}}}\left( {t - \frac{\mathit{\tau }}{2}} \right)} \right\}, $ | (10) |
其中,R(t, τ)为在t时刻τ范围内射电源信号的相关性;xH代表x的共轭转置。假设射频干扰、射电源和系统噪声三者相互独立,即互不相关,那么
| $ \begin{aligned} & E\left\{c_n\left(t+\frac{\tau}{2}\right) r_m^*\left(t-\frac{\tau}{2}\right)\right\}=0, \quad \forall \tau, n \in\left[1 \cdots N_c\right], m \in\left[1 \cdots N_r\right], \\ & E\left\{c_n\left(t+\frac{\tau}{2}\right) n_m^*\left(t-\frac{\tau}{2}\right)\right\}=0, \quad \forall \tau, n \in\left[1 \cdots N_c\right], m \in[1 \cdots M], \\ & E\left\{r_n\left(t+\frac{\tau}{2}\right) n_m^*\left(t-\frac{\tau}{2}\right)\right\}=0, \quad \forall \tau, n \in\left[1 \cdots N_r\right], m \in[1 \cdots M] . \end{aligned} $ | (11) |
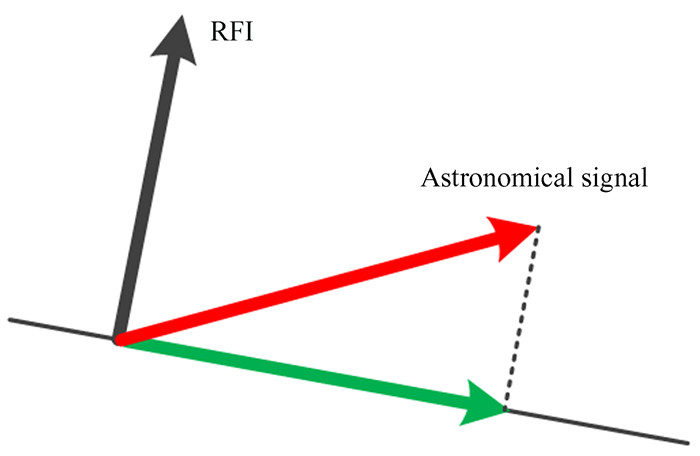
从线性代数的观点来看,相控天线阵列射电望远镜数据协方差矩阵可以看作是线性变换矩阵。这个矩阵生成一个数据向量空间,该向量空间由射频干扰子空间、射电源子空间和系统噪声子空间组成。图 6展示了一个无噪声场景下的二维数据向量空间的示例。红色和黑色矢量分别代表与射电源和射频干扰源相关的向量。
|
| 图 6 二维数据向量空间的正交投影 Fig. 6 Orthogonal projection of a two-dimensional data vector space |
使用正交投影技术减少干扰,将数据向量空间投影到与射频干扰子空间正交的子空间上,投影的射频干扰子空间完全为0,由此产生的数据只包含射电源。
从图 6可以清楚地看出,在投影后,恢复的射电源能量取决于两个向量的夹角大小,即
| $ P_{\text {proj }}^2=P^2 \sin \left(\theta_{a_c, a_{r_n}}\right), $ | (12) |
其中,P2为射电源的功率;θac, arn为射频干扰向量与射电源向量的夹角大小,在0~90°范围内,θac, arn越大,最终投影得到的射电源功率越大。但是射电源子空间和干扰子空间之间的夹角难以测量,需要借助投影矩阵间接计算。
设投影矩阵为P,它的特征值是0或1。特征值为0对应的特征向量生成投影核子空间,特征值为1对应的特征向量生成值域子空间。因此投影矩阵的秩等于它的值域子空间的维数。如果H是投影范围子空间基,K是投影核子空间基,则有
| $ \mathit{\boldsymbol{P}} \cdot \mathit{\boldsymbol{H}} = \mathit{\boldsymbol{H}}, \mathit{\boldsymbol{P}} \cdot \mathit{\boldsymbol{K}} = 0. $ | (13) |
由基矩阵H生成的投影矩阵定义为
| $ \boldsymbol{P}=\boldsymbol{H}\left(\boldsymbol{H}^{\mathrm{T}} \boldsymbol{H}\right)^{-1} \boldsymbol{H}^{\mathrm{T}}, $ | (14) |
其值域是正交于H的子空间的正交投影为P⊥,定义为
| $ \boldsymbol{P}^{\perp}=\boldsymbol{I}-\boldsymbol{H}\left(\boldsymbol{H}^{\mathrm{T}} \boldsymbol{H}\right)^{-1} \boldsymbol{H}^{\mathrm{T}}. $ | (15) |
在多干扰的情况下,干扰子空间是多维的,这个子空间是由存储在矩阵Ar中的独立射频干扰向量集合生成。因此,投影矩阵可以表示为
| $ \boldsymbol{P}_r^{\perp}=\boldsymbol{I}-\boldsymbol{A}_r\left(\boldsymbol{A}_r^{\mathrm{T}} \boldsymbol{A}_r\right)^{-1} \boldsymbol{A}_r^{\mathrm{T}}. $ | (16) |
在预相关阶段,可用数据为天线阵列输出数据向量x(t),将其投影到射频干扰子空间的正交空间,修正后的数据向量xclean(t)为
| $ \boldsymbol{x}_{\text {clean }}(\boldsymbol{t})=\boldsymbol{P}_r{ }^{\perp} \boldsymbol{x}(\boldsymbol{t}). $ | (17) |
从以上内容可知,空间滤波需要预先知道干扰源的来源,以便确定投影矩阵,对于复杂的干扰环境,测定干扰源的具体位置是非常困难的。
3 射频干扰后相关阶段由于射频干扰信号强度通常比天文信号大几个数量级,阈值法是一种有效抑制射频干扰的方法。阈值水平通常根据统计量决定,可以用一段数据的均值、均方根等作为阈值参考值,超出这个范围的值标记为射频干扰。阈值法不足之处是会误将天文信号标记为射频干扰,在后相关阶段降低射频干扰检测的错误率是研究射频干扰抑制问题的一个重要方向。
3.1 VarThreshold算法在频域和时域上,射频干扰往往影响相邻的数据,因为其强度比较低,不会被标记为射频干扰,增加了检测射频干扰的错误率。VarThreshold是一种组合阈值算法,其思想是当组合样本的某一统计属性超过某个限值时,将标记样本的组合为射频干扰[19-20]。假设A和B是相邻的样本采样点,常规阈值法是分别查看样本A和B是否超过设定的阈值水平线,如果超过,则标记为射频干扰。但对于组合阈值来说,只有样本A和B都超过阈值,才将这一组合的样本都标记为射频干扰。如果样本A和B没有被标记为射频干扰,它们将和下一个相邻的采样点C进行组合,继续与阈值进行对比,迭代多次完成射频干扰标记。算法公式为
| $ \mathit{flag}{\mathit{v}_M}(v, t) = \exists i \in \{ 0, \cdots , M - 1\} :\forall j \in \{ 0, \cdots , M - 1\} :|R(v + a\Delta v, t)| > {\chi _M}, $ | (18) |
(18) 式表达了从t时刻起,M个数的范围内,如果该范围内所有采样点的绝对值大于χM,那么将这M个数都标记为射频干扰。
VarThreshold算法用一组严格递减的阈值序列χi(i=1, …, N)判定某个采样点是否应被标记为射频干扰,公式为
| $ {\chi _i} = \frac{{{\chi _1}}}{{{\rho ^{{{\log }_2}i}}}}, $ | (19) |
其中,χ1是单采样点阈值,当ρ=1.5时效果最好。χ1的取值由数据的统计水平量决定,即选取的阈值使射频干扰的假阳率最小。
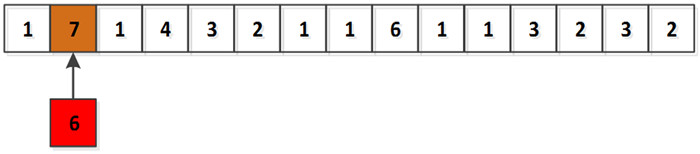
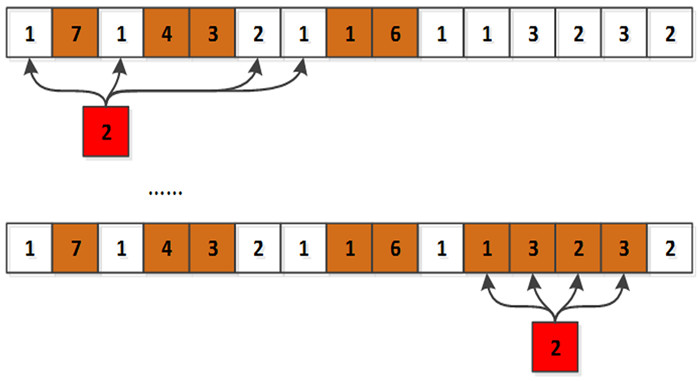
3.2 SumThreshold算法SumThreshold算法也是一种组合阈值算法[19-20],与VarThreshold算法求解阈值序列类似,只是ρ值不同,当ρ=1.2时效果最好。求出一组阈值T={T1, T2, T4, …},通过迭代的方式与样本进行比较,即T1与单样本比较,T2与两个样本的均值比较,Tm与m个样本的均值比较,当样本均值大于阈值时,标记为射频干扰,且不参与后续的迭代计算过程。以一维序列为例,设序列为{1, 7, 4, 3, 2, 1, 1, 6, 1, 1, 3, 2, 3, 2},阈值χ为{χ1=6, χ2=3, χ4=2}。
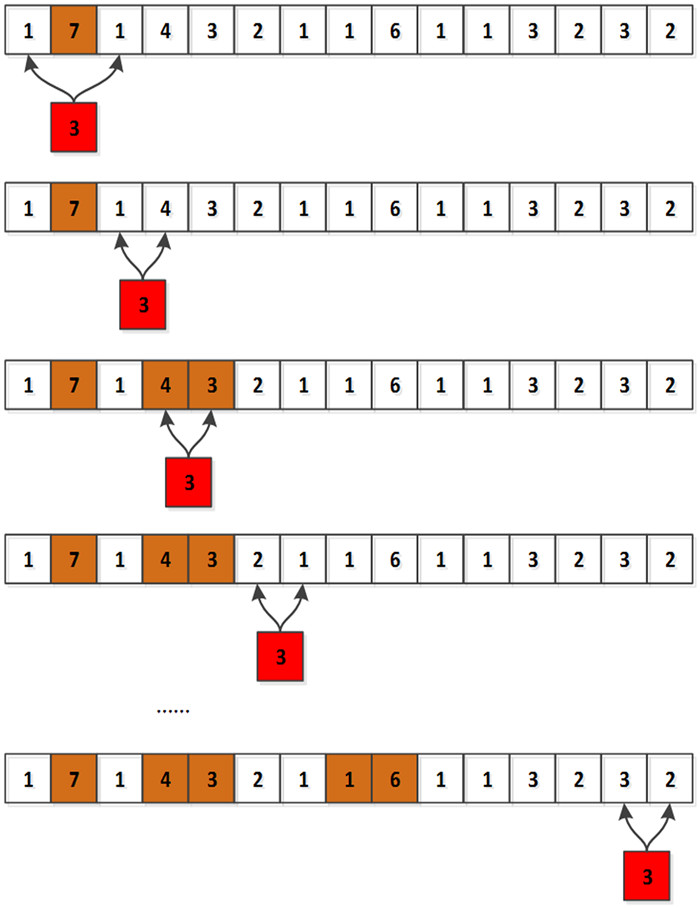
图 7、图 8和图 9展示了SumThreshold算法的过程。从算法角度考虑,该算法的时间复杂度为O(n2)。为了减小计算速度,当阈值M取1, 2, 4, 8, 16, 32, 64, 128, 256 …时,时间复杂度降至O(nlogn)。
|
| 图 7 第1轮,阈值为χ1=6,只有7被标记 Fig. 7 In the first round, the threshold is χ1=6 and only 7 is marked |
|
| 图 8 第2轮,阈值为χ2=3 Fig. 8 In the second round, the threshold value is χ2=3 |
|
| 图 9 第3轮,阈值为χ4=2 Fig. 9 In the third round, the threshold value is χ4=2 |
奇异值分解是线性代数中一种重要的矩阵分解,能够提取信息,简化数据,去除噪声等,可将数据映射到低维空间[21]。奇异值可以分解为
| $ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{U \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{V}}^{\rm{T}}}. $ | (20) |
如(20)式,奇异值分解将原始矩阵A分解为3个矩阵:U, Σ和VT,其中U和V是正交矩阵,Σ是对角矩阵,对角线上的元素为奇异值。绝大部分射频干扰信号在时域或频域上的振幅较大。用A代表接收的天文信号,将其进行奇异值分解,即
当射频干扰信号足够强,且σRFIσastro=0时,算法效果最好。该方法仅适用于宽带射频干扰信号,对于遵从高斯分布的射频干扰信号并不适用[19-20]。
4 基于机器学习的射频干扰抑制方法随着机器学习和深度学习等技术快速发展以及天文数据的急速增长,两者的结合已成必然趋势。通过对大量数据进行学习和训练后,能有效地标记天文信号中的射频干扰,并进行特征提取。
4.1 主成分分析法(Principal Component Analysis, PCA)主成分分析是一种用于数据特征降维的方法,常用于减少数据集的维数,同时保持数据集对方差贡献最大的特征。这样低阶成分往往能够保留数据的重要信息,方便特征提取和分类[22-23]。
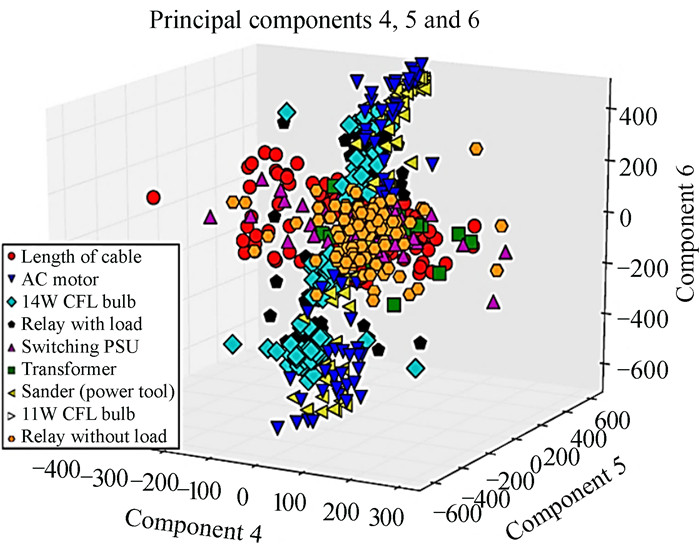
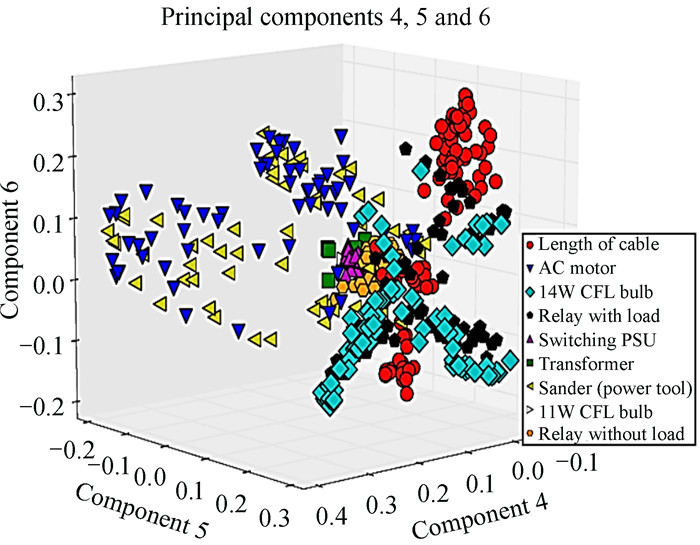
文[24]对生活中常见的9种瞬时射频干扰来源进行分类测试实验,在时域范围内分别使用标准主成分分析和核主成分分析进行测试。之后用聚类分离的方法比较了两种方法的聚类精度,结果如图 10和图 11,发现核主成分分析在区分来源方面比标准主成分分析更好,能有效区分瞬时射频干扰来源。
4.2 支持向量机(Support Vector Machine, SVM)在机器学习中,支持向量机是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法[25]。
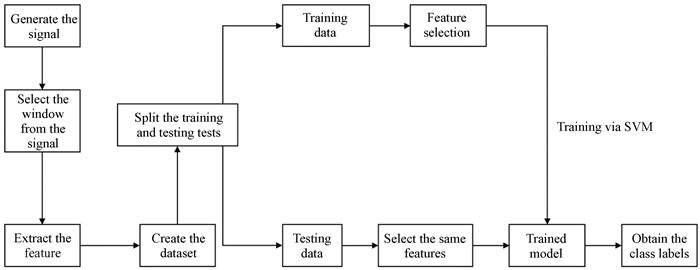
文[26]选取时间长度为300 μs的非射频干扰和射频干扰信号训练,提取均方根、均值、方差、均值与方差之比、偏度、峰度、最大振幅、最小振幅和峰值个数等信息,导入支持向量机训练模型,之后对测试数据进行射频干扰和非射频干扰分类,流程如图 12。结果表明,即使干扰噪声比低和射频干扰占空比小的情况下,该方法仍能准确地检出射频干扰,效果良好。
|
| 图 12 基于支持向量机的射频干扰抑制过程 Fig. 12 RFI suppression process based on SVM |
神经网络的基本结构包含输入层、隐藏层和输出层,由大量节点相互连接构成,是一种非线性统计数据建模工具,常用来对输入和输出间复杂的关系进行建模,或用来探索数据的模式[27]。
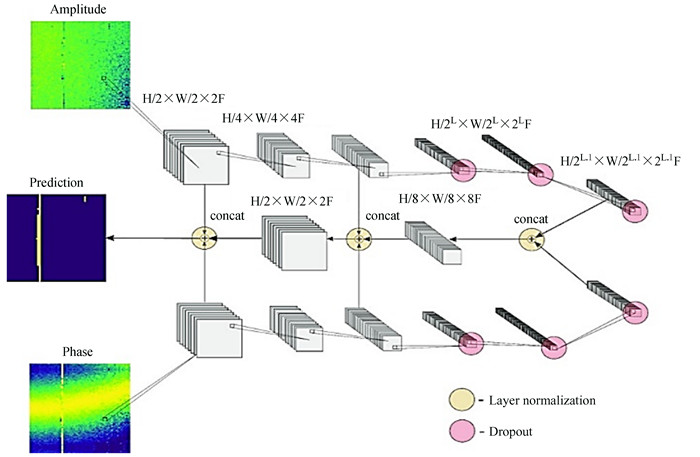
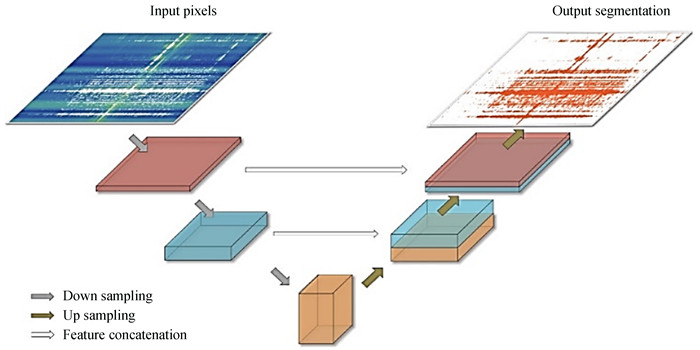
文[28]提出了全卷积神经网络(Deep Fully Convolutional Neural Network, DFCN)用于图像的分割,解决的核心问题是图像像素级别的分类。文[29]利用全卷积神经网络,如图 13,H和W分别对应输入的时间和频率可见性维数,F为滤波器层数,L对应输入和全卷积层之间的层数总和,以振幅和相位为特征,瀑布图进行特征提取,并标出射频干扰。
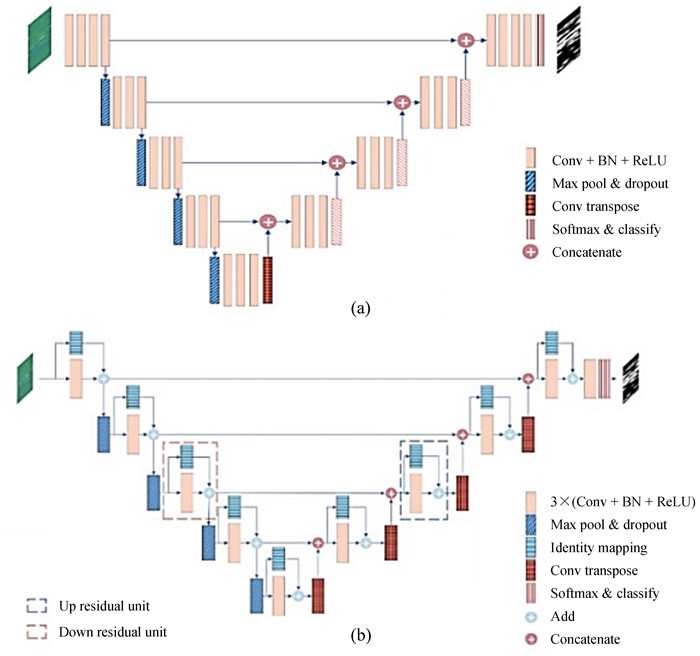
文[30]提出的U-Net神经网络,是在卷积神经网络的基础上增加卷积的扩展路径,可以对小样本的数据集进行较快、有效的图像分割,常用于医学细胞图像分割。文[3]成功应用了U-Net深度神经网络模型来识别单天线射电望远镜数据中的射频干扰,其结构如图 14。
文[5]发现使用卷积神经网络对500 m口径球面射电望远镜数据进行标记射频干扰时,常常标记错误,需要进一步人工检查,带来了显著的额外工作量。为了克服这一问题,文[5]提出了一种称为RFI-Net的神经网络模型,如图 15,结果表明,RFI-Net模型优于U-Net, KNN(K-nearest Neighbour)和SumThreshold算法。
循环神经网络(Recurrent Neural Network, RNN)是一类用于处理序列数据的神经网络,对处理上下文关联的语音[31]数据有很好效果。天文信号也是一种时序数据,非常适合使用循环神经网络对其进行处理,文[32]利用循环神经网络对射电望远镜干涉阵列数据进行射频干扰检测,根据巨型米波射电望远镜(Giant Metrewave Radio Telescope, GMRT)610 MHz的射频干扰振幅信息,区分射频干扰和非射频干扰数据。
5 总结本文系统阐述了射电天文中抑制和标记射频干扰算法和技术,分析了在主动预防阶段、预相关阶段、后相关阶段射频干扰抑制方法的优势和不足。采用有效的屏蔽手段可以在主动预防阶段阻止大部分射频干扰进入系统;预相关阶段基于各个天线中的天文信号具有相关特性抑制射频干扰;在后相关阶段大部分算法基于阈值标记射频干扰。通过机器学习相关技术对射频干扰进行标记和识别是目前的研究热点,基于海量天文数据进行训练能够极大提高标记射频干扰的正确率,但不足是前期手动标记训练样本中射频干扰和天文信号十分耗费时间,目前可用的训练样本有限。
射频干扰抑制问题需要在不同阶段采用多种方法协同解决,从射电望远镜台址周边的无线电环境保护到最终天文数据处理过程各个环节都需要考虑射频干扰问题。各天文台站需要结合实际需求和所处环境的电磁干扰情况,合理选择射频干扰抑制方法。
| [1] | WANG Y, ZHANG H Y, HU H, et al. Satellite RFI mitigation on FAST[J]. Research in Astronomy and Astrophysics, 2021, 21(1): 018. DOI: 10.1088/1674-4527/21/1/18 |
| [2] | PORKO J P G. Radio frequency interference in radio astronomy[D]. Helsinki: Aalto University, 2011. |
| [3] | AKERET J, CHANG C, LUCCHI A, et al. Radio frequency interference mitigation using deep convolutional neural networks[J]. Astronomy and Computing, 2016, 18. |
| [4] |
胡浩, 张海燕, 黄仕杰. FAST电波环境保护措施[J]. 深空探测学报, 2020, 7(2): 152–157 HU H, ZHANG H Y, HUANG S J. Protection measures of FAST radio environment[J]. Journal of Deep Space Exploration, 2020, 7(2): 152–157. |
| [5] | YANG Z, YU C, XIAO J, et al. Deep residual detection of radio frequency interference for FAST[J]. Monthly Notices of the Royal Astronomical Society, 2020, 492(1): 1421–1431. DOI: 10.1093/mnras/stz3521 |
| [6] |
王娜. 新疆奇台110米射电望远镜[J]. 中国科学: 物理学力学天学, 2014, 44(8): 783–794 WANG N. Xinjiang Qitai 110 m radio telescope[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2014, 44(8): 783–794. |
| [7] | 刘晔. QTT台站限制区域电磁干扰影响分析[C]// 中国天文学会2018年学术年会摘要集. 2018: 9-10. LIU Y. Analysis of electromagnetic interference impact in the restricted area of QTT stations[C]// Collection of Abstracts from the 2018 Annual Academic Conference of the Chinese Astronomical Society. 2018: 9-10. |
| [8] |
刘晔, 刘奇. 大口径射电望远镜台址电磁干扰预测方法[J]. 中国科学: 物理学力学天文学, 2019, 49(9): 121–129 LIU Y, LIU Q. A prediction method for electromagnetic interference of large aperture radio telescope[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2019, 49(9): 121–129. |
| [9] | Federal Communications Commission. FCC online table of frequency allocations[R]. Washington: Federal Communications Commission, 2021. |
| [10] | SERIES R A. Preferred frequency bands for radio astronomical measurements in the range 1-3 THz[R]. Geneva: International Telecommunication Union, 2010. |
| [11] | SERIES R A. Protection criteria used for radio astronomical measurements[R]. Geneva: International Telecommunication Union, 2003. |
| [12] | SERIES R A. Characteristics of radio quiet zones[R]. Geneva: International Telecommunication Union, 2021. |
| [13] | CECILIA B, BRADLEY R F. A new approach to interference excision in radio astronomy: real-time adaptive cancellation[J]. The Astronomical Journal, 1998, 116(5): 2598. DOI: 10.1086/300604 |
| [14] | KESTEVEN M, HOBBS G, CLEMENT R, et al. Adaptive filters revisited: radio frequency interference mitigation in pulsar observations[J]. Radio Science, 2005, 40(5): 1–14. |
| [15] | CUROTTO M, FRANCO A. Design, implementation and characterization of a radio frequency interference digital adaptive filter using a field-programmable gate array[D]. de Chile: Universidad de Chile, 2019. |
| [16] | RAZA J, BOONSTRA A J, VAN DER VEEN A J. Spatial filtering of RF interference in radio astronomy[J]. IEEE Signal Processing Letters, 2002, 9(2): 64–67. DOI: 10.1109/97.991140 |
| [17] | HELLBOURG G. Radio frequency interference spatial processing for modern radio telescopes[D]. Orléans: Université d'Orléans, 2014. |
| [18] | KOCZ J, BRIGGS F, REYNOLDS J. Spatial filtering using a multibeam receiver[C]// Proceedings of RFI Mitigation Workshop PoS. 2010, 1: 32. |
| [19] | OFFRINGA A R, DE B A G, BIEHL M, et al. Post-correlation radio frequency interference classification methods[J]. Monthly Notices of the Royal Astronomical Society, 2010, 405(1): 155–167. |
| [20] | OFFRINGA A R. Algorithms for radio interference detection and removal[D]. Groningen: University of Groningen, 2012. |
| [21] | GUO Q, ZHANG C, ZHANG Y, et al. An efficient SVD-based method for image denoising[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2015, 26(5): 868–880. |
| [22] | ADBI H, WILLIAMS L J. Principal component analysis[J]. Wiley Interdisciplinary Reviews: Computational Statistics, 2010, 2(4): 433–459. DOI: 10.1002/wics.101 |
| [23] | KHERIF F, LATYPOVA A. Chapter 12-Principal component analysis[M/OL]. London: Academic Press, 2020: 209-225. https://www.sciencedirect.com/book/9780128157398/machine-learning. |
| [24] | CZECH D, MISHRA A K, INGGS M. Time domain classification of transient radio frequency interference[C]// Proceedings of the IEEE International Geoscience and Remote Sensing Symposium. 2016. |
| [25] | PISNER D A, SCHNYER D M. Chapter 6-Support vector machine[M]// Machine Learning. London: Academic Press, 2020: 101-121. |
| [26] | NAZAR I M, AKSOY M. Radio frequency interference detection in microwave radiometry using support vector machines[J]. URSI Radio Science Letters, 2020, 2: 1–5. |
| [27] | AGGARWAL C C. Neural networks and deep learning[M]. New York: Springer, 2018. |
| [28] | LONG J, SHELHAMER E, DARRELL T. Fully convolutional networks for semantic segmentation[C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2015: 3431-3440. |
| [29] | KERRIGAN J, PLANTE P L, KOHN S, et al. Optimizing sparse RFI prediction using deep learning[J]. Monthly Notices of the Royal Astronomical Society, 2019, 488(2): 2605–2615. |
| [30] | RONNEBERGER O, FISCHER P, BROX T. U-Net: convolutional networks for biomedical image segmentation[C]// Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention. 2015: 234-241. |
| [31] | WANG C, NIEPERT M. State-regularized recurrent neural networks[C]// Proceedings of the International Conference on Machine Learning. 2019: 6596-6606. |
| [32] | BURD P R, MANNHEIM K, MARZ T, et al. Detecting radio frequency interference in radio-antenna arrays with the recurrent neural network algorithm[J]. Astronomische Nachrichten, 2018, 339(5): 358–362. |